中低速磁浮交通低置路基动力特性三维数值分析
2022-11-12李宏泉李金光周苏华
戴 旺,李宏泉,李金光,周苏华
(1. 湖南省交通规划勘察设计院有限公司,湖南 长沙 410082; 2. 湖南大学工程结构损伤诊断湖南省重点实验室,湖南 长沙 410082 )
目前,国内外学者重点关注的是中低速磁浮交通轨道技术、列车技术、高架桥轨道梁结构等[1]。 但对于线路结构的关注较少,尤其是对于介于高架桥和地下隧道之间的低置线路结构的动力反应的研究基本未见,主要是缺乏低置路基的设计和施工方面的实践经验。
丁兆锋[2]研究了中低速磁浮低置结构路基基床动荷载影响深度,基床填料所需的最小变形模量。 周飞[3]分析了填土容重对中低速磁浮基床厚度影响.肖乾等[4]对磁悬浮列车动力学研究进行了详细的综述。单春胜[5]采用Midas 建立了中低速磁悬浮桥梁的有限元分析模型,利用Vimtb 开展了列车-桥梁竖向耦合振动仿真分析。王党雄[6]通过数值模拟揭示了中低速磁浮列车运行时车与轨道梁空间耦合振动特性。 王亚明等[7]则进一步研究了列车-F 轨-钢轨枕-轨道梁系统的动力特性。 受限于计算效率和现有的数值计算理论,目前轨道-路基结构动力响应数值模拟普遍采用半无限平面应变方法进行分析, 而且列车运行动荷载简化为点荷载,这与轨道-路基结构的动力学特性存在较大出入。
长沙磁悬浮连接长沙高铁南站到黄花机场,全长18.225 km,部分区段采用了低置线路,即在填筑路基结构上架设轨道梁。 中低速磁悬浮采用低置路基可以有效降低线下结构自重,对减少差异沉降及工后沉降、维持轨道高平顺性、降低工程造价意义重大。 本文根据长沙磁悬浮列车的实际运行情况,借助Abaqus 和Fortran 联合仿真,建立基于无限元人工边界条件[8-10]的磁悬浮列车-轨道梁-路基-地基三维有限元耦合系统模型, 在Abaqus 中建立了磁浮轨道梁-路基-地基耦合模型, 使用Fortran 建立磁悬浮列车运行荷载Vdload 子程序,将荷载施加到磁浮轨道梁上研究磁悬浮中低速行车状态下低置路基动力特性。
1 耦合系统动力特性分析模型
1.1 轨道梁-路基-地基耦合系统模型
1.1.1 几何分析模型
轨道-路基-地基耦合系统的三维几何模型,模型从上向下分别为轨道梁、垫块、路基、地基土等。为兼顾仿真计算效率和科学性,本文构建的模型的结构尺寸与实际一致,同时对部分工艺和电气结构尺寸进行了简化。 如图1 所示,计算模型的长宽高寸尺分为105,80 m 和50 m。
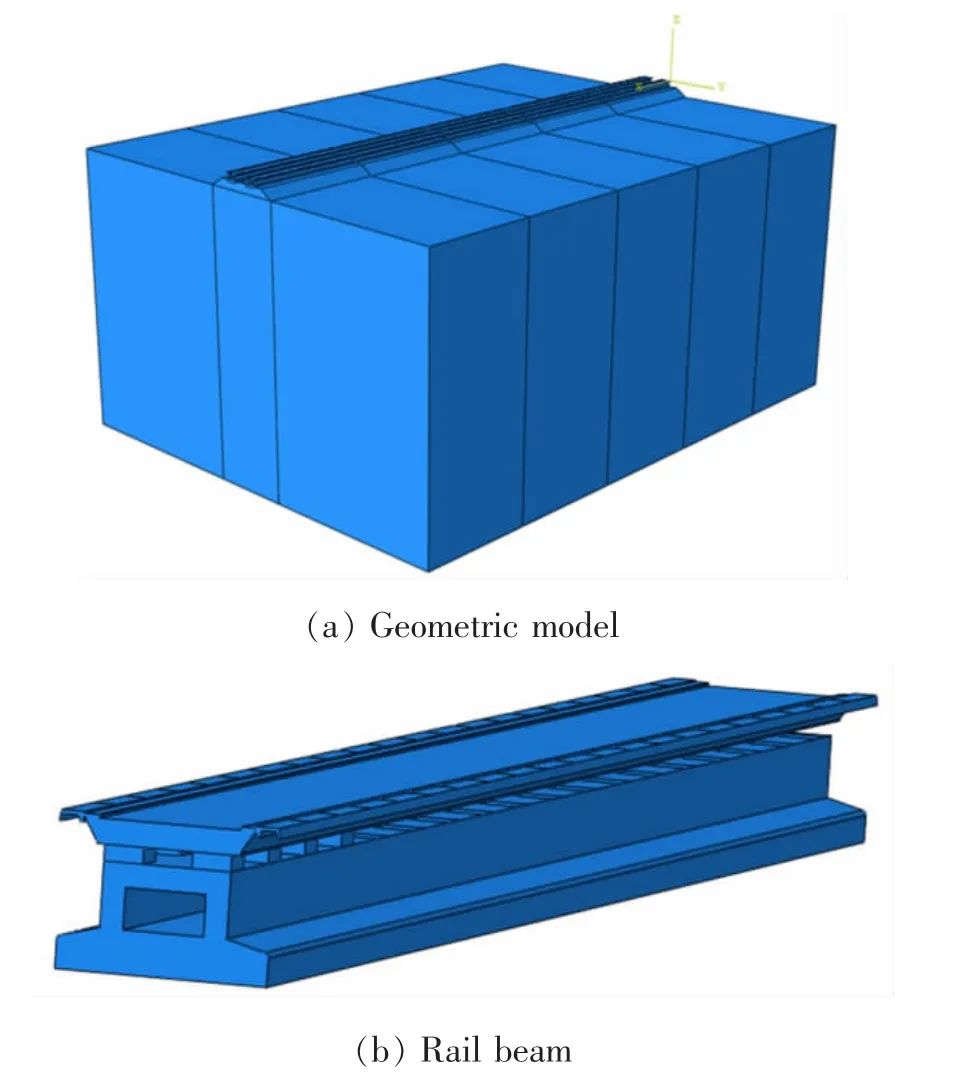
图1 几何分析模型图Fig.1 Geometric Analysis Model
1.1.2 计算参数
在模型分析中,轨道梁、垫块以及路基均假定为弹性体,其中轨道梁和垫块的弹性模量为30 GPa,泊松比为0.17,密度为2 500 kg/m3。 路基的弹性模量为160 MPa,泊松比为0.3,密度为2 400 kg/m3。地基土采用摩尔-库伦模型, 弹性模量为20 MPa,泊松比为0.3,密度为1 800 kg/m3,粘聚力为30 kPa,内摩擦角为20°。为更有效地反映轨道结构、地基土等材料的动力特性,有限元分析模型中采用瑞利阻尼(Rayleigh damping)[11-12],轨道梁和垫块、地基土、路基的质量阻尼Alpha 分别等于0.9,0.85,0.4。
1.1.3 边界条件
采用图1(a)所示的全局坐标系,并规定如下:沿线路方向为X 轴,平面上垂直于路线方向为Y 轴,Z轴垂直于地面。 本研究将模型的四周单元设置为无限元以避免振动波在边界单元处造成的反射。
1.1.4 网格划分
轨道梁、 路基以及周围地基土体划分密集网格,网格尺寸在0.2~0.96 m 之间。 地基其它区域按照离隧道距离网格尺寸逐渐加大,网格尺寸在0.96~4.8 m 之间,网格划分如图2 所示。有限元单元使用C3D6R 单元(6 节点3 棱柱单元),无限单元采用CIN3D8,共划分462 540 个网格单元。

图2 网格划分图Fig.2 Grid segmentation
1.2 计算荷载
采用沿轨道方向钢轨表面内5 个区域的均布荷载来简化代替作用于路基上的移动荷载。 简化后的荷载,每个区域为一段,每段2.72 m,荷载大小为25.8 kN/m。
长沙中低速磁悬浮车辆采用3 节车体组合型式,含梁端挂钩车体总长46.75 m。 轨道梁受荷简图如图3 所示。

图3 轨道梁受荷简图Fig.3 Charged diagram of track beam
对于轨道不平顺引起的动荷载,为简化起见并参照已有的研究[13-14],本文将其简化为一个包含振动幅值和频率的正弦函数形式如下

式中:P0为单个车轮静载,kN;P1为对应于动力附加荷载的振动荷载,kN。m0为列车簧下质量。根据文献[15-17],振动荷载幅值P1=m0aω2,其中a 为波幅,ω为圆频率。对于长沙磁悬浮列车,P0=35 kN,P1=3.68 kN(v=140 km/s),P1=4.8 kN(v=160 km/s),ω=17.5 s-1(v=140 km/s),ω=20 s-1(v=160 km/s)。
此外, 由于Abaqus 没有预置移动荷载的设置程序, 本研究通过Fortran 编写了Vdload 子程序模拟磁悬浮列车运行产生的荷载。
1.3 分析过程
本文分析软件采用Abaqus,模型单元采用6 节点三棱柱的实体。 本文数值模拟研究磁悬浮列车提速至140,160 km/h 情况下,低置路基的动力响应情况, 使用Fortran 编写Vdload 子程序模拟磁悬浮列车运行产生的荷载,本文有限元动力分析采用显示积分算法进行求解[11]。
2 模拟结果及讨论
现有研究表明[5-7],行车荷载作用下路基的动力反应与列车运行速度、 基床刚度和基床阻尼等因素密切相关。本文着重探讨不同列车速度,基床刚度,基床阻尼对低置路基动应力分布和传递规律的影响。
2.1 行车激励下路基动应力研究
线路中心处混凝土垫层下路基动应力Pd随时间t 的变化规律如图4 所示。
由图4 可知,当0.75 s 时,磁悬浮列车正好运行到模型的中心位置。 运行磁悬浮的轨道梁底垫层A 点下不同深处D 处路基的动应力见图5 所示。 由图5 可知,垫层下路基动应力分布不均匀,最大动应力位于轨道梁垫层内侧(右侧轨道,见图5 中A 点),点),向轨道梁垫层外侧逐渐减小,最大、最小动应力相差1.7 kPa。

图4 140 km/h 运行时混凝土垫层下路基动应力随时间的变化规律Fig.4 140 km/h dynamic stress under concrete cushion at any time
调取图5 中A 点以下路基不同深度D 处的动应力,见图6 所示。由图5 可知,A 点以下路基的动应力沿深度逐渐减小,0~0.6 m 减小幅度较大,0.6~1.4 m减小幅度趋缓;磁悬浮列车运行速度140 km/h 引起的路基动应力最大不超过9 kPa。

图5 磁悬浮140 km/h 运行时轨道梁底垫层下不同位置处路基的动应力Fig.5 Stress of subgrade at different positions under the bottom cushion of track beam during operation of magnetic levitation 140 km/h
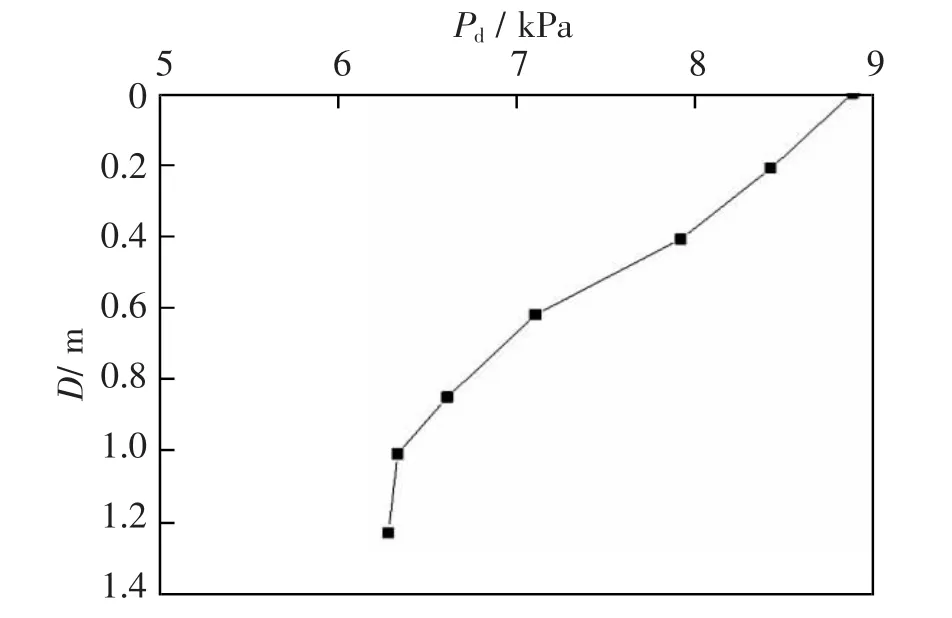
图6 垫层下路基动应力沿深度的分布规律Fig.6 Distribution of stress along depth of subgrade under cushion
同样可以得到磁悬浮列车运行速度为160 km/h时,不同时间点路基动应力云图和160 km/h 运行时混凝土垫层下路基动应力和轨道梁底垫层下不同位置处路基的动应力随时间的变化规律。
2.2 行车速度对路基动应力响应的影响
图7 为不同速度下路基动应力沿深度的分布规律,当列车运行速度为160 km/h 时产生的路基表层动应力为9.2 kPa, 比140 km/h 运行时产生的路基动应力大3.6%;路基0.6 m 以下列车速度对路基动应力基本没有影响。

图7 不同速度下路基动应力沿深度的分布规律Fig.7 Distribution of dynamic stress along depth of subgrade at different velocity
2.3 基床刚度对路基动应力响应的影响
图8 为磁悬浮列车以设计时速140 km/h 运行时, 路基刚度分别取80,120,160 MPa 和200 MPa时不同深度处的路基动应力图。 从图中可以看出,基床刚度越大,路基表层动应力越大,但增加幅度逐渐趋缓, 路基0.6 m 以下动应力随基床刚度的增大而减小。 基床刚度的变化对路基加速度和弹性变形的影响不大。
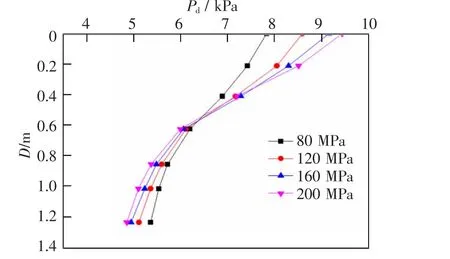
图8 不同基床刚度下路基不同深度处的动应力Fig.8 Distribution law of dynamic stress along depth of subgrade at different velocity
2.4 基床的阻尼对路基动应力响应的影响
图9 为磁悬浮列车以设计时速140 km/h 运行时,路基的瑞利阻尼Alpha 分别取0.75,0.8,0.85 和0.9 时不同深度处路基的动应力分布规律图, 其中瑞利阻尼Alpha 与磁悬浮路基材料的阻尼比及自振频率相关,详见文献[18-20]。

图9 不同基床阻尼下路基不同深度处的动应力Fig.9 Dynamic stress at different depth of subgrade under different bed damping
由图9 可知,基床阻尼对路基表层的动应力没有影响,但对路基下方深处的动应力影响较大。 基床阻尼越大,深度越大的路基动应力越小,动应力的衰减幅度越大。 基床阻尼的变化对路基加速度和弹性变形的影响基本可忽略不计。
3 结论
本文为了考虑中低速磁浮交通在中速行车状态下低置路基的动应力分布和传递规律,建立了基于无限元人工边界条件的磁悬浮轨道梁-路基-地基耦合系统。 探究了不同行车速度,基床刚度,基床阻尼对低置路基动应力分布和传递规律的影响,主要结论如下。
1) 列车车速越大,路基动应力响应越大,不过对0.6 m 以下路基的动应力影响不大。
2) 随着基床刚度的增大,路基表层动应力出现明显的增大, 但增加幅度逐渐趋缓, 但当路基在0.6 m 以下时,动应力随基床刚度的增大而减小。
3) 不同基床阻尼对路基表层的动应力没有影响,但对路基下方深处的动应力影响较大,基床阻尼越大,深度越大的路基动应力越小,动应力的衰减幅度越大。
