轴向冲击下锚固锚杆变形与应力特征分析

2022-11-11司林坡娄金福杨景贺原贵阳

煤炭学报 2022年10期

司林坡，娄金福，杨景贺，原贵阳

(1. 煤炭科学研究总院开采研究分院，北京 100013；2. 中煤科工开采研究院有限公司，北京 100013；3. 煤炭科学研究总院煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

近年来，随着煤矿开采深度的逐渐增加，煤层赋存地质条件逐渐趋于恶劣，给巷道支护带来了一系列挑战[1-2]；冲击地压因其特有的易发、多发、难防治特征，成为影响煤矿生产最为突出的动力灾害之一，冲击地压巷道支护难题最为显著[3]。冲击地压发生常伴随着强烈动载荷，锚杆支护系统在冲击载荷作用下是否能保持稳定是冲击地压巷道安全使用的关键[4-5]，锚杆作为支护系统的主要构件也将承受严重的冲击作用，明晰锚杆在冲击载荷下的力学响应特征具有现实意义。

国内外许多学者采用实验室试验与数值模拟手段针对锚杆和锚杆支护系统在冲击载荷作用下的力学响应特征进行了大量的研究工作。在实验室试验方面，主要通过落锤或爆破对锚杆施加动载荷，St-Pierre和CAI Ming等[6-7]采用落锤试验对锥形锚杆动载响应规律及特征进行研究，得出落锤冲击速度是影响锚杆变形的关键因素，动量是影响冲击载荷作用下锚杆是否破坏的关键指标。LI和DOUCET[8]开展大量的D锚杆落锤试验，得出D锚杆在冲击载荷下的延伸量与冲击能量呈现线性相关关系，D锚杆吸收能量的能力取决于锚杆的断面面积、抗拉强度和延伸率。TANNANT和BRUMMER[9-10]监测了爆破动载下的锚杆应变和围岩质点速度，分析认为爆破动载引起的锚杆震动比围岩震动时间更长，各连接处的阻尼影响应力波的传递。OTUONYE[11]对全长黏结式锚杆在爆破冲击荷载作用下的动力响应特性进行了研究，得出在岩石表面处测量的锚杆振速与峰值应变大于在岩体内部测得的振速与应变，沿锚杆全长各点的轴向振速与频率各不相同的结论。王爱文等[12]利用静-动加载试验系统研究了等强与非等强螺纹钢锚杆在静载和动载条件的力学响应特征，分析了锚杆不同加载条件下的锚杆自由段端部轴力-位移曲线特征和预应力对锚杆变形的影响。IVANOVIC和NEILSON等[13]同样研究了锚杆预应力对锚杆遭受冲击载荷时力学响应的影响。GISLE[14]通过模型试验得出，当爆源距离锚杆3～4 m时，爆破平面应力波对锚杆的支护效果不产生影响。顾金才等[15]研制出岩土工程抗爆结构模型试验装置对不同类型的锚固洞室进行了抗爆模型试验，得出大量关于锚杆(索)在爆破作用下动载力学响应特征的研究成果。付玉凯等[16]采用自由落锤冲击试验装置对不同锚杆进行了侧向抗冲击性能试验，分析了侧向冲击能量对锚杆的动力响应特征的影响。张亮亮等[17]研究了爆炸波作用下，预应力锚索的索端张力变化特征与锚固段轴向应变变化波形。杨苏杭等[18]研究得出在爆炸荷载作用下，锚索与被加固岩体处于强烈的动态共同工作状态，与静载条件下锚索受力单调增加或减少的规律显著不同。在数值模拟研究方面，张玉宝、赵同彬等[19-20]采用Abaqus软件分析了不同冲击能量条件下端锚锚杆的抗冲击力学性能，得到锚杆全过程动力响应特征。杨自有、顾金才等[21]利用LS-DYNA软件模拟了锚杆对围岩的加固效果和动态力学性能，分析硐室围岩在用锚杆加固作用下，由爆炸波引起的岩体垂直应力、围岩变形以及锚杆杆体应变的变化特点，并将结果同模型试验结果进行一致性比对。

众多学者从不同角度对锚杆(索)或锚固结构的动载响应进行了系统研究，所得成果大力推动锚杆支护机理与技术的发展。但支护系统中的锚杆不能仅做材料来进行研究，它是与其他支护构件、锚固剂、围岩组合在一起，在井下存在特定工况，现有研究针对锚杆材料或相似材料力学性能开展的测试工作较多，少数研究针对全尺寸锚杆，但普遍没有考虑井下锚杆实际工况；尤其是关于冲击载荷作用下，支护系统中锚杆不同位置变形、应力分布特征及时序效应的研究成果鲜有报道。笔者将全尺寸锚杆、支护构件、围岩等组合体作为支护单元，利用锚杆力学性能综合试验台对支护单元中的锚杆先进行轴向拉伸，模拟井下承载结构中围岩扩容变形，在预加静载基础上进行冲击测试，模拟井下锚杆在承受高静载作用下发生冲击，研究锚杆不同位置的变形、应力分布及时序特征；采用LS-DYNA数值模拟软件进行仿真计算，与试验结果进行对比验证和分析，从更细观的角度研究井下锚杆在冲击载荷下的力学响应规律。研究成果对揭示锚杆的作用机理和失效过程具有重要价值，可为冲击地压巷道锚杆支护设计提供借鉴与参考。

1 锚杆冲击试验设备及方案

1.1 锚杆轴向冲击试验设备

锚杆力学性能综合试验台及试验方案设计原理与井下锚杆实际受冲击载荷的对应关系如图1所示。

图1 试验系统原理Fig.1 Principle of test system

现场生产实践中，能量以冲击波形式自震源经深部岩体传播至巷道围岩。巷道浅部围岩(不连续岩块)在冲击波作用下向巷道空间内部运动，因不连续岩块与锚杆同向运行的加速度差导致岩块对锚杆托盘产生作用力，托盘受到螺母约束，从而对锚杆产生轴向冲击拉伸载荷。试验台中的摆锤沿锚杆轴向撞击冲击梁砧板，在冲击作用下，冲击梁推动锚杆托盘向外快速移动，由此再现井下冲击地压发生时锚杆支护系统中锚杆的受力与变形过程，冲击梁前端与锚杆托盘之间设置水泥砂浆模型，尽可能保证试验条件与井下实际情况相近。

在内径φ122 mm钢制锚固模型管中注入水泥砂浆，预留直径φ80 mm的孔，将粘贴有应变片的直径φ22 mm锚杆竖直立于钻孔中心，粘有应变片的全尺寸锚杆如图2(a)所示，用CGM-1高性能水泥基灌浆料将锚杆锚固在钻孔中。本次锚杆轴向冲击试验选用煤矿常用的500号普通热轧左旋无纵肋螺纹钢锚杆，为监测冲击载荷作用时间段锚杆不同位置响应情况，沿锚杆不同位置粘贴应变片，采用DH5922D型动态应变仪采集变形响应数据，采用动载传感器和激光位移传感器监测锚杆自由端载荷和位移变化数据，试验材料参数及设备技术参数见表1。

图2 全尺寸锚杆试件Fig.2 Sample of full-size bolt

1.2 锚杆轴向冲击试验方案

为了解锚杆不同位置在轴向冲击载荷作用下变形特征，沿锚杆轴向在锚固段和自由段各布置4个测点，因在测试过程中图2(a)中红色圆圈标识的应变片超量程失效，实际有效测点位置如图2(b)所示。

表1 试验材料参数及设备技术参数

在各测点粘贴型号BE120-3AA、规格(长×宽)3 mm×2 mm、阻值120.5 Ω、灵敏系数2.22的应变片，应变片表面涂防水胶并用纱布包好。

为更加真实模拟井下锚杆在冲击瞬间的受力环境，对杆尾螺母施加350 N·m扭矩，再准静态拉伸至屈服强度80%左右后进行轴向冲击，模拟井下锚杆在高静载条件下遭受冲击。试验采用的500号普通热轧左旋无纵肋螺纹钢锚杆屈服强度约为210 kN，因此，设计准静态拉伸锚杆轴向力为165 kN，拉伸速率为0.3 kN/s。保持油缸载荷，根据试验对冲击能量要求，将摆锤升至预定高度释放撞击冲击梁，从而产生对锚杆杆体的冲击作用，本次试验施加的轴向冲击能量为10 kJ，试件自由段参与冲击响应的实际长度为1 580.8 mm(锚杆总长减去锚固端长度和杆尾至球垫平面的长度)。

2 冲击载荷下锚杆变形过程

2.1 冲击作用下锚杆整体变形过程

图3 轴向冲击载荷下锚杆受力与变形过程Fig.3 Deformation and load process of bolt under axial impact load

试验台为液压加载系统，为消除加载停止后液压系统压力降导致载荷降低的影响，实际加载时适当提升了设定载荷限，导致实际加载数值与设计数值存在一定的出入；实际轴向拉伸结束后，锚杆的初始轴向载荷为171 kN。为便于叙述，将锚杆发生拉伸变形记为正，收缩变形为负。并将摆锤与冲击梁接触前的某一时刻作为计时零点，冲击载荷作用下锚杆自由端载荷和轴向变形过程如图3所示。由图3(a)可知，轴向冲击载荷作用下，锚杆托盘位置载荷从171 kN(实际初始拉伸载荷)瞬时增加至438 kN，此后处于振荡状态，振幅逐渐减小；在12.4 ms左右，端部载荷衰减至初始静载状态后加速减小，在26.3 ms左右，摆锤与撞击梁脱离，锚杆托盘处载荷降为0。图3(b)显示，杆体轴向变形约在12 ms内由12.11 mm(初始静载拉伸变形量)迅速伸长至34.65 mm，伸长22.54 mm；而后收缩至28.39 mm左右，并趋于稳定。由此表明，试验条件下，在10 kJ能量的冲击下，支护单元中的锚杆最终产生28.39 mm塑性拉伸变形。

2.2 锚杆不同位置变形过程

冲击载荷作用下锚杆整体变形是其各部分变形的矢量和，不同位置对冲击载荷的响应程度及先后顺序存在明显差异。为明晰锚杆对轴向冲击载荷响应规律，对锚杆不同位置变形过程进行分析。

如图4所示，当摆锤落下对锚杆进行轴向冲击时，锚杆杆体上布设的所有测点瞬时拉伸后小幅收缩，出现振荡；此后，自由段距离锚固段与自由段分界面较近的5号和6号测点出现再次拉伸现象，达到峰值后快速振荡收缩；其余测点则在应变保持一段相对稳定的阶段后快速收缩，收缩过程中同样存在振荡现象；总体来看，自由段振荡的频率和幅度大于锚固段，锚固段内振荡现象随着锚固深度的加大而减弱。锚杆冲击响应结束后，各应变片处于相对平稳阶段，锚杆产生塑性变形。

图4 轴向冲击载荷下锚杆不同位置变形过程Fig.4 Deformation process of bolt at different positions under axial impact load

为了更清晰的说明各应变片响应情况，分别选取自由段和锚固段内的5号和4号测点进行分析，如图5所示。图5(a)中，由A点至B点为5号应变片瞬时拉伸阶段，在静态拉伸的基础上瞬时拉伸量为1 706×10-6；B点到C点为振荡阶段，此阶段应变增量为120×10-6；C点到D点为再次拉伸阶段，此阶段应变增量为1 139×10-6；D点到E点为收缩阶段，冲击梁与锚杆托盘脱离，此阶段应变变化量为3 346×10-6；E点以后为应变相对稳定阶段，该处产生的塑性变形量为1 923×10-6。图5(b)中由A′点至B′点为4号应变片瞬时拉伸阶段，在静态拉伸的基础上瞬时拉伸量为1 375×10-6；B′点到C′点为相对稳定阶段；C′点到D′点为收缩阶段，此阶段应变变化量为2 937×10-6；D′点以后为应变相对稳定阶段，该处产生的塑性变形量为286×10-6。各应变片在不同阶段的应变变化量见表2。以锚杆自由段端部为起始点，将测点准静态拉伸和冲击拉伸量总和作为累计拉伸量，将冲击后的测点的瞬时拉伸、振荡拉伸和再次拉伸量的总和作为冲击拉伸量，将累计变形量与塑性变形量的差值作为收缩量，各测点处的应变响应情况如图6所示。

综合图3、图6和表2可以得到，在实验条件下，锚杆遭受轴向冲击后，自由端和锚固段内的测点随着距离锚固段和自由段分界面越近，锚杆拉伸变形量越大，由于锚固的轴向约束作用使得锚固段内杆体的累计拉伸量和冲击拉伸变形量小于自由段，锚杆产生的塑性变形大部分在距离锚固段和自由段分界面相对较近的位置，绝大部分塑性变形量产生在自由段，且距离分界面越近，塑性变形量越大。文献[22]研究指出，应力波在传导介质属性发生变化的界面发生复杂的反射与透射，且产生于原入射波不同类型的新波形。锚杆受到冲击作用后，产生沿杆体轴向传播的纵波，当纵波入射至自由段与锚固段交界面时，不仅反射和透射纵波，同时产生横波，甚至产生交界面波；多种波形耦合作用形成复杂的应力波传播状态是导致上述现象产生的主要原因；此外，应力波的传递方式和反射作用导致锚杆的拉伸和收缩均不是稳定完成，存在振荡现象，距离分界面越近，振荡现象越明显；由于锚固的约束和对应力波的吸收作用，锚固段塑性变形量普遍较小，且随锚固深度增加，杆体受冲击影响越小，振荡越不明显。

图5 应变片典型响应过程Fig.5 Response process of gauge

表2 各应变片不同阶段响应情况

图6 各测点应变变化情况Fig.6 Strain change at measuring points

由此可以得出，锚固作用可以使锚杆与围岩较好的耦合，一方面可使冲击产生的弹性波在锚固段内通过杆体透射到围岩体中，充分调动围岩自身的吸能特性；另一方面可降低锚杆的振动幅度，从而减小锚杆振荡变形对锚固界面和围岩造成的破坏，有效防止锚杆脱黏。建议在冲击地压巷道支护采用加长锚固或全长锚固，可提高冲击发生时杆体能量向围岩转移的能力，减小对锚固界面的损伤，使锚杆具有相对更好的锚固基础，从而提高对冲击地压巷道围岩的控制效果。

2.3 锚杆不同位置变形时序特征

轴向冲击载荷作用下，锚杆杆体不同位置发生的拉伸和收缩变形不仅在响应程度方面存在差异，而且在响应时序方面也存在差异。为探究锚杆在轴向冲击载荷下拉伸变形时序特征，对0～1.5 ms时间段内锚杆锚固段及自由段各测点对冲击载荷响应情况进行分析；为了便于更清晰的对比各部位的响应特征，统一将各应变片静态拉伸量对应减去，考察各应变片在瞬时拉伸时的轴向应变增量，数据处理结果如图7所示。

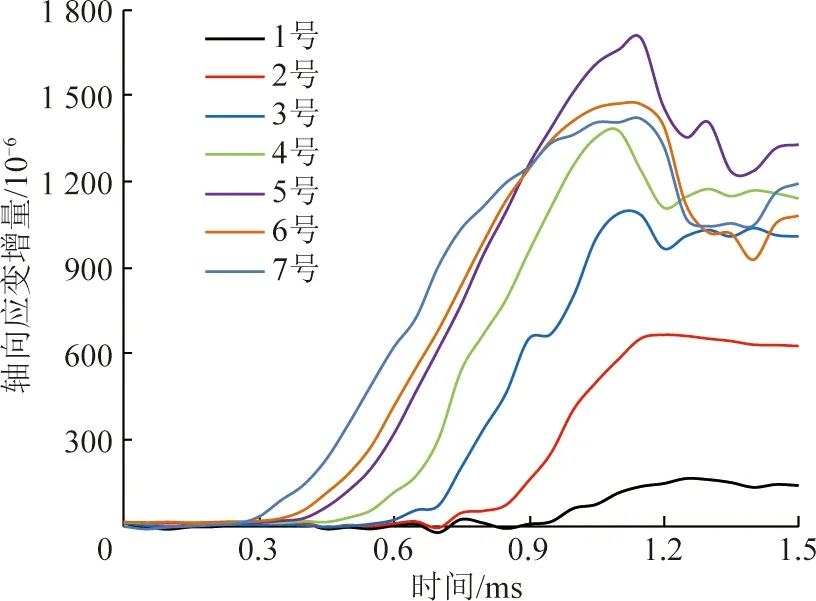
图7 锚杆不同位置拉伸响应时-序特征Fig.7 Time series characteristics of bolt at different positions under axial impact load

由图7可知，自由段内的7号测点在0.30 ms时刻开始发生拉伸变形，最先响应；6号位置测点在0.35 ms时刻发生拉伸变形；5号位置处测点在0.40 ms时响应。锚固段内，距离锚固段与自由段分界面位置由近到远不同位置的应变片响应时间分别为0.50，0.60，0.75和0.95 ms，锚杆瞬时拉伸变形自锚杆尾部向锚固端头依次响应。其原因为摆锤下落冲击位置位于锚杆尾部托盘附近，产生的冲击波自尾部向锚固端头传播，导致拉伸变形自锚杆尾部向锚固端头逐渐响应。由图2可知，7号、6号与5号测点之间的间隔距离均为200 mm，响应时间间隔均为0.05 ms；锚固段内4号测点到1号测点各测点之间的间隔距离分别为225，300和400 mm，相应响应间隔时间分别为0.10，0.15和0.20 ms，响应时间间隔与测点距离间隔正相关。

为了探讨锚杆在收缩阶段的响应时序特征，将锚杆在快速收缩时的时刻进行标识和记录，如图8所示。因锚固深度最大的1号应变片受冲击载荷影响非常小，观察不到明显的快速收缩现象。将2～7号应变片应变快速下降时间点分别标识为J2～J7。通过采集到的数据可得到所对应的时间点分别为13.10，12.15，11.55，11.05，10.75和10.45 ms；时间间隔分别为0.95，0.6，0.5，0.3和0.3 ms。冲击后的收缩变形同样表现为自锚杆尾部向锚固端头逐渐响应，且响应时间间隔越来越大。

图8 锚杆不同位置收缩响应时-序特征Fig.8 Time series characteristics of bolt at different positions under axial impact load

3 数值模拟分析

利用LS-DYNA有限元数值模拟软件对试验方案进行仿真计算，采用Solidworks建模软件对真实数值模型进行构建，采用Hyper mesh对数值模型进行网格划分及边界约束生成K文件，将K文件导入LS-DYNA进行数值计算，采用Hyper view对计算结果进行后处理。

3.1 数值模型几何特征及材料参数

数值模拟方案中，金属材料本构模型为Piecewise Linear Plasticity模型，岩石及锚固剂均设置为Johnson Holmquist Concrete模型，冲击体为边长300 mm、厚度为30 mm的方形刚体，质量设置为200 kg，本构模型为Rigid。为了有效模拟锚杆拉拔过程中的力学工况，杆体采用实体单元建模，横肋角度35°，肋高1 mm，肋间距为10 mm。杆体数值模型材料参数见表3，构建数值模型如图9所示。

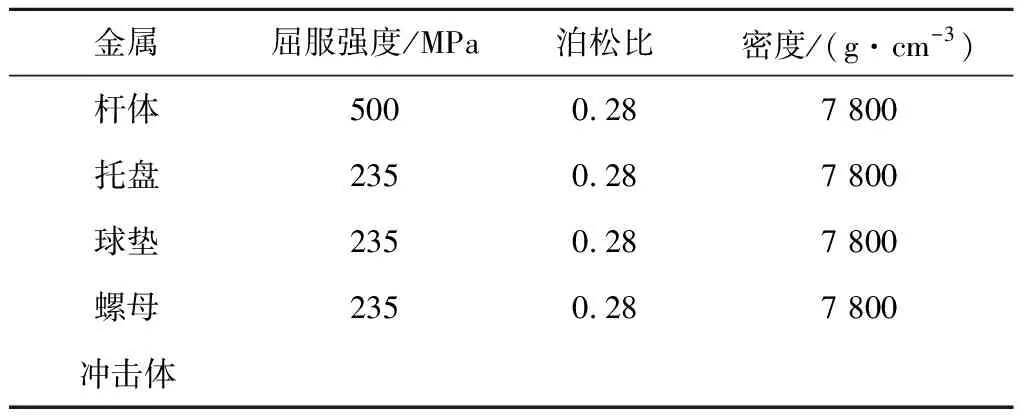
表3 金属材料参数

图9 锚固结构数值模型Fig.9 Numerical model of anchorage system

在接触参数设置方面，将杆体与螺母之间设置为固定接触，锚杆托盘与冲击体连接方式设置为AUTOMATIC_SURF_TO_SURF，杆体与锚固剂之间设置20 MPa的黏结力，用于模拟锚杆杆体与锚固剂之间的黏结作用，锚固剂与围岩之间的黏结力设置为30 MPa[17]。在模型边界条件及加载方案方面，将围岩表面进行固定约束，在锚杆托盘位置处对锚杆先施加165 kN的拉伸力，静力计算时间为50 ms。在静力计算完成后基础上，赋予冲击体10 m/s的速度，使冲击体沿锚杆轴向运动撞击托盘，产生10 kJ的冲击能量，并通过托盘、螺母等构件将冲击能量传递于锚杆杆体及锚固段中。加载路径和方式与实验室试验近似相同，动力计算时间为40 ms。

3.2 锚杆不同位置变形特征

支护单元在轴向拉伸及冲击作用下的等效应力云图如图10所示，为了便于分析，模型中只显示杆体应力云图。锚杆在静力拉伸作用下，最大应力值为425 MPa(50 ms)，处于弹性变形阶段。在施加10 kJ的冲击能量时，杆体自由段内应力值瞬时升高，自由段杆体进入屈服阶段，表明冲击载荷作用下杆体自由段发生了大量的塑性变形，与实验室试验结果基本吻合。

图10 杆体等效应力云图Fig.10 Equivalent stress of bolt

为了分析锚杆在冲击作用下杆体不同位置应变分布规律，从50 ms时刻施加冲击载荷开始，分别以5 ms为间隔提取杆体的应变变化过程如图11所示。

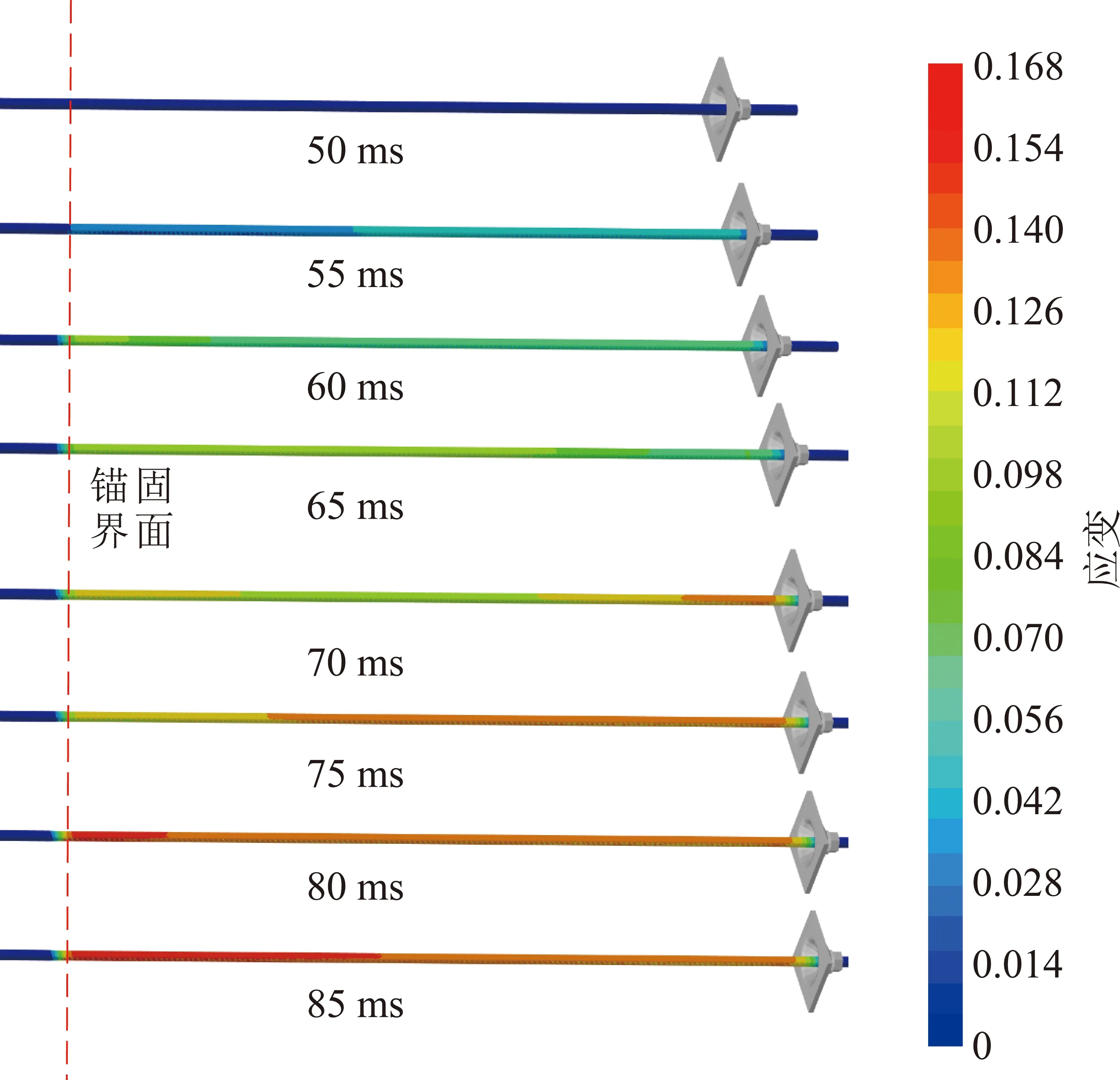
图11 冲击过程杆体应变云图Fig.11 Bolt body strain during impact

通过图11可以看出，杆体在冲击载荷作用下最先在冲击位置产生了塑性变形，随着冲击时间的增加，应变逐渐向锚固段方向传递，当达到锚固界面时，在向锚固深部小范围传播的同时转向自由段大规模反弹。锚固段内，由于应变传递过程中受到黏结力以及横肋咬合作用的影响，使得锚固段内应变传播幅度及范围较小，大部分应变由锚固界面开始向自由段反弹，最终在锚固界面附近形成塑性变形应变最大值，且沿自由段杆尾方向逐渐减小，与实验室试验结果有较好的一致性。

3.3 锚杆不同位置应力特征

为了得到锚杆在冲击载荷作用下不同位置应力变化趋势，按照试验时应变片监测位置，提取7个测点的应力-时间变化曲线如图12所示。

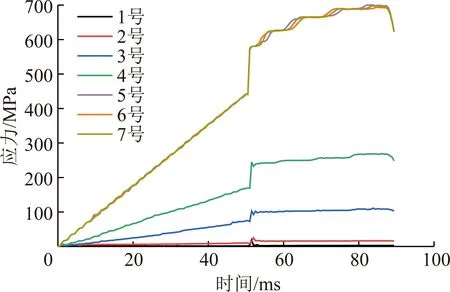
图12 锚杆杆体应力-时间曲线Fig.12 Stress-time curves of bolt body

0～50 ms计算时间之内，锚杆主要承受165 kN的轴向拉伸载荷，自由段内测点(5号、6号和7号测点)应力变化无明显差异，锚固段内测点应力上升幅度低于自由段，且随着锚固深度的增加，应力上升速度及幅度均有明显的降低。计算时间50 ms时刻对支护单元施加了10 kJ的冲击能量，在冲击瞬间，各个测点应力值均产生了明显的升高，与静载变形阶类似，自由段内杆体应力升高幅度明显高于锚固段；锚固段内应力升高幅度随着锚固深度的增加而大幅降低。为了进一步分析冲击时刻应力变化特征，以冲击时刻为应力零点，得到了杆体不同位置的应力增量-时间曲线如图13所示。

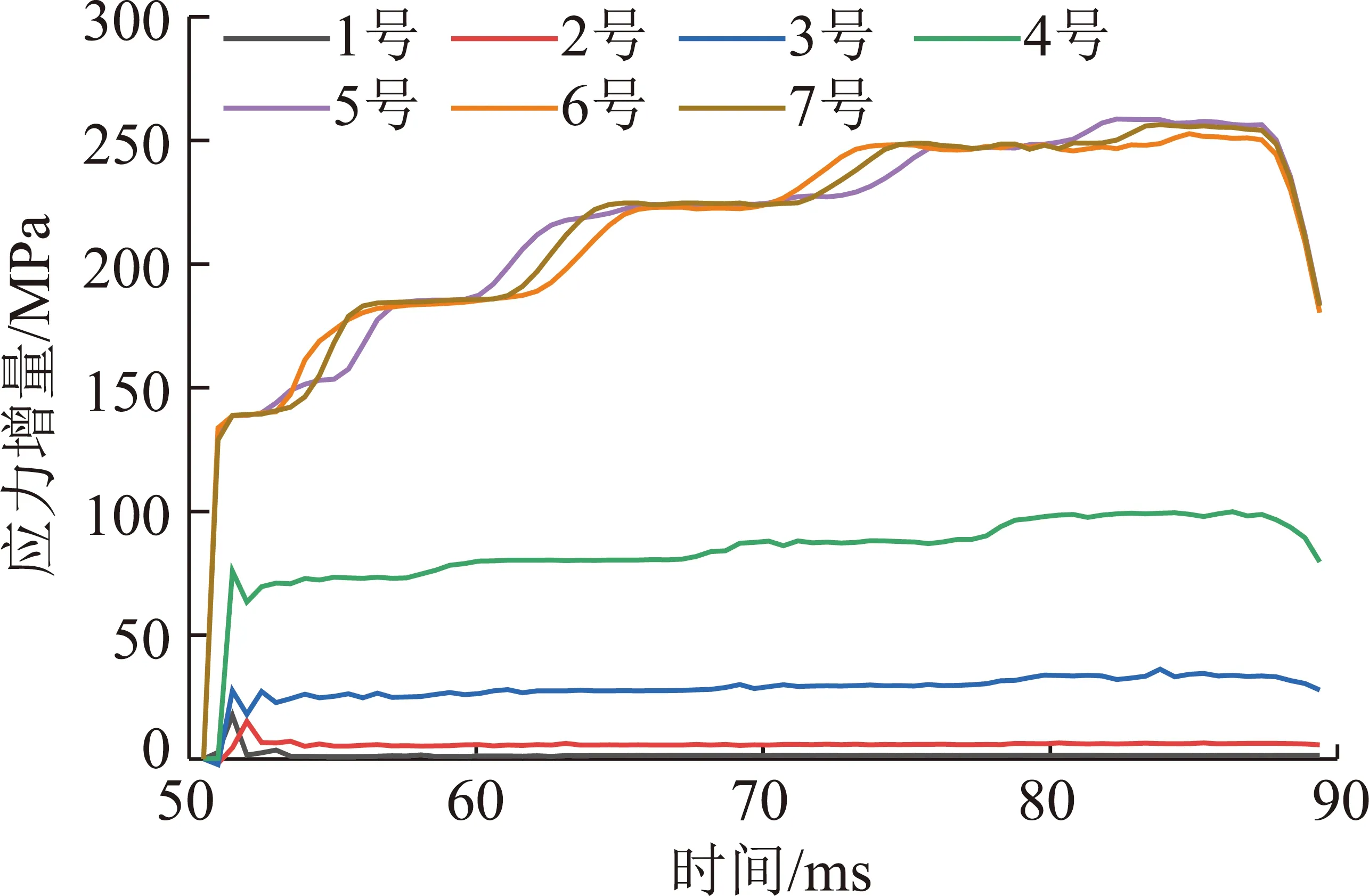
图13 锚杆杆体应力增量-时间曲线Fig.13 Stress increment-time curves of bolt body

综合图12,13所示结果可得，随着冲击能量的施加，各个测点的应力值均产生了瞬间的增加，但是不同位置的测点应力升高幅度及时序响应特征存在较为明显的差异。在自由段内，5号、6号和7号测点受到冲击载荷作用下应力瞬间升高，此后以波动形态逐渐交替增加；锚固段浅部测点比深部测点具有更高的应力升高幅度及速率，表明锚固剂与杆体之间的黏结作用与横肋咬合作用可有效吸收冲击波，减小锚固段内的杆体受冲击载荷的影响。以上应力分布和变化特征与本节及试验室实测应变变化规律(图7)基本吻合。