各向异性初始地应力软岩中自膨胀锚杆扩体-拉拔试验研究

刘 杰，孙荣琪，张 研，宋 瑞，王 昊，孙 涛

(1.三峡大学 三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.湖北省地质灾害防治工程技术中心，湖北 宜昌 443002；3.桂林理工大学 土木与建筑工程学院，广西 桂林 541004；4.桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004)

目前，锚杆已成为矿山、隧道、边坡和水利工程的重要加固结构。 锚杆用于加固岩土时，可有效提高岩土的稳定性[1]。但由于设计不足、围岩围压、锚固应力损失等原因[2]，锚杆可能发生断裂，锚杆与锚固体界面发生滑动破坏，锚固体与围岩界面发生滑动(脱黏)破坏[3]。

锚杆结构在失稳状态下的承载能力称为锚杆的极限抗拔力，是锚固工程设计中的核心技术参数。如何有效提高极限抗拔力是锚杆技术研究的重点之一[4]。早期的试验研究表明，影响锚杆极限抗拔力的主要因素是锚杆的形状[5]、水泥浆的注浆技术和注浆锚固体的性能[6]。近年来，一方面对锚杆结构的创新设计进行了研究。除工程中常用的膨胀壳锚杆外，水力膨胀锚杆和充气锚杆不使用注浆材料，而是通过锚杆体对围岩进行膨胀，并以接触面的摩擦力作为锚杆的承载能力[7]。还有研究在锚杆体上设置翼型结构或负泊松比材料，以增加锚杆体的轴向延性，形成适合软岩大变形的吸能锚杆[8]。

另一方面，近年来，锚固体新材料、新工艺的研究取得了不少成果。例如，用聚合物锚固体代替传统的水泥浆锚固体，可以具有较高的初始强度和承载力[9]，并能适应高性能岩石、高围压和潮湿环境[10]。传统的水泥基锚固材料也可以通过添加辅助材料来具有更好的施工性能[11]。添加适量的粉煤灰和水玻璃后，黏接性能得到了很大的改善。HE等[12]在水泥基锚固材料中添加纤维材料可以提高锚固体的抗拉和抗剪强度。

膨胀剂作为混凝土添加剂，水化反应后可产生巨大的体积膨胀，在约束条件下产生较大的膨胀应力。在岩石静力爆破和混凝土收缩补偿领域得到了广泛应用[13]。近年来，膨胀剂也被应用于岩土加固领域。ZHANG等[14]在超细硅酸盐水泥中加入膨胀剂，结合预应力锚杆注浆加固破碎岩体。XU等[15]提出了以氧化钙膨胀剂为膨胀源的SSAB多点摩擦锚杆，锚固长度为40 cm时最大拉力为235 kN。刘杰等[16]研究发现，以氧化钙和硫铝酸钙为膨胀源的HCSA膨胀剂能较好地促进普通硅酸盐水泥灌浆材料的水化反应，缩短初凝时间，锚固体需要在侧限足够的条件下具有良好的长期稳定性。但膨胀剂在锚杆结构中的应用也应充分考虑岩土体强度参数、变形参数和围压的影响。其中，围压作用下锚杆一般采用应力各向同性厚壁圆筒模型[17-18]，仍存在一定局限性。

笔者提出了一种在水泥基材料中掺入较大比例HCSA的自膨胀锚杆。介绍了锚固材料和机理。基于各向异性的初始应力场，推导了自膨胀锚杆扩孔膨胀变形的解析解。通过钢管模型试验，研究了不同刚度围岩中自膨胀锚杆的膨胀变形演化规律。通过数值模拟得到了锚杆极限上拔力的上拔规律。最后，提出了基于软岩参数和围压影响的HCSA掺量设计方法。

1 自膨胀锚杆锚固机理

本研究围绕的自膨胀锚固材料主要成分为普通硅酸盐水泥、HCSA、水和其他添加剂。HCSA的主要成分为：80%CaO、12%高铝水泥、8%石膏。其反应产物主要是Ca(OH)2和3CaO·Al2O3·3CaSO4·32H2O(钙矾石)。CaO变为Ca(OH)2过程体积膨胀率约为2[19]，钙矾石形成过程中的体积膨胀率约为1.32。本研究所使用的HCSA经测定，其体积自由膨胀率为2.238。

在刚度较大介质(如硬岩)中，自膨胀锚固材料的HCSA掺量建议不超过30%，掺入适量的HCSA可使内部充分挤密，微小空泡闭合，进而提升锚固体密实度。若HCSA掺量过高，岩石会因为较大的径向膨胀应力而发生拉伸破坏，进而影响锚固系统稳定性[21]。

自膨胀锚杆抗拔力的提升因素主要分为如下3部分：① 提升浆液密实度；② 提升锚固体-围岩、锚固体-锚杆杆体界面摩擦力；③ 自膨胀形成锚固体扩大头。

但对于刚度较低、易变形的介质(例如软岩、土体)，自膨胀锚杆的锚固力提升主要因素还不确定。即岩土介质在较大膨胀应力作用下扩孔特征明显，局部扩孔可增加锚杆拉拔阻力；但由于自膨胀锚固体的自扩头效应，其内部膨胀应力会一定程度释放，从而影响摩擦力提升的效果。

另一方面，考虑到一般软岩的强度较低特性，在较大膨胀应力作用下往往易破碎。但作者认为，软岩周边若存在一定的初始地应力场形成约束，限制其变形，应该能提高其承载能力。因此，本文首先基于现实情况的各向异性初始地应力场建立自膨胀锚杆的扩孔数学模型并展开物理模型试验。

2 各向异性初始地应力中自膨胀锚杆膨胀变形解析解

2.1 基本力学假设

锚杆受围岩影响时大多采用厚壁圆筒模型计算。该模型能描述重力方向与锚杆轴向平行时的锚固结构受力情况，即围岩初始应力各向同性。但工程实际中，如深埋隧道、高陡边坡和深基坑中的近乎水平向锚杆体系所受围岩初始应力为各向异性，厚壁圆筒模型不再适用。

笔者参照刘杰等[20]推导的初始应力各向异性的锚杆周边围岩应力解，假设围岩是均质且各向同性的弹塑性体，并暂时假定自膨胀锚固体均匀膨胀，挤压围岩时膨胀应力q维持恒定，进行如下推导。

2.2 推导过程

在满足以上假定情况下，根据自膨胀锚杆体系受力特点，可将受力模型简化为平面应变问题，忽略平行于沿锚杆轴向膨胀应力、初始应力的影响。因此，锚杆开始注浆阶段的应力解为

(1)

当锚固体初凝后，一方面产生了膨胀应力q；另一方面认为锚固体力学参数与围岩相近，锚孔被锚杆、锚固体填充，r=0，锚孔边界从小孔应力集中问题变为实体接触问题。将膨胀应力q和新边界条件代入式(1)得

(2)

平面应变问题中物理方程为

(3)

式中，ερ为径向应变；εθ为周向应变；γρθ为剪应变；E为弹性模量；μ为泊松比。

极坐标下的几何方程：

(4)

式中，uρ为径向变形；uθ为周向变形。

联立式(2)～(4)，可得锚固体周边围岩径向变形：

(5)

式中，f(θ)为积分后的余量，是关于θ的任意函数；g(ρ) 为积分后的余量，是关于ρ的任意函数。

联立式(3)～(5)，得

(6)

联立式(5)和(6)可解出f(θ)，g(ρ)，并代入式(5)得

(7)

其中，C，D，F为常数。当孔径r无限小，锚固体与围岩接触面的径向变形可忽略不计，即r→0，且ρ=r时，uρ=0。将边界条件代入式(7)，要使θ取任何值时等式都成立，需满足系数C=D=0。同理，当围岩无初始应力时，即B=0，uρ=0。将边界条件代入式(7)，可得要使等式成立，需满足系数F=0。因此，此问题的弹性位移解为

(8)

自膨胀锚杆周边围岩径向刚度KR可表示为

(9)

令ρ=r时，得围岩与锚固体接触面上的径向刚度一般式为

(10)

由式(10)可知，锚杆围岩接触面径向刚度KR随θ而改变，具有明显的各向异性特点。KR还受径向膨胀应力q的影响，具体表现为q越大，则KR越大。

邓亮等[18]通过厚壁圆筒模型推导得到等效径向刚度表达式为

(11)

对比式(10)，(11),将px=py=0，代入式(10)，可得与式 (11)一致的结果。

3 同介质不同刚度中自膨胀锚杆的模型试验研究

3.1 试验过程

试验采用不同壁厚无缝钢管模拟不同刚度的围岩。其中，钢管长度400 mm，钢管内径均为78 mm，壁厚分为8 mm(A组)，5 mm(B组)，3 mm(C组)三种。试验图如图1,2所示。图1中的内置锚杆杆体为φ28 mm玻璃纤维锚杆，钢管上下端封堵材料为速凝水泥砂浆，灰砂质量比1∶1，水灰质量比1∶0.6，速凝剂掺量5%。

图1 不同壁厚钢管Fig.1 Different wall thickness steel pipe

图2 应力监测Fig.2 Stress monitoring

灌浆材料的膨胀剂掺量ζ按照10%，15%，20%，25%配比，具体的材料配比见表1，并测得了不同配比时的浆液自由膨胀率。

浇筑完成后，通过压力传感器实时监测装置的径向应力，并每隔2 h使用游标卡尺测量钢管中部管径3次取均值。若不计膨胀过程中钢管壁厚t的变化，测量的变形量即为锚固体的膨胀量。

3.2 试验结果分析

试验的径向应力和变形监测在72 h内逐渐稳定，径向膨胀应力-应变曲线如图3(a)所示。

表1 自膨胀锚固体灌浆材料配比

图3 t=3，5，8 mm不同ζ应力-应变增长曲线Fig.3 Stress-strain growth curves of different ζ at t=3，5，8 mm

3.2.1 膨胀过程的径向应力应变演化规律

由图3可知，壁厚越薄，应变越大，应力越小。膨胀剂掺量10%时，不同壁厚钢管中的径向应力应变关系均接近线性，即自膨胀锚固体的变形模量是常数。而膨胀剂掺量大于10%的试验组，钢管中的径向变形模量随壁厚增加呈不同的速率增长，具体表现为：壁厚越大、膨胀剂掺量越高，变形模量增速越快。

3.2.2 膨胀过程的应变能演化规律

通过图3并结合式(12)计算接触面的应变能密度U，得到如图4所示结果。

(12)

图4 应变能密度与钢管壁厚关系曲线Fig.4 Relationship curves between strain energy density and steel pipe wall thickness

已知膨胀剂掺量相同时，锚固体的膨胀总能量一定。由图4可知，在膨胀剂掺量大于10%时，膨胀应变能密度随壁厚增加而降低。其中应变能密度降低率最大为55.1%，即壁厚更大的钢管能更好地约束锚固体的膨胀变形，减少应变能耗散。

3.2.3 稳定时的径向应力-变形规律

根据图3绘制稳定后的应力-变形图(图5)。由图5可知，若保持膨胀剂掺量不变，增大钢管壁厚时，应力增大、变形减小的变化过程可看作较均匀的平移；若保持钢管壁厚不变，提升膨胀剂掺量，应力增大、变形增大的变化过程也近似平移，但其速率表现出“慢—快—慢”的规律。这是由于当膨胀剂较低时(ζ≤15)，有较大比例的膨胀能消耗在了锚固体内部挤密过程中，因此呈现出了径向应力随膨胀剂掺量的非线性增长关系。

图5 稳定时的应力与变形关系Fig.5 Relationship between stress and deformation at stability

总之，在钢管内径一定时，膨胀剂掺量和壁厚共同决定了锚固结构稳定时的应力、变形水平。

因此，引入膨胀剂掺量ζ和钢管壁厚t，可得关于中间变量ζ,t的径向应力σρ、径向变形uρ表达式为

(13)

f(t)=4.595t-42.24

对范围内的ζ，t赋值，即可获取不同膨胀剂掺量、钢管壁厚的径向应力与变形量。

上述钢管模拟围岩，可通过监测的径向应力、径向变形求取体系膨胀过程的等效径向刚度KR1～KR3。假设岩石泊松比μ均为0.23，计算25%HCSA时的等效径向变形模量E1～E3。

代入式(11)计算出的E1～E3可表征以下岩体[21]，见表2。

表2 钢管模拟围岩表征参数

4 不同刚度介质中自膨胀锚杆加固数值模拟

基于第3节的试验参数，采用ABAQUS数值模拟软件，进行自膨胀锚固体扩张-拉拔模拟，验证第2节理论公式可靠性，并比较在不同刚度介质中的自膨胀应力-变形对锚杆极限抗拔力提升效应。

4.1 自膨胀锚固体扩张变形模拟

自膨锚杆的扩张变形模拟及拉拔模拟均采用三维有限单元模型，为提高计算效率，拉拔模拟中采用以锚杆中轴为中心将锚固结构分割成4份，取1份作为研究对象，如图6所示。其中模型具体参数为：锚杆杆体直径28 mm，锚杆杆体长5.25 m，自膨胀锚固段长1 m，自由段长4 m。材料弹性模量Eb=200 GPa，μb=0.25，密度ρb=7.89 g/cm3。锚孔直径与钢管模拟的孔径一致为78 mm。围岩为3 m×3 m×10 m各向同性均匀介质。

图6 锚杆拉拔模型网格划分Fig.6 Meshing of bolt drawing model

锚固体参数不考虑自身的密实度增强效果，与围岩参数相同，取表2结果，泊松比μ同为0.23，密度ρ同为2.3 g/cm3。在锚固体上施加均匀向外膨胀的应力q，其取值与图6中25%HCSA结果一致。

对图7(a)中模型的前、后、右、下4个面施加法向固定约束。从模型顶面和左面施加初始应力px和py，初始应力根据BROWN[22]总结地应力的水平主应力与竖直主应力比的经验关系进行取值，px=13.524 MPa，py=11.27 MPa，并从锚固体向外施加膨胀应力q。对锚杆杆体施加0.1 mm/s的拉拔荷载。锚杆-锚固体、锚固体-围岩接触面设置黏结接触，锚杆-锚固体界面摩擦固数为0.5，锚固体-围岩接触面摩擦因数为0.1。网格采用三维应力单元，共划分69 030 个C3D8I单元。

经计算，获取不同刚度介质中的锚孔自膨胀扩张应力-变形分布规律如图7所示。

图7 围岩-锚固体接触面径向应力、径向变形、周向应力分布Fig.7 Circumferential stress distribution diagram，deformation distribution map，stress distribution diagram of surrounding rock-anchor solid contact surface

4.1.1 径向应力分布规律

由图7(a)可知，围岩-锚固体接触面径向应力仿真结果与式(2)计算结果较为相近。接触面径向应力σρ在各个角度方向上均为受压状态，且其数值受初始应力px，py，膨胀应力q以及围岩径向刚度KR三重影响。其中，θ为90°和270°的最大应力区是σρ最大的区域。

4.1.2 径向变形分布规律

由图7(b)可知，围岩-锚固体接触面径向变形仿真结果与式(8)计算结果较为相近。在非均匀初始应力场作用下，HCSA掺量从0增至25%，接触面径向变形从负值变为正值，即锚孔由收缩转为扩张。且y方向初始地应力小，扩孔变形更显著，扩孔形状近似椭圆。

4.1.3 周向应力分布规律

由图7(c)可知，围岩-锚固体接触面周向应力σθ受KR影响较小，受初始应力px，py以及膨胀应力q影响较大。且随着HCSA含量增加，σθ明显从压应力转向拉应力。其中，围岩初始应力更大的x方向周向拉应力更显著。

4.1.4 初始应力作用下的自膨胀应力-变形规律

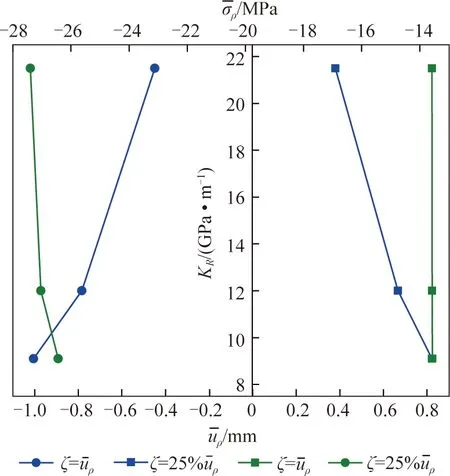
图关系曲线

HCSA25%时，随着刚度从K3到K1，即约束减小，平均径向应力降低约3.6%，而图6中采用钢管模拟时，径向应力降低8.6%。这说明，当围岩刚度较弱时，围压的存在可减少自膨胀锚固体径向应力的耗散。而平均径向变形增大约117%，有明显的的扩体效应。为此，本文探讨范围内的KR，对uρ的影响较对σρ的影响更明显。

4.2 自膨胀锚杆拉拔模拟

通过数值模拟计算出ζ=0和ζ=25%时自膨胀锚杆在刚度为K1～K3的围岩中的拉拔荷载位移曲线，如图9所示，并将相关特征汇总到表3中。

图9 荷载位移曲线Fig.9 Load-displacement curves

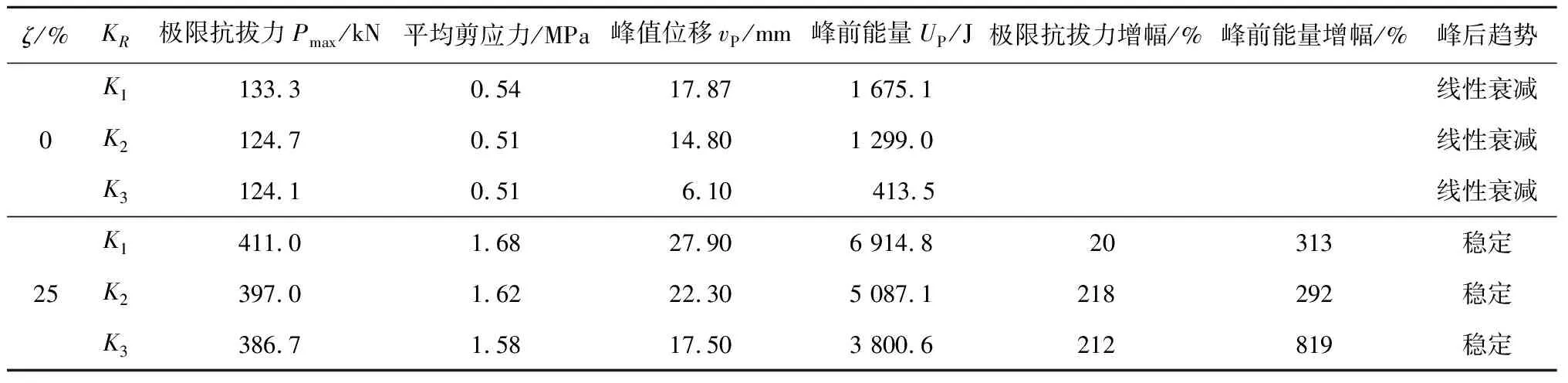
表3 拉拔结果特征

由图9和表3可知，相比ζ=0，ζ=25%时，不同KR的锚杆极限抗拔力增幅相近，平均在210%。径向应力σρ和径向变形uρ适中的K2围岩中锚杆极限抗拔力增幅最大，且库伦摩擦力相较于扩体效应对锚杆极限抗拔力的贡献更大。

若不考虑岩性差异，在初始应力作用下，ζ=25%时自膨胀锚杆锚固体-围岩界面平均剪应力增大约44%。即初始应力对自膨胀锚杆的单位长度锚固力有较大影响。

从能量而言，KR越大vP越小，进而使得UP随vP减小。但ζ=25%时，K3的峰前能量增幅达到819%，这是由于自膨胀锚杆材料能明显增加锚杆的峰前位移vP，提高锚杆正常工作时的安全储备。

另一方面，相比ζ=0，25%时的锚杆脱黏后的滑移阶段荷载均保持稳定，未发生衰减，有良好的脱黏后吸能效果。

4.3 建立自膨胀锚固结构控裂设计方法

笔者采用无缝钢管模拟自膨胀锚杆作用下的锚固结构变形过程，围岩参数只考虑了径向刚度KR。但事实上，软岩自身较低的抗拉强度T和黏聚力c等参数决定了其并不能承受较大的径向膨胀应力q，q一旦超过软岩承受范围即发生起裂，进而降低锚固结构的承载能力。刘杰等[20]提出了一种基于原位浅孔胀裂试验的自膨胀锚杆膨胀剂掺量设计方法，但在地下工程中进行的胀裂试验会产生安全隐患。因此，还需根据软岩抗拉强度T和黏聚力c等参数确定容许的膨胀剂最大掺量ζ，即建立自膨胀锚固结构的控裂设计方法。

由图7(a),(c)中的应力分布可知，最大应力区围岩中有最大径向压应力和最大周向拉应力。因此，将最大应力区的锚固体-围岩作为研究对象。假设沿锚杆轴向的应力为中间主应力，以压应力为正绘制出摩尔应力圆，如图10所示。

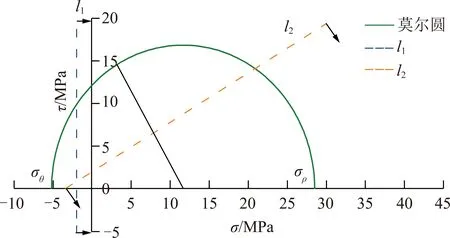
图10 最大应力区的单元体莫尔圆Fig.10 Mohr circle of the element body in the maximum stress zone

图10中，l1为围岩抗拉强度T临界线，l2为围岩剪切破坏包络线。图10中ζ=25%时的莫尔圆与l1和l2相交，说明围岩已开裂。因此，要保证围岩不开裂，需同时满足以下条件：

(14)

将式(2)代入式(14)，并令θ=π/2，整理得

(15)

已知在无初始应力时，由式(2)得σρ=q，将式(13)代入式(15)可得

(16)

其中，在已知KR时，f(t)为常量。因此，已知围岩初始应力px和py、抗拉强度T、内摩擦角φ和黏聚力c时，可计算出自膨胀锚固体中容许掺入的膨胀剂最大掺量ζmax。同时，当围岩参数已知，若初始应力px和py越大，则膨胀剂最大掺量ζmax越大。

4.4 自膨胀锚固结构控裂设计方法验证实例

为验证本文建立的以软弱围岩强度参数和初始应力等为判据的膨胀剂掺量设计公式是否能应用于工程实践，进行了如下试验研究。

4.4.1 试验方案

试验选取三峡库区某废弃矿山边坡，坡高7 m，坡角76°，在坡底钻取4个直径为78 mm、孔深为1.25 m 的孔洞，每个孔洞之间相距2 m，钻孔和岩心如图11所示。

图11 现场钻孔和岩心Fig.11 On-site drilling and core

选取4根直径28 mm长度1.8 m的钢筋锚杆，锚固长度1 m，在距离锚杆底部500 mm处布置薄膜应力传感器。按表1配制4组膨胀剂掺量为5%，10%，15%和20%的膨胀水泥浆，对应孔号分别为A，B，C，D。

记录各时段的膨胀应力以及对应孔洞的胀裂情况。在浇筑完成10～15 h后，锚固体-围岩破坏情况如图12所示。

图12 不同ζ锚固体-围岩破坏情况Fig.12 Different ζ anchor solids-failure of surrounding rock

由图12可知，ζ=10%，ζ=15%的锚固体-围岩未出现裂缝，ζ=20%锚固体被胀裂，围岩出现细小裂缝。ζ=25%锚固体-围岩均出现大裂缝导致锚固失效。

4.4.2 围岩力学参数的测定(取样法)

现场取回的岩心一部分切割成高度100 mm、直径50 mm的圆柱形试样。保证每个钻孔所取岩芯能够制备3个试样，共计4组12个岩样。对试样进行三轴压缩试验，如图13所示。

图13 三轴压缩试验Fig.13 Triaxial compression test

控制每组3个试样围压分别为2，4，6 MPa，进行抗压强度试验，获得相应的应力应变曲线，求出对应的弹性模量E和泊松比μ，通过绘制其莫尔应力圆的包络线，可得出岩样的黏聚力c和内摩擦角φ。

另一部分岩芯制备成高度50 mm，直径50 mm的圆柱形试样，对试样进行劈裂试验，如图14所示。每组3个平行试验取平均值，得到4组岩心对应的抗拉强度。以所取岩芯的抗拉强度表征钻孔围岩抗拉强度。

图14 岩样劈裂试验Fig.14 Rock sample splitting test

剩余岩心用排水法测定原位岩石的容重γ，根据刘杰等[20]提出的围岩原位初始应力计算公式，且本文所选边坡已解除构造应力，可得到px和py计算值。试验结果见表4。

4.4.3 测定锚固材料膨胀应力

因材料具有膨胀性，故采用自主研发的适用于自膨胀介质的制样装置，如图15所示，并在模具内壁布置薄膜应力传感器。按表1分别配置ζ为10%，15%，20%，25%的锚固体灌浆材料，并对膨胀应力进行监测，具体数值如图16所示。

4.4.4 围岩胀裂破坏试验分析

通过图16得到在ζ不同的条件下自膨胀锚固灌浆材料的膨胀应力，结合表4围岩参数。将相应数值代入式(15)中，其中ζ=20%，ζ=25%不满足。因此，在使用本文提出的自膨胀锚固灌浆材料对该试验所选取的矿山边坡进行锚固时，在ζ=20%，ζ=25%条件下会发生锚固体-围岩开裂。

表4 岩石基础试验数据统计

图15 自膨胀锚固材料制样装置及膨胀压力监测Fig.15 Self-expanding anchor material sample preparation device and expansion pressure monitoring

图16 不同ζ条件下膨胀压力-时间变化曲线Fig.16 Expansion pressure-time curves under different ζ conditions

膨胀剂掺量设计公式计算结果与图12所示试验结果一致，说明该公式在判断ζ不同的条件下锚固体-围岩是否开裂已具有一定的可行性。

5 结 论

(1)自膨胀锚杆是一种黏结式端部扩大头锚杆。它利用膨胀剂在约束条件下产生的正应力，增大锚固体结构的密实度和接触面摩擦力，并形成端部扩大头。达到增加锚固结构承载力的目的。

(2)基于工程实际的各向异性初始地应力场，推导了自膨胀锚杆与围岩接触面的径向应力、径向变形和径向刚度解析式，并通过数值模拟方法验证了解析式的可行性。同时，根据上述结果和围岩自身参数建立了自膨胀锚固结构的控裂设计方法并推导了膨胀剂掺量设计公式，对三峡库区某废弃矿山边坡进行试验，验证了该公式的可行性。

(3)根据钢管试验结果，建立了以钢管壁厚和膨胀剂掺量为变量的径向膨胀应力-变形关系式。在降低钢管壁厚时，不同ζ对应的应力-变形的变化趋势高度一致。其中，在ζ较大时，降低钢管壁厚径向膨胀应力仅减小8.6%，但径向变形量却增大117%，说明扩大头效应更明显。

(4)锚杆拉拔数值模拟显示，相比素水泥黏结锚杆，ζ=25%的自膨胀锚杆对锚杆极限抗拔力和峰前位移均有较大提升。在不同刚度的围岩中极限抗拔力提升幅度均接近210%，但自膨胀锚杆在相对较高的围岩中抗拔力峰前能量增幅明显更大，达到819%。说明摩擦力对自膨胀锚杆锚固性能的影响比扩体效应更优。