基于蚁狮优化算法的直流变换器分数阶PIλDμ控制

肖海飞，曾国辉，杜 涛，黄 勃，刘 瑾

(上海工程技术大学 电子电气工程学院，上海 201620)

直流变换器具有电气隔离、电压变换以及能量传输等功能，被广泛应用于固态变压器[1](Solid-State Transformer，SST)、分布式发电和电动汽车等领域中。在实际应用中，直流变换器需要具有良好的动态性能和鲁棒性能，而在直流变换器中采用分数阶PID(Fractional Order PID，FOPID)[2]控制，可以有效提高其性能。

近年来，智能算法逐步被应用到分数阶PID控制器的参数整定中以优化其控制器参数。文献[3]采用量子粒子群方法对分数阶PID控制器参数进行整定，且选取高低温试验箱作为被控对象进行实验研究。实验结果表明在该优化方法下，系统的性能得到了提高。文献[4]提出将图像法和人工鱼群优化算法相结合的方法来对分数阶PIλ控制器进行参数整定。该研究通过仿真验证了采用人工鱼群算法得到的控制器动态特性更优，并且提高了系统的动态性能指标。文献[5]从Buck变换器数学模型出发，分析了不同积分阶次λ对系统稳定性的影响，确定了分数阶控制器的参数。文献[6]将分数阶PID控制应用到移相全桥ZVZCS变换器中，使用遗传算法分别优化分数阶PID 控制器与整数阶PID控制器。仿真结果表明，遗传算法优化分数阶PID控制器下的移相全桥ZVZCS变换器具有更好的动态性能。但是，在将智能算法应用到分数阶PID控制中时，由于一些智能算法[7-8]全局搜索能力不够强，收敛速度较慢，算法寻优能力也不足，导致直流变换器优化的效果不佳。

蚁狮优化[9](Ant Lion Optimization，ALO)算法是一种自然启发式算法，其本质上是一种群体智能算法。与传统的粒子群优化(Particle Swarm Optimization，PSO)算法、蚁群优化(Ant Clony Optimization，ACO)算法、蝙蝠算法(Bat Algorithm，BA)等相比，ALO算法不易陷入局部最优解且搜索精度高，收敛速度较快[10]。将ALO算法应用于分数阶PI参数整定，能快速精准地确定控制器参数。本文提出了一种采用蚁狮优化算法改进双有源桥[11](Dual Active Bridge，DAB)型直流变换器分数阶PIλDμ控制器的方法[12]。本文采用蚁狮优化算法对分数阶PIλDμ控制器进行参数优化，从而提高直流变换器输出电压的响应速度和稳定性，并将该方法与传统工程经验整定整数阶PID、粒子群算法[13]整定分数阶PIλDμ的变换器进行了对比分析。

1 DAB变换器建模

DAB全桥型直流变换器原、副两边各有一个H全桥电路，其中间由1个高频隔离变压器连接，拓扑结构如图1所示。

图1 DAB变换器电路拓扑

图1中，V1和V2分别为原、副两边全桥的电压，Co1和Co2分别为两侧直流滤波电容，L是串联电感，up为原边全桥的交流端电压，us为经变压器折算到副边的电压。

图2为DAB移相控制工作原理波形。根据原边和副边瞬时功率相等的原理，忽略损耗，对电流i1和i2在静态工作点附近施加扰动并进行线性化，最终得到DAB的小信号模型[14]

图2 DAB移相控制工作原理波形图

(1)

(2)

在式(1)和式(2)中，令

(3)

(4)

(5)

式(3)～式(5)中的变量与式(1)和式(2)中的变量解释对应相同，DAB的等效小信号电路如图3所示。

图3 DAB变换器小信号模型

根据图3可以得到输出电压关于输入电压扰动和占空比扰动的传递函数Gvu和Gvd，其中Co2为副边电感。

(6)

(7)

2 分数阶PIλDμ控制器设计

2.1 分数阶微积分

分数阶控制策略是从数学领域的分数阶微积分理论发展而来的。分数阶微积分有多种定义，文中采用分数阶微积分的Grunwald-Letnikov定义[15]

(8)

2.2 分数阶PIλDμ控制器的数字实现

分数阶PIλDμ控制器的传递函数为

(9)

式中，Kp、Ki和Kd分别是比例、积分和微分系数；sλ和sμ是分数阶微积分算子；阶次λ和μ取值范围通常为0～1。当λ=1且μ=1时，式(9)即为传统的整数阶PID控制器。分数阶PIλDμ控制器增加的参数λ和μ提高了系统的可调性和响应性能[12]。

在将分数阶系统应用在工程的控制系统中时，需要对其进行近似化处理。Oustaloup滤波算法[16]是最为常用的一种近似算法。本文中，拟合频率段为(ωb，ωh)，滤波器阶次取N，Oustaloup滤波器为

(10)

式(10)中，有

(11)

(12)

(13)

式中，α为积分阶次。

3 ALO优化DAB变换器分数阶PID控制器的实现

3.1 蚁狮优化算法及其建模

群智能算法大多从各类生物上获取灵感，蚁狮优化算法也不例外，其主要仿生蚁狮猎捕蚂蚁的行为。蚁狮会提前在沙子中埋下一个圆锥形的深坑，等待蚂蚁落入陷阱。蚂蚁落入陷阱后，蚁狮会把捕获的蚂蚁拉入沙坑下面吃掉，随后扔出残骸并重新挖坑构筑陷阱，为下次狩猎准备。

在模拟蚂蚁随机移动寻找食物时，需令蚂蚁随机移动，蚂蚁随机行走计算式为

Xt=[0，cumsum(2r(t1)-1)，cumsum(2r(t2)-1)，…，

cumsum(2r(tT)-1)]

(14)

式中，cumsum代表蚂蚁随机移动位置信息进行计算后的累加和；t和T分别代表当前迭代次数和最大迭代次数；r(t)代表随机函数

(15)

式中，rand生成[0，1]内均匀分布的随机数。

在ALO算法优化过程中，MA为蚂蚁位置矩阵，ML为蚁狮位置矩阵。将蚂蚁的适应度值放在OA矩阵中，OL为蚁狮适应度值矩阵，OA和OL分别如式(16)和式(17)所示

(16)

(17)

式中，n和m分别为蚂蚁和蚁狮的数量；d是维数，蚂蚁的数量和蚁狮的数量保持一致。

通过式(18)对蚂蚁的位置更新进行规范化处理，使其保持在一定范围内

(18)

(19)

(20)

蚁狮的适应度代表蚁狮建立凹坑陷阱的大小，高适应度的蚁狮代表着更深、更容易捕获蚂蚁的陷阱。在该算法中，可以自适应地减小落入凹坑的蚂蚁随机移动的超球面半径，计算式为

(21)

(22)

式中，t为当前迭代次数；T为最大迭代次数；ω是基于当前迭代定义的常数[9]。当t=0～0.1T时，ω取1；当t=0.1T～0.5T时，ω取2；当t=0.5T～0.75T时，ω取3；当t=0.75T～0.9T时，ω取4；当t=0.9T～0.95T时，ω取5；当t=0.95T～1T时，ω取6。

蚁狮捕食完蚂蚁后，蚁狮的位置更新计算式为

(23)

ALO算法每次迭代都会根据适应度值选择一只蚁狮保存为精英蚁狮，精英蚁狮的存在将影响每次迭代时蚂蚁的移动。另一个影响蚂蚁移动的是轮赌盘选择的蚁狮。蚂蚁朝着精英蚁狮和轮赌盘选出的蚁狮移动，对应的蚂蚁移动计算式为

(24)

3.2 基于ALO算法的分数阶PIλDμ控制器设计

采用Oustaloup滤波法在Simulink中建立分数阶PID控制器仿真模块，然后基于ALO算法对式(6)和式(7)的DAB变换器传递函数进行参数整定。在算法目标函数构建中，选择时间乘以误差的绝对值广积分的ITAE指标[17]，并考虑系统的动态响应速度和抗干扰能力。以系统的ITAE指标作为相应的适应度函数，如式(25)所示。经过参数寻优，得到相关的控制器参数Kp、Ki、Kd、λ和μ。将得到的控制器参数值应用到具体的DAB变换器分数阶PIλDμ控制器中即可完成参数整定。控制器结构如图4所示。

图4 基于蚁狮优化算法的分数阶PIλDμ控制系统

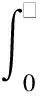
(25)

根据设计的控制系统，在MATLAB/Simulink中进行模型搭建，如图5所示。模型中的传函即为式(7)的DAB变换器输出电压关于占空比的传递函数。

图5 以ITAE为指标的Simulink参数整定模型

3.3 ALO算法整定分数阶PIλDμ控制器的具体步骤

采用蚁狮优化算法整定分数阶PIλDμ控制器参数时，首先对蚁狮个体依次赋值为Kp、Ki、Kd、λ和μ；接着初始化算法基本参数；当确立目标函数，将DAB直流变换器系统性能最优问题等价转化为目标适应度函数，并取得全局最小值Jmin；最后运行算法，得出的目标函数取Jmin时对应的蚁狮个体值，即为待整定的控制器参数值。采用蚁狮优化算法优化DAB直流变换器分数阶PIλDμ控制器的算法流程[18]如图6所示。

图6 算法流程

具体的步骤如下：

步骤1初始化ALO算法。蚁狮和蚂蚁的种群规模为N，算法迭代次数为T，变量维度为d，变量上下限即为算法搜索范围；

步骤2确立目标适应度函数J，将DAB直流变换器系统性能最优问题等价转化为目标适应度函数，并取得全局最小值Jmin；

步骤3初始化蚂蚁和蚁狮的初始位置，通过计算适应度函数获得蚁狮和蚂蚁的适应度值，然后存储最优个体的位置信息和适应度值；

步骤4采用轮赌盘选择蚁狮。蚂蚁围绕着轮赌盘选出的蚁狮和初代精英蚁狮进行移动，蚂蚁和蚁狮的位置按照式(14)～式(24)进行更新；

步骤5蚁狮利用制造的陷阱捕获蚂蚁之后，根据精英蚁狮更新规则，对比适应度值，更新精英蚁狮的位置；

步骤6返回步骤4，进行下一次迭代更新，直至达到设置的最大迭代次数；

步骤7输出的最优蚁狮个体所处的空间位置即为待优化的分数阶PIλDμ控制器参数，算法结束。

4 仿真结果及分析

为了验证基于蚁狮优化算法的分数阶PIλDμ控制策略的效果，将采用MATLAB/Simulink搭建的DAB型直流变换器主电路模型及其分数阶PIλDμ控制电路模型作为实验对象，对比分析传统工程经验整定整数阶PID、粒子群算法整定分数阶PIλDμ控制(PSOFOPID)和蚁狮优化算法整定分数阶PIλDμ控制(ALOFOPID)对DAB直流变换器输出电压性能的影响。DAB变换器的电路参数如表1所示。

表1 变换器参数

本仿真实验中，蚁狮和粒子群种群规模均为N=20，最大迭代次数T=100，待求变量的维度d=5。相应的算法适应度函数收敛曲线如图7所示。

图7 蚁狮优化算法适应度函数收敛曲线

从图7中PSOFOPID和ALOFOPID两种算法适应度函数的迭代收敛曲线中可以看出，与粒子群算法相比，蚁狮优化算法整定的控制器参数寻优在迭代50次左右后，适应度函数值收敛；在最后的搜索过程中，ALOFOPI搜寻到的目标函数值最小。

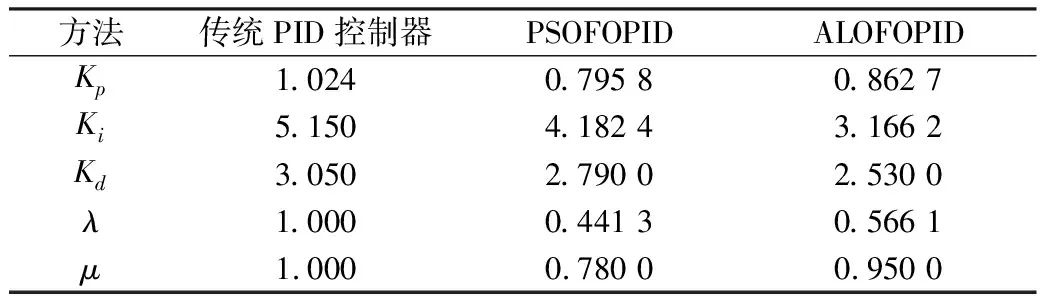
表2 不同方法整定的控制器参数

图8为3种参数整定方法下DAB变换器输出电压波形图对比。由图可知，两次仿真实验均在0.1 s时使负载由128 Ω突变为100 Ω。

图8 3种参数整定方法DAB输出电压对比图

从图8的仿真结果对比中可以明显看出，对于DAB变换器输出电压来说，采用智能算法优化后的分数阶PIλDμ控制器可获得更好的控制性能，而蚁狮优化算法在分数阶PIλDμ控制器参数整定中的优化效果也更好。

不同控制策略下DAB变换器的性能指标对比如表3所示。由表3可知，相较于传统PID控制，智能算法整定分数阶PIλDμ控制器控制下的变换器输出电压超调量和调节时间都有明显提升，上升时间亦有提高；相较于传统PSO算法，ALO算法的优化效果也有一定程度的提升，其系统的超调量和调节时间均有所减少。当负载从128 Ω突变为100 Ω时，ALO算法优化的分数阶PIλDμ控制的DAB变换器输出电压跌落最小，恢复时间最短，且恢复后的电压稳定无振荡。

表3 变换器输出电压仿真性能指标对比

5 实验结果及分析

为进一步验证本文所提采用蚁狮优化算法优化直流变换器分数阶PIλDμ控制器的方法的可行性和有效性，本文基于TMS320F28335型DSP控制器搭建了DAB 变换器实验样机，样机参数如表4所示。

表4 样机参数

图9为采用传统的经验整定PID控制器参数后的DAB变换器输出电压实验波形图。图10为采用粒子群算法整定分数阶PIλDμ控制器参数后的DAB变换器输出电压实验波形图。图11为采用蚁狮优化算法整定分数阶PIλDμ控制器参数后的DAB变换器输出电压实验波形图。表5为3种方法下实物电压性能指标对比。

图9 传统PID控制器

图10 粒子群算法整定分数阶PID控制器

图11 蚁狮优化算法整定分数阶PID控制器

从图9～图11的实验波形可以看到，采用智能算法优化后的分数阶PIλDμ控制器相较于传统PID控制器有着更好的控制性能，DAB变换器的响应速度和负载突变时的电压稳定性更好。表5的性能指标数据也反映了这一点。采用蚁狮优化算法整定分数阶PIλDμ控制器有着最优的控制性能，可以提高DAB变换器动态响应速度，减少超调量，缩短调节时间，并且在负载突变时可降低输出电压波动，提升抗干扰能力。上述结果表明，采用蚁狮优化算法整定分数阶PIλDμ控制器更适合于直流变换器的实际工程应用。

表5 变换器输出电压性能指标对比

6 结束语

在对提高直流变换器的输出电压性能的研究中，本文将智能算法与分数阶PID控制相结合，提出了一种采用蚁狮优化算法改进分数阶PIλDμ控制器的方法。本文基于蚁狮优化算法对分数阶PIλDμ控制器进行参数优化，通过仿真和实验验证了采用该方法的DAB变换器的输出电压拥有更好的动态性能与抗干扰能力。本文研究也为后续将直流变换器与智能控制进一步结合奠定了基础。