一种高性能RLWE加密处理器的设计与实现

王春华，李 斌，杜高明，李桢旻

(合肥工业大学 微电子设计研究所，安徽 合肥 230601)

量子计算机面世后，RSA密码系统[1]和椭圆曲线密码系统(Elliptic Curve Cryptography，ECC)[2]不再安全。环上带错学习(Ring Learning With Error，RLWE)是后量子时代格密码系统中最有潜力的候选方法之一。RLWE问题可以归结为理想格上最坏情况的问题，目前没有已知的量子算法可以有效地解决该问题[3]。由于其自身的安全性及易实现性，RLWE公钥加密系统在云计算[4]、5G通信[5]、数据聚合[6]、签名方案[7]、个人健康数据管理[8]、加密数据上训练神经网络[9]等众多应用中有着广阔的应用前景。

近几年来，RLWE加密方案在软件和硬件方面都得到了广泛研究。文献[10]提出了RLWE公钥加密系统的软件实现。文献[11]在ARM NEON和MSP430架构上实现了RLWE加密方案。文献[12]提出了基于RLWE密码方案的高安全等级的指纹认证系统。

多项式乘法是RLWE公钥加密系统中最关键、最耗时的操作之一。采用数论变换(Number Theoretic Transform，NTT)可以加速多项式乘法。文献[13]提出了一个高效可扩展的RLWE加密微码架构。文献[14]提出了高效紧凑的RLWE加密处理器，该架构将NTT算法和“负折叠”卷积结合，避免了“负折叠”卷积的预计算。文献[15]设计了通用模块化单元，并提出了资源高效且能抵抗侧信道攻击的RLWE加密处理器。但是该架构加解密的吞吐率较低，分别为0.056 Mbit·s-1和0.28 Mbit·s-1。文献[3]提出了高吞吐率的RLWE加密硬件架构，该架构采用基2、基8多路径延迟NTT算法。其加密和解密的吞吐率分别达到每秒兆比特和每秒千兆比特的级别。

上述硬件实现中，文献[14]采用顺序处理的方式执行RLWE加密和解密，该方法占用的硬件资源较少，但是加解密的周期较长且吞吐率低。文献[3]中NTT采用基8算法，该架构加密解密的吞吐率高，达到兆和千兆级别。但是该方法消耗了大量硬件资源，不适合在资源受限的FPGA开发板上实现。本文提出了一个完整的基于RLWE加密处理器硬件架构。该架构在面积和吞吐率上做了折中，在保证高吞吐率的前提下，降低了硬件资源消耗。本文主要研究内容如下：(1)在加密过程中采用NTT运算与密文计算并行处理，同时在NTT以及INTT运算的处理过程中，将数据的读写过程及计算过程进行乒乓操作，隐藏数据的读写周期，降低RLWE加密处理器的延迟，提高了高硬件架构的吞吐率；(2)设计资源复用的硬件架构，加密及解密过程复用蝶形模块中的乘法器和加法器，INTT复用NTT的电路结构，存储模块复用同一块控制电路，从而降低了RLWE加密处理器硬件资源消耗，提高了资源效率；(3)本文设计了中等安全等级(n=256，q=65 537)的RLWE加密处理器，并在Spartan-6 FPGA开发平台上完成了电路实现和硬件测试。测试结果表明RLWE加密处理器加密周期数仅为2 440，解密周期数仅为1 732，吞吐率达到21.01 Mbit·s-1和29.60 Mbit·s-1，证明RLWE加密处理器的性能得到了提升。

本文首先回顾了RLWE加密方案及多项式乘法算法，然后对RLWE加密处理器设计做了详细的介绍，并提出了RLWE加密处理器的硬件架构。最后，本文在FPGA平台上进行了功能仿真及综合实现，并将本文所提架构与现有设计做了对比分析。

1 理论背景

本文对一些符号进行了定义，并对理论背景、RLWE加密方案及RLWE相关算法进行简要介绍。

1.1 基本定义及符号说明

假设多项式项数n为2的方幂，定义R=Z[x]/f(x)为分圆多项式环，其中，f(x)=xn+1。对于正整数q，定义集合Zq=Z/q，Z∈{0，1，…，q-1}，使用符号xmodq表示x落在集合Zq中。本文的向量均采用黑色斜体表示，使用log表示以2为底的对数，⊙表示点乘。

1.2 多项式乘法

RLWE方案主要包括多项式乘法运算和多项式加法运算。多项式乘法是RLWE加密方案最耗时的操作之一。多项式乘法技术主要包括Schoolbook、Karatsuba和NTT算法。算法时间复杂度分别为O(n2)、O(nlog3)和O(n·logn·loglogn)。由于NTT算法时间复杂度低，通常采用NTT算法实现多项式乘法。

NTT是定义在有限环上的离散傅里叶变换[16]。假设A(x)为n维多项式，a=(a0，a0，…，an-1)为多项式A(x)的系数向量，则向量a的n点NTT和INTT(Inverse Number Theoretic Transform)定义为

(1)

(2)

式中，n为多项式项数；ωn为有限环上的n次单位根；模数q为素数，且满足q≡ 1mod 2n；n-1为n的逆，满足n·n-1≡1 modq。

将NTT运用于两个n维多项式A(x)和B(x)中，取n维多项式的n维系数向量a=(a0，a0，…，an-1)和b=(b0，b0，…，bn-1)。多项式乘法C(x)=A(x)×B(x)可由C(x)=INTT(NTT(a)⊙NTT(b))得到。值得注意的是，C(x)为2n维多项式，因此在进行NTT运算之前，需要在n维多项式系数向量a和b后填充n个零，使得系数向量维数为2n。填充0后，多项式乘法的时间复杂度将翻倍，为了避免“零填充”，本文采用“负折叠”卷积定理[13]和NTT的算法，如算法1所示，其中ψi和ψ-i为缩放因子。

算法1“负折叠”卷积定理和NTT的多项式乘法。算法步骤为：

步骤1对n维系数向量a、b和ψ=(1，ψ1，ψ2，…，ψn-1)进行点乘运算，得到n维向量aψ和bψ；

步骤2对n维向量aψ和bψ进行NTT运算，得到n维向量A、B；

步骤3对n维向量A、B进行点乘运算，得到n维向量C；

步骤4对n维向量C进行INTT运算，得到n维向量c；

步骤5对n维系数向量c和ψ-1=(1，ψ-1，ψ-2，…，ψ-(n-1))进行点乘运算，得到n维向量cψ，即为多项式乘法运算结果。

1.3 RLWE加密方案

RLWE公钥加密方案定义在多项式环中，而多项式乘法运算是RLWE公钥加密方案最耗时的操作。本文采用“负折叠”卷积定理和NTT加速多项式乘法进行计算。RLWE加密方案算法包括秘钥生成、加密和解密3个步骤[17]，具体流程如算法2、算法3和算法4所示。

算法2公钥和私钥生成算法。具体步骤为：

步骤1在离散高斯分布中选取两个n维向量r1和r2；

步骤2对n维向量a、r1、r2和缩放因子向量ψ=(1，ψ1，ψ2，…，ψn-1)进行点乘运算，得到n维向量aψ、r1ψ、r2ψ；

步骤3对n维向量aψ、r1ψ、r2ψ进行NTT运算，转换到NTT域。NTT运算结果记为A、R1、R2；

步骤4计算P=R1-A⊙R2。其中n维向量(A，P)为RLWE加密方案的公钥，n维向量R2为RLWE加密方案的私钥。

算法3RLWE加密算法。具体步骤为：

步骤1使用编码函数对消息m进行编码，编码结果加上n维向量e3，得到n维向量e3m；

步骤2对n维向量e1、e2、e3m和向量ψ进行点乘运算，得到向量e1ψ、e2ψ、e3mψ；

步骤3对n维向量e1ψ、e2ψ、e3mψ进行NTT运算，转换到NTT域。NTT运算结果记为E1、E2、E3M；

步骤4计算C1=A⊙E1+E2，C2=P⊙E1+E3M，n维向量(C1，C2)为密文。

算法4RLWE解密算法。具体步骤为：

步骤1计算MD=C1⊙R2+C2；

步骤2对n维向量MD进行NTT运算，转换到NTT域。NTT运算结果记为md；

步骤3对n维向量md和向量ψ-1进行点乘运算，得到n维向量mdψ；

步骤4mdψ通过译码函数获得消息m。

2 RLWE加密处理器设计

2.1 整体架构

参数为n=256，q=65 537的RLWE加密处理器硬件架构如图1(a)所示，该硬件电路主要包含3个模块：存储模块、NTT模块、控制模块。NTT模块如图1(b)所示，主要包括倒序模块、预计算模块、蝶形模块、取模模块。存储模块用来存储输入噪声向量、NTT运算过程中的中间系数以及NTT运算后的公钥(A，P)和私钥R2。倒序排列模块用来对输入系数进行倒序排列，然后将倒序后的数据存储到存储模块中。预计算模块用来处理系数，系数乘以ψi，预计算后的数据传递到蝶形模块。蝶形模块用来对输入的系数进行蝶形运算，运算得到的结果经过取模模块处理后存入存储模块。取模模块用来对蝶形运算结果进行取模，保证存储模块输入和输出数据的一致性。控制模块用于控制整个系统，控制存储模块的地址生成及使能，并控制NTT模块进行NTT运算和INTT运算。

2.2 存储模块

存储模块是指图1(a)中的RAM和ROM。存储模块包括6个双端口RAM、两个双端口ROM和1个单端口ROM。图1(a)中，RAM0深度为256，宽度为17 bit，存储e1索引值为0～127的128个数和R2索引值为0～127的128个数；RAM1深度为256，宽度为17 bit，存储e1索引值为128～255的128个数和R2索引值为128～255的128个数；RAM2深度为384，宽度为17 bit，存储e2索引值为0～127的128个数和A；RAM3深度为384，宽度为17 bit，存储e2索引值为128～255的128个数和P；RAM4深度为128，宽度为17 bit，存储e3m索引值为0～127的128个数；RAM5深度为128，宽度为17 bit，存储e3m索引值为128～255的128个数；ROM0深度为256，宽度为16 bit，存储ψ索引值为0～127的128个数和ψ-1索引值为0～127的128个数；ROM1深度为256，宽度为16 bit，存储ψ索引值为128～255的128个数和ψ-1索引值为128～255的128个数；ROM2深度为510，宽度为16 bit，存储NTT运算所需的255个旋转因子和INTT运算所需的255个旋转因子。处理同一批数据时，公钥和私钥不变。因此，本文使用Python脚本语言对公钥(a，p)和私钥r2进行NTT运算，得到公钥(a，p)和私钥R2后存入RAM中。

图1 RLWE加密处理器整体架构图

2.3 预计算和后计算模块

为了减少NTT运算的点数，进而降低多项式乘法器的延迟，本文引入了“负折叠”卷积定理。“负折叠”卷积需要对输入数据进行预计算，并对乘法运算结果进行后计算。预计算和后计算模块电路如图2所示，该模块的输入数据为双端口ROM中存储的缩放因子ψi以及RAM中的系数。对e1和e2同时进行预计算时，e1、e2分别占用两个乘法器，需要n个周期。而对e3m进行预计算时，4个乘法器并行计算，需要n/2个周期。整个预计算过程共需3n/2个周期。在解密过程中，在INTT运算的最后一级，图1(b)中蝶形模块0和蝶形模块1的计算结果乘以缩放因子ψ-i后存入RAM4中。INTT运算结束后，从RAM5中读取两个数据，乘以缩放因子ψ-i后存入RAM5。

图2 预计算和后计算模块

2.4 蝶形模块

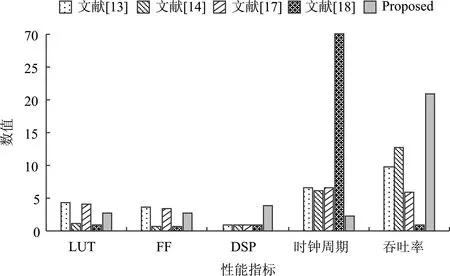
蝶形模块包括通道选择器和基2蝶形单元两部分。通道选择器负责选择输入数据，基2蝶形单元负责计算。蝶形模块两输入之间的间隔(gap)为2stage，stage∈[0，7]，stage表示NTT运算级数。当stage<7时，gap≤64，从同一个RAM中读取蝶形模块两个输入。当stage=7时，gap=128，而RAM深度为128，因此蝶形模块两个输入需要分别从两个RAM中读取一个数据，通道选择器负责选择蝶形模块的输入数据。蝶形运算符号如图3(a)所示，输入数据A、B和旋转因子C，经过蝶形运算后输出A+C×B，A-C×B。当A

图3 蝶形运算

2.5 取模模块

本文选择的模数q=65 537，如果要实现17 bit的数据操作，那么每一个运算结果都需要取模运算，这会占用大量硬件资源。对于模数q=65 537，有232modq=1，为避免每个运算结果都进行取模运算，本文将数据位宽扩展为32 bit。超过32 bit的部分加上低于32 bit的数据，得到33 bit数据。为了降低数据的存储量，将RAM的数据位宽设为17 bit。为了统一输入输出位宽，本文通过对蝶形运算的输出结果进行取模，将数据位宽从33 bit降为17 bit。取模模块电路如图4所示。

图4 取模模块

2.6 乘法器时分复用模块

乘法器时分复用时序如图5所示，图中e1ψ、e2ψ、e3mψ表示对多项式系数向量e1、e2、e3m的预计算过程；E1、E2、E3M表示e1ψ、e2ψ、e3mψ的NTT运算过程；C1表示密文C1计算过程，即A⊙E1+E2；PE1表示P⊙E1过程；C1R2表示C1⊙R2过程；md表示MD的INTT运算过程；mdψ表示md后计算过程。

图5 乘法器时分复用时序图

乘法器控制模块如图6所示，通过选择端sel控制乘法器的时序，不同时间处理不同的数据。从图5可以看出，e1、e2预计算过程分别采用两个乘法器并行处理；e3m预计算过程采用4个乘法器并行处理；e1ψ、e2ψ进行NTT运算过程中分别采用两个乘法器做并行蝶形运算；e3mψ进行NTT运算过程采用两个乘法器做并行蝶形运算，NTT运算过程中，利用另外两个乘法器计算C1和PE1，将这部分乘法运算时间隐藏到NTT运算过程中；C1R2过程采用4个乘法器并行计算；MD进行INTT运算的最后一级，两个乘法器进行蝶形运算，另外两个乘法器对md进行后计算；NTT运算结束后，采用4个乘法器md进行后计算。该方法充分利用乘法器进行并行计算，减少了加密解密的时钟周期，提高了加密处理器的吞吐率，另外预计算、后计算及产生密文过程中复用NTT模块中的乘法器，INTT运算过程复用NTT模块，降低了硬件资源消耗。

图6 乘法器时分复用模块

加密和解密运算过程如下文所示。在进行加密操作过程中：(1)从RAM0、RAM1和RAM2、RAM3读取e1和e2，并分别输入到乘法器Mul0、Mul1和Mul2、Mul3中进行预计算，得到e1ψ和e2ψ，并分别写入RAM0、RAM1和RAM2、RAM3中；(2)e1ψ和e1ψ分别输入蝶形模块0和蝶形模块1进行并行NTT运算，得到E1和E2并分别写入RAM0、RAM1和RAM2、RAM3中；(3)从RAM4和RAM5读取e3m输入到4个乘法器Mul0～Mul3中进行预计算，得到e3mψ；(4)将e3mψ输入到蝶形模块0进行NTT运算，得到E3M并写入RAM4、RAM5中；(5)与此同时分别从RAM2和RAM3中读取A和P，与ROM0、RAM1中的E1进行乘法运算，得到密文C1=A⊙E1+E2和P⊙E1，并分别存入RAM2、RAM3和RAM0、RAM1中；(6)在e3mψ进行NTT运算的最后一级，从RAM0、RAM1读取P⊙E1进行加法运算，得到密文C2=P⊙E1+E3M，并存入RAM4、RAM5中。

在进行解密运算过程中：(1)分别从RAM2、RAM3和RAM4、RAM5中读取C1和C2的4个数，并从RAM0和RAM1中读取R2的4个数，使用两个乘法器并行计算，算得到MD=C1⊙R2+C2并存入RAM2、RAM3中；(2)对MD进行倒序排列；(3)对MD进行INTT运算，在INTT运算的最后一级乘以缩放因子ψ-i。

图7为RLWE加密处理器周期数。从图中可以看出该架构所有的串行和并行操作。该硬件架构充分利用了乘法器并行计算，和串行计算相比，减少了加解密的时钟周期，加快了加密解密速度，提高了加密处理器的吞吐率。其中Vi表示第i个操作得到输出结果所需的时钟周期数量。具体操作如图7左边编号所示。图中步骤0～12符号表示与算法3、算法4一致；rearrange操作在算法3和算法4中未给出，其表示倒序排列。Vi的具体数值如图7所示，加密时钟周期为V0+V2+V4+V5，解密时钟周期为V9+V10+V11+V12。代入图7中的数值可得该架构的加密和解密时钟周期，即加密的时钟周期为nlogn+3n/2+8，解密的时钟周期为n/2logn+11n/4+4。

图7 RLWE加密处理器周期数

3 实验结果与分析

为了验证所提设计方法的正确性，本文在CPU平台和FPGA平台上分别进行了仿真验证。CPU平台为Intel(R)Core(TM)i5-8500处理器，主频为3 GHz。基于Spyder集成开发平台，本文使用Python脚本语言实现了RLWE加密方案。FPGA平台为Spantan-6 xc6slx9-2cpg196，设计语言为Verilog HDL，设计软件为ISE14.7和modelsim10.6d。RLWE加密方案中的离散高斯采样器使用随机函数代替，产生多项式e1、e2、e3后，使用Python脚本语言对公钥(a，p)和私钥r2进行NTT运算。在得到公钥(A，P)和私钥R2后，按照章节3.2所述的存储方式存入存储单元中。实验结果表明，在两个平台上运行的结果一致，验证了本文所提出的硬件实现方法的正确性。使用ISE14.7综合工具进行综合，综合得到的电路数据如表1所示，其中时钟频率为195.4 MHz，LUT数量为2 957，FF数量为2 846，DSP数量为4，加密的吞吐率为21.01 Mbit·s-1，解密吞吐率为29.6 Mbit·s-1。

表1 Spartan-6 FPGA综合结果

表2给出了本文与部分已发表文献的综合结果比较。对比对象全部采用RLWE加密方案，但是采用的实现方式各不相同。表中memory一栏中的指数1表示BRAM18；指数2表示BRAM9；指数3表示BRAM8。文献[18]设计了一个可扩展的处理器，支持两种不同安全等级的RLWE加密方案，该方案需要大量的存储资源(14BRAM)。文献[14]提出了一种资源高效的硬件架构，但是该架构加密、解密的时间较长，吞吐率较低，加密和解密时间分别为4.5 ms和0.9 ms，吞吐率分别为0.056 Mbit·s-1和0.284 Mbit·s-1。相较于文献[14]，文献[19]提出的硬件架构使用更少的硬件资源实现了更快的加速。文献[19]的架构采用Schoolbook乘法实现了RLWE加密方案，该架构硬件面积小，但是Schoolbook乘法器的时间复杂度高，因此加密解密的时间较长。文献[14]采用了串行架构，依次对e1、e2、e3m进行NTT运算，运算时间为单次NTT运算的3倍。但是，文献[14]只用一个DSP乘法器来加解密运算(如算法3和算法4所示)中的点乘运算均串行执行，因此加密解密的时间较长，吞吐率较低。文献[3]所提出的硬件架构中蝶形单元采用了基8算法，由于n=256不是8的方幂，于是该研究实现了n=512的加密器。从实验数据可以看出，该架构吞吐率高，但是硬件面积大，不适合在资源受限的FPGA开发板上实现。针对这个问题，本文采用两个NTT模块和4个蝶形模块的并行结构，在预计算和后计算过程中利用4个蝶形模块中的乘法器进行并行计算；在加密过程中，NTT运算与密文计算并行处理，同时在NTT以及INTT运算的处理过程中，将数据的读写过程及计算过程进行乒乓操作，从而隐藏数据的读写周期，降低RLWE加密处理器的延迟，提高了RLWE加密处理器的吞吐率。加密过程和解密过程的资源消耗和性能对比如图8和图9给所示，其中，LUT、FF、时钟周期单位为k(1k=2)个，吞吐率单位为Mbit·s-1。从图8和图9可以看出，本文提出的RLWE加密处理器时钟周期最少，加密周期数为2 440，解密周期为1 732；在195.4 MHz时钟频率下，吞吐率最高，加密的吞吐率达到了21.01 Mbit·s-1，解密的吞吐率达到了29.60 Mbit·s-1。本文设计了资源复用控制电路，复用乘法器和取模模块进行计算：两个NTT模块复用控制信号，NTT和INTT运算过程重用NTT模块，节省了硬件资源。本文在Spartan-6开发板上进行综合，LUT数量为2 957，FF数量为2 846，硬件面积适中，适合在资源受限的开发板上实现。

表2 RLWE加密处理器性能比较(n=256)

图8 加密过程LUT、FF、DSP、时钟周期和吞吐率对比图

图9 解密过程LUT、FF、DSP、时钟周期和吞吐率对比图

4 结束语

本文提出了优化的高性能RLWE加密处理器硬件架构，设计并实现一种高性能的基于RLWE的全同态加密处理器。该电路采用两个NTT模块和4个蝶形模的并行电路结构，充分利用4个蝶形模块中的4个乘法器进行并行计算，将密文计算过程隐藏在NTT运算过程中，将后计算隐藏在INTT运算过程中，从而减少了RLWE加密处理器的时钟周期，提高了RLWE加密处理器的吞吐率。同时，设计资源复用控制电路、复用乘法器和取模模块进行计算。两个NTT模块复用相同的控制信号，NTT和INTT运算过程重复调用NTT模块，以降低硬件资源消耗。本文设计了参数为n=256，q=65 537的RLWE加密处理器，并在Spartan-6 FPGA上完成了电路实现及电路测试。测试结果显示，完成1次加密只需要12.18 μs，吞吐率达到21.01 Mbit·s-1；完成一次解密只需要8.65 μs，吞吐率达到29.60 Mbit·s-1。该结果表明，该硬件架构可以显著降低延迟，提升RLWE加密器的吞吐率，从而提升加密器的性能，使加密器更具有实用性。该硬件电路适用于大数据、高吞吐率的应用场景。本设计的电路面积仍有可降低的空间，因此未来将重点设计并实现高资源效率的RLWE加密器。