Wolfe 线搜索下具有充分下降性的混合共轭梯度法

2022-11-11房明磊丁德凤

长春大学学报 2022年8期

房明磊，丁德凤，王敏

(安徽理工大学数学与大数据学院，安徽淮南 232001)

考虑无约束最优化问题：

其中f:Rn→R是一个光滑的非线性函数，梯度函数g(x)存在。为方便起见，令gk=∇f(xk)，Gk=∇2f(xk)，yk-1=gk-gk-1，sk-1=xk-xk-1。共轭梯度法是求解上述无约束优化问题的常见有效方法之一，它的迭代公式为：

xk+1=xk+αkdk，

(1)

(2)

其中，αk为步长，dk表示搜索方向，βk为标量。不同的βk公式对应不同的共轭梯度法，经典的βk公式有Fletcher-Reeves[1]，Ploak-Ribiere-Polyak[2][3], Hestenes-Stiefel[4]等，具体形式如下：

(3)

许多文献在这些已有方法的基础上，对βk进行了深入的研究，提出新的混合共轭梯度法。

乌彩英[5]结合牛顿法，提出改进的PRP共轭梯度法：

(4)

该算法结合了牛顿法和PRP算法的优势，在Wolfe线搜索条件下满足充分下降条件和全局收敛性。

Snezana S和Djordjevic[6]针对LS和FR方法，提出混合共轭梯度法：

(5)

其中，参数θk∈[0,1]。证明该混合共轭梯度法产生的搜索方向，不依赖于任何线搜索满足著名的D-L共轭条件，同时在合适的条件下与牛顿方向一致，算法在强Wolfe线搜索条件下具有充分下降性和全局收敛性。

Sarra Delladji[7]采用PRP和HZ方法的凸组合方式提出混合共轭梯度法：

(6)

该算法在最优解附近具有最速下降方向，在Wolfe线搜索下具有充分下降性和全局收敛性。

受上述文献混合方式的启发，基于文献[5]考虑修正PRP共轭梯度法，提出如下的βk更新方式：

其中，0≤θ≤1，并证明了新方法在Wolfe条件下的充分下降性和全局收敛性。

1 新的混合共轭梯度算法

(7)

(8)

使用泰勒展开式，近似得到:

(9)

其中，0≤θ≤1。新提出的方法下降方向为:

(10)

显然，当θ=0时，(10)变为PRP共轭梯度法，当θ=1时，(10)还原为牛顿法。

算法：(NEW)

步骤1：取x1∈Rn，ε≥0，d1=-g1，k=1，如果‖g1‖≤ε，停止迭代;

步骤2：用Wolfe线搜索计算步长αk;

步骤3：令xk+1=xk+αkdk，gk+1=g(xk+1)，如果‖gk+1‖≤ε，停止迭代;

步骤5：令k=k+1，返回步骤2。

2 充分下降条件

(i)假设(H)在水平集L(x1)={x∈Rn:f(x)≤f(x1)}的一个邻域U内，函数f(x)连续可微，梯度函数g(x)满足Lipschitz条件，即存在常数L>0使：

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈U，

(11)

(ii)水平集L(x1)是紧集。

步长αk由Wolfe线搜索准则得到：

(12)

(13)

其中,0≤ρ≤σ≤1，δk=(1-c)‖gk‖2/(Lk‖dk‖2)，αk=max{δk,δkρ,δkρ2,…}。

注：在文献[8]中提出了Lk的一些估算方式，这里设L1>(1-c)L。

(14)

其中,c1=(1-θ)(L1-L(1-c))/L1。

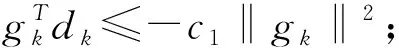
当k>1时，假设结论成立。由Wolfe线搜索

(15)

所以：

(16)

由假设条件(H)，Wolfe线搜索和PRP公式有：

(17)

因此：

(18)

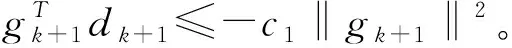
性质*[9]考虑一般的共轭梯度法，假设对所有的k≥1有：

在此假设下，此方法具有性质*：存在常数b>1，λ>0，使得对所有的k均满足|βk|≤b，

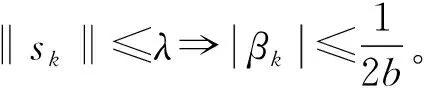
引理2 设目标函数满足假设条件H，如果存在常数γ>0，对所有的k≥1，使得‖gk‖≥γ均成立，则公式(2.4)具有性质*。

证明：由L(x1)的紧密性，存在常数M1>0，使得对所有的x∈L(x1)均有‖xk‖≤M1。根据Wolfe线搜索的条件，得到：

(19)

(20)

(21)

3 算法的全局收敛性

(22)

此关系式称为Zoutendijik条件。

定理1 设目标函数满足假设条件H，考虑公式(2.4)，其中αk满足Wolfe搜索条件，则有：

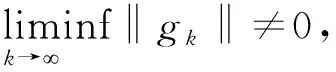
‖gk‖≥ζk=1,2,3…，

根据定理1和引理3，得到：

(23)

因此，

(24)

从引理1可知，{f(xk)}是单调递减数列，并由αk的选取方式有：

(25)

从而得到：

(26)

(27)

(28)

这与式(23)矛盾，故定理成立。

4 数值实验结果

本算法的实验问题选取文献[11]中的部分测试函数集如表1所示，实验结果如表2所示，分别从迭代次数(NI)、梯度函数计算次数(NG)和目标函数计算次数(NFF)与HS方法和PRP方法进行比较，应用文献[12]提供的性能图对实验效果进行刻画。测试环境为处理器11th Gen Intel(R) Core(TM) i5-11300H @ 3.10 GHz，RAM为16 G的计算机，软件平台是Matlab R2021a。实验选取的参数如下：ε=10-6，δ=0.02，σ=0.2。算法的停止准则为以下两者情形之一：(1) ‖gk‖<ε; (2)迭代次数超过1 000次。