五阶KdV方程的行波解、周期波解及其渐近分析

秦春艳

(宿州学院 数学与统计学院，安徽 宿州 234000)

众所周知，在非线性科学中，研究变系数非线性演化方程具有重要的作用，特别是求精确解的问题。因此，研究非线性偏微分方程的精确解是有重要意义的。精确解有很多种类型如孤子解、行波解、周期波解、复解、有理解等。过去的几十年里，在孤子理论中，有很多求解精确解的方法。成功的求解方法是Hirota双线性方法[1]，反散射变换方法[2], 达布变换法[3]、Tanh-coth法[4]、齐次平衡法[5]、李对称方法[6]等等。在这些方法中，Tanh-coth法是一种强大的方法，在处理各种非线性色散方程中已得到广泛的应用，本文正是利用它来求五阶KdV方程的行波解。Hirota双线性方法是其中重要的一种构造非线性偏方程孤子解的简便方法，更重要的是该方法与Riemann theta函数相结合可以得到方程的周期波解。

本研究首先利用Tanh-coth法研究五阶KdV方程的行波解：

ut+αu2ux+γuuxxx+βuxuxx+uxxxxx=0

(1)

考虑到在文献[7]中，上述五阶KdV方程的双线性形式、可积性、孤子解和1-周期波解及其渐近性分析已经被研究，接下来重点讨论如下广义的五阶KdV方程：

ut+h1u2ux+h2(uuxxx+uxuxx)+h3uxxxxx=0

(2)

1 Tanh-coth法

为了得到方程的行波解，下面简单介绍一下此方法，主要分为以下几个步骤：

(i)令波变量ξ=x-ct,则u(x,t)=u(ξ),从而可以将非线性的偏微分方程Ρ(u,ut,ux,uxx,uxxx,…)=0转化成常微分方程Q(u,u′,u″,u‴,…)=0。然后只要常微分方程所有项都包含导数,对它关于ξ积分,积分常数被认为是0。

(ii) 引入一个新的自变量Y=tanh(μξ),ξ=x-ct,其中，μ是波数,于是可以得到：

(iv) 分别将(2)和(3)步骤中的式子代入(1)步骤中所得到的常微分方程,通过合并同类项,并令Y的各次幂的系数为零就可以得到关于c,μ,a0,a1,a2,b1,b2的方程组，求解这些代数方程组，得到它们的数值,进而也就得到所求方程的解u(x,t)。

2 五阶KdV方程的行波解

利用上述Tanh-coth法，首先对方程(1)做如下变形：

利用波变量ξ=x-ct, 然后关于ξ取一次积分，则上述方程可以转化为：

(3)

第一种情况：

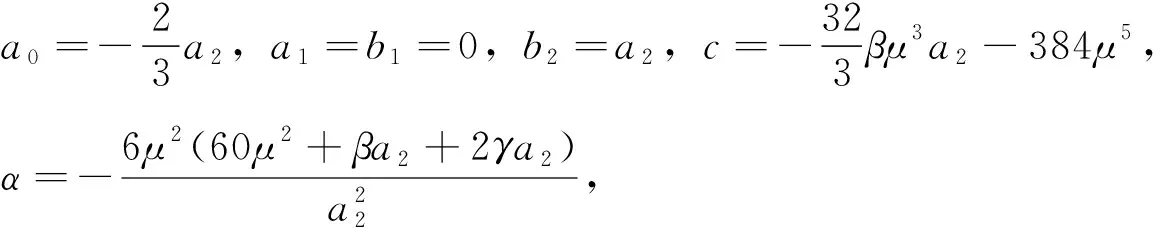
第二种情况：

a0=A, (A是一个常数)，

对于第一种情况，可以得到五阶KdV方程(1)的行波解如下：

同理，对于第二种情况，可以得到五阶KdV方程(1)的行波解如下：

3 广义的五阶KdV方程的2-周期波解

3.1 双线性形式、二孤子解和Riemann theta函数

为了下一小节构造2-周期波解，首先，根据文献[7]中的结果，很容易得出：

定理1：在5h1h3=h22的条件下，通过考虑变换u=30h2-1h3(lnf)xx，广义的五阶KdV方

程有如下的双线性表示：

Ξ(Dx,Dt)≡(DxDt+h3Dx6+δ)f·f=0,

(4)

其中Dx,Dt表示双线性算子，δ=δ(t)是积分常数。

同样地，它的二孤子解具有如下形式：

(5)

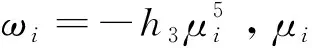
然后简单回顾Riemann theta函数的内容，考虑以下多维Riemann theta函数：

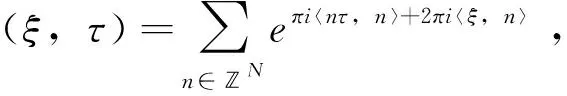
(6)

其中n=(n1,…,nN)T∈N是整数值向量，复相位变量ξ=(ξ1,…,ξN)T∈N。此外，对于两个向量f=(f1,…,fN)T和g=(g1,…,gN)T，它们的内积被定义为：

〈f,g〉=f1g1+f2g2+…+fNgN。

-iτ=(-iτij) 是一个正定实值对称的N×N矩阵，可以称之为Riemann theta函数的周期矩阵。周期矩阵中的元素-iτ可以看作是Riemann theta函数的自由参数。在这种情况下,傅里叶级数(6)收敛于一个带有任意向量ξ∈N的实值函数。

3.2 2-周期波解和它的渐近性

为了构造广义的五阶KdV方程的2-周期波解，考虑双线性方程(4)的更广义的形式。假设方程(2)满足非零渐近条件，即当|ξ|→0时，u→u0，则引入一个变量变换：

u=u0+30h2-1h3∂x2lnϑ(ξ),

(7)

其中，u0是方程(2)的常数解，相位变量ξ的形式为：

ξ=(ξ1,…,ξN)T,ξi=kix+ωit+εi,i=1,2,…,N

将(7)代入方程(2)中并关于x取积分，可以得到新的双线性方程为：

Θ(Dx,Dt)ϑ(ξ)·ϑ(ξ)=(DxDt+h3Dx6+u0h3Dx6+c)ϑ(ξ)·ϑ(ξ)=0

(8)

这里，c=c(t)是积分常数。在文献[8]中，利用多维Riemann theta函数提出了构造非线性偏微分方程的Riemann theta函数周期波解的两个重要定理。现在根据这一结果，可以直接得到广义的五阶KdV方程的2-周期波解。

3.2.1 2-周期波解

定理2：假设Riemann theta函数ϑ(ξ,τ)中N=2,ξi=kix+ωit+εi,(i=1,2)，则广义的五阶KdV方程有如下形式的2-周期波解：

u=u0+30h3h2-1∂x2lnϑ(ξ1,ξ2,τ),

其中，ω1,ω2,u0和δ满足公式H(ω1,ω2,u0,δ)T=b, 这里：

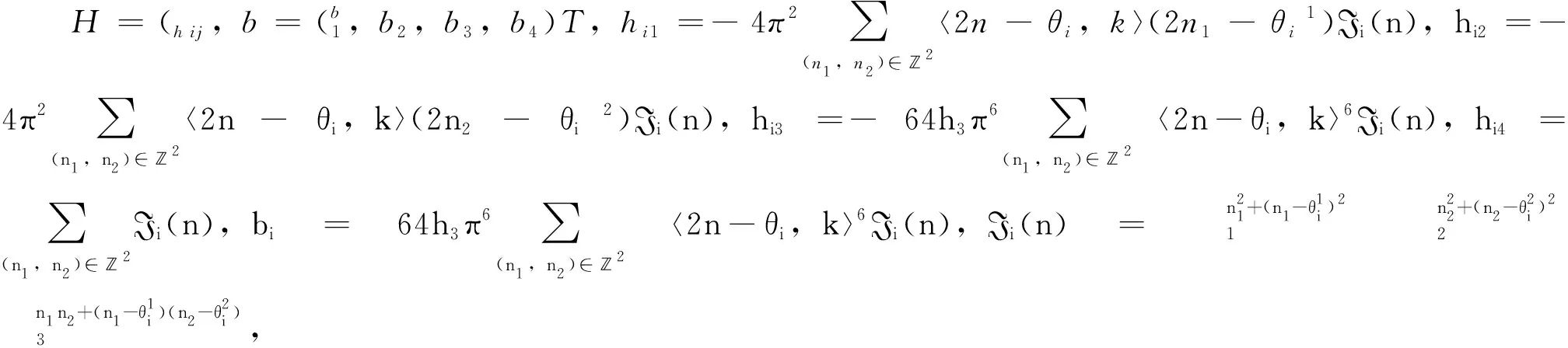
证明：为了得到方程(2)的2-周期波解，考虑下面的Riemann theta函数取N=2，

(9)

其中n=(n1,n2)T∈2,ξ=(ξ1,ξ2)T∈2,ξi=kix+ωit+εi,(i=1,2) 和-iτ是实值正定对称2×2矩阵，它可以写成下面的形式：

注意到方程(8)的特殊形式，如果下式成立，则可以得到2-周期波解：

结合方程(8)和上面的表达式，得到：

上述方程可以转化为如下形式：

(10)

对上面的式子进行求解，可以得到方程(2)的2-周期波解：

u=u0+30h3h2-1∂x2lnϑ(ξ1,ξ2,τ)

(11)

其中，ϑ(ξ1,ξ2,τ)和参数ω1,ω2,u0,δ分别由(9)式和上述方程来确定，其他参数ki,τij和εi(i,j=1,2)是任意的。

通过选取合适的参数，绘制了广义的五阶KdV方程的2-周期波解的传播情况，如图1和图2所示。

图1 k1=-2,k2=3,τ11=i,τ12=0.5i,τ22=2i,ε1=1.5,ε2=0,h2=1,h3=2时周期波解的传播情况

图2 k1=1,k2=1.5,τ11=i,τ12=0.15i,τ22=2i,ε1=ε2=0,h2=2,h3=4时周期波解的传播情况

2-周期波解有下面的简单特征:

(i)它的表面是二维的, 也就是有两个相变量ξ1和ξ2, 它表明2-周期波在两个独立的水平方向有两个独立的空间周期。

(ii)在(ξ1,ξ2)中, 它有2N个基本的周期{ζi,i=1,2,…,N}和{τi,i=1,2,…,N}。其中

ζ1=(1,0,…,0)T,…ζN=(0,0,…,1)T。它的传播速度是:

(iii)假如ki,li满足下面的关系:

可以得到：

ω2～mω1,ξ2～mξ1,ϑ(ξ1,ξ2)～ϑ(ξ1,mξ1) 。

2-周期波其实是一维的并且它可以退化为1-周期波。

3.2.2 渐近性质

在本小节中研究广义的五阶KdV方程的2-周期波解的渐近性。

定理3：如果(ω1,ω2,u0,δ)T是方程(10)的一个解，对于2-周期波解(11)，取：

(12)

其中μi,δi,i=1,2和A12可以由方程(5)得到，则有下面的渐近关系：

证明：周期波函数ϑ(ξ1,ξ2,τ)可以展开为如下形式：

ϑ(ξ1,ξ2,τ)=1+(e2πiξ1+e-2πiξ1)eπτ11+(e2πiξ2+e-2πiξ2)eπτ22+(e2πi(ξ1+ξ2)+e-2πi(ξ1+ξ2))eπ(τ11+2τ12+τ22)+…

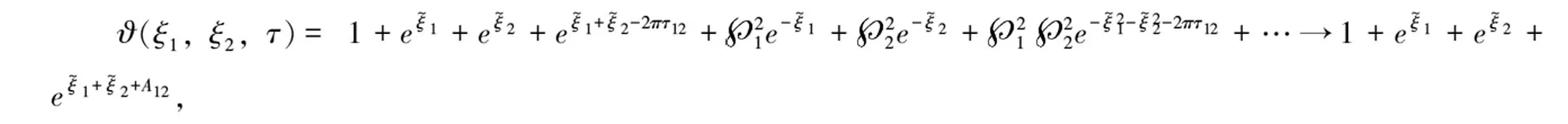
(13)

其中，Δ,Υ分别为：

4 结语

本研究利用Tanh-coth法，得到了五阶KdV方程的行波解，然后借助Riemann theta函数周期波解的方法，构造了广义的五阶KdV方程的周期波解。并对周期波解和孤子解之间的关系做了分析，证明了参数在一定的极限条件下，周期波解趋近于孤子解。那么，所采用的求解方法对其他非线性偏微分方程是否适用以及还有没有其他方法可以用来对五阶KdV方程进行研究，这都是值得思考的问题，需要以后进一步的研究。