基于定性定量混合建模的金湿法冶金过程优化研究

高 军，刘亚东

(1.东软集团股份有限公司，辽宁 沈阳 110819；2.东北大学信息科学与工程学院，辽宁 沈阳 110819)

0 引言

随着湿法冶金行业的规模化、集中化和连续化生产，全厂范围的湿法冶金工艺优化比局部优化可以获得更高的经济效益，更有利于提高生产效率和产品质量[1-2]。因此，对湿法冶金过程的全厂优化进行研究具有重要意义。

目前，湿法冶金工艺优化的研究主要集中在典型工艺的优化上，如浸出[3]、浓密洗涤[4]、置换[5]等。在整个湿法冶金生产过程中，每个典型过程都有自己的优化指标，它们之间相互关联、相互制约。因此，仅依靠每个子过程的优化不能解决湿法冶金过程的全厂优化问题，需要从全流程过程的高度做出总体决策并协调各个子过程[6]。近年来，对湿法冶金工艺的全厂优化研究甚少。为了快速有效地解决大规模工业过程的全流程优化问题，基于单元过程之间的耦合关系，YUAN等[7]提出了一种新的全流程优化方法。考虑到湿法冶金过程中的选矿过程，为了实现综合生产指标的优化，基于物料平衡关系，YU等[8]建立了全流程选矿优化模型，并用改进的遗传算法求解优化模型。

随着生产规模的扩大和复杂性的增加，工业过程的调节和运行涉及大量不确定因素，严重影响了工业生产的稳定性和可靠性。高亚东等[9]针对湿法冶金生产过程调浆子过程中矿浆浓度的不确定性，提出一种区间全流程分层优化方法。王湘月等[10]针对湿法炼锌除铜过程入口铜离子浓度和溶液流量的不确定性，提出一种机会约束优化控制方法。ZHANG等[11]针对湿法炼锌除铜过程出口铜离子浓度的不确定性，基于氧化还原电位与铜离子浓度之间的关系，提出一种模糊不确定优化方法。然而，在随机规划中，将不确定参数视为随机变量，并假定其概率密度函数已知。在模糊规划中，将不确定参数看作模糊数，假定其模糊隶属度函数已知，将参数约束范围看作模糊集。由于在实际工业生产过程中，不确定变量的分布通常很难满足上述两种假定条件，通常是无规律的且模糊隶属度很难准确得到。而区间规划研究的是不确定参数以区间形式进行描述的优化问题，无需知道其准确分布和隶属度函数。

姜潮[12]详细描述了区间优化方法的理论，利用区间描述变量的不确定性，只需要通过较少的信息获得变量的上下界。为了解决优化模型中存在不确定区间型变量的过程优化求解问题，区间优化方法采用区间序关系转化模型将原优化模型的不确定目标函数转化为确定性多目标优化函数；并且采用区间可能度转化模型将原优化模型的不确定约束条件转化为以满足一定概率可能度水平形式描述的确定性约束条件。最终，通过转化模型，得到确定性的两层嵌套优化问题，采用常规的智能优化求解算法，例如粒子群优化算法、遗传算法、序列二次规划等，求解转化后的确定优化问题。基于上述描述，本文采用区间优化方法，根据对不确定区间的处理策略，将湿法冶金初始不确定过程优化模型转化为等价的确定性优化模型。

湿法冶金过程的生产条件和生产环境十分复杂，致使一些工艺参数如流量、成分、金属品位等难以实时在线准确测量。此外，环境的动态变化，如生产原料成分不稳定和生产边界条件剧烈波动等，以及一些重要生产指标(浸出率、洗涤率、置换率等)不可直接测量过程信息的未知性和不完整性等因素，也带来了工业过程的不确定性[13]。若不考虑不确定性，湿法冶金过程的优化结果将难以保障生产流程和产品质量的稳定，造成能源的浪费，甚至影响冶金过程的安全运行。然而，在黄金湿法冶炼过程的优化设计中，关于解决这些不确定性的方法的相关研究并不多，其中大多数研究的是确定性的[14-15]，为了简单起见，忽略不确定性参数对优化结果的影响，导致优化结果不是真实操作条件下的最优操作，甚至是非最优的。

本文针对湿法冶金生产过程压滤脱水调浆子过程中矿浆浓度变量不能准确在线测量，导致该环节无法定量建模，进而不能采用传统优化方法求解的问题，首先利用现场操作人员的经验知识等信息建立该环节的模糊定性模型。其次，将定性模型输出变量值视为不同模态下的边界区间，通过与前后两次浸出过程的定量模型相结合，提出一种基于区间数的优化方法，将不确定优化模型转化为确定性优化模型。再次，采用粒子群优化算法求解转换后的确定性多目标优化问题。最后，通过仿真实例验证了本文方法的有效性。

1 湿法冶金生产过程

湿法冶金工艺流程复杂，通常由磨矿、浮选、压滤脱水、调浆、浸出、洗涤、置换等众多工序构成，且设备类型多样，整个流程具有多变量、变量之间强耦合等综合复杂性，其生产指标容易受原料成分、工况、设备状态等多种不确定性因素干扰[16]。本文研究的湿法冶金工艺基本操作流程如图1所示。首先，精金矿通过脱水调浆后产生矿浆，由排矿泵送入到一次氰化浸出流程的浸出槽中，金氰化浸出过程如图2所示。通过添加氰化钠与矿浆发生浸出反应，实现精矿中金和杂质的分离。其次，将一次浸出后的矿浆通入一次压滤洗涤过程中的压滤机中进行固液分离，分离后的滤饼再次进入调浆环节制成矿浆，压滤脱水调浆过程如图3所示。最后，矿浆再次由排矿泵送入二次氰化浸出过程，通过与氰化钠反应，最终实现对矿石中金的分离。

图1 湿法冶金工艺基本操作流程图

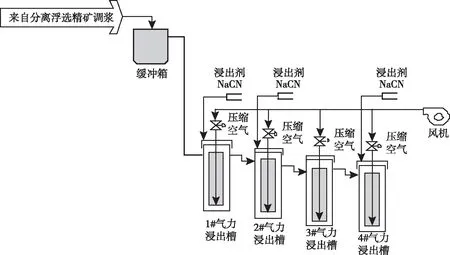
图2 氰化浸出过程

图3 压滤脱水调浆过程图

压滤脱水调浆过程是湿法冶金过程的重要工艺之一，其生产过程和制成矿浆的稳定对于湿法冶金工艺至关重要。由于生产条件的限制，现场中对矿浆浓度的检测不能直接由仪器准确在线测量，同时，其生产过程中存在非线性、大滞后、干扰因素多等问题，使得压滤脱水调浆过程这一局部环节无法建立准确机理模型，进而无法实现基于定量模型的优化求解。在压滤脱水调浆过程中，由于压滤时间的不稳定性，且调浆水的添加通常是根据现场操作人员经验给出，致使调浆后的矿浆浓度发生波动。而矿浆浓度对后续氰化浸出过程影响很大，会直接影响金的溶解速度，浸出率又是浸出过程最重要的工艺指标，其运行性能的优劣直接决定了最终回收金的收益。

因此，为了获得湿法冶金过程最大经济效益，需要对湿法冶金过程进行建模并优化求解。本文通过建立压滤脱水调浆子过程定性模型，用区间数的形式表示矿浆浓度变量不确定性，采用区间优化方法使得过程优化求解得以实现。

2 湿法冶金过程优化模型建立与求解

矿浆浓度的不确定性使得调浆过程与压滤洗涤过程无法建立定量模型，这给基于模型的优化方法实现湿法冶金过程优化求解带来了很大困难。针对这个问题，本文提出了如图4所示的由专家知识模糊定性模型和基于区间数的优化求解模型组成的基于混合模型的湿法冶金过程优化框架。首先，针对压滤脱水调浆过程无法建立定量模型问题，提出一种结合专家知识的定性建模方法。然后，针对该定性模型的每一种输出状态，结合前后二阶段氰化浸出子流程，采用基于区间数的优化方法求得不同输出模态状态下的最优指标和操作条件。最后，建立该混合模型的优化操作模式库。

图4 基于混合模型的湿法冶金过程优化框架

2.1 定性知识模型建立

由于无法通过定量模型来描述压滤脱水调浆过程的动态特性，而矿浆浓度的波动会对后续流程优化操作产生影响，因此，这给湿法冶金过程优化带来了很大障碍。针对该问题，建立一种结合专家知识的模糊定性模型。

对于压滤洗涤过程，结合现场工人经验和相关资料得到历史压滤时间的变化范围为10～15 min[17]，因此将压滤时间t合理划分为3个状态，分别为短(S，10～12 min)、中(M，12～13 min)、长(L，13～15 min)，压滤时间的状态根据专家经验判断获得。对于调浆过程，结合专家知识和现场工人经验得到历史调浆水量的变化范围为30～70 t/h，因此将调浆水量q合理划分为5个状态，分别为最小(NB，30～35)、较小(NS，35～45)、中(ZE，45～55)、较大(PS，55～65)、最大(PB，65～70)，根据调浆水量测量值的模糊化处理获得调浆水的状态。

由于调浆过程出口条件矿浆浓度Cw不可在线测量，通常只能根据现场操作人员经验或专家知识估计其所处范围区间[0.30,0.42]。为此，针对矿浆浓度的不确定性，本文结合专家知识和现场操作人员经验将调浆过程的输出变量(矿浆浓度Cw)划分为5个状态，分别为最小(NB，Cwmin～0.33)、较小(NS，0.30～0.36)、中(ZE，0.33～0.39)、较大(PS，0.36～0.42)、最大(PB，0.42～Cwmax)，矿浆浓度的状态根据矿浆浓度化验值的模糊化处理获得。这样，矿浆浓度Cw的隶属度函数如图5所示。

图5 矿浆浓度的隶属度函数

根据压滤脱水调浆过程的工艺特点，利用过程数据及专家知识得到的模糊规则进行仿真研究，得到了在当前一次浸出过程运行工况下不同调浆水量和压滤时间的变化对矿浆浓度的影响规律。建立压滤脱水调浆过程中调浆水量、压滤时间与矿浆浓度之间的定性关系，如表1所示。

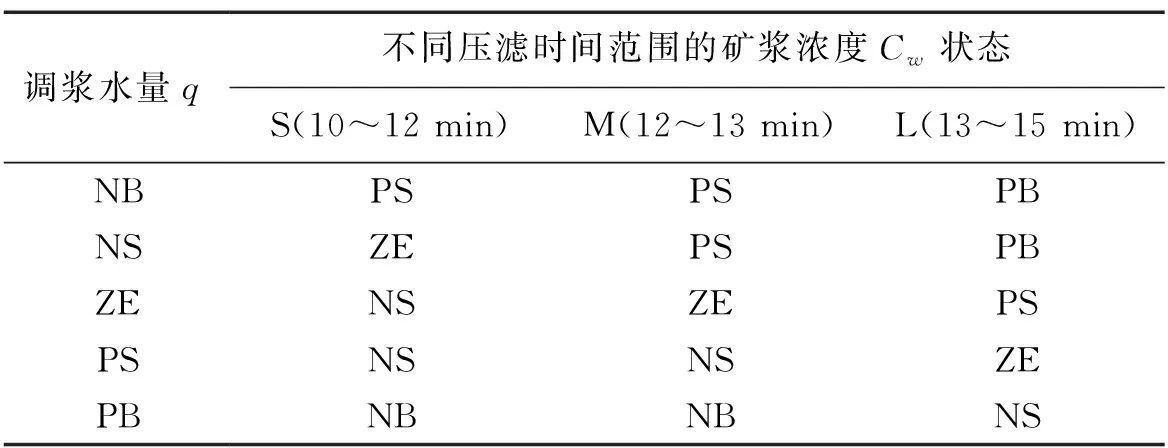
表1 压滤脱水调浆过程模糊规则

在当前一次浸出过程运行条件下，当调浆水量不变时，压滤时间越长，矿浆中的固液分离越充分，调浆后的矿浆浓度越大；当压滤时间一定时，调浆水量越大，调浆后的矿浆越稀。

2.2 优化模型求解

实际生产中，在一定的输入条件下，不同操作参数的生产效益差异很大。为此，考虑矿浆浓度对浸出工序生产指标的影响，对压滤脱水调浆过程定性知识模型的每一个输出模态(矿浆浓度)，对前后二阶段氰化浸出子流程建立定量模型，并优化求解。根据在不同模态下求得的生产成本指标，得到相应的最优操作策略(浸出率、氰化钠添加量、调浆水量和压滤时间)，从而建立混合模型的最优模态库。

浸出过程中对浸出率影响较大的操作变量是氰化钠添加量，对于调浆过程，调浆水量将直接决定调浆后的矿浆浓度。由于压滤洗涤过程的压滤时间长短直接影响进入后续置换过程中贵液里的金含量。所以，过程模型的决策变量选取为6个浸出槽的氰化钠添加量、调浆过程的调浆水量和压滤过程的压滤时间。根据流程工艺生产要求，浸出率和生产物耗需满足：

(1)

通过前文对湿法冶金流程工艺的描述可以看出，矿浆浓度的波动使得浸出过程生产指标浸出率发生改变，同时由于其变量的不确定性特征，使得与之相关的过程变量均表现为不确定性，例如浸出过程末尾浸出槽中的氰根离子浓度和固金品位。本文将矿浆浓度这一定性量转变为不同模态下区间型定量量，定义大致区间边界。以单位时间的最低生产成本作为优化目标，具有不确定性的湿法冶金浸出过程优化模型定义如下：

(2)

为了能够有效求解优化模型(2)，本文假定将操作变量压滤时间和调浆水量在不同模糊集的定性量转化为单值型定量量。

区间数优化中利用基于区间数序关系的转化模型来定性地比较不同目标区间数的大小(好坏)。同时，将区间可能度转化模型用于定量描述一区间大于(或优于)另一区间的程度。因此，本文选择文献[12]提出的一种区间序关系转化模型和区间可能度转化模型来解决式(2)中不确定目标函数之间和不等式约束的关系。

生产成本指标Jm,I可以表示为区间数：

(3)

目标函数范围的中点值和半径值用于判断不同决策向量之间的最优性，如果决策向量x2优于x1，则目标函数区间值Jm,I(x2)优于目标函数区间Jm,I(x1)，即Jm,c(x1)≥Jm,c(x2)且Jm,w(x1)≥Jm,w(x2)。因此，希望找到一个最优的决策向量，使不确定目标函数的范围具有最小的中点值和半径。将(2)中的不确定目标函数转化为确定性多目标优化问题：

(4)

公式(2)中的不确定不等式约束可以转化为如下确定性不等式约束：

(5)

其中

(6)

(7)

基于混合模型的过程优化求解方法的实现流程具体步骤如下：

步骤一 结合专家知识对无法建立定量模型的子流程建立定性知识模型，并将输出变量划分多模态。

步骤二 针对定性模型输出变量每一模态，利用区间数的优化方法对过程模型优化求解，通过求解式(2)～(6)，获得生产成本指标Jm和最优操作参数Qcn,ij(i=1,2;j=1,2,3)、QTJ和T。

步骤三 建立最优操作模态库。

3 仿真及分析

仿真硬件设备：

①CPU处理器：Intel®CoreTMi7 2.9 GHz。

②RAM内存：8 G ddr4 3200。

③硬盘：1 TB。

④软件平台：MATLAB 2019b。

基于实际生产过程数据，给定某种工况条件，在相同的工况条件下，通过与传统确定性优化方法相比，验证本文提出方法的有效性。

3.1 混合建模过程区间优化结果分析

对无法建立定量模型的压滤脱水调浆过程，通过建立定性知识模型得到输出变量矿浆浓度5个定性值[NB、NS、ZE、PS、PB]。通过基于区间数的不确定优化方法求解各个模态中的生产成本指标和最优操作变量，进而建立混合过程的最优模式库。采用PSO算法求解过程优化模型问题，算法的参数设置如下：

①外层操作变量优化：种群规模为100，最大迭代次数为35，惯性权重为0.8，学习因子c1=1.2，c2=0.9。

②内层不确定变量区间优化：种群规模为10，最大迭代次数为50，惯性权重为0.9，学习因子c1=0.95，c2=0.95。约束可能度水平λ1=0.99，λ2=0.85。优化结果如图6所示，并建立最优模式库，如表2所示。

图6 基于混合建模的过程优化结果

图7 不同优化方法优化结果比较

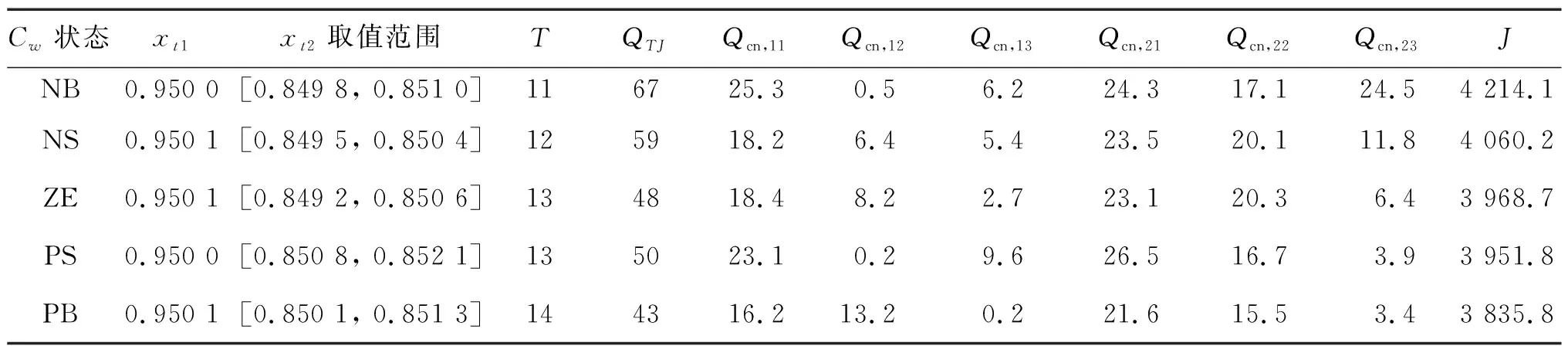
表2 优化结果最优模式库

从图6可以看出，不同矿浆浓度模态取值下，混合模型的生产成本指标不同，随着矿浆浓度值的增大，生产成本越低，也就意味着综合经济效益越大。因此，采用传统的确定性优化方法对存在不确定性过程机理模型进行优化求解得不到准确的操作变量，进而也就不能实现过程的最优控制。从表2也可以看出，由于本文将矿浆浓度变量划分为多模态定性值，并采用区间优化方法对存在不确定性的混合模型进行确定性等价转化。因此，二浸浸出率的结果以区间形式表示。并且，由于一浸浸出过程不受压滤脱水调浆过程中矿浆浓度的影响，只要初始工况条件不变，一浸浸出率不会发生明显改变。这样，从二浸浸出率区间值表述和各个模态下操作变量的不同可以看出，不同矿浆浓度模态下生产成本指标发生明显改变。

3.2 不同优化方法仿真对比分析

为了验证本文方法的有效性，假设压滤脱水调浆过程输出变量矿浆浓度Cw离线化验值为0.36 g/g。对于传统的全流程优化方法，为了计算方便，通常选择不确定变量的近似值或者中间值。在本文的对比仿真实验中，依据传统优化方法中的参数设定，将矿浆浓度Cw假定为定值，即Cw=0.32 g/g。此外，对于随机规划这种不确定优化方法而言，不确定变量假定其概率分布已知，因此，在对比仿真实验中假定矿浆浓度不确定变量服从均值为0.36、方差为0.02的高斯分布。基于上述实验数据分别进行如下仿真实验：基于近似值的过程优化、基于随机值的过程优化、基于概率分布的过程优化、基于真实离线化验值的过程优化和基于区间数的过程优化。上述所有仿真实验的优化求解均采用具有相同优化参数的粒子群优化算法，仿真结果如图7所示，比较结果如表3所示。

表3 不同优化方法的优化结果比较

从图7可以看出，采用传统的确定性优化方法，由于假定不确定变量为一确定数值，优化结果不是真实最优值。而采用本文提出的不确定区间优化方法对混合模型进行优化求解后，优化结果是一个区间型数值，且包含了真实最优值。图7中落在两条虚线区间内的点服从矿浆浓度在该模态下的分布。由于随机规划需要考虑不确定性变量的概率分布特性，存在一定的概率不满足约束，即约束的保守性更强，因此，采用随机规划优化出来的结果也不是最优值。此外，约束不被满足的概率指标是由个人经验根据实际工业生产背景给出的，因此，由于约束满足条件的不唯一性，随机规划优化出来的结果也是随机变化的。综上所述，与传统的优化方法相比，本文方法在过程优化中具有可行性和合理性，可以有效地解决参数不确定的模型建模与优化问题。此外，从仿真实验结果可以得出，基于区间数的过程优化方法比传统的优化方法更为保守，并且能够满足实际生产过程的要求，由此进一步表明本文提出的优化方法具有更好的优化性能。

4 结语

本文分析了湿法冶金生产过程的特点及其建模优化中存在的难点，研究了基于区间数的过程优化方法，提出了湿法冶金过程建模优化的框架。对于存在无法定量建模环节的子流程，基于现场经验建立该环节的模糊定性模型。通过将定性模型与定量模型相结合，针对工业流程中某些子过程存在无法确定的区间变量，采用区间优化方法实现了不确定优化模型的确定性转化。最终将本文方法应用于湿法冶金生产过程中，仿真结果验证了所提建模与优化方法的有效性。