药品物流多中心选址优化研究

袁志远, 高 杰, 杨才君

(1.西安交通大学 管理学院,陕西 西安 710049; 2.西安交通大学 药学院,陕西 西安 710061)

0 引言

为了减轻人民群众用药费用负担，压缩药品利润空间，2018年我国实施了4+7城市药品集中带量采购，截至2020年底，已实施三次，全国性、多种类、大批量、高时效的药品配送成为药品物流面临的新问题。

物流中心是物流系统和供应链良好运行的关键因素[1]。近年来，国内外部分学者对药品物流多中心选址问题进行了研究。如黄玉兰等[2]设计了基于医药企业在离散时间段下的成本最小化数学模型；李小娟[3]借鉴省内外农村药品配送系统优化的成功经验,提出了农村药品配送系统优化措施；尹志鹏[4]对乡镇基本药物的分布进行了研究，发现乡镇基本药品客观上存在供应不及时、品种不全等方面的问题；杨浩等[5]构建了考虑碳排放、带软时间窗的多目标药品冷链物流配送路径优化模型；张晓璐[6]为保障药品运输过程中的质量,通过建立AHP/SWOT相结合的模型,保障物流运输高效运转；Bayan Hamdan等[7]针对灾后血液配送问题，构建了一个双目标稳健优化模型。王凯成等[8]运用AHP法和TOPSIS法最终确定Y药品集团的物流配送中心选址；胡剑玫[9]根据普通药品的配送特点和冷藏药品的配送特点，分别建立了带时间窗的医药物流配送模型。

上述这些研究，一是药品配送或回收中心选址的研究；二是药品弹性供应链的研究。这些研究涉及药品种类较少、数量较小。选址和配送过程中少有涉及制冷成本、环保成本和实时路况。目前还没有针对全国性、多种类、大批量、高时效的药品集中配送研究。

1 问题描述与模型建立

1.1 问题描述

根据各城市集中采购结果，在综合考虑运输往返、往返环保、制冷、货损、库存租赁、药品未按时配送等成本因素及货损对配送量的影响和实时路况，构建药品物流多中心选址-路径优化双目标模型。

1.2 药品配送假设

我们假定：1)各药品企业到各备选药品物流中心，各备选药品物流中心到各城市距离已知，且有多种运输工具供选择；2)备选药品物流中心已知，每个城市每种药品合约采购量已知；3)同一家药品企业可以生产多种药品，可以参与多种药品集中采购招标。

表1 模型参数

1.3 药品配送模型

决策变量：

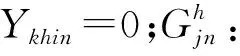
根据以上假设和定义，药品物流多中心选址-路径优化双目标模型表示为:

(1)

(2)

(8)

约束条件(3)每种药的合约采购量与药损量之和小于等于每种药配送总量；约束条件(4)每个城市每种药中标量与药损量之和小于等于每种药配送总量；约束条件(5)表示企业的配送总量大于每个城市药品配送量；约束条件(6)每家企业每种药品配送可以选择多个药品物流中心；约束条件(7)每个城市只能选择一个中心进行配送；约束条件(8)决策变量约束。

2 FCM-TS-SA混合算法设计

2.1 求解思路

利用FCM算法可以求出合理的初始解，不但能缩小搜索范围，而且也可以提高算法计算效率。把禁忌搜索算法运用在模拟退火算法中可以进一步提高算法局部搜索能力，提高运算速度。根据以上算法理论，充分利用各算法的优点，结合实例应用设计出了FCM-TS-SA混合算法。

2.2 算法设计

求解此类问题的方法很多，包括蚁群算法、粒子群算法、禁忌搜索算法、遗传算法等，本文采用FCM-TS-SA混合算法进行求解[10～13]，该算法充分利用了模拟退火算法(SA)、模糊C-均值聚类算法和禁忌搜索(TS)优点，增强了初始解的合理性，提高了算法局部搜索的速度，增强了算法跳出局部最优的能力，提高了寻优效能[14,15]。

(1)设置参数

数据集用X={x1,x2,…,xn}，初始温度用T表示，r表示冷却速率，每个T值迭代次数用L表示，z1表示函数解，s表示禁忌表。

(2)FCM产生初始解

FCM算法是一种以隶属度来确定每个需求点属于某个聚类的算法，模糊C划分采用模糊矩阵U=⎣uij」表示，矩阵U的元素表示第j个药品需求城市属于第i类的隶属度，uij满足以下条件[16,17]:

(9)

本文采用类内加权误差平均和的最小值为聚类准则，即:

(10)

V为聚类中心，m为加权指数，

dij(xj,vi)=‖vi-xi‖

(11)

模糊C均值聚类算法迭代步骤如下：

①用[0,1]之间的随机数初始化隶属矩阵U，使其满足约束条件(9)；

②计算第c个聚类中心记为(i=1,2,…,c)；

③如果函数值小于某个确定阈值，或函数值的改变量小于某个阈值，停止计算，输出结果F(z0)，否则，进行下一步；

④计算新的U矩阵，返回②。

(3)禁忌搜索

禁忌搜索获得新解zi，计算目标函数值F(zi)；

(4)判断新解

计算增量Δt=F(zi)-F(z0)，如果增量小于0，则接受zi为新的当前解z，否则，以exp(-Δt/T)接受zi为新的当前解z；

(5)记录禁忌表

在运算中，如果新得的解与禁忌表中的解相同，则直接跳过。根据每次迭代的结果替换禁忌表中的函数最优解和最优值；

(6)判断迭代终止条件

计算k=k+1，如果k≤L，转第3步，否则，进行下一步；

(7)判断程序终止条件

计算T=r×T，如果T≥0，转第3步，否则，运行下一步；

(8)运算结果

输出最优解。

3 算例分析

3.1 实例应用

某物流公司承接了“阿托伐他汀口服常释剂型”“氯吡格雷口服常释剂型”“头孢呋辛脂口服常释剂型”三种药品配送业务，分别用1、2、3代码表示，中标企业及药品规格如表2，药品生产企业到各需求城市及各需求城市之间的距离如表3，每种车辆运输成本如表4,各参数值如表5。综合考虑运输往返、制冷、往返环保、货损库存租赁、药品时间满意度等成本因素及货损对配送量的影响和实时路况，求药品物流多中心选址-路径优化方案。

表2 4+7带量集中采购部分中标企业及药品

表3 药品生产企业到各需求城市及各需求城市之间的距离(100km)

表4 车辆单位距离运输成本(元/千克)

表5 参数取值及含义

表6 药品物流多中心选址优化方案及成本

3.2 算法对比分析

为了说明本文所设计的FCM-TS-SA混合算法的优越性，针对该问题分别采用遗传算法(GA)、禁忌搜索算法(TS)、蚁群算法(AG)、粒子群算法(PSO)和模拟退火算法(SA)进行了计算，各算法参数设置如表7，运算结果如表8(计算时间取整)。

表7 各算法参数设置

表8 算法运算结果对比分析

通过反复实验我们发现遗传算法(GA)、禁忌搜索算法(TS)、蚁群算法(AG)、粒子群算法(PSO)和模拟退火算法(SA)都能寻找到该问题的最优解，但各算法所用时间不同，FCM-TS-SA混合算法与以上算法相比所用平均时间较短。

4 结论

本文以国家药品集中带量采购为背景，针对全国性、多种类、大批量、高时效的药品配送新问题。构建了药品集中配送多中心选址-路径优化双目标模型。设计出了FCM-TS-SA混合算法，并通过与多种算法进行对比，验证了该算法的可行性和优越性。本文没有考虑突发自然灾害下药品集中配送问题，因而，综合考虑突发自然灾害，药品集中配送问题将是作者下一步研究的内容。