基于遗传算法的生产线多目标优化研究
2022-11-10贺田龙邵明国白晓庆李艳鹏
贺田龙 邵明国 白晓庆 曹 泽 李艳鹏
(①中车永济电机有限公司,山西 永济 044502;②轨道交通牵引电机山西省重点实验室,山西 永济 044502)
在生产线规划设计阶段,仿真及优化是生产线规划设计的重要技术。仿真能够评估、验证生产线设计方案的合理性、可行性[1];仿真优化能够对生产线设计方案进行量化分析,求出最优解,使生产线性能整体最佳。
在实际生产中,生产线规划方案的优劣,决定着产线布局及投产后的运行状态,而物料流动是产线生产运行时的一个显著特征。在产品量产时,物料配送影响产线的准时制生产。当物料提前配送到工位时,会在工位附近形成物料累积,占用工位作业空间;当物料滞后配送到工位时,工位因缺少物料而暂时停止生产,降低产线生产效率。
因此,生产线规划设计需要考虑多种因素对产线方案实施后造成的影响,而设计人员依靠知识和经验,对产线动态生产过程一般不能给出最佳规划方案[2],往往需要在方案实施后根据产线运行状况进行调度调试。这种传统的设计方法,不能满足产线快速设计的要求,导致产线延期投产。然而,随着计算机和工业仿真软件的发展,运用仿真及优化技术能够对生产线方案进行验证及优化,缩短设计周期,提高设计质量,如:将仿真优化技术应用到生产线产能优化方案中,通过仿真试验使产能最大化[3];将遗传算法和有限扰动分析相结合进行生产线仿真优化,提高产线生产效率[4];开发通用离散事件仿真模型进行布局规划,使总生产时间最小化[5]。
1 问题描述
某产品生产线初步规划方案如图1 所示。该产线规划方案基于精益思想,采用“U”型布局[6],产线内侧布置有AGV 轨道,用于AGV 自动配送物料。

图1 生产线初步规划设计图
生产线规划方案要求,在产线正常运行情况下,产品生产周期(首个产品下线至末端产品下线所需时间)满足最大日产量要求,即生产线双班制15 h内完成480 个产品日产量需求。AGV 装载与卸载时间各为20 s,同时要求暂存区总容量尽可能最小化、设备平均利用率及AGV 平均利用率尽可能最大化。
2 生产线方案分析
产品生产工艺流程包括10 个工位分别为工位1、工位2、工位3、工位4、工位5、工位6、工位7、工位8、工位9、工位10,各工位按照工艺流程依次布置。工位信息如表1 所示,其中,工位3 和工位8 各布置4 个并行工序、工位9 布置8 个并行工序,各工位标准作业时间存在较大差距,工位9 作业时间最长,节拍为900 s,属于瓶颈工序。当该工位处于作业状态时,会导致在制品堵塞;当该工位接收在制品时,会减少在制品累积数量。因此,工位暂存区容量影响产线布局及运行状态。

表1 工位信息
在生产线运行过程中,处于等待状态的空载AGV 接收到指令后,自动将需要的物料在需要的时候配送到指定工位,实现工位物料精准配送[7],从而保证产线高效生产。AGV 作为生产线中物料配送的载体,是保证物料顺畅流动的关键组成部分,AGV 的数量、配送量及速度等参数是产线设计的重要参数。然而,生产线初步方案中AGV 的数量、配送量及速度参数并不确定,这些参数对产线生产周期、暂存区总容量、设备平均利用率及AGV 平均利用率目标的影响,是设计产线方案时需要考虑的内容。通常情况下,各目标之间会制约,多个目标并不能同时达到最优[8]。因此,需要对产线方案进行建模仿真,通过仿真试验研究生产系统,以探究各因素之间的作用规律,从而更好地规划产线方案。
3 生产线建模与仿真试验
3.1 建模
建模是对研究系统模型化的过程,通过建模得到系统模型,模型是对实际系统本质的抽象描述,能够反映实际系统的特征。仿真是建立实际系统模型并对其进行试验研究从而认识实际系统的过程。
按照仿真流程[9],运用仿真软Plant Simulation建立生产线仿真模型[10],如图2 所示。

图2 生产线仿真模型
3.2 试验设计
全因子设计是试验设计的方法之一,其将不同水平下的各试验因子进行组合生成采样点,具有较高的建模精度,但试验时间较长,适用于因素数与水平数较少的情况[11]。
将AGV 的数量、配送量及速度作为输入变量,将产线生产周期、暂存区总容量、设备平均利用率及AGV 平均利用率作为输出变量,进行全因子试验设计,其中置信度为95%,每个试验观察3 次,产线生产周期与暂存区总容量最小化,设备平均利用率与AGV 平均利用率最大化。全因子试验设计如表2 所示,共生成330 个样本点,构成包括各因子、各水平的样本空间。

表2 全因子试验设计表
通过试验设计,运行仿真试验,研究各因子在不同水平下的组合方式对输出变量的影响及其变化规律,仿真试验结果如图3 所示。各输出变量的统计图可分为5 个区域,对应x1的5 个水平;每个区域又可分为6 个子区域,对应x2的6 个水平;每个子区域包括11 个仿真试验结果,对应x3的11 个水平。
由图3a 可知,在AGV 数量x1、AGV 配送量x2、AGV 速度x3均变化的情况下,生产周期有先显著缩短而后缓慢增加的趋势并呈周期性变化,但是各周期性变化差异不显著,说明AGV 速度x3在一定范围内对生产周期影响较大,并且存在变量x2、x3的最佳组合使生产周期最短;同时AGV 数量x1在取值范围内对缩短生产周期影响较小。
由图3b 可知,在AGV 数量x1、AGV 配送量x2、AGV 速度x3均变化的情况下,暂存区总容量出现先显著增加再减少的趋势并呈周期性变化,但是暂存区总容量各周期性变化差异不显著,说明随着AGV 速度x3逐渐增加会促进物料流动,使暂存区总容量有减少的趋势;AGV 配送量x2增加会使暂存区总容量增加,而AGV 配送次数会减少,从而降低AGV 利用率;同时AGV 数量x1在取值范围内对减少暂存区总容量影响较小。
由图3c 可知,在AGV 数量x1、AGV 配送量x2、AGV 速度x3均变化的情况下,设备平均利用率呈下降趋势并周期性变化同时局部有周期性先上升而后下降的情况,但是设备平均利用率周期性变化差异不显著,说明AGV 速度x3增加使产线物料流动速度增加,设备处于等待状态的时间减少,设备平均利用率逐渐增加,产线生产周期相应缩短;AGV 配送量x2逐渐增加会使单位配送数量的产品批生产时间增加,导致下工位处于等待状态,从而降低设备平均利用率,x3对设备平均利用率的影响弱于x2对设备平均利用率的影响;同时AGV 数量x1在取值范围内对设备平均利用率影响较小。
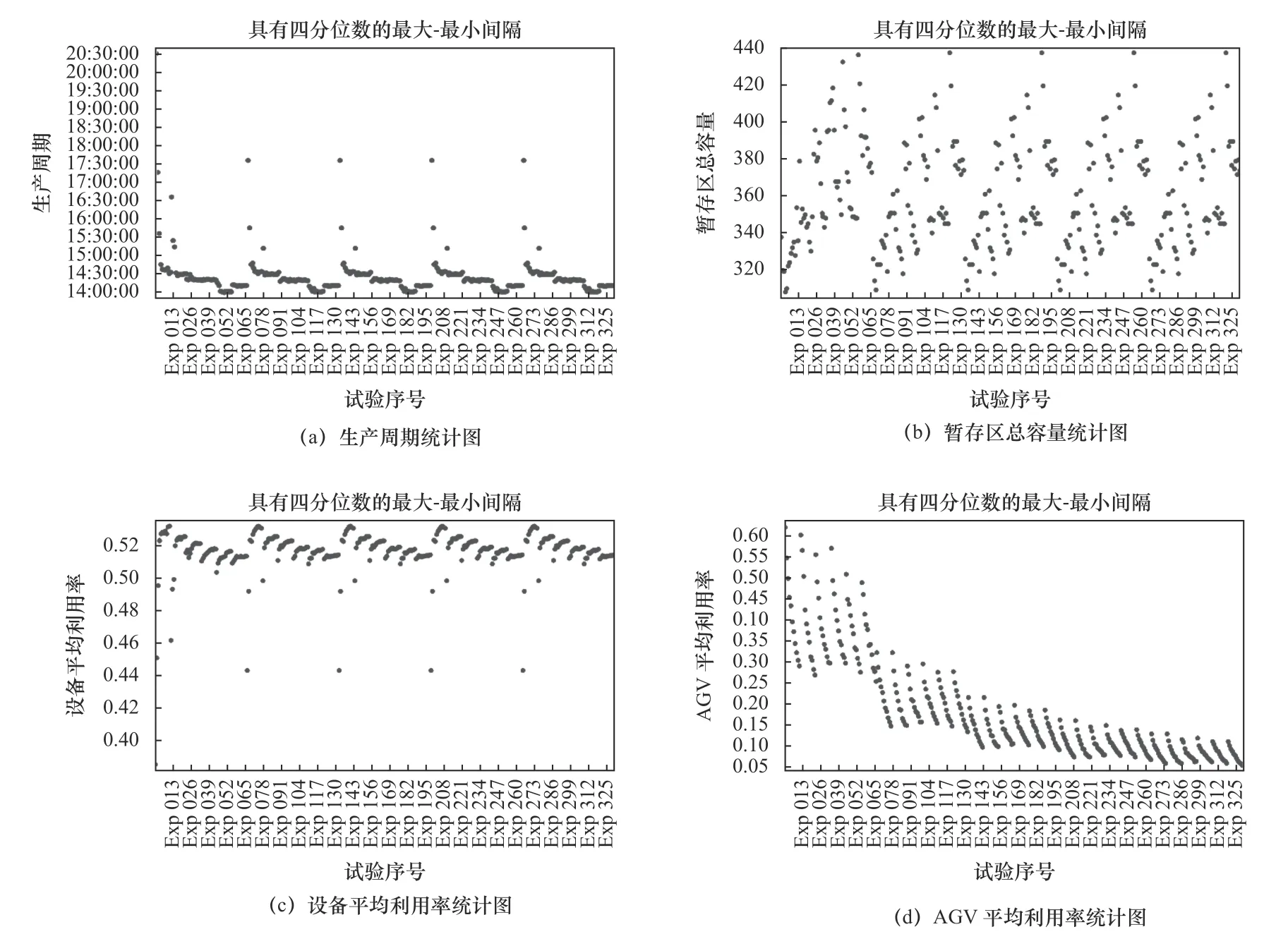
图3 输出变量统计图
由图3d 可知,在AGV 数量x1、AGV 配送量x2、AGV 速度x3均变化的情况下,AGV 平均利用率呈下降趋势,说明随着AGV 速度x3逐渐增加,AGV平均利用率下降明显;AGV 配送量x2越大AGV 配送次数越少,AGV 平均利用率降低,并且会使工位造成堵塞,降低设备利用率[12];同时AGV 数量x1在取值范围内对AGV 平均利用率有较大影响。
由试验结果可得各因子的最佳组合对应的各输出变量的最佳值如表3 所示,其中产线生产周期Y1、暂存区总容量Y2、设备平均利用率Y3、AGV 平均利用率Y4。

表3 最佳输出变量
通过分析可知,在一定范围内,AGV 数量x1对产线生产周期、暂存区总容量和设备平均利用率目标的影响不显著;AGV 数量x1对AGV 平均利用率目标影响显著,但AGV 平均利用率最佳为57.2%,处于中等负荷状态。因此,产线运行时配置1 辆AGV 作业。
设备平均利用率越高,能够反映产线运行效率越高,产线生产周期越短;AGV 平均利用率越高,能够反映暂存区总容量越小。因此,多个目标可以减少至2 个目标,即目标为设备平均利用率、AGV平均利用率。
4 遗传算法多目标优化
4.1 建立数学模型
将设备平均利用率Y3、AGV 平均利用率Y4作为优化目标,因式取值范围如表4 所示。

表4 因子取值范围
(1)优化目标1:设备平均利用率Y3
在生产线运行过程中,设备平均工作时间越长及完成的作业任务越多,设备平均利用率越高,则

式中:Bj为第j台设备的利用率,j=1,2,···,m;M为设备数量。
(2)优化目标2:AGV 平均利用率Y4
AGV 负责将物料准时运输到指定工位,使生产线中的物料顺畅流动,AGV 平均利用率越高,说明每辆AGV 作业时间越长或任务越多,则
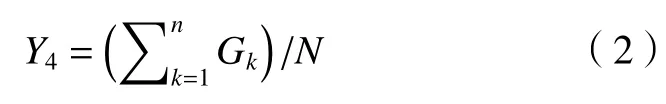
式中:Gk为第k辆AGV的利用率,k=1,2,···,n;N为AGV 数量。
4.2 遗传算法多目标优化
遗传算法(genetic algorithm,GA)具有全局寻优能力强、求解速度快等特点[13],广泛应用于全局及多目标等的约束优化[14]。因此,采用遗传算法求解问题。
将多个目标函数转化为适应度函数[15],则
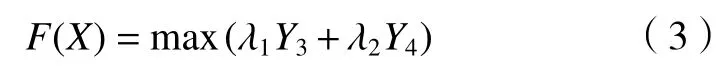
式中:λ1、λ2为权重系数,根据对优化目标的侧重不同[16],取λ1=0.6、λ2=0.4。
将数学模型编译为程序,优化方向设置为最大化,遗传代数为20,种群大小为50,经多次优化,各因子优化结果分别为x2=5、x3=1;最佳适应度值为0.476,如图4 所示。

图4 遗传算法迭代图
5 仿真验证及二次优化
5.1 仿真验证
遗传算法在优化过程中以适应度函数值作为评价群体中个体优劣的指标,考虑到整体性能最优。通过遗传算法优化,获得多目标最优解,而非单目标最优解。
将AGV 的数量x1、配送量x2、速度x3的优化结果输入到生产线仿真模型中,经多次仿真验证,仿真结果如表5 所示。在AGV 数量为1 辆,配送量为5 个产品,速度为1 m/s 的情况下,产线生产周期为52 642 s,暂存区总容量为322 个产品,设备平均利用率为52.8%,AGV 平均利用率为39.7%。各工位资源统计如图5 所示,其中工位1(M1)、工位2(M2)、工位3(M3-M6)、工位4(M7)、工位5(M8)、工位6(M9)、工位7(M10)、工位8(M11-M14)、工位9(M15-M22)及工位10(M23)。工位9 资源利用率最高为93.34%,主要为机器作业;工位3 资源利用率最低为10.58%,主要为人工作业;工位8 资源利用率为37.31%;工位2、工位8 易出现堵塞,堵塞率分别为4.94%、7.53%。
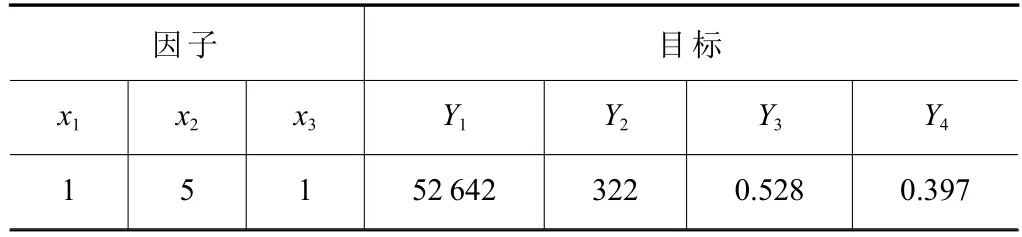
表5 多目标最优解
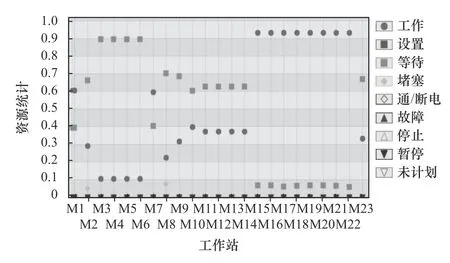
图5 工位资源统计
5.2 二次优化
通过工位资源统计可知,部分工位存在并行工序,降低了资源利用率。因此,将工位3 的M5、M6 两个并行工序及工位8 的M12、M14 两个并行工序取消,之后进行仿真验证,结果如图6、表6所示。其中,二次优化后工位3 资源利用率为21.1%;工位8 资源利用率为74.46%,如图6 所示,但是这些并行工序为人工作业,作业强度会影响作业效率,工序数量需要根据实际情况合理调整。同时,二次优化后,产线生产周期为52 805 s,增加0.3%;暂存区总容量为333 支线圈,增加3.4%;设备平均利用率为52.7%;AGV 平均利用率为40.2%。
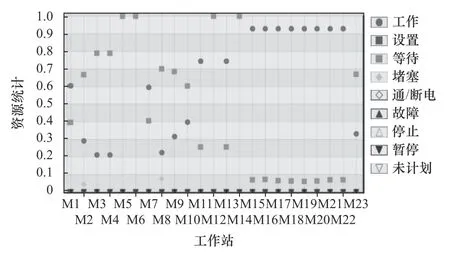
图6 工位资源统计

表6 二次优化与遗传算法优化
6 结语
(1)在产线规划设计阶段,通过仿真试验设计,探究了AGV 的数量、配送量及速度与多个目标之间的影响,确定关键因子与优化目标,该方法能够有效降低求解问题的复杂程度及设计工作量。
(2)在满足约束条件下,运用遗传算法求解,使设备平均利用率与AGV 平均利用率目标最大化,获得多目标最优解,该方法有效平衡了多目标之间的制约影响,优化解达到预期目的。
(3)在遗传算法优化基础上,通过对减少并行工序数量进行仿真研究,结果表明在满足约束条件下,减少并行工序数量能够提高资源利用率。由于人工作业受到作业环境及作业强度的影响,需要根据情况进行并行工序数量的调整。
