考虑温度影响的机床螺栓结构接触特性分析＊

雷 声 毛宽民 李 明 赵飞宇

（①中南民族大学计算机科学学院，湖北 武汉 430074；②华中科技大学机械科学与工程学院，湖北 武汉 430074）

螺栓结连接结构广泛用于机械系统的连接中，其连接特性对机械系统的整体动力学特性有着显著的影响。以机床结构为例，研究表明，机床50%以上的刚度来自于连接部分[1]。目前常用的结合部模型主要有弹簧模型[2-3]、薄层单元模型[4]、等效梁模型[5]，虚拟材料模型[6]等。螺栓结合面的动力学特性主要取决于接触面内的接触情况，而结合面内的接触情况与诸多因素有关。建立实用的结合部模型参数库，是结合部模型迈向工程应用的重要一步。黄小磊等[7]在分析连接结构尺寸、螺栓的直径和预紧力等因素的影响基础上，建立了八节点六面体模型的参数库。毛宽民团队[8]采用虚拟材料模型，建立了不同连接参数下的虚拟材料模型的参数库。相关研究为结合部模型的应用提供了有效的途径。

然而，这些研究均没有考虑温度变化对连接部分接触特性的影响。一方面，机械结构的环境温度受到昼夜性及季节性变化的影响，如机床的环境温度变化可达20 ℃；另一方面，部分机构工作状态与非工作状态下的温度差异非常大，如发动机燃烧室工作时温度高达1 800 ℃[9]，发动机螺栓连接的法兰面处的温度可达800～900 ℃[10]。对于这些含螺栓连接的结构，温度的变化会对结构的接触特性产生影响，从而影响结构的整体机械机构的动力学特性。因此，研究并获得温度变化对螺栓连接结构接触特性的影响，既是建立准确的螺栓结构动力学模型的需要，也对考虑环境及工作温度变化情况下的含螺栓连接机器的动态特性检测与故障诊断有较为重要的意义。

本文首先基于ANSYS 建立螺栓连接结构接触模型；然后采用MATLAB 提取接触分析结果，在此基础上分析温度对螺栓连接结构接触区域及接触应力的影响；并以机床中常用铸铁材料为例，依次研究连接板厚、螺栓直径、螺栓预紧力等螺栓连接参数与温度耦合情况下的接触特性变化规律；最后，采用克里金插值法，构建考虑温度影响的螺栓接触特性参数模库，为考虑温度影响的螺栓结合部动力学建模提供支撑。

1 温度影响螺栓连接结构接触特性的理论基础

对于螺栓连接结构，拧紧螺母时会使得螺栓杆拉伸变长，由于螺母和螺栓头限制了螺栓杆的回缩，从而在螺栓杆上产生一定的预紧力。螺栓连接正是通过螺栓的预紧力使得两个构件连接在一起。当温度发生变化后，整体结构在温度的作用下产生相应的热变形。螺栓杆和被连接件热伸缩系数不同，导致其热变形量产生差异，从而使得螺栓杆的实际伸缩量发生变化。不同温度状态下的螺栓连接结构受力状态及变化如图1 所示。

图1 温度变化时的螺栓连接状态变化情况

根据材料力学基本理论，弹性范围内伸缩量Δδ变化与拉伸应力变化值 ΔF之间的关系如下

式中：l为连接受力部分的长度；E和A分别为材料的弹性模量和横截面积。

螺栓伸缩量的变化导致螺栓连接的预紧力产生变化，从而改变接触面内的应力大小及分布情况，进而对结构的连接特性产生影响。

2 考虑温度影响的螺栓连接结构有限元建模方法

建立考虑温度影响的螺栓连接结构的有限元模型是分析温度对结构接触特性影响的基础。以下从连接结构的建模、接触分析及结果提取3 个方面进行描述。

2.1 螺栓连接结构有限元建模

螺栓连接结构的实际接触面积及接触面内的应力分布情况决定接触部分的力学性能。考虑到螺栓结构连接部分的轴对称性，其接触应力沿着轴向的圆周分布相同，因此，需重点研究径向接触应力的变化情况。由于接触分析计算比较耗时，为了节约计算资源，在网格划分时，尽量减少径向（R）的网格尺寸，以尽可能多增加径向的节点，以便获更准确的径向接触应力分布情况；在保证雅克比矩阵的同时，适当增大单元的周向尺寸。建立的螺栓连接结构的有限元分析模型如图2 所示。

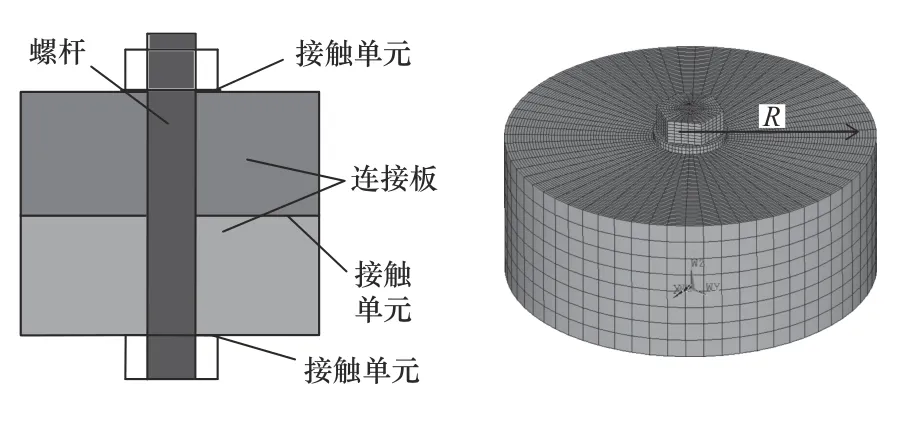
图2 螺栓连接结构的有限元模型

在建模过程中，将螺栓头与连接板、连接板之间、螺母与连接板之间添加接触单元。连接板的材料采用铸铁，螺栓的材料为碳钢，分别赋予连接板和螺栓材料参数和温度伸缩系数。施加载荷前，首先根据预紧力矩及预紧力之间的换算关系计算螺栓的实际预紧力；然后采用PRETS179 单元模拟螺栓的预紧，通过SLOAD 添加模型的实际预紧力。

2.2 有限元分析及结果提取

在建立接触单元并添加预紧力后，可以通过接触应力分析获得结构的接触应力情况。为研究温度的影响，采用BFV 命令添加温度条件，并通过载荷步分析不同温度情况下的接触应力情况。

采用PRNSOL 命令输出接触面内的接触应力情况。为便于分析对比，选择沿径向方向上的接触单元并输出其接触应力。将不同温度差的计算数据导出，保存在不同的txt 文档中。采用MATLAB 读取分析计算的不同温度差下的接触应力。

2.3 螺栓连接结构接触特性分析

为验证有限元模型的有效性，构建连接板厚为20 mm，螺栓直径为M12，螺栓预紧力矩为60 N·m的螺栓连接结构，进行接触特性分析。具体的建模及分析计算流程如图3 所示。

图3 接触分析的基本流程

采用MATLAB 绘制螺栓连接结构接触特性曲线，其结果如图4 所示。

图4 螺栓结合部接触特性分析

根据理论分析，采用压力测试纸测试螺栓连接结构接触面内的接触应力分布情况，实验测试结果如图5 所示。图中颜色的深浅表征接触应力的大小。

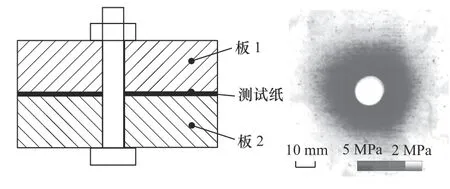
图5 螺栓结合部接触应力测试

通过理论分析计算及实验测试数据可以看出，螺栓的作用具有很强的局部效应，接触应力随着影响区域半径的增大而逐渐减弱。因此，在建立精确的螺栓连接结构的动力学分析模型时，需要考虑连接结构的局部特性的影响。

3 不同连接条件下温度影响特性分析

3.1 温度对接触特性的影响分析

为分析温度对接触特性的影响，构建连接板板厚为30 mm，螺栓直径为M12，螺栓预紧力矩为60 N·m 的螺栓连接结构。以10 ℃为温度变化步长，分析温度在0～30 ℃变化时的7 组工况下，螺栓连接结构的接触特性。采用MATLAB 绘制不同温度变化下的螺栓连接结构接触特性曲线，其结果如图6 所示。

图6 温度对接触特性的影响

通过分析计算数据可以看出，温度变化不仅影响接触面内的接触应力，同时影响实际接触区域的大小，尤其是对接触区域的边界附近的接触应力影响最为显著。其原因在于温度变化引起的热变形在边界处最为明显，因此，精确的动力学建模需考虑温度变化对连接结构接触边界处的影响。

为定量分析温度变化对接触半径及接触面内的平均接触应力的影响，首先读取接触面内的实际接触区域；然后沿着径向方向积分计算结合面内的总接触应力；最后除以实际接触面积计算平均接触应力。采用MATLAB 分析计算结果如表1 所示。

表1 温度对接触特性的影响分析

从表1 可以看出，温度的升高会使得接触面的平均接触应力增大，同时会使得实际的接触面积减小。当温差达到30 ℃时，实际接触半径减小13.02%，但接触面内的平均应力增大23.12%。

螺栓连接结构的接触特性与连接板厚、螺栓预紧力矩、螺栓直径等连接参数均密切相关。为进一步探究考虑温度影响下的接触特性，依次分析不同板厚、螺栓预紧力矩、螺栓直径这些连接参数下，温度变化对接触特性的影响。

3.2 连接板厚度与温度对接触特性的影响

以M12 的螺栓受60 N·m 力矩为例，采用ANSYS建立的有限元分析模型，分析不同板厚下温度对结合部接触特性的影响，以10 mm、20 mm、30 mm和40 mm 这4 组板厚为分析对象。采用MATLAB提取ANSYS 分析获得的连接表面的接触应力，绘制不同板厚情况下的接触特性曲线如图7 所示。

图7 不同板厚下温度对接触特性的影响

为定量研究板厚变化与温度的耦合影响，分析温差30 ℃时不同板厚下的接触半径及接触应力的变化情况，计算结果如表2 所示。

表2 不同板厚的接触特性（温差30 ℃）

通过分析不同板厚下的接触特性曲线发现，不同板厚情况下，温度对结合部接触特性的影响具有相似的规律，温度的升高会使得结合部的平均接触应力增大，同时会使得实际的接触面积减小。当实际板厚比较小时，螺栓的作用区域很有限，此时温度变化对结合部的影响并不突出，但当板厚增大到一定值后，温度的影响就比较显著。因此，对于厚板连接的螺栓结构，其力学建模及分析时需要考虑温度变化的影响。

3.3 螺栓直径与温度对接触特性的影响

为分析不同螺栓直径下温度对接触特性的影响，以M12、M16 及M20 三组螺栓为分析对象，分析计算不同螺栓直径情况下的接触特性曲线。需要说明的是，由于相同预紧力矩下的不同直径螺栓的预紧力不同，不同直径的螺栓结构接触分析中需保持螺栓的预紧力不变。因此，仿真分析时，对M12、M16 和M20 的螺栓分别施加60 N·m、80 N·m 及100 N·m 的预紧力矩，以保持三组直径下的螺栓的预紧力相同。计算结果如图8 所示。在保持预紧力不变的情况下，螺栓直径的变化对接触面积及接触面内的压力的影响很小。仿真结果也验证了接触面内的压力来源于螺栓的预紧力这一事实。

图8 不同螺栓直径下温度对接触特性的影响

3.4 螺栓预紧力与温度对接触特性的影响

为分析不同预紧力下温度对接触特性的影响，以M12 螺栓受30 N·m、60 N·m、90 N·m 及120 N·m四组预紧力矩为分析对象，对应的预紧力分别为12 500 N、25 000 N、37 500 N 以及50 000 N。计算不同螺栓预紧力情况下的接触特性曲线，结果如图9 所示。

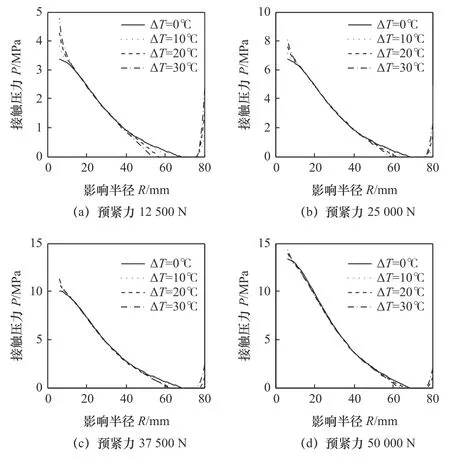
图9 不同预紧力下温度对接触特性的影响

为定量研究板预紧力变化与温度的耦合影响，分析温差为30 ℃时不同预紧力下的接触半径及接触应力的变化情况，结果如表3 所示。

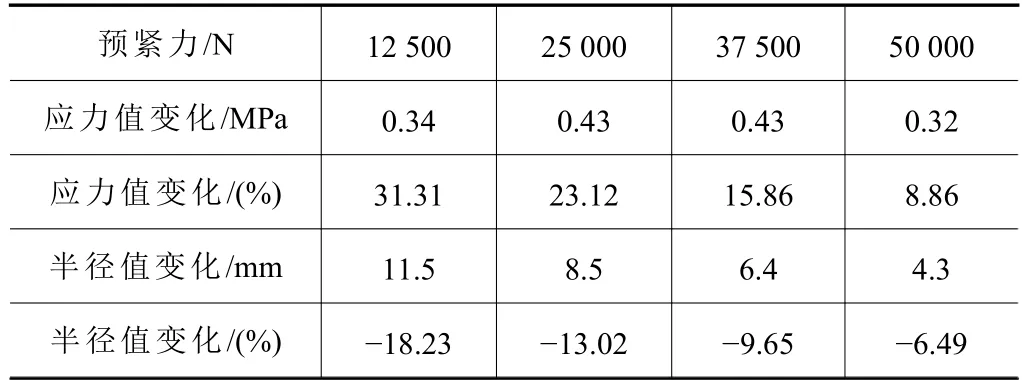
表3 不同预紧力时的接触特性（温差30 ℃）

由图9 及表3 可知，平均接触应力值随着预紧力的增大而显著增大，但平均接触面应力值的变化随着预紧力的变化并不明显。实际接触区域随着预紧力的增大变化不显著，但实际接触区域的变化随着预紧力的增加而减少。分析结果表明，当预紧力较小时，温度变化会较为显著地影响接触面积和平均接触应力；但当预紧力较大时，温度变化对接触面积及平均接触应力的影响并不明显。

4 考虑温度影响的接触模型参数库构建

应用螺栓结合部模型参数库时，首先需要获得螺栓连接结构的实际接触区域的大小及接触面内的平均应力，而目前建立的参数库均未考虑温度变化的影响。通过第3 节分析可知，由于温度与板厚、预紧力的耦合作用，温度变化会影响接触半径及接触面平均接触应力，从而影响机床结构的动力学特性。因此，本节采用克里金插值法，构建考虑温度影响的螺栓连接结构动力学模型参数库。

4.1 克里金插值法的基本原理

克里金法是建立在变异函数理论分析基础上的一种空间局部内插法，假设响应值由回归模型g(t)和随机过程函数Z(t)组成

其中：回归模型g(t)根据实测数据的特性选定，Z(t)是均值为0 而协方差非零的随机过程函数，在所有样本点处的误差为0。在待估计点t0处的函数值可以表示为

式中：ti(i=1,2,···,n)表示已知的样本点；z(ti)表示已知的样本点的值；λi为待定的权系数，其数值由下式计算

依据克里金法建立的响应变量和输入变量之间的统计模型，计算出权系数之后，可以分析和预测输入变量对响应结果的影响。

4.2 克里金模型的构建

由于螺栓连接结构的实际接触区域有局部特性，通过全面仿真分析，计算板厚为10 mm、20 mm、30 mm 及40 mm 时，预紧力为12 500 N、25 000 N、37 500 N 及50 000 N 时，温度变化为0 ℃、5 ℃、10 ℃、15 ℃、20 ℃、25 ℃及30 ℃时的接触面积及接触面压力，获得16 组不同连接工况在7 种温度变化情况下的接触特性数据。分析获得的112 组平均接触应力数据及接触影响区域半径数据如表4和表5 所示。

表4 不同连接工况下的平均接触应力

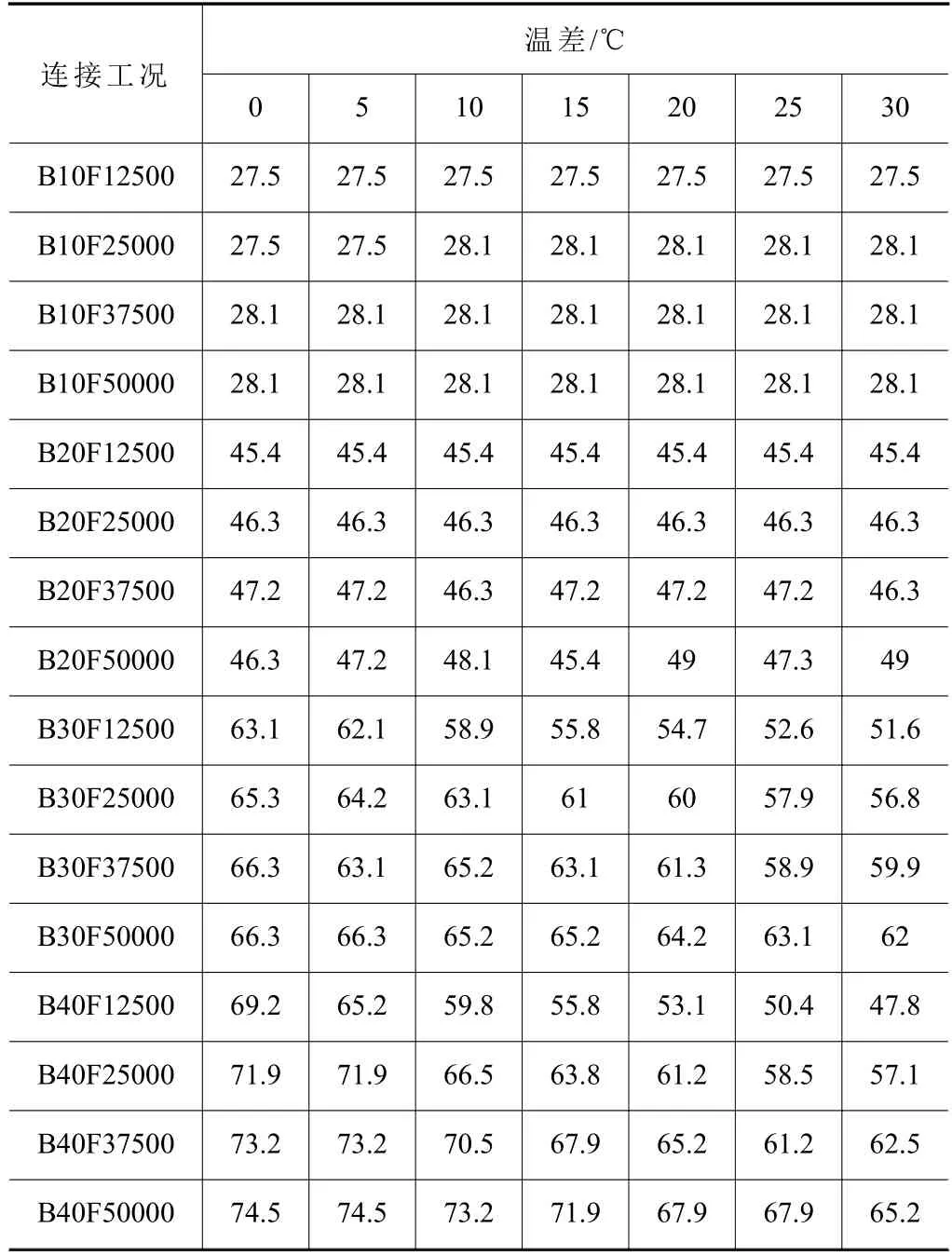
表5 不同连接工况下的平均接触半径

以不同板厚、预紧力及不同温差下的112 组数据为输入变量，以分析获得的112 组平均接触应力及平均接触半径数据为响应值，基于克里金插值法，采用MATLAB 中的dacefit 函数构建响应值和输入变量之间的统计模型，由此构建考虑温度影响的螺栓连接结构接触模型参数库。

4.3 模型参数管理库的开发

为了方便工程应用，采用MATLAB 的GUI 开发环境建立参数管理库。需要说明的是，在工程应用中，习惯采用螺栓的直径和预紧力矩作为螺栓连接的主要描述方式，而螺栓的预紧力与螺栓直径及预紧力矩之间存在转换关系。为了更加方便地将所建立的模型应用于动力学建模及分析之中，在建立参数管理库时，将螺栓的直径和预紧力矩一起作为输入参数，开发的数据图界面如图10 所示。

图10 接触特性参数管理库

用户根据GUI 界面的提示，输入螺栓连接相应的参数后，程序首先通过预紧力矩、螺栓直径及预紧力之间的关系，计算出螺栓连接结构的预紧力，然后再结合连接板厚及温度，采用克里金模型计算影响区域面积及接触面内的平均接触应力，并通过管理界面输出，供用户使用。

5 结语

本文建立了螺栓连接结构的有限元模型，并分析温度对螺栓连接结构接触特性的影响，主要工作如下：

（1）温度变化不仅影响螺栓连接结构接触面内的接触应力值，也影响连接结构的实际接触区域的大小。对于铸铁连接机构，温度的升高会使得螺栓结合部的平均接触应力增大，同时会使得实际的接触面积减小。在整个接触面内，温度对接触区域边界处应力分布的影响最为显著。

（2）板厚比较小时，温度变化对接触特性影响并不显著；但当板厚增大到一定程度后，温度变化会使得接触区域的变化及接触应力的变化显著增大。

（3）预紧力对螺栓连接结构的接触特性有显著影响，当螺栓连接结构的预紧力相同时，螺栓直径变化对接触面的影响很弱。预紧力较小时，温度变化会较为显著地影响接触区域大小和平均接触应力；但当预紧力增大到一定程度后，温度变化对接触区域大小及平均接触应力的影响并不明显。

（4）采用克里金内插法，建立了考虑温度影响的螺栓连接结构接触模型参数库，并基于MATLAB开发了数据库的管理系统，为考虑温度影响螺栓结合部动力学建模提供了基础支撑。