螺栓预紧的有限元分析及计算

董 超，陈福建，刘 刃，孙红梅，孙成丽

（济南二机床集团有限公司，山东 济南 250022）

在机械联接结构中，螺栓联接由于具有结构简单、拆卸方便、标准化等优点而得到广泛应用。为保证其联接可靠性，通过对螺栓联接施加预紧扭矩从而产生预紧力将螺纹拧紧是最常用的预紧方法。但预紧扭矩的大小需适当控制，过大的扭矩会增大螺栓的应力，过小的扭矩则会降低螺栓联接的可靠性。

为方便通过理论计算对螺栓预紧有限元分析结果进行验证，本文针对承受轴向力的单个螺栓联接进行分析，联接由一个螺栓、一个螺母、两个套筒组成。螺栓螺纹规格为M20×2.5，材料为碳钢，强度等级为6.8级。两个套筒的尺寸相同，内径为22，外径为40，高度为50，材料为45钢。

对于一般联接用的螺栓联接的预紧力F0，可按下列关系确定[1]：

式中：σS——螺栓材料的屈服极限；

A1——螺栓危险截面的面积。

1 螺栓预紧的有限元分析

利用NX软件建立假定的承受预紧力与轴向工作力的螺栓连接的三维模型。将该模型进行静力分析，为螺栓预紧及强度校核提供数据支持。本文建立的螺栓连接三维模型如图1所示。

1.1 计算两个套筒的组合刚度

由式（1）可知，对于碳素钢螺栓，预紧力系数可取0.6，对于6.8级强度的螺栓，其屈服强度为480MPa，危险截面为小径d1（17.294mm），经计算预紧力大小67651N。对于M10～M64的粗牙普通螺纹钢制螺栓[1]，预紧扭矩等于预紧力与螺栓公称直径乘积的0.2倍，经计算得预紧扭矩271Nm。在分析模型中，预紧力施加在螺栓长度的中间截面上[2]，摩擦系数0.15。分析模型中钢的弹性模量206GPa，泊松比0.3。套筒轴向组合刚度的有限元分析模型如图2。

图1 螺栓连接三维模型

图2 套筒组合刚度的分析模型

经有限元计算，套筒两端轴向变形如图3所示。

由图3可知，套筒两端的相对轴向变形为ΔL=0.010-（-0.028）=0.038 mm，套筒的组合轴向刚度为：

1.2 计算螺栓的刚度

若手工计算螺栓的轴向刚度，则对于螺栓头及螺母的影响无法准确考虑，因此采用有限元计算螺栓的刚度是比较准确的，在螺栓头及螺母内侧端面分别施加67651N的均布载荷，分析模型如图4所示。

经有限元计算，螺栓两端的轴向变形如图5。

图3 套筒两端轴向变形

图4 螺栓刚度的分析模型

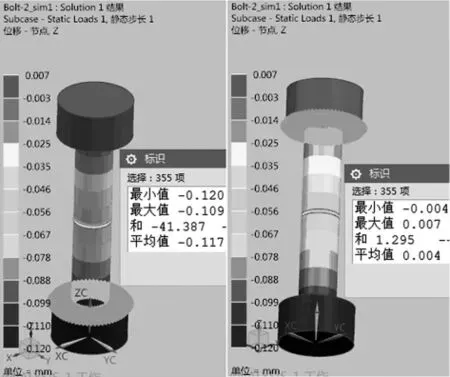
图5 螺栓两端轴向变形

由图5可知，螺栓两端的相对轴向变形为ΔL=0.004-（-0.117）=0.121mm，螺栓的轴向刚度为：

1.3 计算螺栓工作时的应力

假定螺栓承受的轴向工作力F为10000N，螺栓在预紧力与工作力共同作用下的分析模型如图6。

图6 螺栓承受轴向工作力的分析模型

由于螺栓中间截面施加了预紧力，而螺栓头与螺母位置的应力受到接触变形的影响，为了便于通过手动计算校核应力分析结果，因此在距离螺母内侧端面25mm（套筒的中间位置）的位置截取螺栓横截面的等效应力，结果如图7所示。

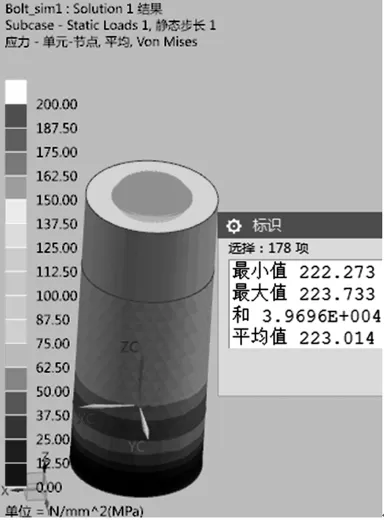
图7 螺栓横截面等效应力

由图7可知，选定的螺栓横截面上的平均等效应力σ1为223.014MPa。

根据机械设计教材中计算螺栓总拉力的计算公式，得总拉力为：

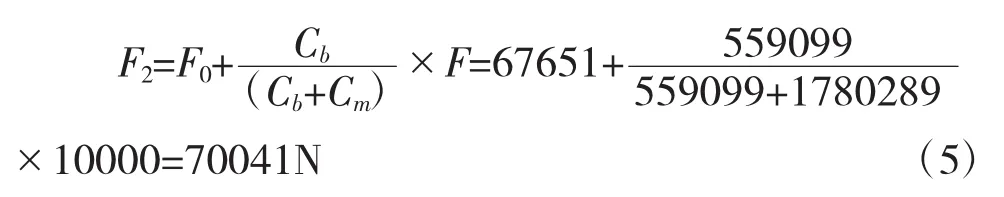
螺栓的横截面积为：

螺栓的横截面平均计算拉应力为：

有限元计算应力与理论计算应力的相对误差为：

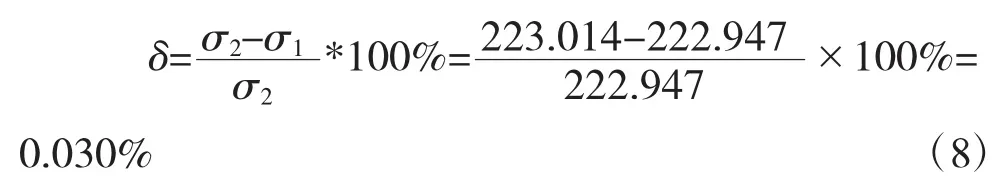
由式（8）可知，有限元计算的螺栓应力结果是比较准确的。

2 螺栓残余预紧力的计算

由机械设计教材可知，螺栓承受轴向工作力时的力与变形的关系如图8所示。

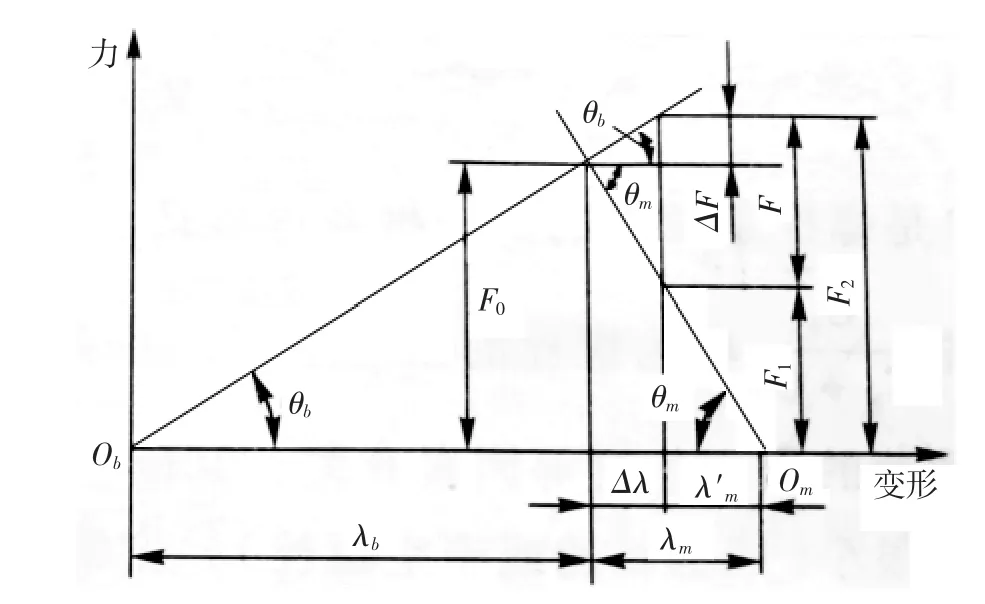
图8 螺栓受力与变形的关系

由图8可知，螺栓的残余预紧力为：

由式（9）可知，残余预紧力比工作力10000N大，该螺栓连接可用于不稳定的工作载荷。

3 螺栓强度的校核

由机械设计教材可知，校核螺栓静强度时，若考虑扭转切应力的影响，则需要将螺栓总拉力增加30%，故该螺栓危险截面的拉伸应力为：

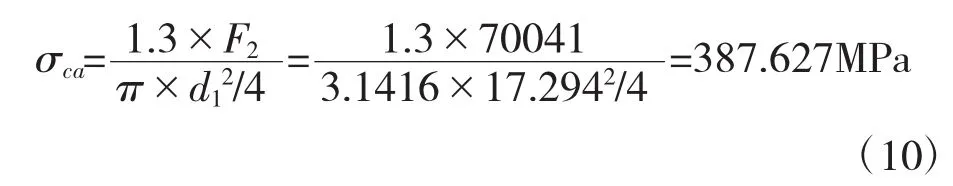
对于静强度校核[3]，安全系数可取为1.2，则许用强度为：

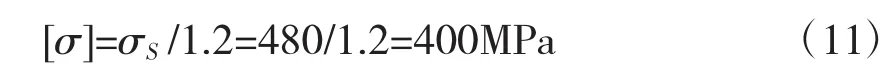
由于σca＜[σ]，因此螺栓静强度满足强度要求。对于螺栓疲劳强度，由于影响因素较多且与实际结构尺寸及加工精度等密切相关，本文不再讨论。

4 结论

本文对承受预紧力和轴向工作力的单个螺栓连接进行了有限元分析，通过理论计算对螺栓横截面平均应力的有限元分析结果进行了验证，并对残余预紧力与静强度进行了校核。螺栓连接作为重要的机械连接，其计算是很关键的，对于承受复杂载荷的螺栓组连接，利用有限元分析进行计算具有明显的优势，螺栓连接的精确计算需要将相关理论与有限元相结合才能获得比较理想的结果。