考虑行波效应的钢管混凝土拱桥地震响应分析

贾文涛， 马博男

(西南交通大学土木工程学院，四川成都 610031)

地震波的易变性通常是指地震波的振幅、相位及频谱特性随时间和空间的变化而变化，具体表现为部分相干效应、行波效应和局部场地效应。既有研究表明[1-4]，地震动的空间易变性对于大跨度桥梁的地震响应影响较大，其中由于地震波沿桥纵向到达先后的时间差所引起各支承处地震时程的相位差从而产生的行波效应对大跨度桥梁结构地震响应的影响起主导作用。钢管混凝土拱桥作为近几年来应用广泛的桥型之一，其设计理论及施工技术也逐渐完善。但随着跨径的增加，钢管混凝土拱桥抗震性能的问题也日益突出，因此钢管混凝土劲性骨架拱桥作为大跨度新型桥梁，有必要对其进行非一致激励分析以考虑行波效应的影响。

近年来，针对多点激励作用下大跨度钢管混凝土拱桥的地震响应，国内外学者进行了诸多研究。吴玉华等[5]采用大质量法对钢管混凝土拱桥进行了三维正交地震动多点激励下的地震响应分析并考虑了几何非线性，结果表明行波效应可以显著增大拱肋的内力，其影响不容忽视。陶哲等[6]通过对钢管混凝土拱桥输入三维地震动并取不同的视波速以研究行波效应对地震响应的影响，结果表明在不同视波速的三维地震激励响应下行波效应对结构地震响应的影响也不同，在抗震设计时对行波效应视波速的取值应进行专项研究。刘珍[7]采用动态时程分析法对大跨钢管混凝土拱桥的行波效应进行了研究，结果表明考虑行波效应后拱桥结构各关键截面处的纵向位移及内力均有显著增大，进行抗震设计时有必要考虑行波效应。

本文以郑州至万州某主跨为340 m上承式铁路劲性骨架混凝土拱桥为工程背景，采用Midas Civil建立有限元模型，考虑了结构的桩-土相互作用，通过大质量法实现多点激励，基于非线性时程分析方法研究了行波效应对大跨钢管混凝土劲性骨架拱桥地震响应的影响。

1 计算条件

1.1 桥梁概况

以郑州至万州铁路某钢管混凝土劲性骨架拱桥为工程背景，主桥为340 m上承式劲性骨架钢管混凝土拱桥，本桥桥址区场地类别属II类，设计地震分组为1组，抗震设防烈度为VI度，地震动反应谱特征周期0.35 s，罕遇地震作用下水平地震基本地震动峰值加速度为0.11g。主梁采用预应力混凝土连续梁，主拱圈采用顶部合并的提篮形双肋式，计算跨径为340 m，竖直平面内矢高为74 m，矢跨比为1/4.595，拱轴线采用m=3.2的悬链线。拱肋在拱脚处为单箱单室截面，在拱顶合并处为单箱三室截面，拱肋中心距为20 m，主拱肋箱体采用钢筋混凝土矩形截面，纵向变高度，拱箱外缘高度由拱脚处11 m变至拱顶处6 m，按1.5次抛物线变化。主拱肋劲性骨架上下弦杆采用钢管混凝土构件，上下弦主钢管共计8肢，拱肋主弦管为φ750×24 mm，横梁弦管为φ560×16 mm，连接系为四肢组合角钢结构，腹杆为4L200×20 mm、上下平联为4L160×16 mm、其余连接件为4L90×12 mm。交界墩和拱上立柱均采用双柱式桥墩，单个立柱横向向内倾斜，桥型总体布置如图1所示。

图1 桥型布置(单位：m)

1.2 地震动输入

地震波选取和输入对地震响应的分析起着至关重要的作用，本文以地震动的三要素频谱特性、持续时间、有效峰值作为判断标准，为考虑地震动的随机性，根据本桥的场地特征，采用Midas Building进行选波。选取2条自然波Gpk_270w和Northridge-V以及一条人工波RH4TG025作为输入地震动，限于篇幅，仅给出Gpk_270w波的加速度及速度时程，见图2。本文所选地震波均满足地震动三要素，见表1。

表1 地震动特性值及调波系数

图2 Gpk_270w波的加速度及速度时程

通过调整系数将所选3条地震动的峰值加速度调整为0.11g并基于大质量法的α项修正[8]后作为罕遇地震输入地震波进行地震响应分析，见图3。

图3 Gpk_270w波α项修正前后速度时程对比

鉴于本文以大质量法(LMM)沿顺桥向及竖向施加地震激励，故施加的地震波以力的形式施加于桥梁基础底部的等效质量上，通过调整输入地震动的放大系数来实现由地震动加速度到地震动力的转换，竖向地震力取顺桥向地震力的0.65倍。地震波沿桥梁纵向、横向和竖向3个方向传播，但由于结构竖向和横向传播距离较小，所以本文仅考虑纵向地震波的行波效应。根据GB 50111-2006《铁路工程抗震设计规范》第4.0.1条，第II类场地的剪切波速范围为250 m/s≤Vse≤500 m/s，因此为研究行波效应对桥梁地震响应的影响，依次取250 m/s、500 m/s、1 000 m/s、1 500 m/s、2 000 m/s、2 500 m/s和无穷大(一致激励)7个地震波速进行时程分析。

2 有限元模型

2.1 主桥地震响应分析模型

采用有限软件Midas civil 2017建立全桥三维空间有限元模型，主梁、拱肋劲性骨架、交界墩及拱上立柱均采用梁单元模拟，拱肋外包混凝土采用板单元模拟。交界墩及拱上立柱与主梁采用刚性连接；拱上立柱与拱肋采用刚性连接；模型中采用土弹簧模拟桩土相互作用，其等效弹簧刚度采用m法计算，主桥有限元模型见图4。桥梁阻尼采用瑞利阻尼，即C=αM+βK(其中，α为质量因子，β为刚度因子)，结构阻尼比取0.05，计算频率分别取振型质量参与系数较大的第一阶频率0.387 Hz和第二阶频率0.537 Hz，计算得到α为0.141，β为0.017 2，二期恒载取147 kN/m。

图4 主桥有限元模型

2.2 非一致激励地震响应分析模型

在全桥动力弹塑性地震响应分析模型的基础上，采用大质量法处理模型边界并施加非一致性激励即可建立起非一致弹塑性地震响应分析模型，如图5所示。具体分析方法为：首先释放支撑节点沿地震波输入方向的约束并添加大质量块m0，大质量系数m0取结构总质量的106倍，其次在所有支撑节点处沿地震波方向施加地震力m0üg,new，其中üg,new是进行α项修正后的地震面运动加速度时程[9]。

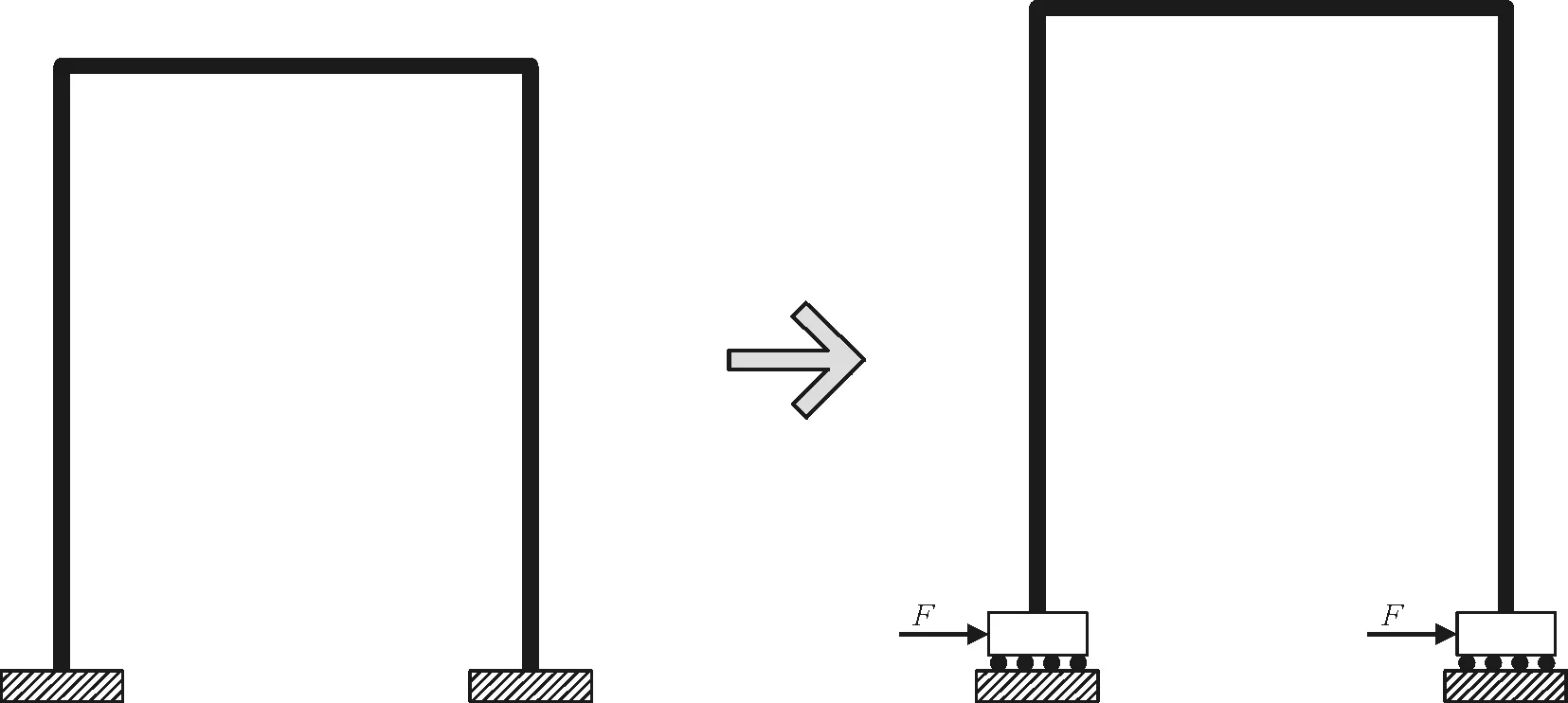
图5 非一致激励地震响应分析模型(LMM模型)

2.3 模型验算

模型建立的正确与否对分析结果起着决定性的作用，本文采用的非一致激励地震响应分析模型所建立的关键点有2点：采用梁、板单元模拟桥梁构件的准确性和采用LMM法施加非一致性激励的正确性。由于在Midas Civil软件中使用梁、板单元模拟钢管混凝土劲性骨架拱桥性能的方法已经较为成熟，因此如何判断LMM法施加地震激励的正确性成为了判断模型正确与否的关键。本文通过LMM法按照一致激励输入Gpk_270w地震波，考察各支撑节点获得的加速度响应与输入的地面加速度是否一致进行判断，如图6所示。

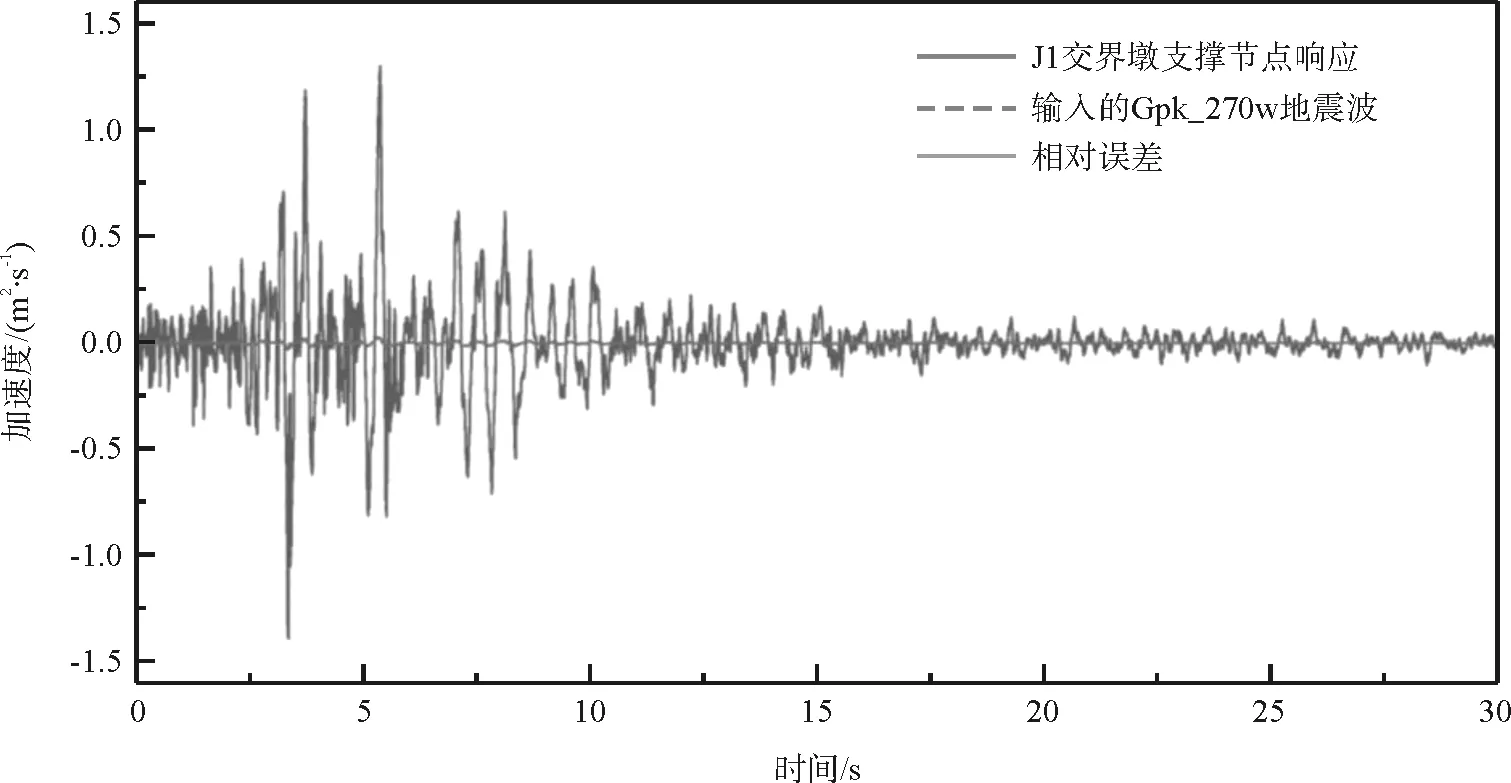
图6 加速度时程曲线对比

2.4 动力特性分析

对于本文的动力特性分析，采用多重Ritz向量法计算该桥的动力特性值。分别计算前200阶振型，并确保在X、Y、Z3个方向上的累积振型有效参与质量均大于90%，以满足抗震规范的要求。限于篇幅，本文仅给出前8阶自振特性见表2。

表2 结构自振周期及振型描述

3 行波效应的影响与分析

为研究行波效应对大跨度钢管混凝土劲性骨架拱桥内力和位移的影响，选取主拱圈拱脚、1/4跨位置、拱顶等关键截面的内力和拱顶处位移为研究对象，分别比较不同波速下非一致激励和一致激励对其内力和位移的影响，为便于比较，下文中所述结果均为所选3条地震波响应的平均值。

3.1 位移

考虑行波效应的非一致激励和一致激励作用下拱顶的位移响应如表3所示。图7为地震波速变化对拱顶位移响应的影响，其中纵坐标为考虑行波效应的非一致激励和一致激励作用下拱顶截面位移响应的比值。由图7可知：不同自由度方向位移受行波效应的影响不同，行波效应的作用下，拱顶纵向位移稍有减小，横向位移略有增大，当地震波波速为250 m/s时，纵向位移减小16%，横向位移增大29%；行波效应对竖向位移的影响较为显著，当波速为250 m/s时，竖向位移扩大为一致激励作用下的2.7倍，当波速达到1 500 m/s时，拱顶纵向和横向位移几乎不受行波效应的影响，但竖向位移依然扩大了1.5倍。

图7 拱顶纵、横及竖向位移对比

3.2 内力

地震波波速变化对拱脚处、1/4跨及拱顶位置处剪力和轴力的响应如表4所示。图8～图10为地震波波速变化对关节截面内力响应的影响，其中纵坐标为考虑行波效应的非一致激励和一致激励作用下关键截面响应的比值。

从图8～图10中可以看出：

(1)不同波速对不同截面处地震响应的影响不同，考虑行波效应主拱圈各关键截面的内力总体上比一致激励要大，当波速为250～1 000 m/s时，对拱脚截面的内力影响较大，弯矩和轴力均增加明显，最大值与一致激励作用相比增加了近450%，因此行波效应显著增大了拱脚处的内力。

表3 不同地震激励下拱顶处位移值

表4 不同地震激励下关键截面内力值

图8 拱脚处内力比

图9 1/4截面处内力比

图10 拱顶处内力比

(2)当波速为250 m/s时，拱脚截面的弯矩和轴力受行波效应的影响均增大4倍以上，而1/4截面和拱顶处弯矩和轴力仅增大1.2～3倍，这表明不同位置处内力受到行波作用的影响不同；随着波速的增大，各截面内力大多呈现先减小后增大的趋势，不同截面内力所受波速影响也不同，当波速大于2 000 m/s后，行波效应的影响很小，拱脚处弯矩和轴力值几乎与在一致激励作用下相同。

4 结论

本文通过Midas civil有限元软件对某上承式钢管混凝土劲性骨架拱桥采用非线性时程法进行了分析并对比了考虑行波效应的非一致激励和一致激励作用下大跨度钢管混凝土劲性骨架拱桥的地震响应，得到主要结论：

(1) 桥梁结构基本周期为2.583 s，柔度较大，其1阶、2阶振型为横向对称弯曲和纵飘，横向刚度最小，竖向刚度最大。

(2) 对于拱顶位移，行波效应使其纵向位移减小，横向位移和竖向位移增大，其中对竖向位移的影响最为明显。当波速达到1 000 m/s后，随着地震波波速度增大，非一致激励下的纵向和横向位移变化平缓，逐渐趋于一致激励，但竖向位移变化仍十分明显，行波效应对竖向位移的影响十分显著。

(3)主拱圈各关键截面处内力受行波效应影响十分显著，其中拱脚处内力所受影响最为明显，当地震波的波速为250 m/s时，其最大弯矩、轴力分别增大了364%和324%，弯矩提升的幅度大于轴力。在行波效应的作用下，不同波速对截面内力的影响也不尽相同，随着波速度的增大，各截面的弯矩和轴力主要呈先减小后增大的趋势，但增大趋势并不明显。

(4)对于本文所分析的钢管混凝土劲性骨架拱桥而言，行波效应会增大结构的地震响应，因此在对大跨度钢管混凝土劲性骨架拱桥设计时不可忽略行波效应的影响。