高超声速流动与换热数值仿真研究*

王 强，徐 涛，姚永涛

（1.中北大学 能源动力工程学院，太原 030051；2.特种环境复合材料技术国家级重点实验室，哈尔滨 150001）

引言

高超声速飞行器是21 世纪航空航天的一个主要发展方向，其总体技术涵盖气动力与气动热数值模拟、一体化设计、多学科优化设计、热防护与热管理技术等方面[1].气动热效应显著是高超声速飞行器的重要特征，准确预测飞行器的气动力与热载荷是进行气动设计、热防护系统设计的前提.高超声速飞行器表面通常存在缝隙，如防热瓦之间、控制舵与机体之间；由于安装、局部受热不均等影响，防热瓦之间还存在一定的阶差.在飞行过程中，高速气流会流入防热瓦缝隙中，导致防热瓦表面的流动特性与传热方式发生变化[2]，阶差使防热瓦表面的流动与换热情况进一步复杂化.此外飞行器头部一般为钝体结构，在高超声速来流作用下，局部气动热现象严重，准确预测该区域温度分布对飞行器的设计至关重要.

Hinderks 等[3]采用弱耦合方法实现了自编程序TAU 以及商业求解器ANSYS 的耦合，进行了缝隙流动、防热瓦传热以及热变形的气-热-弹耦合仿真分析，其研究揭示了缝隙内的旋涡结构，同时由于防热瓦热变形的缘故，缝隙几何形状会发生变化，进而影响缝隙内壁面的热流密度分布.应用多场耦合技术，沈淳等[4]研究了缝隙-腔体密封结构在高速气流冲击下的整体流动、传热特征；殷超等[5]采用FLUENT 商业求解器对高超声速飞行器缝隙流动传热问题开展了数值仿真，研究了不同状态参数对缝隙流动与传热的影响.邱波等[2]进行了高超声速飞行器表面横缝旋涡结构及气动热环境数值模拟，对缝隙表面热流分布、缝隙内流动状况等进行了较系统的研究.

聂涛等[6]采用有限体积法与有限元法分别求解了非定常Navier-Stokes 方程与非稳态导热方程，基于准稳态假设对固体结构问题进行了分析，实现了高超声速飞行器前缘流固耦合的计算.基于热流计算的可靠性问题，李邦明等[7]研究了高超声速飞行器前驻点热流数值模拟的物理准则.张昊元等[8]对一种开缝前缘的简化模型进行了数值仿真，研究了缝隙诱导形成的三维旋涡的空间分布特征和旋涡运动对物面气动加热的影响规律，发现缝隙内主旋涡的再附导致了侧壁存在“非常规”的高热流区.

针对高超声速流动与换热问题，本课题组基于有限差分法开发了仿真求解器，并将该求解器分别用于高超声速台阶、缝隙流动以及非定常钝体绕流与换热问题的仿真求解，分析其流动与传热特点，并对求解器的计算能力进行了验证.

1 数学物理模型

任意曲线坐标系下，引入预处理技术的守恒变量形式的无量纲Reynolds 平均Navier-Stokes（Reynolds averaged Navier-Stokes，RANS）方程为

其中Q=J·(ρ ρuρvρw e)，ρ为密度，u，v，w为速度矢量在直角坐标系下的三个分量；E，F，G和Ev，Fv，Gv分别为曲线坐标系的无黏通量与黏性通量；t为时间；ξ，η，ζ为自然曲线坐标系的坐标分量.方程中的无黏通量采用AUSM + - up 格式[9]离散，该差分格式为AUSM 类差分格式最新发展的类型，该格式在构造过程中，考虑了低Mach 数效应的影响，可以应用于全速域流动的仿真计算，具有扩展性好的优点；黏性通量采用中心差分格式离散.采用q-ω低Reynolds 数二方程模型[10]对RANS 方程进行封闭，该模型本质上是一种低Reynolds 数湍流模型，在壁面网格满足要求的条件下，不需要壁面函数，对边界层流动的预测精度较高，同时该模型对高超声速流动预测也较令人满意.采用预处理技术提高求解器对不同流域流动问题的求解能力[11]，离散后的代数方程组采用目前在计算流体力学领域广泛应用的LU-SGS 隐式方法[12]求解.

固体导热微分方程为

其中C为固体比热容，T为温度，λ为固体导热系数.由于导热的扩散性质，在计算中采用中心差分离散，并采用Douglas-Rachford（D-R）交替隐式迭代法[13]求解离散后的固体导热代数方程组.

对气热耦合仿真需要保证交接面处流固两侧壁温Tw相同，热流密度qw连续，即涉及到热流密度计算，本文采用直接耦合方法实现流体与固体交界面处的数据传递，该方法避免了热流密度qw的计算，通过流固两侧单元的温度、两侧网格单元距离交接面的距离Δn计算壁面温度，易于数据传递的实施，流固耦合交接面上温度计算如下：

非定常气热耦合计算包括流动控制方程以及固体导热方程的非定常计算，必须要考虑到流场以及固体温度场的时间同步推进.在计算中，对流动控制方程，采用双时间步法[14]实现非定常隐式求解；对非定常固体导热方程，将D-R 隐式迭代法中的时间替换成物理时间，进行显式推进；考虑到气动加热问题的强耦合属性，为了保证计算的精度，在计算中对两个物理场采用统一的物理时间步长.

在定常计算中，当参数的平均残差小于10-4或残差趋于水平后，即终止迭代；对非定常计算，当迭代物理时间达到总的物理时间后计算终止.

2 高超声速流动与换热数值仿真

2.1 高超声速后台阶流动与换热

采用与Grotowsky 与Ballmann 相同的后台阶算例[15]进行后台阶流动与传热的验证，该算例试验数据来自于Jesson 等[16]的研究，该算例文献中的模型如图1 所示.

图1 后台阶算例模型尺寸Fig.1 Geometry of the back-step model

来流条件为：Mach 数7.898，温度122.0 K，压强613 Pa，Reynolds 数3.716 × 106，攻角-15°.台阶高度H为6 mm、入口段长度L为50 mm、出口位于台阶下游120 mm 处，计算中设置为超音速出口.计算中壁面温度设置为300 K.出于对比目的，壁面第一层网格单元距离为1.0 × 10-5m，与文献[15]保持一致.网格单元数为26 496 个，与文献接近（25 836 个），计算网格如图2 所示.

图2 高超声速后台阶流动计算网格Fig.2 The computational mesh for hypersonic flow over backward facing step

图3 给出了预测的密度等值线云图，图中参数用参考值0.012 51 kg/m3进行无量纲化处理.以-15°攻角流过入口段，由于流动面积突变，在入口段最前方产生一道斜激波，气体流过斜激波，由于流动突扩，后台阶位置拐点处形成膨胀波系，同时流动分流在拐角形成漩涡流动，气流在台阶下游，x≈ 82 mm 处（文献给出的位置为81.87 mm）再附，并在该位置处产生一道再附激波.

图3 计算得到的密度等值线图Fig.3 Predicted density contours

气动力与气动热是高超声速飞行器设计的重要参数，图4、图5 分别给出了本程序预测的壁面压力与壁面热流参数，并与文献中的计算结果、试验结果进行了对比.在后台阶拐点之后，出现膨胀波系，加速流动导致局部的压强、密度等参数骤降，壁面压力值降低约70%，直到再附点附近，强压缩流动导致局部流动参数急剧提升，与再附激波前压强值相比，约增加2 倍.与压强变化相比，壁面热流密度变化具有相同的趋势，但是变化的程度更大，从试验结果来看，台阶拐点前后、再附激波前后等区域热流密度值变化均在10 倍以上.从对比结果来看，在后台阶角点之前的入口段、分离流动再附之后的区域，本程序计算的壁面压力与试验结果、文献计算结果吻合较好，误差约9.6%，在10%以内；但是台阶角点后、再附点之前的区域（50 mm ＜x＜ 80 mm）内，文献计算结果和本程序结果均与试验值存在较大的误差，该区域的预测也是目前湍流模型研究的一个难点问题，但是程序计算结果与文献结果相比，误差在10%以内.从热流分布结果来看，本程序计算的热流较文献计算结果更接近于试验结果，在50 mm ＜x＜ 80 mm 区域内，预测的热流与试验值吻合很好，误差在5%之内，较大的误差出现在再附激波以后的区域，该区域的文献结果与本程序预测结果均低于试验值，但是本程序预测结果更接近于试验值，但最大误差仍然超过了25%，热流密度预测的精度对现有程序来说仍然是一个严峻的挑战.

图4 壁面压力分布Fig.4 Distribution of the wall pressure

图5 壁面热流分布Fig.5 Distribution of the wall heat flux

2.2 高超声速缝隙流动与换热

以Allan 的缝隙流动与换热试验[17]为计算方案，验证程序对高超声速缝隙流动与换热的预测能力.缝隙几何参数如图6 所示，缝隙的宽深比为0.383.来流参数为：Mach 数6.94，Reynolds 数7.45 × 106，压强3 527 Pa，温度154.6 K，攻角0°；出口设置为超音速出口，壁温设置为300 K.

图6 缝隙几何参数（单位：mm）Fig.6 The gap geometry （unit:mm）

研究表明[18]，计算网格对热流密度预测精度影响极大，第一层网格单元的网格Reynolds 数Rec保持在8 左右时可以保证计算的收敛性以及热流的准确性，Rec=Re∞× Δn，其中Re∞与Δn分别表示来流Mach 数与壁面第一层网格至壁面距离；在计算中，采用如图7 所示的拓扑结构进行网格划分，壁面网格第一层单元距离壁面距离保持1.0 × 10-6m，网格增长率设置为1.1，最终网格单元数目为142 256 个.

图7 缝隙流动网格拓扑结构示意图Fig.7 The mesh topology for the hypersonic gap flow

如图8 所示，缝隙入口段上方区域存在一个漩涡，在该漩涡的诱导作用下，缝隙下方区域又形成两个强度较弱的漩涡，该分布符合试验测量的结果.图9 为缝隙中心线上流向速度沿缝深变化的曲线，横坐标x表示距离缝隙入口的距离，即缝隙局部深度，该距离采用缝深参数d做无量纲化，纵坐标表示流向速度.从图中可以看出：与缝隙内漩涡分布相对应，流动速度存在波动，在顶部区域速度波动较大，从170 m/s 迅速降至-60 m/s，但是在x/d约0.5 左右，流动速度的波动已经很小，不超过10 m/s 量级，随着深度的增加，速度波动趋向于0，对流换热对该区域的影响已经很小，传热以导热方式为主.

图8 缝隙内流线Fig.8 Streamlines in the gap

图10 对比了计算得到的缝隙后壁面热流分布，横坐标定义与图9 相同，纵坐标表示壁面热流，采用该位置无缝隙时平板的热流qref做无量纲化.从图中可以看出，由于缝隙顶部存在强剪切流动，对流换热效应显著，局部热流密度较大，随着缝深的增加，对流换热效用逐渐减弱，局部热流密度迅速降低；预测的壁面热流与试验测量值的最大误差约为14%.

图9 缝隙中线流向速度沿缝深变化Fig.9 The velocity distribution along the gap central line

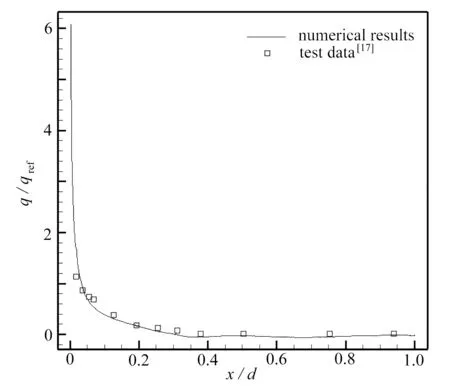
图10 缝隙后壁面热流分布Fig.10 The heat flux on the rear surface of the gap

2.3 无限长圆管高超声速绕流非定常流动与传热

采用与Dechaumphai 等[19]、李佳伟等[20]的研究中相同的计算算例，来流参数为[21]：Mach 数6.47，压强648.1 Pa，温度241.5 K，Reynolds 数1.22 × 105，攻角0°，圆管导热系数与密度参数按照不锈钢材料进行选取.圆管的内外半径分别为25.4 mm 和38.1 mm.采用结构化网格离散计算域，流体区域壁面第一层网格离开壁面距离设置为1.0 × 10-5m，网格增长率设置为1.1；固体区域沿着径向均匀分布；最终流体与固体部分网格单元数目分别为64 × 168，32 × 168；计算网格如图11 所示.

图11 无限长圆管高超声速绕流计算网格Fig.11 Computational grids for the unsteady coupled heat transfer simulation of hypersonic flow over infinite-length pipe

首先对流体域进行定常计算，计算中设置固体温度恒定为294.4 K，收敛后流场参数以及恒定固体温度294.4 K 作为非定常气热耦合计算的初始条件.模拟飞行时间为2 s，由于时间较短，圆管内壁面与气体对流引起的热量交换还比较弱，故在计算中将内壁面设置为绝热壁面.文献[20]的非定常耦合计算对本算例统一采用1.0 ×10-3s 的物理时间步长隐式推进，由于本文在固体域采用显式推进，考虑到推进的稳定性，流场与固体温度场统一采用1.0 × 10-5s 的物理时间步长推进求解.

图12 为非定常气热耦合计算得到的对称线上不同时刻的温度分布曲线.程序预测的激波厚度约为2 mm，在激波内，流体温度从来流值241.5 K 迅速增加到2 100 K 量级，并对固体进行加热.从曲线图来看，温度边界层厚度约为1 mm；在边界层以外区域，不同时刻预测的温度分布差异很小，在边界层内，温度梯度很大，固体表面（对应驻点区域）温度从初始温度294.4 K 增加至390.8 K，而试验测得的2 s 时刻驻点处温度为388.72 K，误差不超过0.53%，说明得到的固体温度结果是可信的.

图12 对称线上温度分布Fig.12 The temperature distribution along the centerline of the cylinder

图13、图14 给出了在t=0 s 时刻流体壁面热流密度与压力分布曲线（均采用驻点处参数做归一化处理），可以看出所开发的计算程序得到的计算结果与试验值吻合程度较好，所得到的流场结果与热流结果是可信的；同时计算得到的t=0 s 时刻的驻点热流密度为68.4 W/cm2，试验值为69 W/cm2，误差不超过1%.

图13 t=0 s 时刻，流固交界面压力分布Fig.13 The pressure on the fluid-solid interface at t=0 s

图14 t=0 s 时刻，流固交界面热流密度分布Fig.14 The heat flux density on the fluid-solid interface at t=0 s

3 结论

笔者基于有限差分法开发了高超声速流动与换热气热耦合求解器，运用该求解器分别对三个典型的高超声速流动与换热算例进行数值仿真，并将计算结果与试验值进行了对比，得到如下结论：

1）以负攻角流过后台阶，在台阶拐点处形成膨胀波，台阶下游附近存在漩涡流动，气体压强、温度等参数降低，热流密度强度减弱，流动再附后形成再附激波，局部压强、温度提高，热流密度骤升.

2）高超声速气流流过缝隙后，在缝隙入口处存在强烈的剪切运动，在顶部漩涡诱导作用下，缝隙底部也存在漩涡流动，但随着缝深的增加，局部流动速度减小，对流换热效应减弱.

3）高超声速气流在钝体前方形成脱体激波，激波后气体温度迅速增加；流场内边界层外气动参数随时间变化差异很小，温度边界层内存在较大的温度梯度，壁面温度随时间持续升高.

4）三个算例仿真得到的气动参数、壁面热流密度的分布与试验测量结果吻合得较好，本文开发的仿真求解器计算能力得到一定的验证；由于激波与附面层的相互干扰，后台阶流动再附激波下游区域得到的热流密度偏离实验较大，热流密度的预测精度有待提高.

致谢本文作者衷心感谢“特种环境复合材料技术国家级重点实验室”基金（JCKYS2019603C003）对本文的资助.