越江地铁盾构隧道管片结构应力混沌时间序列预测模型研究*

范 斌，张 栲，郭 谱

(1.武汉地铁集团有限公司，湖北 武汉 430070； 2.华中科技大学国家数字建造技术创新中心，湖北 武汉 430074；3.华中科技大学土木工程与水利学院，湖北 武汉 430074)

0 引言

由于盾构施工环境具有复杂性，盾构在始发、穿越风井，接收、联络通道等重要区段的施工会造成管片受力的变化，进而引起管片变形，严重时会出现裂缝，导致隧道内涌水涌砂现象发生，造成灾难性的后果。近年来，各地地铁工程安全事故频发，造成了重大的人员、经济损失[1]。GB 50446—2017《盾构法隧道施工及验收规范》中规定了管片结构应力及变形为满足隧道设计与施工的特殊要求进行的选测项目，表明了对管片结构应力的重视。在施工期对管片结构应力进行长期监测和预警，可有效监控隧道结构安全性，具有重要的工程应用价值[2]。目前，随着科学技术的发展，结构应力监测技术也在不断更新，这在一定程度上保障了施工安全，但在风险应对措施还未完善的情况下，如何争取更多的风险反应时间成为亟待解决的问题。因此，管片结构应力预测模型的介入具有重要意义。

现阶段, 进行应力预测、分析的方法主要有回归模型、混合模型、确定性模型、基于最小二乘支持向量机模型、神经网络模型、灰色理论模型等[3-5]。上述方法在一定程度上解决了应力预测问题, 但仍有不足。神经网络模型及灰色理论模型一般只关注数据随时间变化的趋势, 不考虑其他参量(如环境量)的影响。回归、确定性、混合模型等根据原始数据构建一个非时变参数模型，用来描述一个随时间变化的系统，因此，预测误差会随着预测时间的增长而显著增加。目前工程中，上述应力预测的方法大多应用于大坝、桥梁和岩土工程的应力预测，罕见用于管片应力中。以上预测方法大多必须先建立一个主观的系统模型，再利用模型对应力进行预测分析。这需要对研究对象有准确认识，但难以满足，且在选用模型逼近原系统时增加了人为主观性，影响结果的准确性。

针对上述应力预测方法的缺陷，本文提出利用混沌时间序列分析方法。对比上述预测模型，此方法最大优点为直接根据时间序列自身客观规律进行预测，可减少人的主观性对模型建立的影响，进而提高模型准确度[6]。

1 基于神经网络的混沌时间序列预测法

基于神经网络的混沌时间序列预测，即根据混沌理论，计算得到嵌入维数m及延迟时间τ，采用延迟坐标法重构相空间，嵌入维数m即为神经网络输入层节点数，Yn为输入数据，Cn为输出数据，再利用BP神经网络对数据进行神经网络建模，得到预测值。步骤如下。

1)步骤1 相空间重构。利用C-C法计算混沌时间序列的嵌入维数m和延迟时间τ，将原始数据按坐标重构法进行重构，得到输入数据Yn和输出数据Cn。

2)步骤2 初始化网络结构。BP神经网络输入层节点数选为嵌入维数m，输出层节点数为1，动态确定隐含层节点数和激励函数组合。对输入数据Yn和输出数据Cn进行归一化处理。

3)步骤3 网络学习。将经过归一化处理的输入、输出数据导入到神经网络中，采用步骤2所确定的网络参数，进行网络学习，通过BP神经网络中数据的双向传导，实现网络的不断优化，直至最后所得误差下降到能接受的范围。

4)步骤4 进行预测。经过学习后的BP神经网络具有较强的预测能力，将后一组相点输入神经网络中，输出值则为预测值。

2 管片结构应力监测数据初步分析

2.1 工程概况

武汉地铁4号线二期工程越江隧道，地处武汉长江一桥和白沙洲大桥之间，肩负着连接长江两岸的重要使命。隧道始于拦江路站、终至复兴路站，全长约4 000m，区间起点里程为右DK12+687.236，终点里程为右DK15+890.126，开挖基坑深度为54.1m，采用明挖逆作法进行风井内衬墙施工。该隧道区间地理位置如图1所示。

图1 武汉越江地铁盾构隧道区间地理位置

两岸为长江一级阶地，高程20.000～27.000m，南高北低。地势平坦开阔，相对高差一般小于1～3m。地铁隧洞汉阳岸长江一级阶地地层岩性自上而下为：①1层杂填土、①2层素填土，厚3.1～7.3m，成分复杂，结构疏密不均，工程性能相差悬殊；③1层可塑黏土、③2层软～可塑粉质黏土、③5层软～可塑粉质黏土与粉土、粉砂互层，总厚5.0～12.4m，透水性微弱，承载力较低，压缩性中等～高，易产生塑性变形；④2，④3层中密～密实砂类土，总厚1.7～25.6m，压缩性低，承载力一般，透水性中等；⑤层中密～密实圆砾土，压缩性低，承载力高，透水性弱～中等；⑦3层可塑～硬塑状粉质黏土层,压缩性低，承载力一般，基岩为泥岩，强风化带较厚，基本不透水，承载力较高。洞身主要从④2层穿过。

隧道在江底高承压水及软弱地层中掘进，盾构始发接收、穿越风井及联络通道施工均存在很大风险，由于盾构施工环境的复杂性，在始发、穿越风井，接收、联络通道等重要区段的施工会造成管片受力的变化，进而引起管片变形，严重时会出现裂缝，导致隧道内涌水涌砂现象发生，造成灾难性的后果。故应重点监测施工中隧道盾构掘进施工管片承压状态，以降低施工风险，保障人员安全。

2.2 管片结构应力监测

采用振弦式传感器作为管片结构应力传感装置，运用华中科技大学与东北大学合作开发的数据采集仪、现场显示界面、传输设备、地面数据库实现数据的采集、传输和储存。

此数据采集装置具有采集频率高的特点，每个传感器每5min即可采集1组应力或应变数据，每个月约有8 600组海量数据，满足了管片结构应力实时监测的要求，且该海量数据的获取，为之后有关管片结构方面的研究提供了可靠丰富的数据支持。左隧道部分钢筋应力计收集的2013-08应力数据，由于过于庞大，以每2h选取1组数据的标准来构建时间序列，部分时间序列如图2，3所示。

图2 钢筋应力计1232034时间序列

图3 混凝土应变计S/N121613时间序列

2.3 数据初步分析

由图2，3可知，管片结构应力表现出动态、非线性的特征。这是因为管片结构应力受多重因素的影响：在盾构掘进过程中，由于土层未完全达到稳定状态，土体的不规则移动会引起管片应力变化；盾构在江底高承压水中掘进，水压变化也会引起管片应力的改变；除此之外，管片运输车的运行状态及车内运载物体重量变化、盾构机掘进造成的振动、隧道内人员流动甚至隧道内温度的改变均会在一定程度上影响管片结构应力。土体移动、水压变化、盾构掘进造成的振动、管片运输车运行状态、隧道内人员流动等均具有不规则的特征，因此，管片结构应力相应呈现出不规则的变化。根据混沌理论，一个确定性的系统中出现貌似不规则、随机的现象即为混沌行为，从定性角度来看，管片结构应力变化属于混沌行为。

3 混沌时间序列预测模型及管片结构应力预测

3.1 混沌时间序列预测模型

基于混沌时间序列预测方法，确定了混沌时间序列预测模型，模型拓扑结构如图4所示。利用C-C法计算混沌时间序列嵌入维数m和延迟时间τ，将原始数据按坐标重构法进行重构，得到神经网络输入数据Yn和输出数据Cn，输入层节点数则选为嵌入维数m，再对网络进行训练和优化，最终实现管片结构应力预测。

图4 混沌时间序列预测模型

3.2 混沌时间序列预测模型相关参数

随机选取1个含2 000组数据的时间序列段(取最后100组作为预测样本)，从定量角度说明管片结构应力数据的混沌特性，并基于混沌时间序列预测模型对数据进行预测。

采用上述时间序列，分别在不同区间取500个点进行计算，基于MATLAB软件实现C-C法求解混沌时间序列的嵌入维数m及延迟时间τ。不同样本区间所得出的参量变化用统计量曲线表示。根据C-C法，通过统计量曲线变化特征，得到如表1所示的结果。

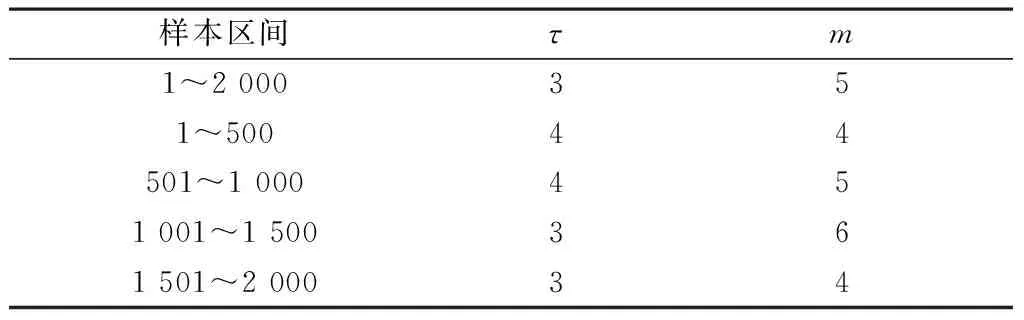
表1 嵌入维数及延迟时间数值

由表1可知，嵌入维数m的值域集中在5左右，而延迟时间τ值域集中在3左右，因此，利用C-C法求得的嵌入维数及延迟时间的结果值得肯定，取m=5和τ=3。

根据已求得的嵌入维数及延迟时间进行相空间重构。为验证时间序列的混沌性可采用Wolf 法计算时间序列的最大Lyapunov指数。利用MATLAB软件进行的Wolf法运算，得到Lyapunov指数分布，若嵌入维数选择正确则曲线会有光滑的部分(或相当水平)。若无光滑部分，尝试其他嵌入维数，观测图中曲线，发现存在光滑部分，进一步说明选取的嵌入维数合理。最终求得最大Lyapunov指数λ=0.648 7>0，即表明该系统具有混沌性。

3.3 BP神经网络参数设定

在保证网络结构、权值及阈值相同的情况下，不同BP神经网络激励函数组合对应的均方误差如表2所示，可知在管片结构应力时间序列预测过程中，激励函数组合的选取会在一定程度上影响BP神经网络预测精度，但影响效果并不大。为达到最优效果，隐含层激励函数选择purelin，输出层激励函数选择tansig。

表2 不同激励函数组合对应均方误差

隐含层节点数直接影响BP神经网络网络性能，包括其输出精度、学习速率、泛华能力等，在实际操作过程中，在MATLAB程序中保持其余变量不变，改变隐含层节点数，得到均方误差随节点数变化的曲线图，曲线图中最小点对应的就是最优的隐含层节点数。不同隐含层节点数 BP 神经网络预测均方误差如表3、图5所示，可知当隐含层节点数为10时，BP神经网络预测精确度达到最高。

表3 不同隐含层节点数对应预测均方误差

图5 不同隐含层节点数对应预测均方误差

BP神经网络拓扑结构如图6所示，属性参数设定如表4，5所示。

图6 BP神经网络拓扑结构

表4 BP神经网络拓扑结构相关参数设定

3.4 管片结构应力时间序列预测结果分析

利用基于BP神经网络的混沌时间序列分析方法对选定管片结构应力时间序列进行预测分析，期望数据、预测数据及两者误差情况输出结果如图7～9所示，再利用MSE(均方误差)，MPE(平均误差百分比)，最大、最小绝对误差，最大、最小误差百分比来衡量预测结果准确度，如表6所示。由表6可知，均方误差为0.031 3<0.05(均方误差越小拟合精确度越高)，平均误差百分比为0.042%<0.1%(平均误差百分比越小，模型拟合精度越高)，因此模型精度符合要求。

表6 BP神经网络精确性度量参数

图7 BP神经网络应力预测输出与期望输出对比

图8 BP神经网络应力预测绝对误差

图9 BP神经网络应力预测误差百分比

4 结语

本文通过对混沌理论和BP神经网络的研究，在混沌时间序列预测方法的基础上，构建了混沌时间序列预测模型。以武汉地铁4号线二期工程盾构隧道实测数据为基础，利用模型进行管片结构应力预测分析，结论如下。

1)将混沌理论引入管片结构应力的分析，并将基于BP神经网络的混沌时间序列预测模型应用于管片结构应力的预测。通过该模型的应用，阐述了管片结构应力混沌性，实现对盾构管片结构应力的预测，并获得较好的精度。

2)数据采用工程实测数据，相较仿真数据的分析，本文结论更为准确、可靠。

3)由于嵌入维数及延迟时间采用C-C法进行计算，有其理论上的劣势，C-C法对于无噪声的数据才能达到最好效果，且本文仅对管片结构应力的1组数据进行了基于混沌时间序列预测模型的预测处理，后续还需对多组数据进行研究。