基于交通状态的离场航班动态协同排序方法
2022-11-09江灏刘继新董欣放
江灏 刘继新 董欣放
(1. 南京航空航天大学 民航学院, 南京 211106; 2. 国家空管飞行流量管理技术重点实验室, 南京 211106)
空中交通需求的持续增长与可用空域和机场资源的长期受限,给空中交通管理带来了新的机遇与挑战。 目前,民航部门投入了大量的人力与物力在繁忙机场新建跑道、更新管制运行设备。但单纯依靠该方法来提高机场和终端区运行容量会受到多种因素(如时间、资金)的制约,已不能作为当前提高交通流量的有效措施。 因此,如何有效地优化和调度时空资源,最大化地发挥现有机场基础设施的潜能,成为空中交通管理领域的研究热点,而在跑道系统中对航班进行进离场排序优化是该领域的典型问题。
离场航班排序和进场航班排序在性质上相似,其区别于进场航班排序之处在于目标函数、间隔要求及求解算法方面[1]。 在目标函数方面,由于离场航班起飞前的整个离场运行过程发生在机场范围内,相较于进场航班排序,需要更多考虑机场方的诉求。 在间隔要求方面,最为不同的是离场航班会受到航路放行间隔的约束,这使得对于进场航班排序问题很容易满足的三角不等式(对于航班序列中的任意3 个航班l、m和k,以Slm、Smk和Slk分别代表航班对lm、mk和lk之间须满足的间隔要求,则三角不等式可表示为Slm+Smk≥Slk),对离场航班排序问题并不总是能够成立。因为在进场着陆的航班对中,后机仅受到与其相邻前机的尾流间隔、水平间隔和进近-塔台移交的协议间隔[2],而离场航班的航路放行间隔并不仅与其相邻前机相关,还须检查所有先前离场的航班。 求解算法方面,动态规划算法能够求解航班排序问题必须满足的先决条件是:航班对之间的间隔满足三角不等式约束,且若离场排序问题中航班之间的间隔不满足三角不等式,问题的复杂度会大幅增加[3-4]。 因此,被广泛应用于求解进场航班排序问题的动态规划算法,在用于求解离场航班排序问题时必须假定离场航班对之间的间隔满足三角不等式[5-8]。 Gupta[9]、Su[10]和Liu[11]等建立了离场航班排序问题的混合整数线性规划模型;分支定界法[12-13]、元启发式算法[3-4]等也被用于解决离场航班排序问题。
近年来,航空运输业呈现多方协同决策的发展趋势,离场航班本身作为空管、航司和机场等多方单位基于各自利益的决策载体,各方秉持不同的诉求。 空管立足运行安全和降低管制负荷,航司着眼运行效率和公平性,机场注重容量提高和放行正常,离场排序的研究重点也由单目标优化逐步转向多目标优化。 Montoya 等[8]、尹嘉男等[14]、Zhang 和Hu[15]、Zhong 等[16]同时考虑多个目标,对离场航班排序问题进行多目标优化。 上述多目标优化相关研究丰富了离场航班排序问题的内涵,但仍存在2 方面问题亟待解决:①如何充分考虑空管、航司和机场的诉求,在对离场航班排序时兼顾各方利益并满足公平性的要求;②如何根据不同时段机场交通状态的差别调整资源,选择合理的优化目标与排序方案。
本文立足于民航运输业多方协同决策的发展趋势,以拥有单条起飞跑道的机场为对象,重点研究机场拥挤与非拥挤场景下离场航班动态协同排序问题。 研究工作着眼于离场航班排序的动态性、协同性和定制化。 在满足离场航班排序的动态性方面,基于离场航班的计划撤轮档时间(scheduled off-block time, SOBT)和预计撤轮档时间(estimated off-block time, EOBT)数据,设计一种离场航班动态排序方法;协同性是指在对离场航班排序时,充分考虑空管、航司和机场的诉求;通过分析拥挤场景与非拥挤场景下各方诉求的差异,定制化地选择目标函数和约束,建立离场航班排序模型。
1 离场航班动态排序方法
在离场航班的SOBT 前150 min,航空公司或航务代理单位会通过领航计划报提交该航班的EOBT。 本文利用EOBT 数据自身具有的动态特性,设计一种离场航班动态排序方法,以满足离场航班排序的动态性要求。 参考滚动时域控制[17](receding horizon control,RHC)中时间窗参数的设置,确定排序时段时长为15 min。
图1 为离场航班动态排序方法流程,各步骤的详细描述如下。
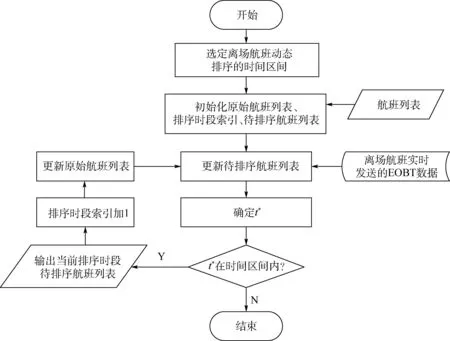
图1 离场航班动态排序方法流程Fig.1 Flowchart of departure flight dynamic sequencing method
步骤1 选定离场航班动态排序的时间区间[Ts,Te],初始化SOBT 在[Ts,Te]之内的原始航班列表L0(按照SOBT 从小到大排序),初始化离场航班排序时段索引i=1,初始化待排序航班列表L1为空。
步骤2 实时接收EOBT 数据,将其所对应的离场航班按照EOBT 由小到大的顺序插入L1相应位置。
步骤3 取L0中第1 个位置离场航班的SOBT 记为t0,取L1中第1 个位置离场航班的EOBT 记为t1,令t*= min{t0,t1}。若t*∈[Ts,Te], 则继续步骤4,否则结束流程。
步骤4t*前150 min 开始计时,计时时长15 min。 计时结束时初始化排序时段i待排序航班列表Li,将L1中EOBT 处于[t*,t*+15]的离场航班加入Li中,并将其从L0和L1中剔除。 触发排序,输出Li作为对当前时段i离场航班排序的初始输入信息。
步骤5 排序时段索引i加1,返回步骤3。
2 模型建立
在协同决策理念下对离场航班排序时,希望同时考虑到空管、航司和机场的诉求,因此针对各方构建了离场航班排序的多个优化目标,并且为保证排序公平性,提出了航空公司延误公平性评价指标。 通过分析机场交通状态拥挤与非拥挤场景下运行特性和各方诉求的差异,确定2 种场景下不同的目标函数和约束,提出一种基于交通状态的离场航班协同排序模型,从而实现各方利益的协同和不同场景下的定制化排序。
本节阐述对第1 节离场航班动态排序方法输出的时段i待排序航班列表Li,进行优化排序的模型建立过程。
2.1 航空公司延误公平性
在一组参与者之间分享有限资源或利益的系统背景下,公平得到了广泛的研究[18]。 航班排序问题中,参与者为各待排序航班,有限资源为跑道时隙资源。 航班次序约束位置交换[19]的应用使得跑道系统在提升运行效率的同时,航班间的相对公平得到保障。 近年来,针对航班排序问题中航班延误公平性的研究已取得了一定的成果[2,15,20]。
而对于单机场航班排序问题而言,空管、航司和机场三方中的航司方也存在多个决策主体,即多个不同航司。 文献[16]通过最小化各航班流方向航班平均延误的差别,实现保证各航班流方向之间延误公平性的目标,借鉴此思路,本文基于各航空公司航班平均延误的差别建立航空公司延误公平性评价指标。
在计算离场航班延误时将离场航班按照是否受到流控影响分为非受控离场航班和受控离场航班。 为实现准点保障的目标,在计算航班延误时将航班提前起飞也当作延误处理。 因此在计算非受控离场航班延误时,其等于优化起飞时间与计

而对于受控航班,全国流量管理系统会以航班计划为基础,依据流量管理措施并按照相关规则发布其计算起飞时间(calculated take off time,CTOT)。 受控航班须在其CTOT 前后一定容差范围内起飞,CTOT 时隙容差分为一类容差和二类容差。 根据《中国民航空管流量管理运行程序》,基于容量管理的流量管理措施为一类容差,容差范围为( -5, +10) min;基于间隔管理的流量管理措施为二类容差,容差范围为( -3, +3) min。为尽可能保障受控航班按照其CTOT 准点起飞,在计算受控离场航班延误时,令其等于优化起飞时间与CTOT 差值的绝对值。

各航司离场航班平均延误的差别越小,航空公司间的延误公平性越高。 因此,在计算航空公司延误公平性评价指标时,对各航司离场航班平均延误的差别进行“取倒数”的处理,从而使各航司离场航班平均延误的差别与航空公司间延误公平性的内涵表征保持一致性。 另外,由于各航司离场航班平均延误的差别存在取值为零的可能,为保证分母的有效性和将航空公司延误公平性评价指标限定在(0,1]范围之内,需以各航司离场航班平均延误的差别取值加上常数1 作为分母。
基于以上分析,本文将航空公司延误公平性评价指标定义为

2.2 目标函数
本文根据空管、航司和机场三方的诉求,建立了三方共同关注的2 个目标函数,并针对各方诉求分别设计了一个目标函数。 其中,最小化离场航班总延误和最大化航空公司延误公平性2 个目标函数同时涉及非受控航班和受控航班。 一般情况下,若某排序时段存在受控航班,该排序时段最后一个离场航班通常为受控航班,其起飞次序较计划起飞次序也会相应地存在较大偏差,并且其优化空间有限,因此对于最小化离场航班次序调整和最大化跑道容量2 个目标,仅考虑非受控航班。 根据《民航航班正常统计办法》中放行正常航班判定标准,受控航班基本不会被判定为放行正常,故对于最大化机场放行正常率目标,亦不将受控航班纳入统计。
1) 综合指标:最小化离场航班总延误
航班延误时间是反映航班延误程度的指标,航班延误对空管社会形象、机场运行效率和航空公司成本效益等均造成了严重影响。 某排序时段离场航班总延误最小,即

2) 综合指标:最小化离场航班次序调整
离场航班优化起飞次序若与计划起飞次序存在偏差,机组会和管制员进行额外的通话,这将增加管制负荷;机场和航司会根据离场航班的离场顺序安排航班保障的先后次序,为保证机场和航司对于离场航班保障服务的平稳、有序和高效运行,优化起飞次序较计划起飞次序的偏离程度应

4) 航司:最大化航空公司延误公平性
由2.1 节可知,航空公司延误公平性评价指标值的大小可直接反映航空公司间的公平性高低。某排序时段内的航空公司延误公平性最高,即

2.3 约束条件
离场航班受到的约束主要有管制间隔要求、时间窗约束和最大约束位置转换(maximum position shift, MPS)约束。
2.3.1 管制间隔要求
空管的安全运行目标通过满足管制间隔要求实现。 离场航班起飞受到的水平间隔约束有非雷达间隔的尾流间隔、跑道运行间隔和放行间隔。
1) 非雷达间隔的尾流间隔

2.3.2 时间窗约束
由于非受控离场航班和受控离场航班时间窗上下界的确定方式存在差异,本文将时间窗约束分为非受控离场航班时间窗约束和受控离场航班时间窗约束。
1) 非受控离场航班时间窗约束
管制运行过程中,管制员会根据不同类型离场航班的重要度,在离场排序时考虑其优先级。在文献[2,16]的基础上,本文将非受控离场航班优先级分为最高等级、次高等级和最低等级3 类,并建立具有各类优先级的非受控离场航班和其可接受的最大延误时间之间的关系。 最高等级的航班重要度最高,常为专机或需要立即起飞离场的航班;次高等级的航班常为国际航班和国内重要航班;最低等级的航班为一般国内普通航班。
因此,非受控离场航班优化起飞时间应当不早于航司提交的该航班EOBT 与其滑行到达离场跑道的最短滑行时间之和,不晚于计划起飞时间

2.3.3 MPS 约束


2.4 基于交通状态的离场航班协同排序模型
根据待排序时段机场交通拥挤程度的不同,选择相应的目标函数和约束对离场航班进行优化排序。 由于本文离场航班排序中的空中交通拥挤识别问题发生于起飞前2 ~3 h,属于短期实时交通管理问题,根据文献[21],宜采用基于短期数据的阈值判别方法。 基于阈值判别的拥挤识别方法,是将交通容量C(即MAP 值)作为阈值,再将交通需求与该阈值进行比较,如果需求大于容量,则判定交通状态为拥挤,否则判定交通状态为非拥挤。
通过以上分析,建立基于交通状态的离场航班协同排序模型如下:

3 算法设计
航班排序问题属于典型的NP-hard[22],而遗传算法作为一种经典的元启发式算法,其并不需要事先描述问题的全部特点及确定算法应采取的措施,特别适合处理此类问题。 因此,采用NSGA-Ⅱ[23]求解2.4 节建立的非线性多目标优化模型。
3.1 算法流程
对第1 节离场航班动态排序方法输出的时段i待排序航班列表Li进行排序计算的算法流程如图2 所示。
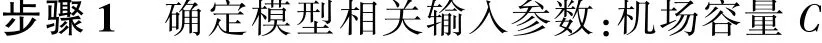
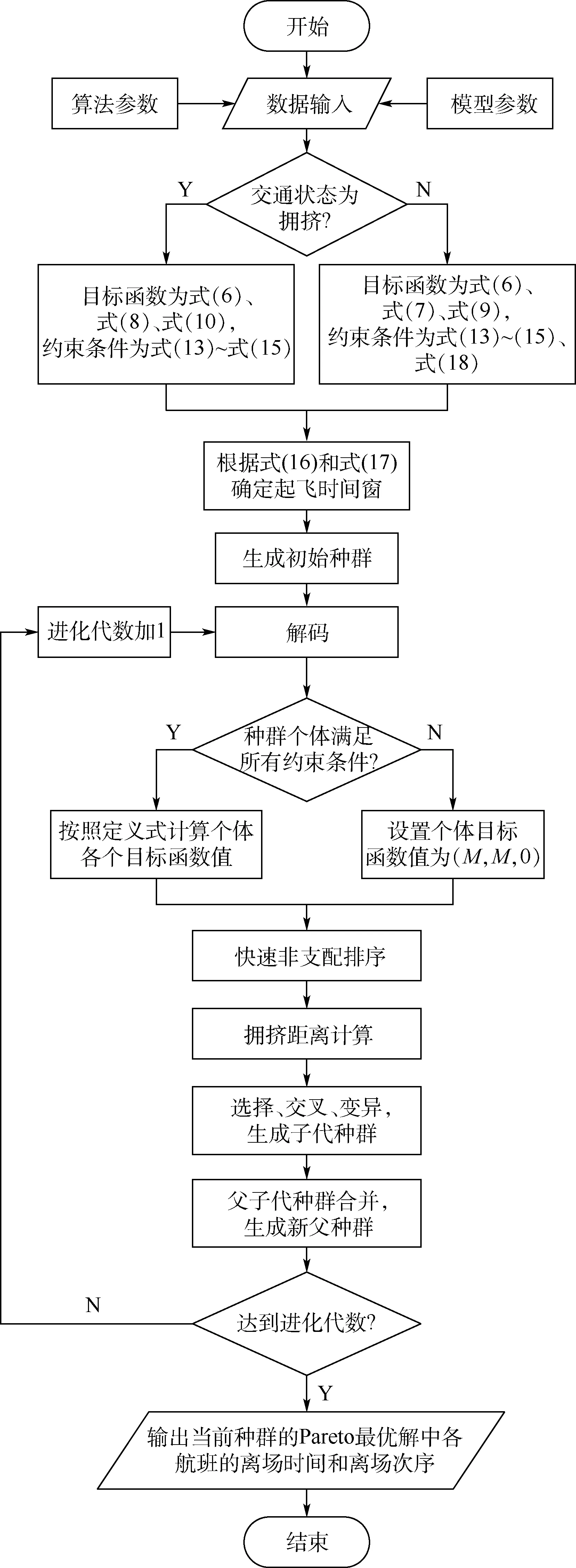
图2 算法流程Fig.2 Flowchart of algorithm

步骤2 根据2.4 节的判别方法判定当前排序时段的交通状态,确定当前排序时段对离场航班排序的目标函数;根据式(16)和式(17)确定所有离场航班的起飞时间窗,以起飞时间窗作为决策变量的上下界,随机生成初始种群。
步骤3 解码,得到各航班的离场时间和离场次序。
步骤4 约束符合性检验。 根据式(13) ~式(15)判断种群各个体初始离场时间是否满足间隔要求(若当前排序时段的交通状态为非拥挤,还须根据式(18)判断初始离场次序是否满足MPS 约束),若满足,根据步骤2 确定的目标函数计算个体的各个目标函数值;若不满足,设置个体的目标函数值为(M,M,0),其中M为一任意大的正数。
步骤5 执行快速非支配排序并计算拥挤距离,基于此进行各种遗传算子操作,得到子代种群;父/子代种群合并,执行快速非支配排序,将处于临界层之前的个体直接保留到下一代,对处于临界层的个体根据拥挤距离从大到小的顺序选择若干个个体保留到下一代,直至新一代种群的个体数目等于父代种群的个体数目。
步骤6 若达到最大进化代数,则当前时段算法运行结束,输出算法运行结果:当前种群的Pareto 最优解中各航班的离场时间和离场次序;若否,进化代数加1,转至步骤3。
3.2 算法实现
1) 非受控航班时间窗约束与MPS 约束处理
考虑到机场和航司双方的诉求,将机场基地航空公司的非受控离场航班优先级设置为次高等级。
2.3.2 节中确定非受控离场航班时间窗约束时,将离场航班优先级与可接受的最大延误时间联系起来。 根据文献[14,16],将最低等级离场航班可接受的最大延误时间设定为40 min;将次高等级离场航班可接受的最大延误时间设定为最低等级的一半,即20 min;由于优先级为最高等级的离场航班重要度很高,参照同样具有高重要度的受控航班,将其可接受的最大延误时间设定为受控航班一类容差的上界10 min;因此,非受控离场航班可接受的最大延误时间集合。
2.3.3 节中确定非受控离场航班MPS 约束时,建立了离场航班优先级与最大位置偏移量之间的联系。 设置非受控航班最大位置偏移量集合为ε={1,2,3}。
2) 编码与解码
在进行模型求解时将以时分形式表示的时间均转换成用秒表示,即将ahbmin 转换成s 的转换公式为:a×3 600 +b×60。 根据2.3.2 节确定的离场航班时间窗,采用整数编码的方式对离场航班的优化起飞时间进行编码。
3) 遗传算子
算法中存在2 个阶段的选择:①采用二元锦标赛选择;②采用基于非支配分层及拥挤距离度量的选择方法,详见文献[23]。 交叉算子为模拟二进制交叉;变异算子为多项式变异。 由于采用整数编码,在使用多项式变异时先按实数值进行突变,再四舍五入进行取整。
3.3 算法性能评价指标
从算法运行过程中各代Pareto 最优解的收敛性和多样性2 个角度出发,选取2 个多目标优化常用的算法性能指标[24]评价多目标离场排序优化解集的优劣。
1) 世代距离
世代距离(generational distance, GD)是用于评价多目标算法收敛性的指标,其值越小说明算法的收敛性越好。 GD 的计算式为
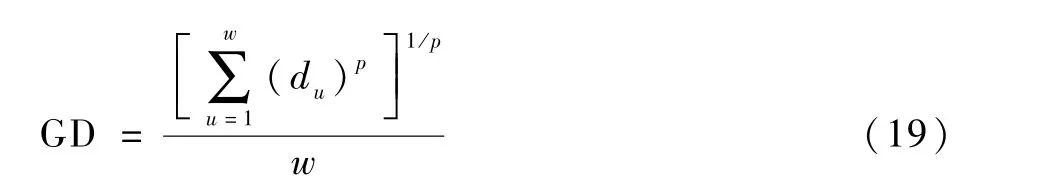
式中:w为算法计算得到的Pareto 前沿中解的个数;p为目标维数;du为算法计算得到的Pareto 前沿中每个解距离真实Pareto 前沿的最近欧氏距离。
2) 反转世代距离
反转世代距离(inverted generational distance,IGD)值不仅能反映多目标算法收敛性,还能反映解的多样性,其值越小则算法的性能越好。 IGD的计算式为

式中:q为真实Pareto 前沿中解的个数;dr为真实Pareto 前沿中每个解距离算法计算得到的Pareto前沿的最近欧氏距离。
4 实例验证
4.1 实验设计
以南京禄口国际机场隔离平行运行模式下的离场运行为例,对离场航班进行动态协同排序。机场的基地航空公司有5 家,分别为:东方航空、深圳航空、吉祥航空、首都航空和邮政航空。 机场的离场点共4 个,分别为:OF、HFE、TESIG 和ESBAG。 研究时段内离场航班机型共2 种,分别为重型机和中型机,无A380-800 型机和轻型机。


3.3 节GD 和IGD 的计算需要以真实Pareto前沿作为参考,而对于实际问题,很难获得真实Pareto 前沿。 通过进行多次独立实验,将各次独立实验获得的Pareto 解集合并为一个集合,在此集合中寻找非支配解,近似替代真实Pareto 前沿。进行独立实验的次数为50 次,独立实验时设置算法的种群规模为200,最大进化代数为300。
4.2 结果分析
将基于先到先服务(FCFS)策略的排序方法(以下简称先到先服务方法)与本文所提的基于交通状态的离场航班动态协同排序方法(以下简称动态协同方法)进行对比,以评估本文方法的优化效果。 选择某典型日7:00—11:00(区间1)和14:00—18:00(区间2)2 个时间区间,共对162 架次(区间1(2):83(79)架次)离场航班进行排序。
在区间1(区间2)内,动态协同方法共包括12 个(12 个)排序时段:拥挤时段3 个(2 个),非拥挤时段9 个(10 个)。 仿真结果表明,拥挤场景和非拥挤场景下各时段算法运行时间均小于5 s,且随着遗传算法进化代数的增加,2 种场景下种群中的个体均朝着最优化方向进化,故其能快速获得最优解。 较先到先服务方法,对区间1(区间2)而言:拥挤场景下,各排序时段平均增加4 种(4 种)排序方案,离场航班总延误平均减少73%(71%);非拥挤场景下,各排序时段平均增加6 种(7 种)排序方案,离场航班总延误平均减少51%(53%),离场航班总次序调整平均减少4 次(5 次),航空公司公平性平均提高3 倍(3 倍)。
以下在拥挤场景和非拥挤场景下各选择1 个时段,对使用先到先服务方法和基于交通状态的离场航班协同排序模型(以下简称优化模型)的排序结果作详细的对比讨论。
1) 拥挤场景
图3 为区间1 第4 个排序时段(11 架次离场航班)的离场航班总延误时间、起飞时间间隔和机场放行正常率在种群进化完成时所得的26 个Pareto 最优解。
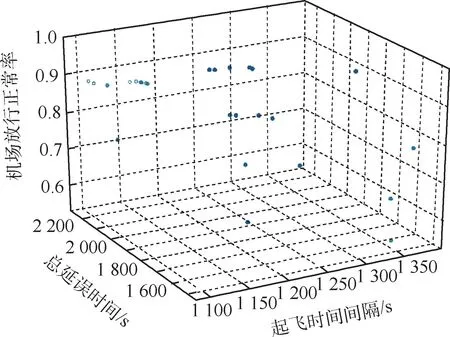
图3 Pareto 最优解(时段1-4)Fig.3 Pareto optimal solution (time interval 1-4)
图4 为区间1 第4 个排序时段在不同进化代数对应的Pareto 最优解集的GD 和IGD 数值变化趋势。 可以看出,随着种群的不断进化,GD 和IGD 数值变化趋势一致,均朝着优化的方向变化,100 代后GD 和IGD 数值趋于稳定。
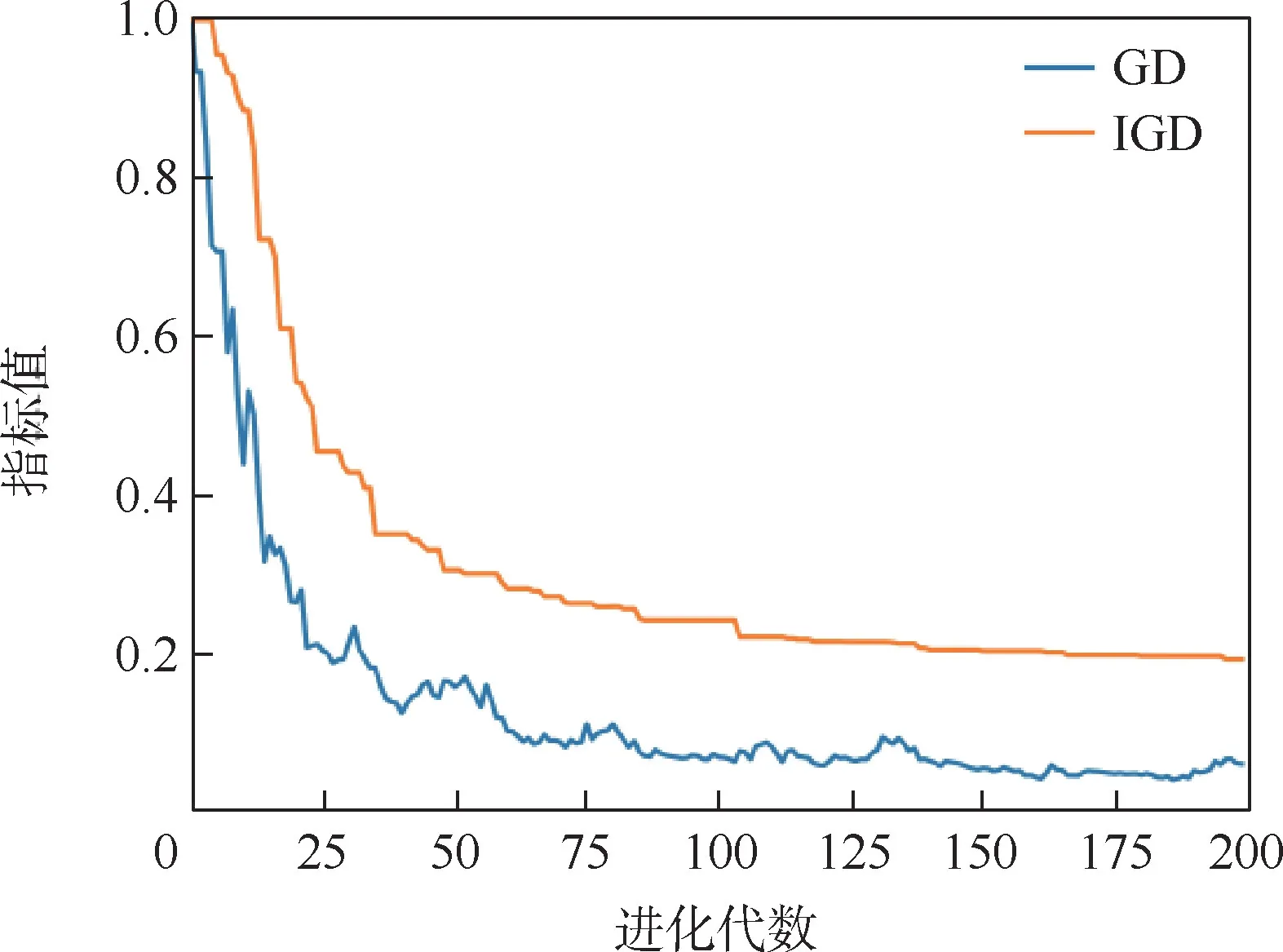
图4 种群进化过程中GD 和IGD 值变化趋势(时段1-4)Fig.4 Trend of GD and IGD value in process of population evolution (time interval 1-4)
拥挤场景下的第3 个目标函数为最大化机场放行正常率,该目标取值为离散值,可能取值的数目等于当前时段待排序离场航班中的非受控航班数加1。 为便于三目标Pareto 最优解的直观展示和对比分析,对拥挤场景下求得的Pareto 最优解按照机场放行正常率取值的不同,绘制各正常率取值下的其他2 个目标函数取值情况图,并将基于先到先服务方法结果的目标函数表现一并展示,如图5 所示。
由图5 所示,基于先到先服务方法的结果不被基于优化模型的Pareto 最优解所支配,同时也不支配基于优化模型的Pareto 最优解。 其在起飞时间间隔与机场放行正常率上的表现较好;但其在离场航班总延误时间上的表现极差:基于优化模型的Pareto 最优解中最大离场航班总延误时间2 222 s,基于先到先服务方法的离场航班总延误时间为8 760 s,约为2 222 s 的4 倍。 因此,基于先到先服务方法的结果因过多的延误难以被接受。
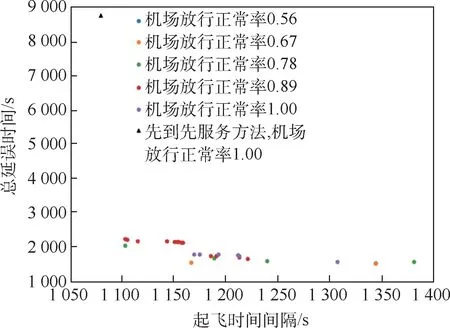
图5 Pareto 最优解与先到先服务方法结果(时段1-4)Fig.5 Pareto optimal and FCFS solution (time interval 1-4)
图6 为区间1 第4 个排序时段基于优化模型的结果与基于先到先服务方法的结果中非受控航班起飞次序情况。 此时段中的2 个受控航班DKH1697 和CRK221 的CTOT 均较晚,且基于优化模型的结果和基于先到先服务方法的结果中这2 个航班均按照CTOT 准点保障,二者的起飞次序位于此时段的最后2 个次序(10 和11)。 由图6可见,基于优化模型的结果提供了4 种离场排序方案,此4 种排序方案与基于先到先服务方法的起飞次序中,CES2893、CES2739 和CSN3578的起飞次序均为7、8 和9。 因此,基于优化模型结果的起飞次序与基于先到先服务方法的起飞次序不同之处主要在于前6 个航班:CES2945、HDA863、CES579、CSZ9571、CES2795 和CBJ5279,其中HDA863 和CBJ5279 的次序差异较大,即优化模型较先到先服务方法的优化主要体现在对此6 个航班起飞次序的优化。
空中交通管理人员可根据Pareto 最优解的性能特点,在离场航班总延误、跑道容量和机场放行正常率之间进行综合权衡。 例如,对区间1 第4个排序时段,希望所选的排序策略航班总延误时间在1 800 s 以下,起飞时间间隔在1 200 s 以下,机场放行正常率在0.8 以上,则从26 个Pareto 最优解中筛选出5 个解,如图7 所示。 此5 个解在各个目标上的差异很小,离场航班总延误最大差异为56 s,起飞时间间隔最大差异为23 s,机场放行正常率最大差异为0.11;此5 个解对应2 种离场排序方案,分别为图6 中的优化模型结果1 和优化模型结果3,注意到此2 种排序方案离场航班次序差异很小,仅为CES2945 与CBJ5279 的次序互换。 经过筛选,Pareto 最优解数目减少至个位数,排序方案减少一半,更有利于管制运行中的选择。
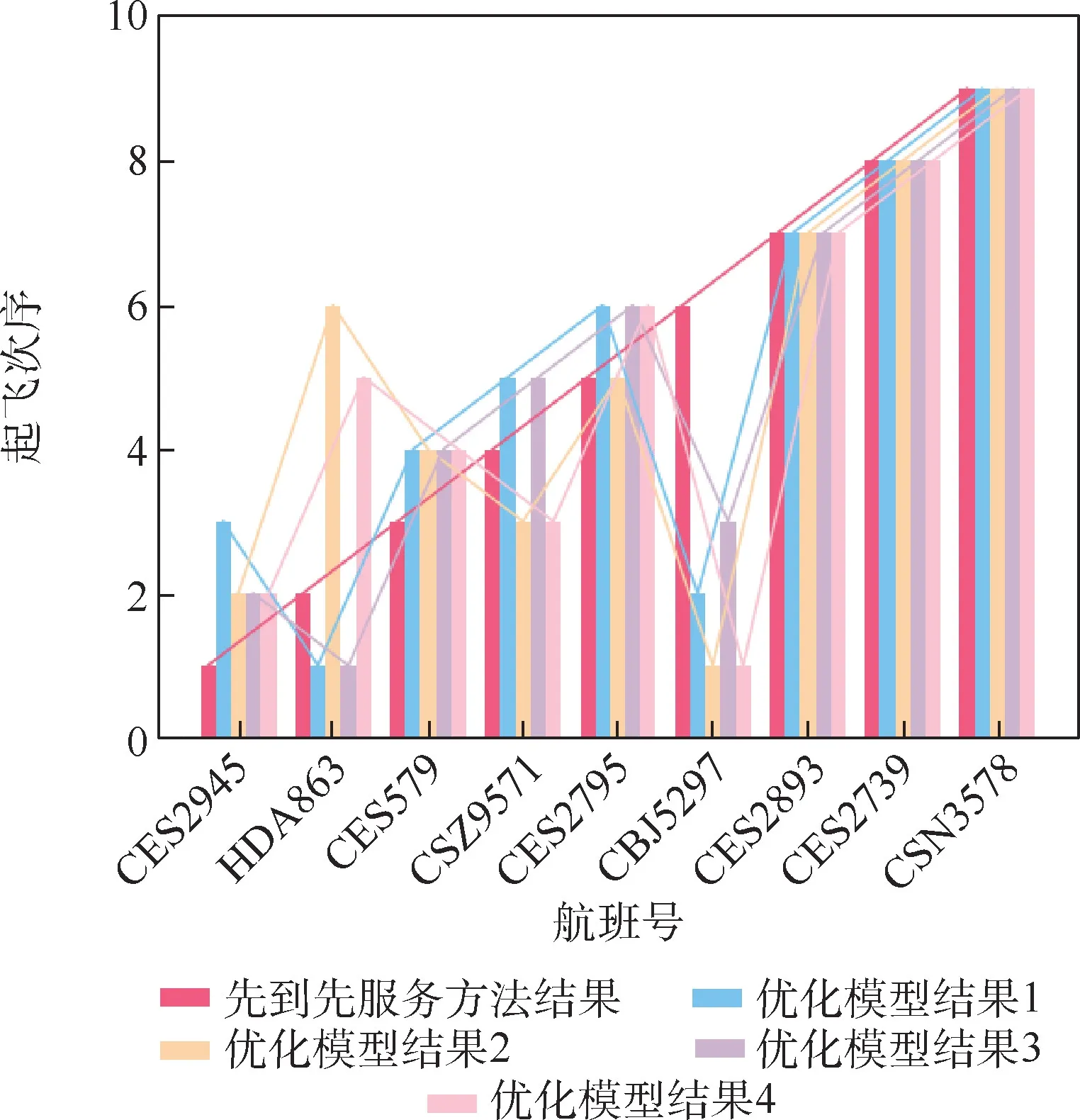
图6 不同策略下离场航班起飞次序(时段1-4)Fig.6 Sequences of departure flights using different strategies (time interval 1-4)
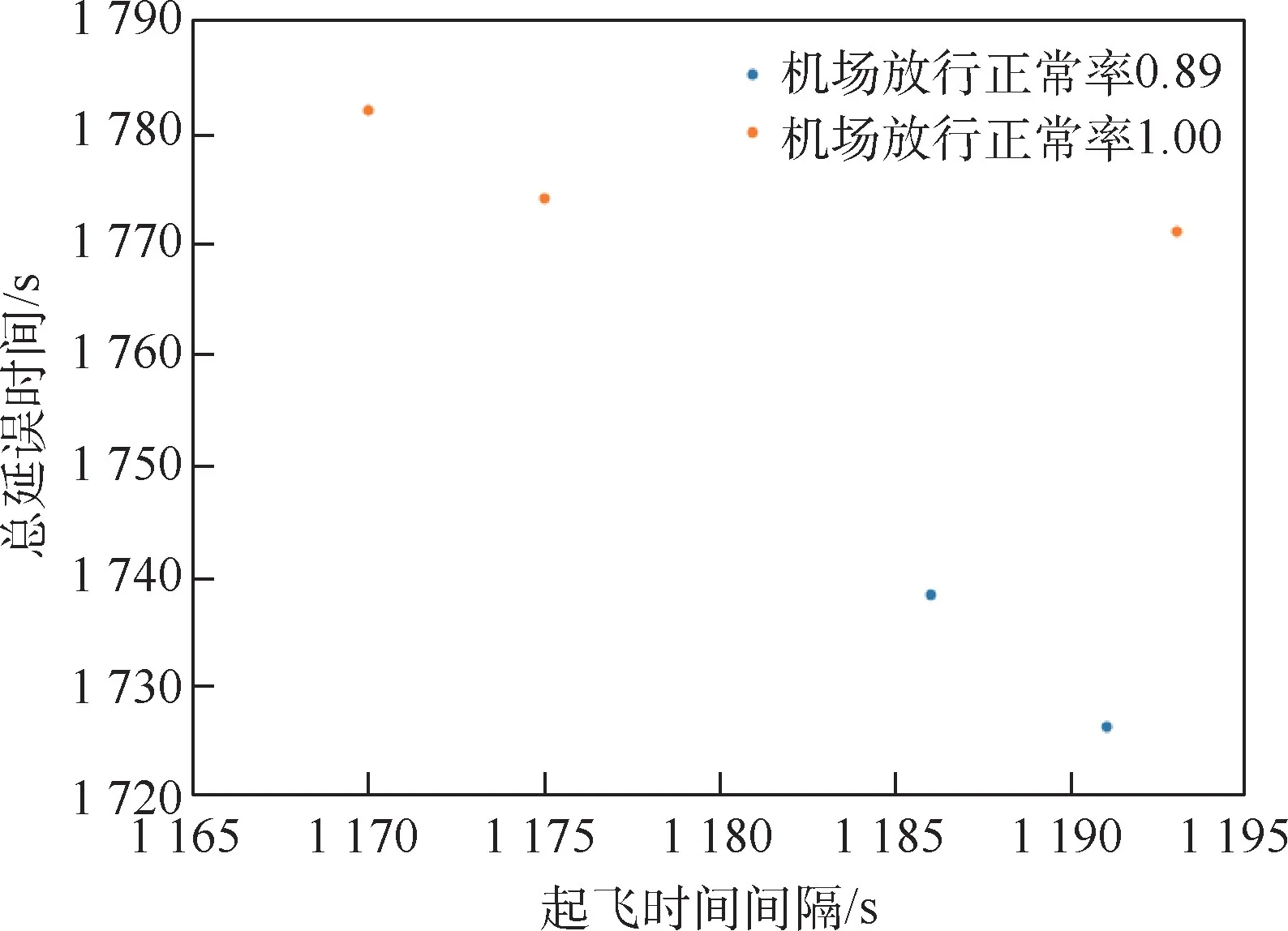
图7 筛选后的Pareto 最优解(时段1-4)Fig.7 Selected Pareto optimal solution (time interval 1-4)
2) 非拥挤场景
图8 为区间2 第2 个排序时段(8 架次离场航班)的离场航班总延误时间、离场航班总次序调整和航空公司延误公平性在种群进化完成时所得的95 个Pareto 最优解。
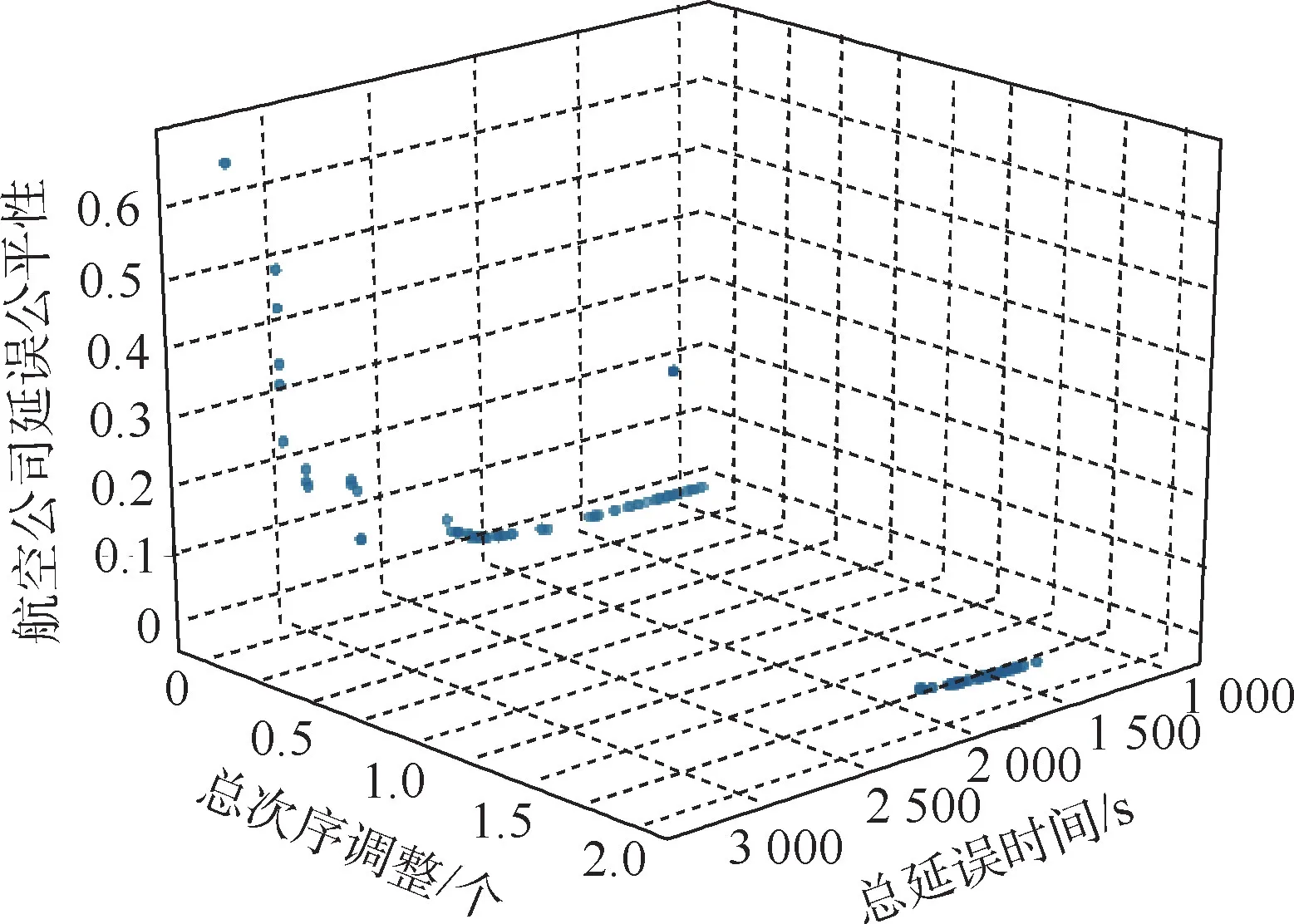
图8 Pareto 最优解(时段2-2)Fig.8 Pareto optimal solution (time interval 1-4)
图9 为区间2 第2 个排序时段在不同进化代数对应的Pareto 最优解集的GD 和IGD 数值变化趋势。 可以看出,随着种群的不断进化,GD 和IGD 数值变化趋势一致,均朝着优化的方向变化,50 代后GD 和IGD 数值趋于稳定。
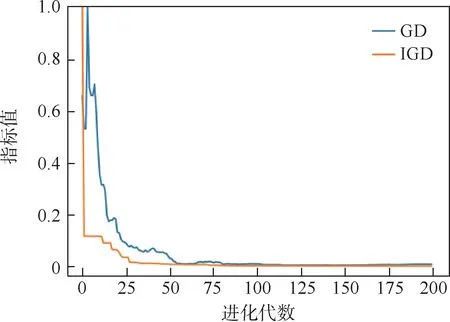
图9 种群进化过程中GD 和IGD 值变化趋势(时段2-2)Fig.9 Trend of GD and IGD value in process of population evolution (time interval 2-2)
与拥挤场景下机场放行正常率取值为离散值相同,非拥挤场景下的第2 个目标函数离场航班总次序调整同样为离散取值。 因此,在非拥挤场景下,仿照拥挤场景对于基于优化模型的Pareto最优解和基于先到先服务方法结果的三目标函数值展现方式,如图10 所示。
由图10 所示,基于先到先服务方法的结果被基于优化模型的Pareto 最优解所支配。 相对于基于优化模型的Pareto 最优解,基于先到先服务方法的结果虽在各个目标上的表现均较差:基于优化模型的Pareto 最优解中最大的离场航班总次序调整最大为2,而基于先到先服务方法结果的离场航班总次序调整为9,为2 的4.5 倍;基于优化模型的Pareto 最优解的离场航班总延误时间最大为3 309 s,而基于先到先服务方法结果的离场航班总延误时间为6 900 s,为3 309 s 的2 倍多;较基于优化模型的Pareto 最优解中最小的航空公司延误公平性0.004 5,基于先到先服务方法结果的航空公司公平性为0.001 2 s,约为0.004 5 s 的1/4。 因此,基于先到先服务方法的结果因过多的次序调整、过多的延误和过低的公平性难以被接受。
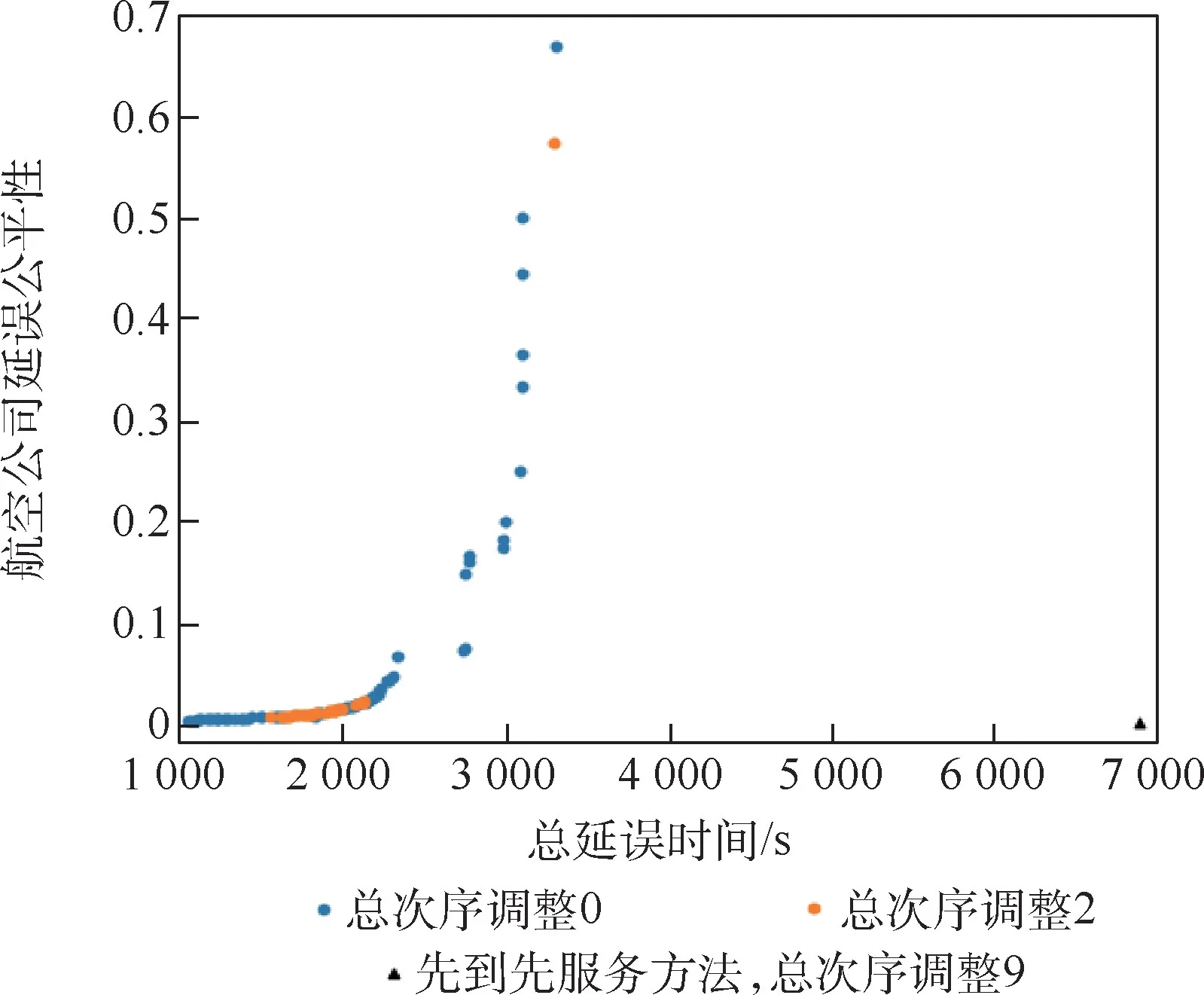
图10 Pareto 最优解与先到先服务方法结果(时段2-2)Fig.10 Pareto optimal and FCFS solution (time interval 2-2)
基于优化模型的Pareto 最优解共提供了7 种离场排序方案,基于先到先到先服务方法结果中非受控航班起飞次序情况、此7 种排序方案中的非受控航班起飞次序及其出现的频次如图11所示。
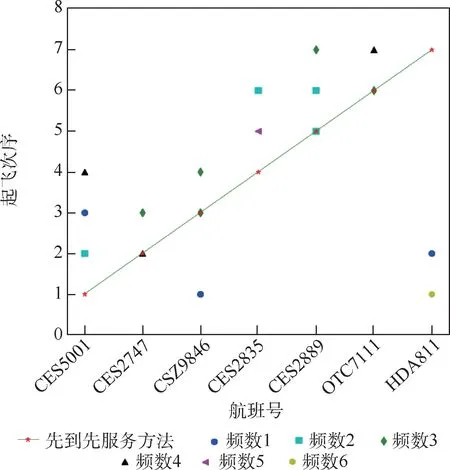
图11 不同策略下离场航班起飞次序频数(时段2-2)Fig.11 Sequence frequency of departure flights using different strategies (time interval 2-2)
此时段中的受控航班CSZ9864 的CTOT 较晚,基于优化模型的结果和基于先到先服务方法的结果中此航班均按照CTOT 准点保障,其起飞次序位于此时段的最后次序(次序8)。 此时段中,HDA811 的计划起飞时间最早,但其预计起飞时间最晚,由图11 所示,基于优化模型结果的HDA811起飞次序均满足MPS 约束,但基于先到先服务方法结果与计划起飞次序偏差过大。 CES5001、CES2747 和CSZ9846 的计划起飞时间相同,因此对于此3 个航班,其计划起飞次序相等,即3 个航班的起飞次序为2、3 和4 中的任一次序,均为按照计划起飞次序起飞。 CES2835 的计划起飞次序为5;同样对于CES2889 和OTC7111 拥有相同的计划起飞时间,二者的计划起飞次序为6 和7。结合以上分析和图11 的结果,基于优化模型的结果各航班最大起飞次序调整量为1,基于先到先服务方法的结果各航班最大起飞次序调整量为6,优化模型在控制离场航班起飞次序偏移方面的效果显著。
空中交通管理人员可根据Pareto 最优解的性能特点,在离场航班总延误时间、离场航班总次序调整和航空公司延误公平性之间进行综合权衡。例如,对区间2 第2 个排序时段,希望所选的排序策略航班总延误时间在2 000 s 以下,航空公司平均延误时间偏差在120 s 以下(即航空公司延误公平性在0.008 3 以上),则从95 个Pareto 最优解中筛选出28 个解,如图12 所示。 此28 个解对应2 种离场排序方案,分别为2-3-4-5-7-6-1 和4-2-3-6-5-7-1,经过筛选,排序方案减少至2 个,更有利于管制运行中的选择。
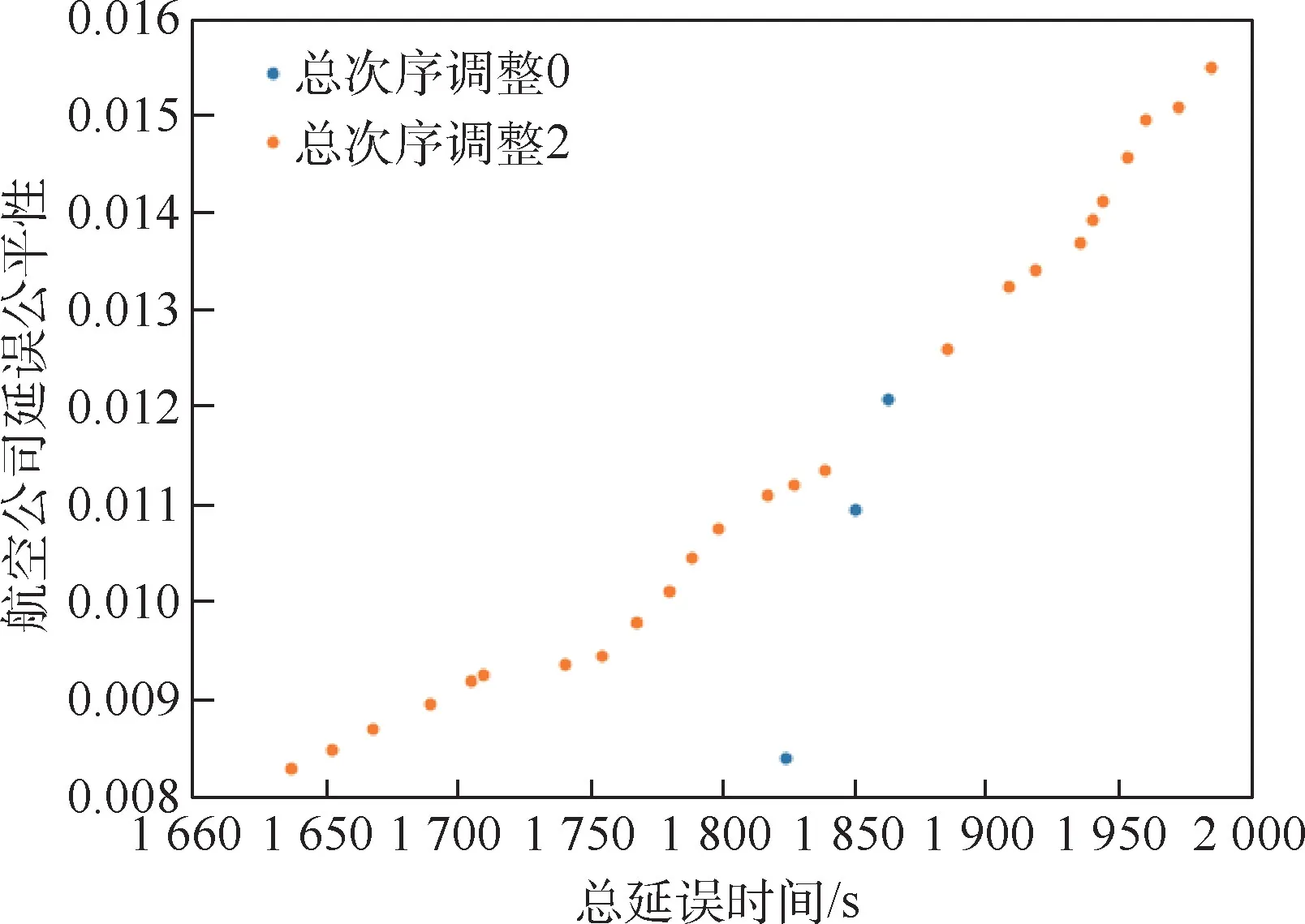
图12 筛选后的Pareto 最优解(时段2-2)Fig.12 Selected Pareto optimal solution (time interval 2-2)
5 结 论
1) 利用离场航班EOBT 数据自身具有的动态特性,结合离场航班SOBT 数据,设计了一种离场航班动态排序方法,将某一时间区间划分为多个排序时段,缩小了问题的求解规模,满足了离场航班排序的动态性要求。
2) 从保障航空公司间的延误公平性考虑,对各航空公司离场航班平均延误的差别进行转化,提出了航空公司延误公平性评价指标,用于航空公司延误公平性的定量计算。
3) 根据不同类型离场航班的重要度,在离场排序时考虑其优先级。 将非受控离场航班优先级分为3 类,建立具有各类优先级的非受控离场航班和其可接受的最大延误时间、MPS 约束中最大位置偏移量之间的关系;考虑机场和航空公司双方的诉求,将机场基地航空公司的非受控离场航班优先级设置为次高等级。
4) 针对机场交通拥挤和非拥挤场景,分析空管、航司和机场在2 种场景下的不同利益需求,确定相应的目标函数及约束,建立了基于交通状态的离场航班协同排序模型,设计了相应的求解算法,所提方法可为空中交通管理人员制定航班排序方案提供理论支撑。
