基于BABFA 的XNOR/OR 电路面积优化
2022-11-09周宇豪何振学梁新艺范新超霍志胜肖利民
周宇豪 何振学 梁新艺 范新超 霍志胜 肖利民
(1. 河北农业大学 河北省农业大数据重点实验室, 保定 071001; 2. 泰安市妇幼保健院 信息管理科, 泰安 271000;3. 北京航空航天大学 高性能计算平台, 北京 100083; 4. 北京航空航天大学 软件学院, 北京 100083;5. 北京航空航天大学 计算机学院, 北京 100083)
逻辑电路展开式越精练,电路实现就越简单,所需要的门电路就越少,电路的面积、功耗也就具有显著优势。 数字逻辑电路既可以由基于AND/OR/NOT 的Boolean 逻辑实现,也可以由基于XNOR/OR 或XOR/AND 的Reed-Muller(RM)逻辑实现。 对部分电路来说,与Boolean 逻辑相比,RM 逻辑实现的电路形式具有更简洁的结构、更小的面积和功耗,以及更好的可靠性。 此外,与基于XOR/AND 的表达式相比,基于XNOR/OR 的部分电路表达式更加简洁。 因此,基于XNOR/OR 的RM 电路的综合优化正引起越来越多研究者的参与。
极性优化是RM 电路综合性能优化的重要技术手段。 任意一个n变量的逻辑函数都具有2n个固定极性,对应2n个繁简程度不同的固定极性RM(FPRM)展开式。 基于XNOR/OR 的FPRM 电路极性优化即是在所属极性空间中搜索一个最优极性,使其电路目标函数值最优。 小规模电路一般采用穷尽搜索策略,通过对电路全部极性的评估和比较获得最佳极性。 中大规模电路的极性优化通常采用智能优化算法,以便在可接受时间范围内获得问题的最优解。
2002 年,细菌觅食算法(bacterial foraging algorithm,BFA)首先由Passino 教授[1]通过模拟人体肠道中大肠杆菌的觅食行为提出。 BFA 实现简单,具有较好的全局寻优性能,一经提出,就受到国内外研究者的广泛关注。 到目前为止,研究者们已经提出了一系列的BFA 的改进方案,这些改进的BFA 有效解决了现实世界中的一系列优化问题。 在对BFA 的改进中,主要涉及复制和迁徙操作,自适应步长机制、群体感应机制,以及与其他启发式算法融合等。 Supriyono 和Tokhi[2]提出了基于各类数学函数的3 个不同的自适应步长BFA 模型。 Majhi 等[3]用BFO 和ABFO 通过最小化均方差对基于模型的自适应线性组合的连接权重进行优化。 Treaty 和Mishap[4]根据各类问题,改进适应度函数,设计出了基于改进适应度函数的BFA。 Amaresh[5]利用BFA 结合数据处理分组法估计了保护农场的最低能耗消耗指数。 Liu等[6]把BFA 改进为一个基于五阶段的启发式算法用在生产计划中。 Cai 等[7]采用了启发式混合BFA 来搜索最优位姿。 Ye 等[8]将粒子群算法引入到改进的BFA 中,处理数据分类问题。 Zhang等[9]提出了一种具有自适应消除和分散概率的BFA,以提高参数的收敛速度。 Liu 等[10]将混合策略引入到BFA 中,避免了冗余的本地搜索。 李珺[11]在BFA 中改变了算法的复制和迁徙规则,在复制操作中,对个体优秀程度的评价可以仅依据细菌个体当前的适应度值来进行,在迁徙操作中,迁徙操作的作用范围不再是整个群体,而是排在后面的适应度值较差的那部分个体。 Hu 等[12]提出了一种改进的多模态BFA。 在现有的研究中,对BFA 的改进大多是针对趋化步长,在游动、复制迁徙操作方面改进较少。
本文提出了一种基于XNOR/OR 的FPRM 电路面积优化方法,利用提出的二进制自适应BFA(BABFA)搜索对应电路面积最小的最佳极性,验证了该方法的有效性。
1 基于XNOR/OR 的FPRM 电路面积优化理论基础
1.1 XNOR/OR 电路表达式
任意n变量的逻辑函数都可以由基于XNOR/OR 的FPRM 展开式表示,即

式中:k∈{0,1,…,n-1};dj∈{0,1},dj=0 表示sj项在表达式中出现,dj=1 表示该项不在表达式中出现。 在固定极性XNOR/OR 展开式中,每个变量只能以原变量或反变量2 种形式中的一种出现,不能同时以原变量和反变量的形式出现。 极性表示变量出现的形式,即极性0 表示变量以原变量形式出现,极性1 表示变量以反变量形式出现。 因此,任意n个变量的逻辑函数都有2n个固定极性,对应2n个复杂度不同的FPRM 展开式。
1.2 电路面积优化数学模型
由式(1)可知, 基于XNOR/OR 的FPRM 电路展开式由多输入XNOR 操作和多输入OR 操作组成,因此,电路面积大小可以用XNOR 和OR两操作的项数之和来表示。 由于逻辑运算的输入输出关系复杂,在面积计算前需要将多输入逻辑运算分解成二输入运算,此时,电路的面积则为二输入XNOR 门及二输入OR 门的和。
由式(1)和式(2)可得,多输入OR 门si分解为mi个二输入OR 操作,则有

例如,1 个四变量固定极性XNOR/OR 表达式为f=☉∏(0,1,3,7,8,12,15),假设4 个输入变量分别为x3、x2、x1、x0,极性的二进制形式为0110,即变量x1和x2在表达式中以反变量的形式来表示,而变量x0和x3在表达式中以原变量的形式表示。 该函数可表示为
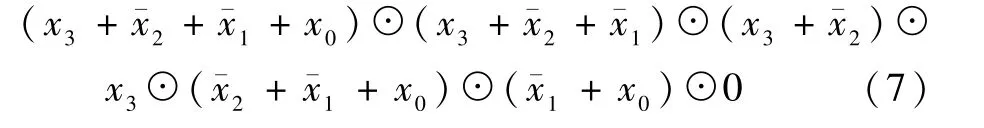
式中:ˉx2表示反变量;“☉”表示XNOR(同或)。
根据上述电路面积数学模型,可得XNOR 项和OR 项的总数为15,即电路面积为15。
2 二进制自适应细菌觅食算法
2.1 细菌觅食算法
BFA 主要通过趋向性操作、复制操作和迁徙操作的迭代计算来搜索问题的最优解。 算法流程如图1所示。
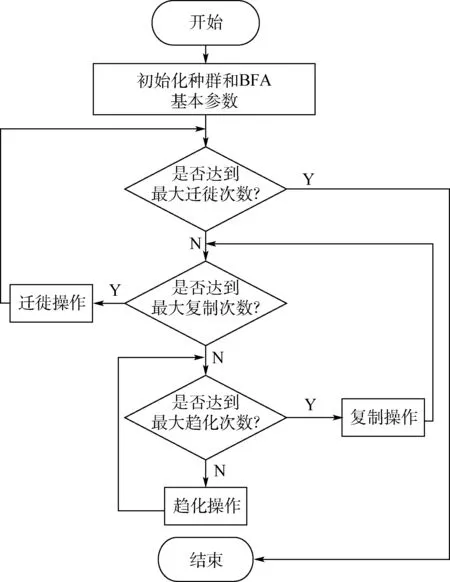
图1 细菌觅食算法流程Fig.1 Flow chart of bacterial foraging algorithm
BFA 主要通过趋化操作更新细菌个体的位置进行寻优,通过复制操作加速算法的收敛速度,并利用迁徙操作防止算法陷入局部最优。 在趋化操作中,其主要步骤为游动和旋转。 在进行趋化操作时,细菌会随机产生一个方向,再进行移动,如果该方向上的适应度更好,则细菌发生游动,否则,细菌继续停留在原地。 此外,从图1 还可以看出,细菌群体每进行一次复制操作,就会进行最大次数的趋化操作,这就等价于种群的不断迭代过程,而细菌的趋化操作就是不停地寻找最优解的过程。 因此,BFA 往往迭代一次就能够快速找到最优解。 当达到最大复制次数时,根据迁移概率进行迁移操作,每进行一次迁移操作,细菌就要再次进行复制操作和趋化操作,直到达到最大迁移次数,跳出循环。
2.2 细菌觅食算法的分析及改进
传统BFA 在整个进化过程中对复制环节采用的是将个体在上一次趋向性操作循环中取得的所有适应度值求和,得到个体当前的健康度。 按照细菌个体的健康度,对整个菌群进行排序,健康度越高的个体,排序后位置越靠前。 根据优胜劣汰法则,将排序后健康度较差的一半细菌个体淘汰,剩余的一半健康度较好的细菌个体进行自我复制,这会大大降低种群的多样性。 因此,结合遗传算法的交叉概率的思想,对复制操作添加一个复制概率Pc,以增加下一代种群的多样性。 同迁移率一起用模糊控制规则来确定。
传统BFA 采取固定的迁徙概率,限制了算法的寻优能力和效率。 但是,怎样在算法进化过程中对迁徙概率Pm采取自适应的变化是一个相对复杂的问题,用数学公式形式化描述相对困难,而基于模糊规则的参数选择法是解决此类问题的一种有效方法。 不同于传统的求解自适应概率,基于模糊规则的二进制自适应采用查询表的方式,在实际应用中,大大缩短了求解传统自适应概率所需参数所浪费的时间,具有更快的收敛速度。
自从Zandeh 在1965 年提出模糊集合的理念后,基于模糊集合理论的模糊控制开始迅速发展,研究者们把模糊控制思想引入到遗传算法、粒子群算法等众多智能优化算法中,如提出模糊遗传算法(FGA)以改善算法的优化效果,并提高算法的收敛速度。 邓莉和鲁瑞华[13]所提的模糊遗传算法中,将具有不确定性概念的交易时间采用模糊集理论来描述。 李擎等[14]将输入变量Pc和Pm做了归一化处理,改进了算法的适用范围,但在迭代过程中,该方法需要对交叉和待变异个体分别计算交叉概率和变异概率,增加了程序的运行时间。 张会红等[15]克服了上述缺陷,简化了归一化处理,但是还需要分别计算清晰化后的交叉概率和变异概率。
本文提出BABFA,Pc和Pm的值能随着迭代的进行而自适应地变化,并采用查询表的方式进行选择。 这种有自组织性能的BFA 将具有更高的鲁棒性、全局最优性和更快的收敛速度。
2.2.1Pc和Pm自适应变化
Pc和Pm的确定频率设定为每代1 次,设Fmax和Fave分别表示当代群体的最大适应度值和平均适应度值,Fng表示最大适应度值未进化代数,即当前的最佳适应度值经历了多少次迭代依旧未找到比当前更优秀的适应度值。 对Pc和Pm确定的基本控制思想如下:
1) 若Fmax-Fave较小,说明算法在当前适应度极值附近迭代趋于成熟,应减小Pc,增大Pm;若Fmax-Fave较大,说明算法处于正常进化趋势,Pc和Pm可取正常值。
2) 若Fng较小,说明算法处于正常进化趋势,Pc和Pm可取正常值;反之,说明算法有局部收敛趋势,应减小Pc,增大Pm。
为此,需要有模糊控制器的输入量,并将两输入量做如下归一化处理:


式中:Fmin为当代群体的最小适应度值。 经过归一化处理后,Fc和Fm的基本论域均变为(0,1)。其模糊量以Ac和Am表示,根据算法进化实际情况,将两输入的语言值均取为3 个:大(B)、中(C)、小(S)。 将两输出的变量对应的模糊量为Pc和Pm,其模糊量以DC 和DM 表示,定义其词集为T(DC) =T(DM) = {VS,S,C,P,VP},本文对DC 和DM 的清晰化的值均为{0.1,0. 3,0.5,0.7,0.9},其中,VS 为非常小,S 为小,C 为中等,P 为大,VP 为非常大。
根据上文所述模糊理论的基本控制思想,对Pc和Pm分别建立了9 条模糊控制规则,具体如表1和表2 所示。
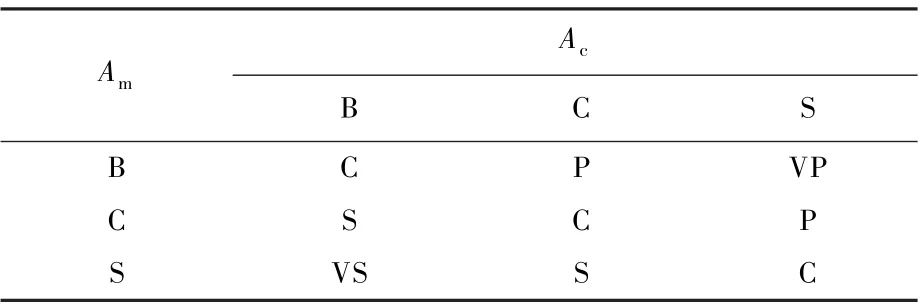
表1 Pc 模糊控制表Table 1 Pc Fuzzy control table
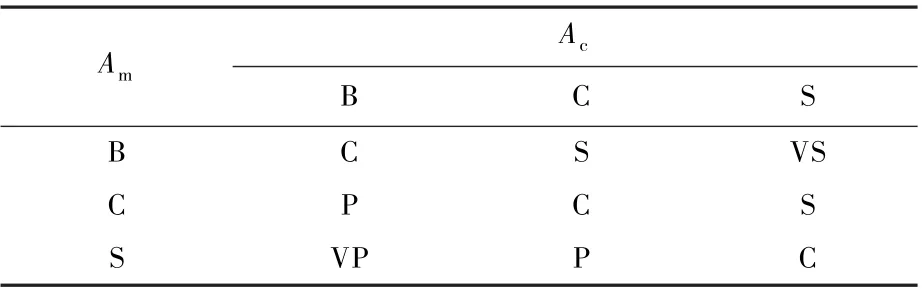
表2 Pm 模糊控制表Table 2 Pm Fuzzy control table
将DC 和DM、Ac和Am清晰化后再利用查询表的方式得到Pc和Pm的值。 本文对Ac和Am清晰化具体值如下:

例如,从式(8)和式(9)得出Fc和Fm分别为0.4 和8。 根据式(10)和式(11),其对应的语言值分别为S 和B,再根据表1 和表2,查询对应的两输出的变量Pc和Pm分别为VP 和VS,设定的VP 和VS 清晰化的值分别为0.9 和0.1,得出复制概率为0.9,迁徙概率为0.1。
2.2.2 趋化操作改进
BFA 模拟了大肠杆菌的觅食操作,大肠杆菌全身长满了鞭毛,它们在觅食过程中通过鞭毛的转动来搜索富含营养物质的区域,并向之翻转和游动,把翻转和游动统称为趋向性操作。 趋向性操作是BFA 的核心操作。 如图2 所示,BABFA在趋向性操作中使细菌在邻域搜索,即使细菌在自己的最大半径范围内搜索,最大半径看作是细菌游动最大次数,其中,箭头表示翻转和前进方向。 无需再计算其他细菌对自己的影响,增强了细菌的局部搜索能力,提高了BFA 的寻优能力。
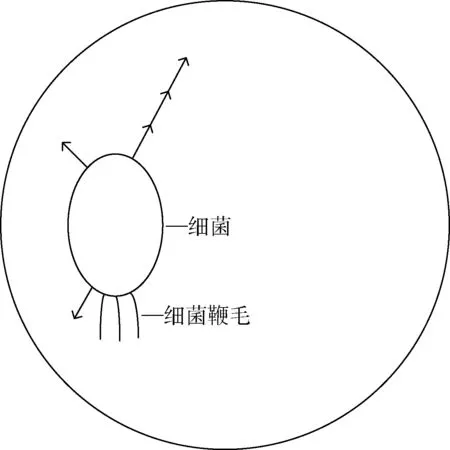
图2 细菌趋化半径Fig.2 Bacterial chemotactic radius
2.2.3 算法描述


输出最优解。
首先,初始化种群和各项参数,Nc为细菌最多翻转的方向次数,Nre为细菌种群最大复制次数,Ned为细菌种群最大迁徙次数。 其次,细菌开始进行趋化操作。 然后,在当前方向进行设定的最大前进次数的搜索,得到每一次搜索的适应度值,同时保存最大适应度值和最小适应度值,直到达到最大翻转方向的次数。 当所有细菌个体进行完翻转操作之后,计算出平均适应度值和最大适应度值未进化代数,为复制操作提供参数,得到种群的复制概率。 最后,选择性地把适应度好的个体复制给适应度差的个体,在进行完复制操作之后,重复之前的趋化操作,直至重复到最大复制次数之后,进行一次迁徙操作,直到满足最大迁徙次数。
3 基于XNOR/OR 的FPRM 电路面积优化
固定极性XNOR/OR 电路面积优化是典型的组合优化问题。 小规模电路面积优化可采取穷举策略实现。 当电路输入变量增大时,采用穷举搜索策略将难以在较短时间内获得问题的满意解。因此,本文提出一种基于XNOR/OR 的FPRM 电路面积优化方法,该方法利用提出的BABFA 来搜索对应电路面积最小的最佳极性,从而实现电路面积优化。 如图3 所示,在BABFA 中,对极性进行二进制编码,算法在进化搜索中基于个体的适应度和电路面积数学模型来进行搜索,其面积优化步骤描述如下:

图3 FPRM 电路面积优化流程Fig.3 Flow chart of FPRM circuits area optimization
步骤1 读入电路,初始化细菌种群规模、趋向性翻转操作次数、游动次数、复制操作次数、迁徙操作次数等进化参数,并根据适应度函数,计算出初始种群的适应度值。
步骤2 细菌开始趋化操作,即进行翻转和前进。
步骤3 细菌进行完最大翻转次数后,得出最大、最小及平均适应度值,以及当前最大适应度值未进化代数,即当前的最佳适应度值经历了多少次迭代依旧未找到比当前值更高的适应度值。
步骤4 得到各类模糊规则所需要的参数,并采用查询表的方式为复制操作和迁徙操作提供概率值。
步骤5 对细菌的适应度值进行评价并按照升序排列。 将前面N/2 个细菌个体的位置按照概率复制给排列在后面的N/2 个细菌个体。
步骤6 复制之后返回步骤2 继续执行趋化操作,直到达到最大复制次数。
步骤7 复制操作达到最大次数后,进行种群的迁徙操作,按照迁徙概率对种群进行迁徙操作,即对细菌个体的长度,随机产生一个迁徙位置,将0 变为1,或者1 变为0。
步骤8 迁徙之后返回步骤2 继续执行趋化操作,即每进行一次复制操作细菌就要再次进行趋化操作,每进行一次迁徙操作细菌就要再次进行复制和趋化操作,直到达到最大迁徙次数。
4 实验结果与分析
本文算法均用C 语言实现,在Windows 10 操作系统下,通过VS 2019 编译,程序的硬件环境为Intel(R)Core(TM)i7-8750 CPU(2. 20 GHZ)8 GB RAM。 测试电路均采用PLA 格式MCNC 基准电路。
为了验证BABFA 的性能及其在固定极性XNOR/OR 电路面积优化上的优越性,实验将BABFA 与传统遗传算法(TGA)、传统细菌觅食算法(TBFA)、文献[11]所提改进的细菌觅食算法(IBFA)进行比较。 4 种算法的迭代次数均设定为100,复制和迁徙次数均设定为10,种群规模设为8。 从MCNC 基准电路测试集中随机选取12 个电路作为实验电路。 由于4 种算法都具有随机性,实验将每个算法在每个测试电路上运行10 次,并将实验结果的最优值和平均值作为实验数据。
4.1 电路面积对比
4 种算法的电路面积优化对比数据如表3 所示。 其中,best 表示10 次运行中求得的电路最小面积;average 表示10 次运行中求得的电路最小面积的平均值;save_best 中的save1 表示BABFA 与TGA 比较所节省的面积百分比,save2 表示BABFA与TBFA 比较所节省的面积百分比,save3 表示BABFA 与IBFA 比较所节省的面积百分比;save_average 中的save1 表示BABFA 与TGA 比较所节省的最小面积平均值百分比,save2 表示BABFA 与TBFA 比较所节省的最小面积平均值百分比,save3表示BABFA 与IBFA 比较所节省的最小面积平均值百分比。
由表3 可知,对于输入变量数较小的电路来说,4 种算法获得的最优解相同,但BABFA 得到的最小面积的平均值要略优于其他3 种算法。 对于输入变量数较大的电路来说,BABFA 得到的最小面积优于其他3 种算法,且平均值明显优于其他3 种算法。 分析可得,BABFA 比TGA 在面积上平均节省了11%;BABFA 比TBFA 在面积上平均节省了18%;BABFA 比IBFA 在面积上平均节省了15%。
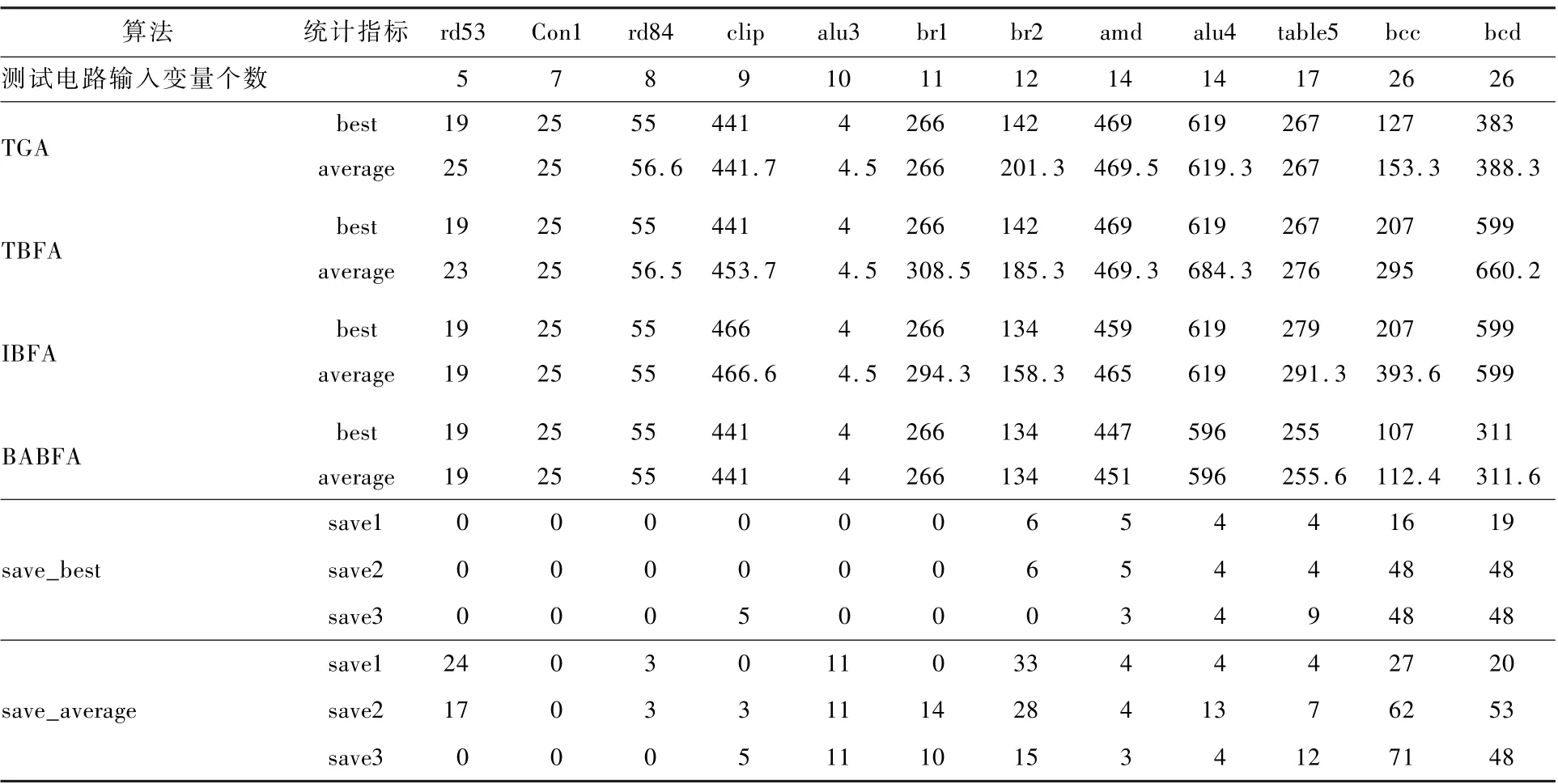
表3 四种算法在面积优化上的实验结果Table 3 Experimental results of four algorithms on area optimization
4.2 优化时间对比
将每个算法在每个测试电路上运行10 次,并将实验结果的平均值作为实验数据。 4 种算法的电路运行时间对比数据如表4 所示。 其中,save1_TGA 表示BABFA 与TGA 比较CPU 运行时间所节省的百分比,save2_TBFA 表示BABFA 与TBFA比较CPU 运行时间所节省的百分比,save3_IBFA表示BABFA 与IBFA 比较CPU 运行时间所节省的百分比。
由表4 可知,在输入变量少的电路中,BABFA节省时间的百分比较小,但在输入变量大的电路中,BABFA 节省时间的百分比非常明显。 分析可得,BABFA 比TGA 在时间上平均节省了46%,BABFA 比TBFA 在时间上平均节省了36%,BABFA 比IBFA 在时间上平均节省了32%。
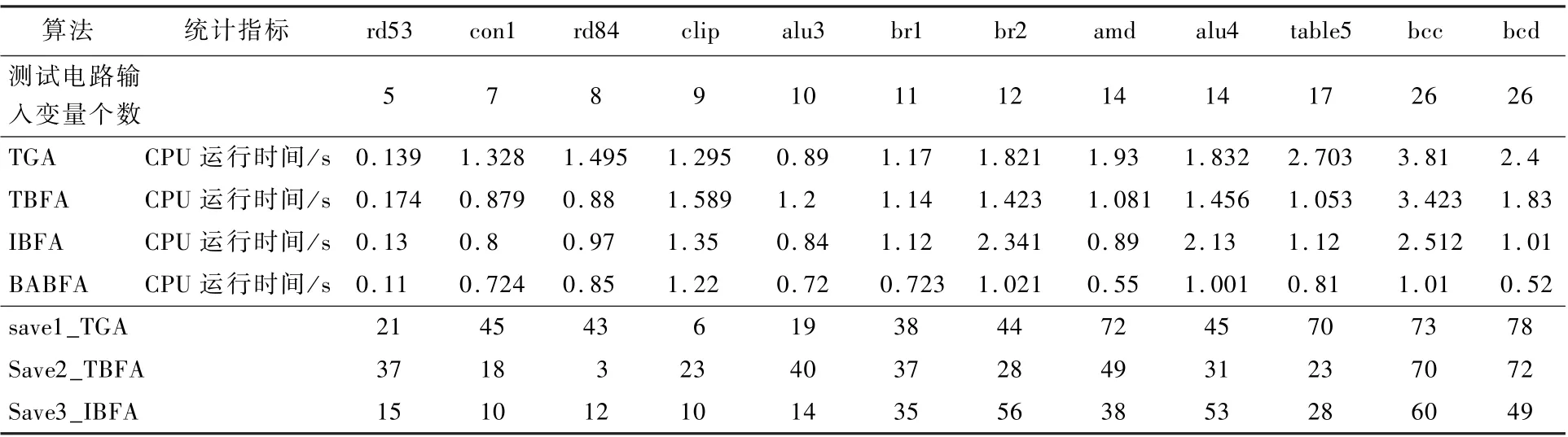
表4 四种算法在时间上的实验结果Table 4 Experimental results of four algorithms on time
4.3 收敛性对比
为了更好地观察BABFA 的搜索性能,将其中4 个测试电路在迭代过程中面积最优解分别进行累加求平均,绘出面积性能优化曲线,纵坐标为运行10 次测试电路面积的平均值,如图4 ~图7所示。 可以看出,相比于其他3 种算法,BABFA能够在迭代次数最小的情况下,寻优速度最快且找寻的面积最优。
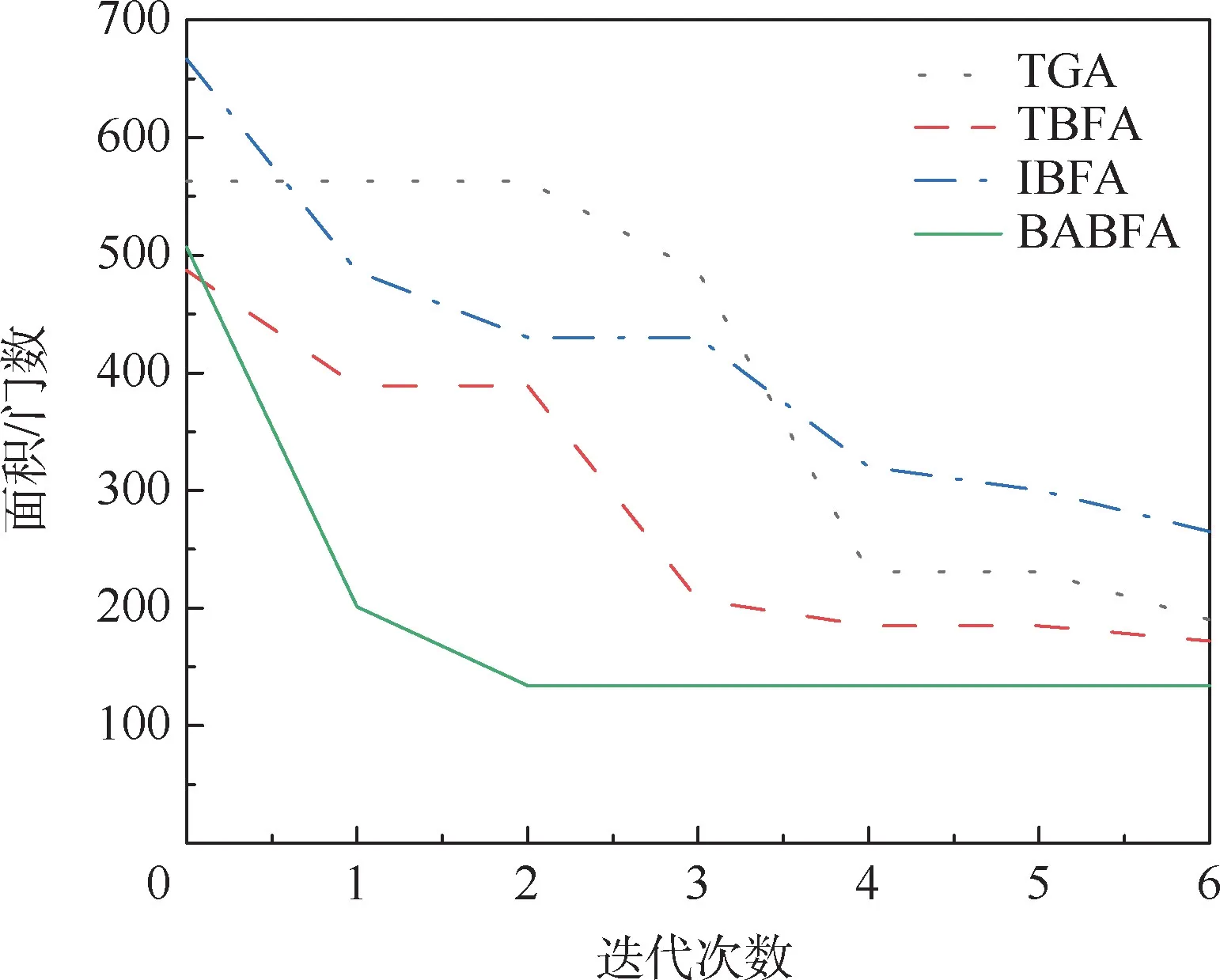
图4 br2 电路最小面积优化曲线Fig.4 Optimization curves of minimum area of br2 circuit
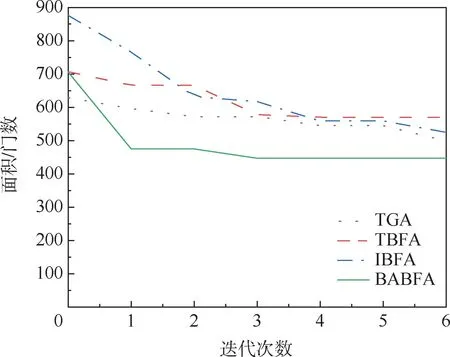
图5 amd 电路最小面积优化曲线Fig.5 Optimization curve of minimum area of amd circuit
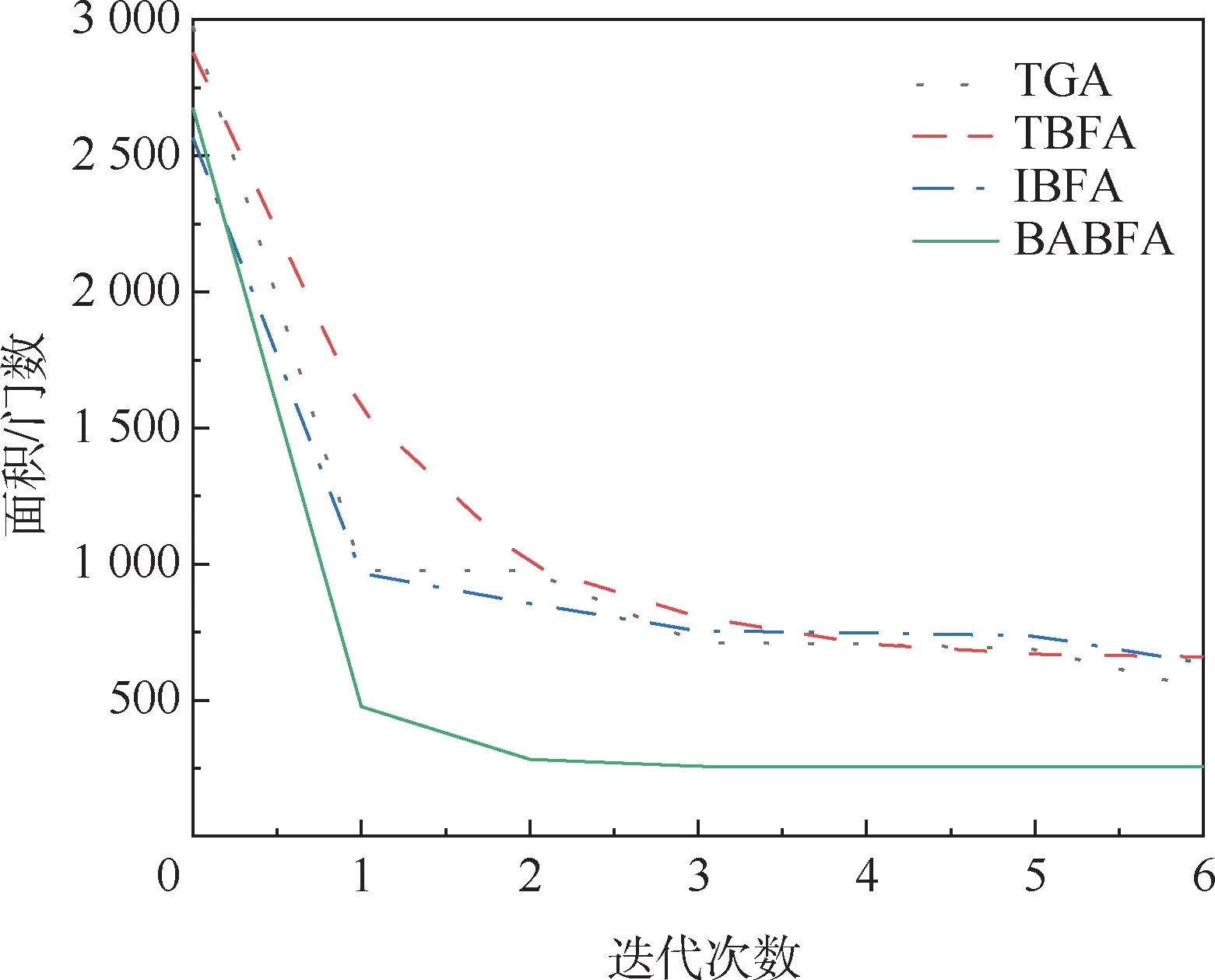
图6 table5 电路最小面积优化曲线Fig.6 Optimization curve of minimum area of table5 circuit
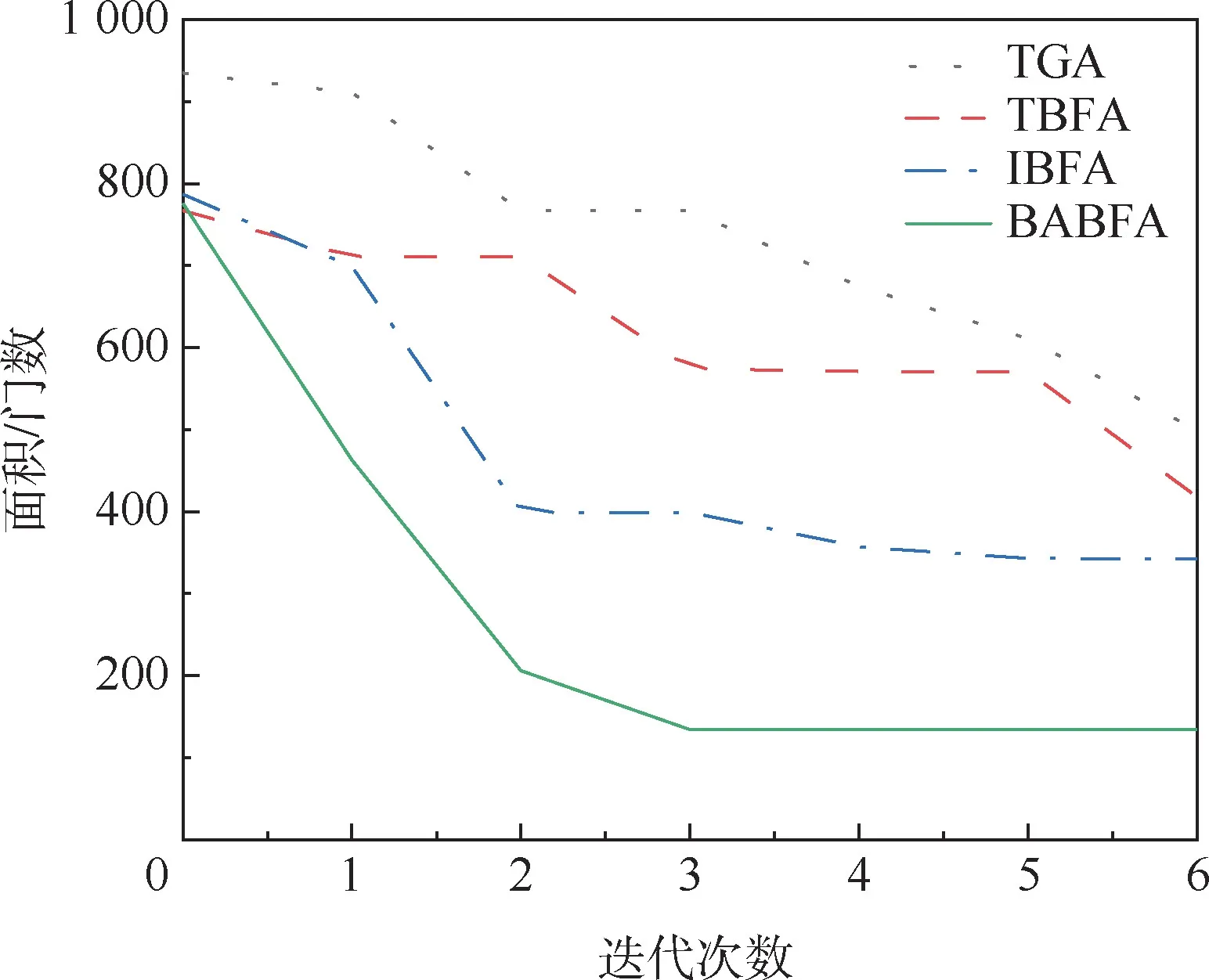
图7 bcc 电路最小面积优化曲线Fig.7 Optimization curve of minimum area of bcc circuit
5 结 论
本文提出了一种二进制自适应细菌觅食算法(BABFA)用于求解基于XNOR/OR 的FPRM 电路面积优化问题。 主要结论如下:
1) BABFA 用于求解二值变量的组合优化问题。 BABFA 在复制操作中添加了复制概率,提高种群的多样性,采用二进制自适应规则对复制率和迁移率进行修正,并且使细菌在半径范围内进行搜索,替代细菌的群体感应机制中的斥力操作。
2) 提出基于XNOR/OR 的FPRM 电路面积优化方法,使用BABFA 来搜索电路面积最小的FPRM 电路。 这是有效的将BFA 应用于RM 逻辑电路极性优化。
3) 基于MCNC 测试电路的实验结果表明,在电路逻辑优化中,BABFA 相比较于其他3 种优化算法,平均面积优化率为15%,平均时间节省率为38%。
