多级降压调节阀内部流动特性数值模拟
2022-11-09方毅芳项高翔唐春娥石月娟
方毅芳 项高翔 唐春娥 石月娟
(1. 机械工业仪器仪表综合技术经济研究所, 北京 100055;2. 西北工业大学 力学与土木建筑学院, 西安 710129; 3. 吴忠仪表有限责任公司, 吴忠 751100)
目前,高压调节阀在多个工业领域均得到了广泛的应用,在整个工业管路控制系统中起着关键的作用,是保证系统安全、经济运行的重要设备之一[1]。 随着工业生产过程向大型化和精细化发展,对高压调节阀也提出了更高的要求。 在高压差下,普通调节阀很难同时满足调节压力和流量的需求,而且高速流体流经阀门时可能出现闪蒸、空化、强振动和高噪声等现象,严重影响调节阀的工作性能和安全使用寿命[2]。 因此,掌握高压调节阀的内部流动特性是调节阀高效应用的前提。
多级降压调节阀采用多级套筒式结构,在阀门结构中,高压流体每经过一个节流截面均会产生一定的压降,将单级阀门中的压力突变转化为压力渐变,压降被多级节流元件分摊,对于不可压缩流体可以防止闪蒸和空化现象的出现,还可以起到降噪和减振的作用[3]。
降压调节阀内部流动为典型的高速湍流,流体经过节流元件时产生剧烈的压力脉动,同时会诱发流体激振并产生高噪声,针对降压调节阀的流动特点,国内外研究人员已经开展了相关的研究。 Franzoni 等[4]以水为工作介质采用多维计算流体动力学(CFD)方法分析了典型元件中的空化现象,讨论了阀座形状对汽蚀发生、压力分布和流量系数的影响。 Bernad 和Susan-Resiga[5]采用CFD 方法对阀门内部流动开展了数值模拟,先对单相流动(液体)进行了研究,定量描述了阀门内部的漩涡流动,再采用全空化模型开展了两相流动(空化)研究。 Zaryankin 等[6]给出了阀箱、扩散器阀座下游和后续蒸汽管线中的压力脉动数据,研究结果表明,脉动水平主要取决于蒸汽进口流路的几何特征。 Shin[7]建立了压力控制阀及其后连接管的数值模型,在此基础上开展非稳态数值计算,分析了阀门及管路内部压力、温度和速度变化的瞬态流动特性。
项美根和孙晓霞[8]介绍了用多级降压法消除电厂调节阀汽蚀的具体方法及现场使用情况,表明采用多级套筒可以明显降低汽蚀发生的可能性,阀门全开时,采用1 级或2 级套筒即可避免空化的发生,阀门开度较小时,需要通过3 级或更多级的套筒消除汽蚀。 蒋玲[9]介绍了一种多级降压高压差结构在放空环境下的应用,通过多级降压结构设计可以达到严密关闭、切断流体、降噪、降压的效果。 顾成果[10]对比分析了不同套筒调节阀的特点。 王燕等[3]应用Fluent 对各套筒结构调节阀内部流动进行了数值模拟计算,适当增大级间间隙或减小套筒上孔径尺寸均有利于高压差调节阀的消声减振。 徐晓刚等[11]针对高温高压降调节阀建立了流场模型及噪声计算模型,研究结果表明,高压降调节阀内采用多级消声节流套筒可有效实现逐级降压、限制流速和抑制噪声的目的。 彭健和何世权[12]采用数值计算方法对阀门内部的汽蚀现象进行了仿真研究,发现阀门处于小开度下容易产生汽蚀,汽蚀部位主要位于节流孔的阀芯与阀座处。 李树勋等[13-14]针对多级套筒式降压疏水阀开展了流激振动和流致噪声的数值研究,研究数据表明,不同开度下阀门的振动特性主要由阀内节流件结构决定,受开度的影响较小,中等开度下阀门的振动最小,套筒内节流区的流体压力脉动最强,不同套筒结构参数的调节阀噪声频谱均呈现明显的宽频特性。
总体来看,目前研究多集中于单级或双级套筒降压调节阀,对于不同开度下多级套筒结构降压调节阀内部流动特性的研究较少。 本文在总结现有公开研究成果的基础上,以多级降压调节阀为研究对象,建立调节阀的三维计算模型并采用CFD 数值方法计算不同压差及不同开度条件下阀门的内部流动,分析不同压差及不同开度下各级套筒及阀座的压降及其对阀内空化的影响,为降压调节阀的合理设计提供理论依据和参考。
1 数值计算模型及方法
多级降压调节阀由于其内部结构复杂,进出口压差大,流体在阀内的高速流动过程中容易产生剧烈的压力脉动,进而导致阀体内部流动出现空化现象。 常见的实验设计[15-16]仅能测量阀门进、出口压差和流量等统计参数,对于阀门内部流动的复杂过程难以定量地描述和研究。 因此,本文中数值计算的优势得以体现:通过阀体建模及网格划分,可计算获得不同边界条件下多级降压调节阀内部的流动特性及空化特征。
1.1 数值计算模型
1.1.1 湍流模型
随着计算流体动力学的深入发展,当前的湍流计算模型主要分为以下4 种:直接数值模拟(DNS)、雷诺平均Navier-Stokes 方程(RANS)、大涡模拟(LES)和分离涡模拟(DES)。 湍流场中存在尺度差异较大的涡,且不同尺度的涡之间存在复杂的相互作用,因此,RANS 方法难以较好地模拟降压阀内部的复杂流动。 尽管DNS 及LES 方法可以很好地捕捉涡结构,但其计算量过大,计算时间消耗过长。 本文最终选取DES 方法中的改进延迟分离涡(IDDES)开展数值模拟,该模型在计算精度和效率上可以满足工程需要。
在DES 方法中,边界层采用非定常RANS 模型,分离区域采用LES 处理。 LES 区域通常与较大的非定常湍流尺度起主导作用的核心湍流区域相关联。 在上述区域,DES 模型采用了类似于子网格模型的LES 方法。 而在近壁面区域,恢复了相应的RANS 模型。
IDDES 方法[16-17]为延迟分离涡流模拟(DDES)与壁面模型LES 方法(WMLES)的耦合算法。 与DES 相似,对基准模型/湍流剪应力输运模型(BSL/SST)的k方程进行了修正,加入了局部网格间距的信息。 当来流条件湍流较强并且网格尺度能够分辨边界层主导的旋涡结构时,模型将切换到RANS 和LES 混合模式,具体实现方法如下:
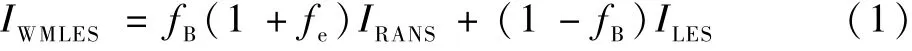
式中:IWMLES为壁面模型长度尺度;IRANS和ILES分别为RANS 和LES 的长度尺度;fe为提升函数;fB为经验混合函数,表达式为
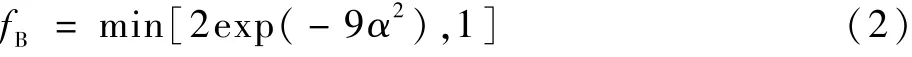
式中:经验系数α=0.25 -dw/hmax,dw为当地网格到壁面的距离,hmax为当地网格在3 个空间方向上的最大尺寸。
经验函数fe用于避免RANS 与LES 交界区域Reynolds 应力的过分衰减,解决对数层不匹配问题。 当RANS 和LES 交界面非常接近壁面时,Reynolds 应力可以忽略。
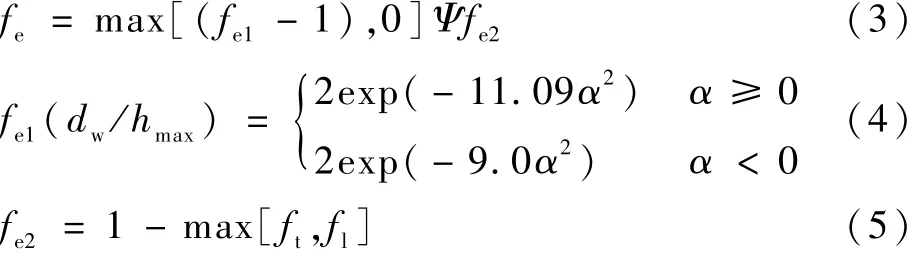
式中:Ψ为特征函数;参数ft和fl可以控制模型中RANS 模型部分的强度,其大小也由经验参数控制。 当在附面层内时,通过选择合适的参数保证ft或fl中的一个值接近于1,从而fe2和fe接近于0,使得RANS 和LES 可以在附面层附近相互平滑切换。
为了将DDES 模型和WMLES 模型的长度尺度进行混合,需要对DDES 模型的长度尺度进行修改,如下:
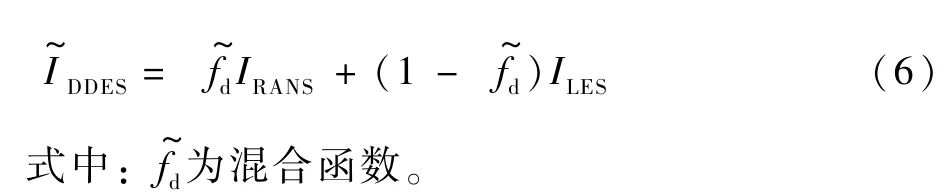
来流包含湍流成分时,IDDES与IWMLES接近,数值模拟可以分辨边界层主导的湍流流动。
1.1.2 两相流模型
两相流模型中的Mixture 模型[18-19]是一个简化的多相模型,该模型可以用来模拟不同速度运动的多相流,在较短的空间长度尺度上假设局部平衡,也可用来模拟具有很强耦合和相同运动速度的多相流,最后根据混合模型计算非牛顿黏度。
Mixture 模型可以通过求解混合物的动量、连续性和能量方程、第二相的体积分数方程和相对速度的代数表达式来模拟流体或颗粒相。

式中:g为重力加速度;αk为第k相的体积分数;ρk为第k相的密度;n为相序号;F为体积力;μm为混合物黏性;vdr,k为次级相k的漂移速度。
1.1.3 空化模型
Shabil[20]推导了从液体到蒸汽净质量输运的精确表达式。 蒸汽体积分数的方程式一般形式为

式中:ρ为混合物密度;ρl为液相密度。
式(11)可将蒸汽体积分数与每单位体积液体的气泡数关联:

式中:R为质量输运率;Rb为气泡半径;Pv为饱和蒸汽压;P为气泡的压力;n为气泡数密度。
1.2 计算对象及边界条件
本文计算对象为某多级降压调节阀,如图1所示。 其中,各级套筒及阀座由左侧入口到右侧出口级数依次定义为i(i=1,2,3,4),因为流经各级套筒及阀座会对工质产生一定压降,所以将该级定义为第i降压级。
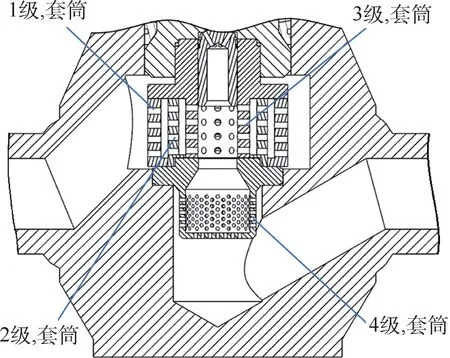
图1 多级降压调节阀剖视图Fig.1 Sectional view of multi-stage pressure drop valve
使用CAD 软件提取出降压调节阀的三维流体域模型,三维流体域计算模型如图2 所示,其中最左侧管道截面为阀门入口,边界条件设置为压力进口;最右侧管道截面为阀门出口,边界条件设置为压力出口;阀体壁面边界条件设置为壁面,内部流体计算域边界条件设置为流体。
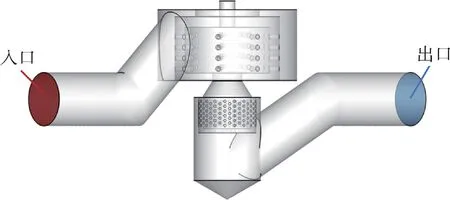
图2 多级降压调节阀流体域模型Fig.2 Fluid domain model of multi-stage pressure drop valve
多级降压调节阀的进出口压力(表压)及压差如表1 所示。
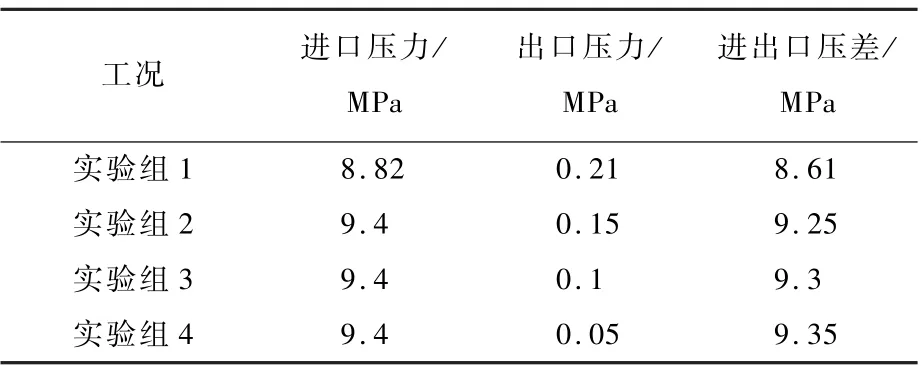
表1 不同工况条件实验组阀门的进出口压力及压差Table 1 Inlet and outlet pressures and pressure differe under different conditions
1.3 计算网格及计算方法
在建立多级降压调节阀结构模型的基础上,对多级降压调节阀进行了网格划分,由于多级降压调节阀中的进出口流道及套筒中间流道的尺寸和各级套筒小孔孔径差异较大,且多级套筒结构复杂,对多级降压调节阀整体均采用四面体网格进行剖分,在保证网格质量的同时可方便控制阀内不同位置的网格疏密程度,最终确定数值计算所用网格数量为1 200 万。 图3 与图4 分别给出了多级降压调节阀结构整体和局部的网格划分情况。
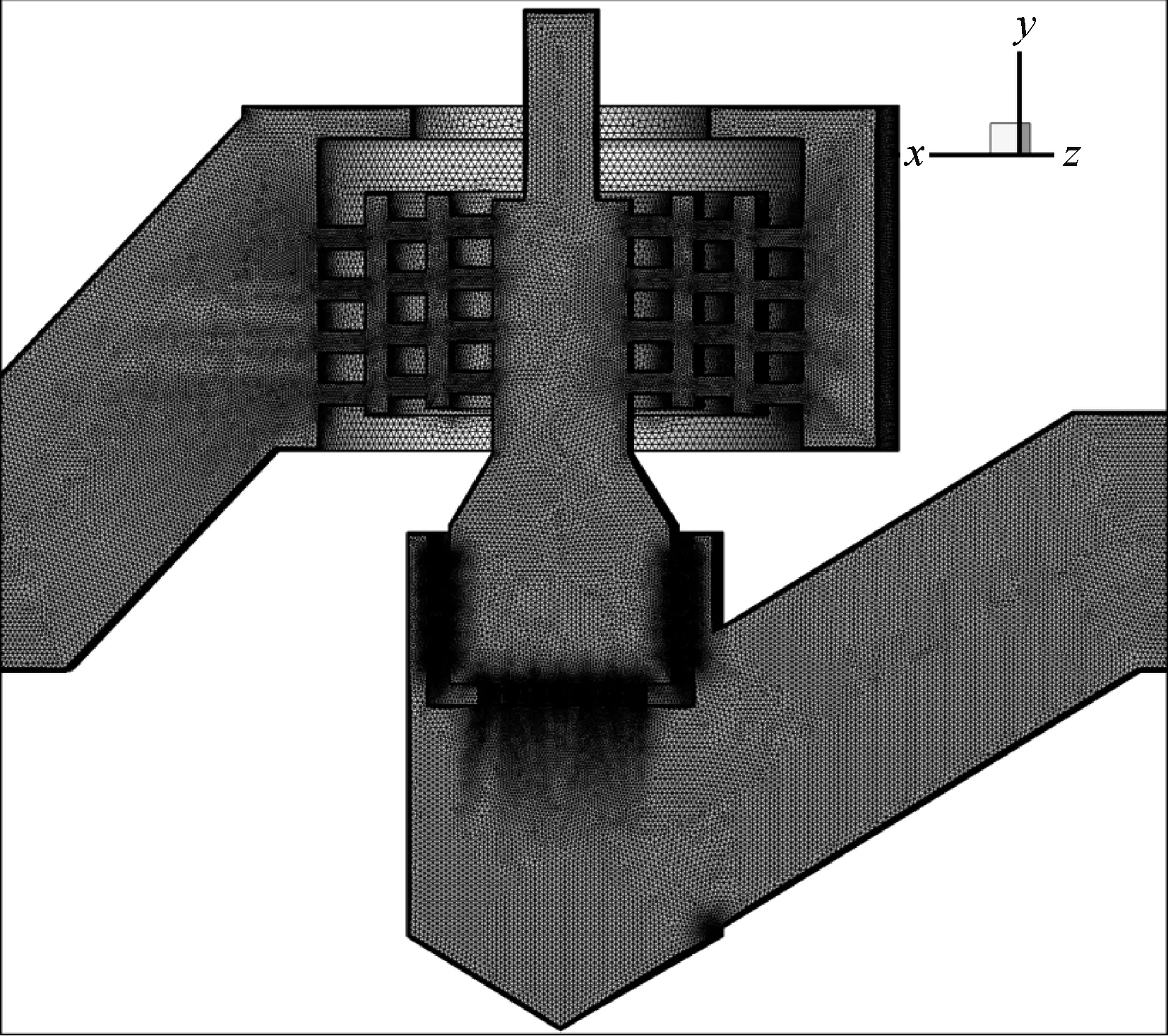
图3 多级降压调节阀的整体网格划分Fig.3 Integral meshing of multi-stage pressure drop valve
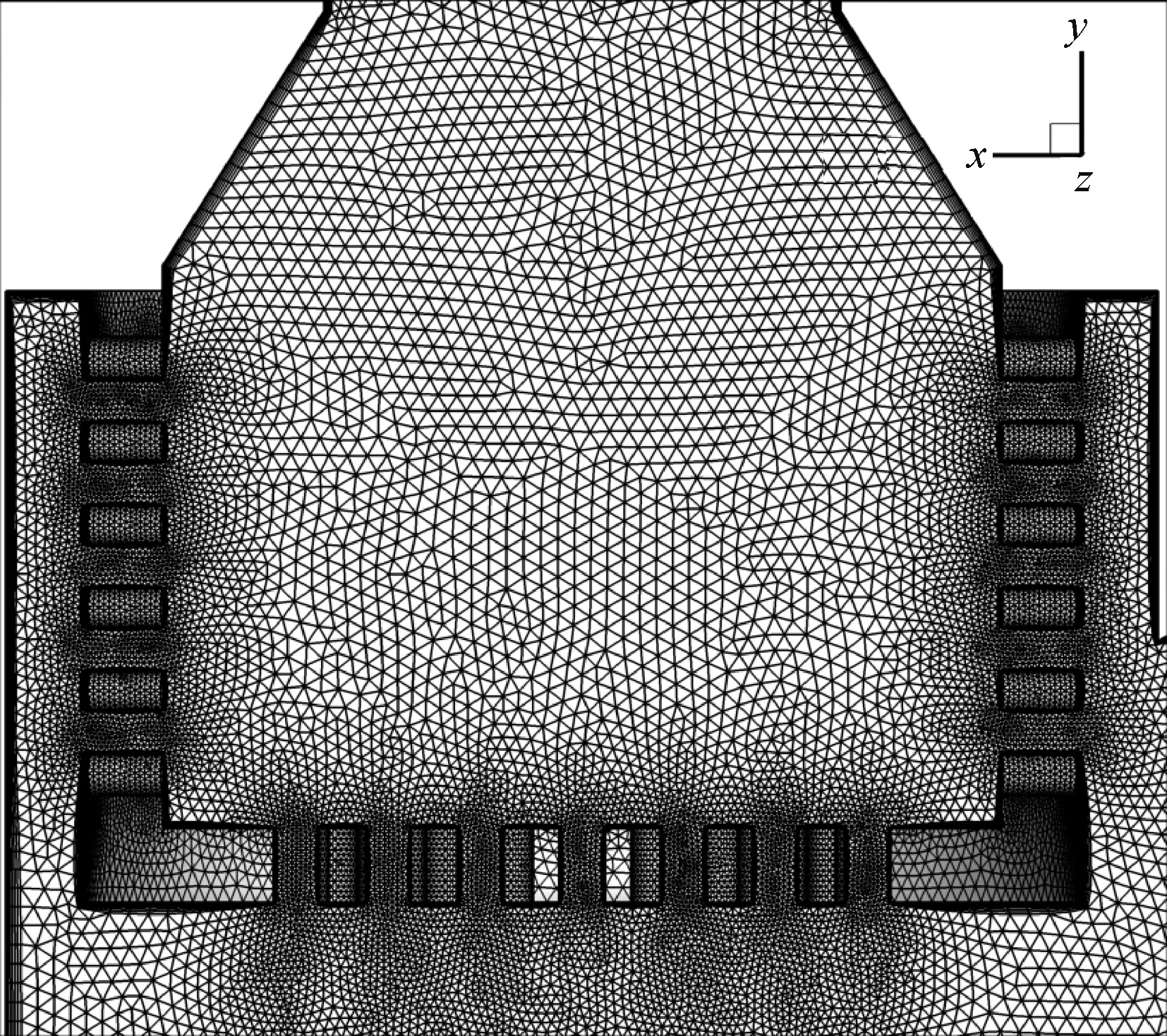
图4 多级降压调节阀的局部网格划分Fig.4 Local meshing of part of multi-stage pressure drop valve
为分析多级降压调节阀内部的流动特性,确定了本文所采用的数值计算方法,如表2 所示。
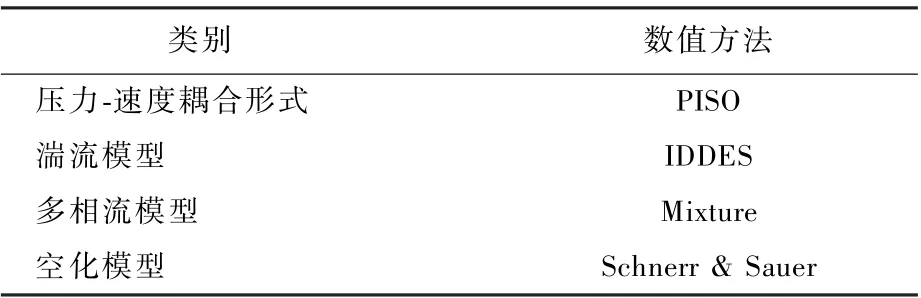
表2 关键数值计算方法Table 2 Key numerical calculation methods
在数值模拟中,计算网格的尺寸和数量会影响数值计算结果的准确性。 网格数量较少时可能导致计算结果与精确解间存在较大的计算偏差,当网格数量不断增加至某一数量后,数值计算结果逐渐趋于稳定并相对可靠,但是所需计算资源也不断增加。 为了确定合适的网格数量,选取网格数分别为732.6 万、1 203 万和1 758 万进行网格无关性验证,不同网格数量对应的阀门质量流量如表3 所示。 随着网格数量的增加,阀门流量逐渐趋于稳定,图5 给出了不同网格数量下阀门中心线上的压力分布。 由图5 可以看出,不同网格数量的计算结果间差异均较小,M3 与M2 计算结果的偏差很小,在保证精度偏差可接受的前提下,综合考虑计算时间和效率等因素,最终选择了包含1 200万网格单元的方案,可以较好地捕捉阀门内部的流动过程。
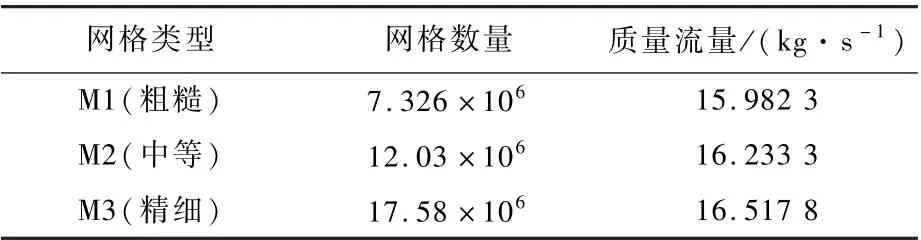
表3 网格类别Table 3 Mesh specifications
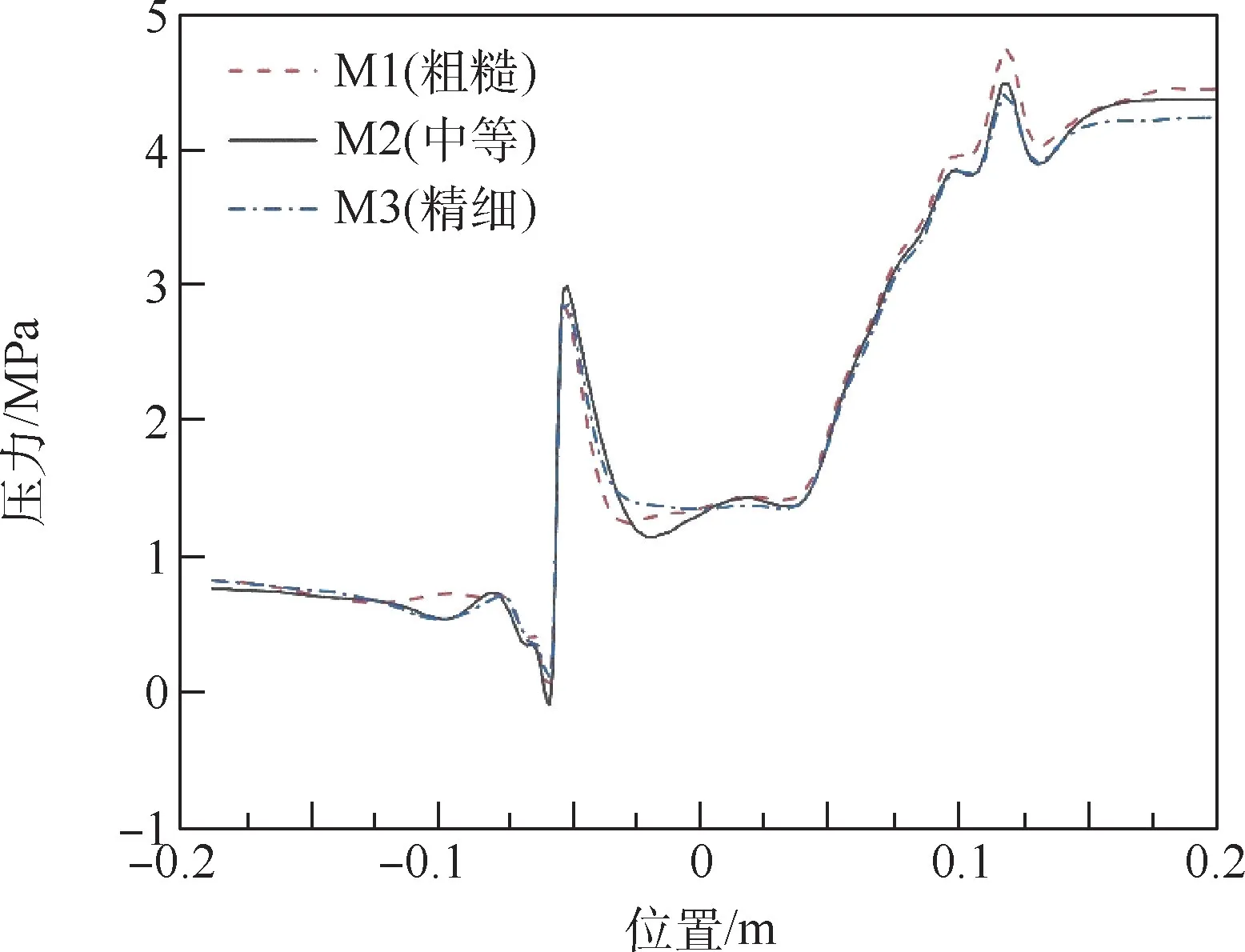
图5 阀门中心线上压力分布Fig.5 Pressure distribution at the median of valve
2 数值计算结果
2.1 调节阀内部流场分布
在建立完整数值计算模型和数值计算方法的基础上,通过数值模拟计算,图6 和图7 分别给出了实验组1 工况下多级降压调节阀处于半开时中间截面的压力和速度分布。 当流体流经各级套筒和阀座时,由于小孔的节流作用均出现了明显的压差,各级套筒及阀座结构尺寸不同,进而导致各降压级的压降存在一定的差异。 本文中的工质为不可压流体,结合图6 来看,在套筒的小孔处流体加速流动,流速远大于阀门其他位置处的流动速度,流体通过小孔后又流入流通面积较大的空间,高速流体冲击套筒壁面在套筒间存在剧烈的碰撞,形成复杂的湍流流动。 当流体沿第3 级套筒周向分布的小孔进入中间阀芯时,多股流体产生强烈地掺混和剪切,同时还需改变流动方向进入阀座,高速流体流过阀座也会出现类似的现象,多级降压调节阀内的流动特点导致在其内部形成了大量的漩涡,其内部的湍流脉动冲击会诱发阀门的振动和噪声。 阀门内部的涡量分布如图8 所示,Q为速度梯度张量的第二不变量,正值表示流场中涡量占主导的区域,负值表示应变速率或黏性应力占主导的区域。 可以看出,阀门进口段的漩涡较少,经过各级套筒和阀座后的漩涡急剧增加,不同流体微团之间相互掺混使得流体能量得以耗散,阀座后形成的漩涡进一步逐渐发展至阀门下游出口段中。
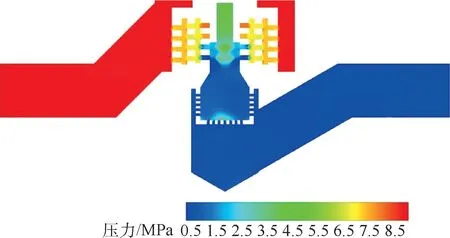
图6 阀门中间截面的压力分布(实验组1)Fig.6 Pressure distribution at the middle section of valve(case1)
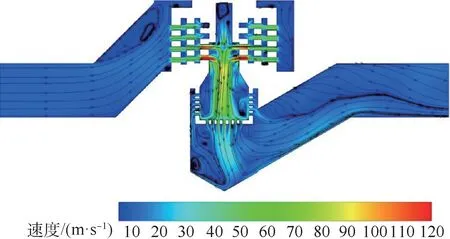
图7 阀门中间截面的速度分布(实验组1)Fig.7 Velocity distribution at the middle section of valve(case1)

图8 阀门内部的涡量分布(Q =1)Fig.8 Vortex distribution inside valve(Q =1)
图6 中,50%开度条件下第3 级套筒处的压降接近6.0 MPa,小孔处的最高流速达到120 m/s,高压差引发高速流动的情况下极易产生空化现象。图9 为多级降压调节阀中间截面的气相分布。 第3 级套筒的小孔和阀座部分小孔处均出现了明显的空化现象,且第3 级套筒下侧小孔处气体体积较大,表明该处的空化程度较强;阀座处的所有小孔几乎均发生了空化,但每个小孔表面的气相体积分数较小,整体而言,阀座比套筒更容易产生汽蚀,但空化程度较弱。
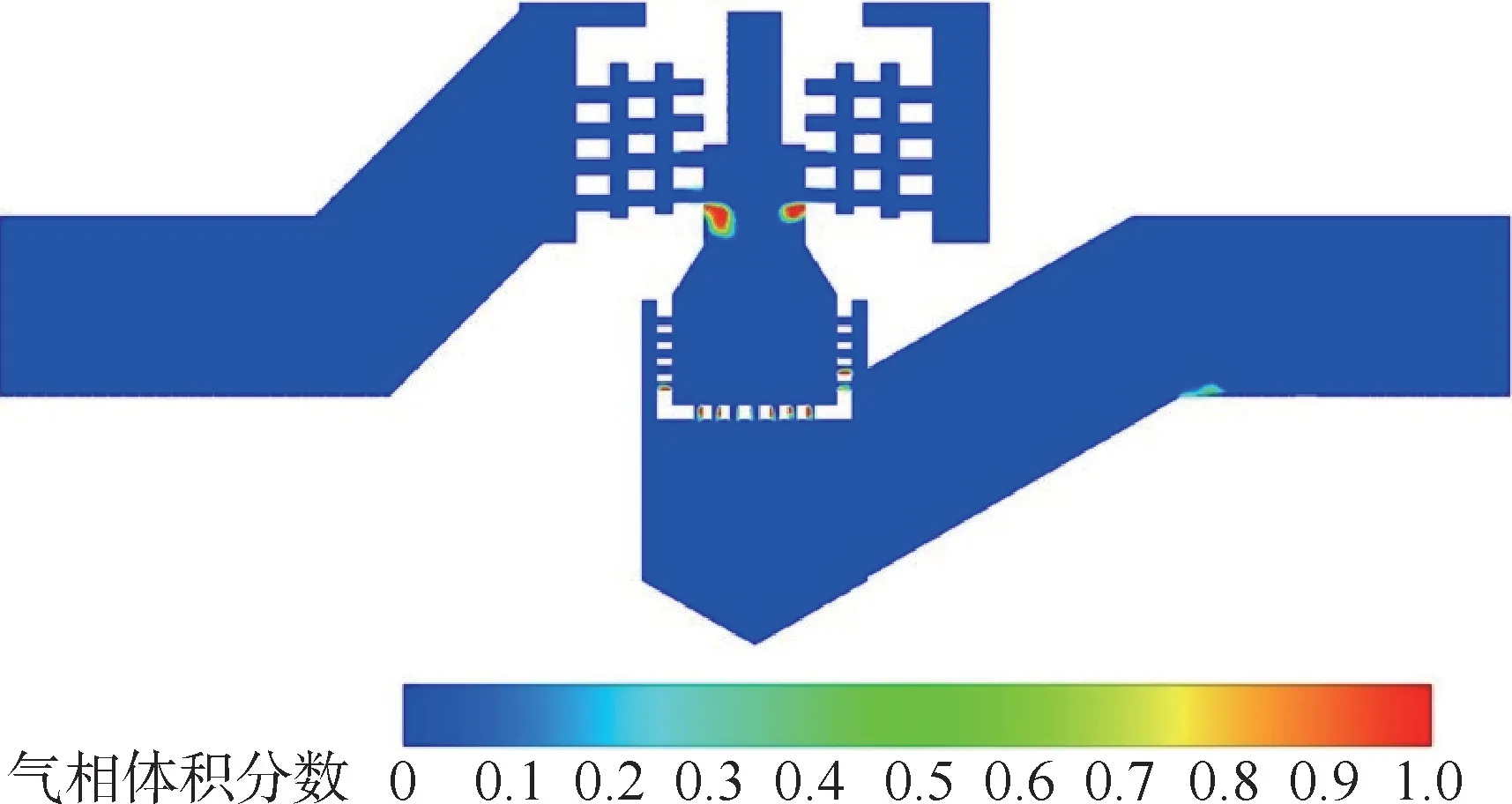
图9 阀门中间截面的气相分布(实验组1)Fig.9 Vapor distribution at the middle section of valve(case1)
图10 为实验组1 工况下多级降压调节阀进口质量流量随不同开度的变化。 在节流较大的小流量范围内,阀门进口质量流量几乎呈线性增加,随着开度的逐渐增加,质量流量的增加趋势逐渐减小。
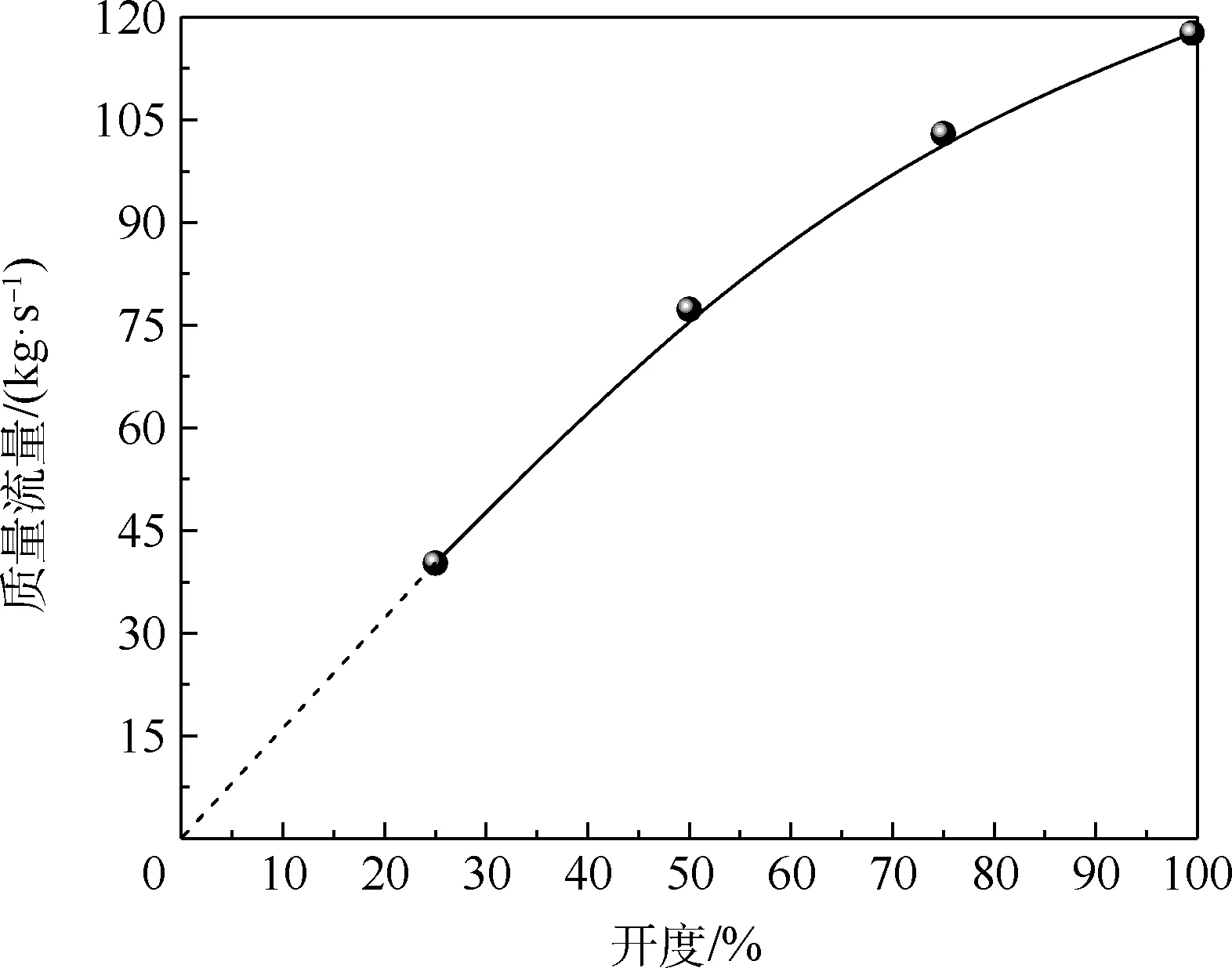
图10 阀门进口质量流量随开度的变化(实验组1)Fig.10 Mass flow rate at valve inlet versus valve opening degree(case1)
2.2 不同压差下调节阀流动特性分析
阀门在不同的进出口压力条件下,多级降压调节阀的流动特性会产生一定的变化。 对于不同开度的降压调节阀模型,不同开度工况下工质流经各降压级的压降如图11 所示。
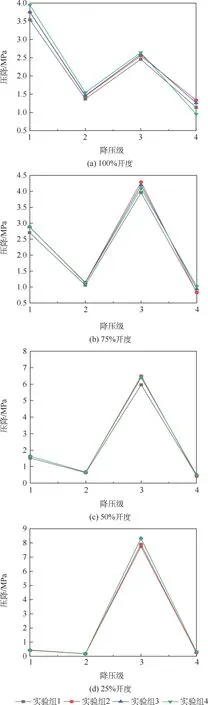
图11 不同开度下的压降变化Fig.11 Variation of pressure drop under different opening degree
由图11(a)可知,在开度为100%的工况条件下,工质流经各降压级的压降振荡较低,且变化趋势基本一致。 压差越大,工质流经第1、2 和3 降压级的压降就越大。 对于实验组2、3、4 来说,3种工况下的进口压力不变但背压降低,可以看出,随着背压降低,前3 个降压级处的压降反而升高,第4 降压级的压降随之降低。
在阀门开度为75%的工况下,各降压级的压降曲线变化趋势一致,均在第3 降压级最高,第1降压级次之,而第2 和4 降压级较低。 在阀门75%开度下,对于实验组2、3、4,第1、2 降压级处的压降重合,即此处压降受到进口压力影响较大,而几乎不受到背压的影响。
当开度继续降低至50%时,由图11(c)看出,所有工况在第2、4 降压级处的压降几乎一致, 实验组1 工况下阀门的进出口压差较小,从而其在第1、3 降压级的压降相对其他工况较小。
当开度为25%时,由图11(d)可以看出,所有工况在第1、2、4 降压级处的压降几乎一致且都极低。 各工况在第3 降压级处的压降受到进出口压差的支配,由图12 可以看出,在该开度下,实验组1工况下的工质压降主要在第3 降压级处发生,同时根据压降曲线可以推知其他工况中均类似。
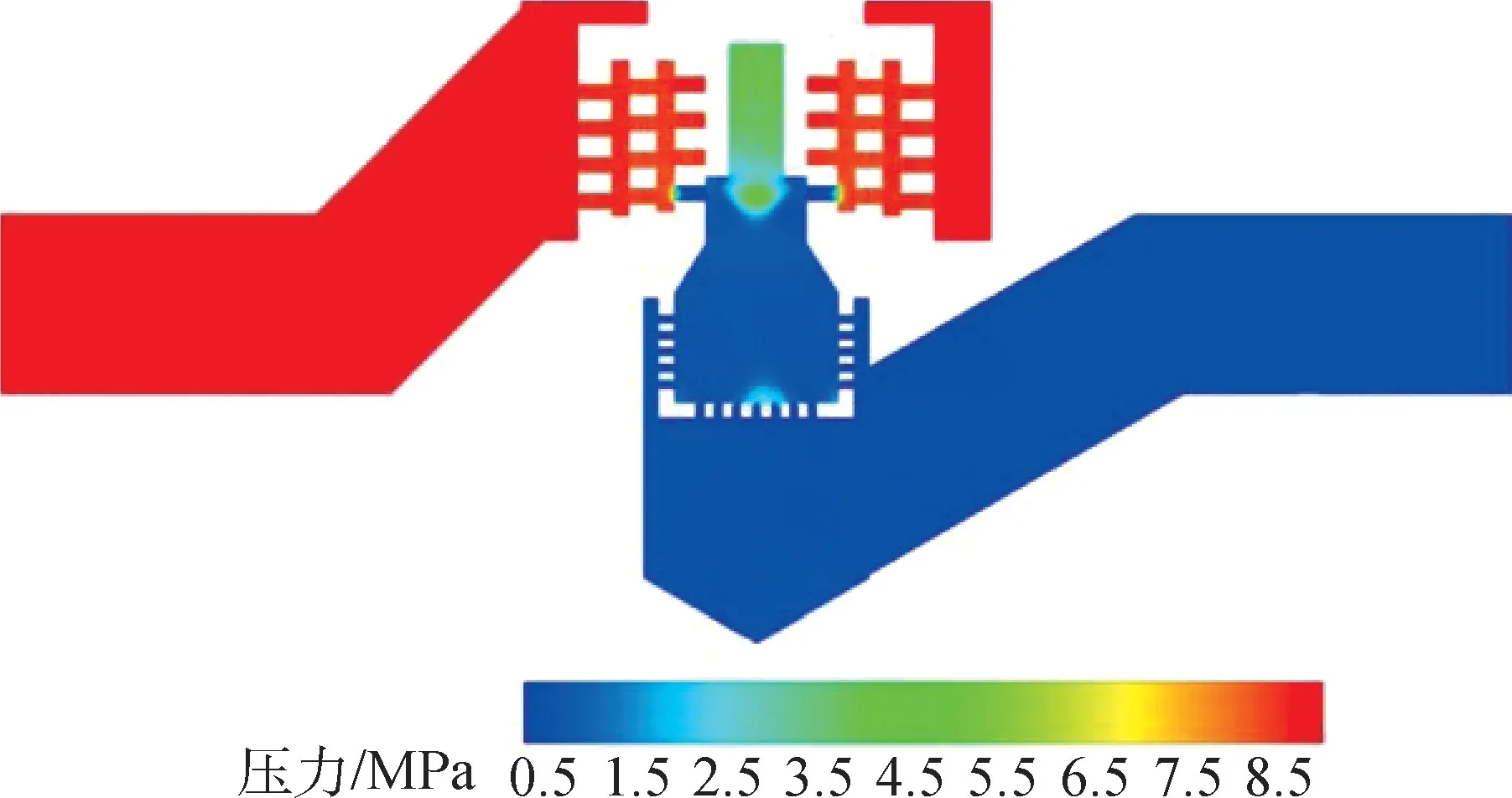
图12 实验组1 的静压分布云图(开度25%)Fig.12 Static pressure distribution of case 1(opening degree 25%)
2.3 不同开度下调节阀流动特性分析
不同开度下,多级降压调节阀在各降压级间的静压分布产生了较大差异。 图12 和图13 给出了不同开度下阀门中间截面处的压力分布云图。
如图13(a)所示,当阀门开度为100%时,在第1 降压级附近静压发生剧烈减小;而在第2 降压级附近没有明显变化;在第3 降压级附近,出现低压区域,故压降应有所增大;在第4 降压级附近,静压产生了少量下降。
当开度为75%时,如图13(b)所示,第1 降压级后段的静压相对图13(a)中的对应位置更高,因此该级压降小于开度100% 的情况;由于第3降压级的一排小孔被堵塞,工质经过该级的流通面积变小,根据连续方程可以得出:工质在流经第3 降压级时加速,因此静压下降更加剧烈;从图14中75% 开度的曲线可以看出,在第3 降压级处75%开度的压降大于100% 开度的压降;由图15可知,阀门在100% 开度条件下的高速区域在第1、2、3 降压级中均有存在,而阀门在75%开度条件下的工质仅在第3 降压级附近有剧烈的加速。
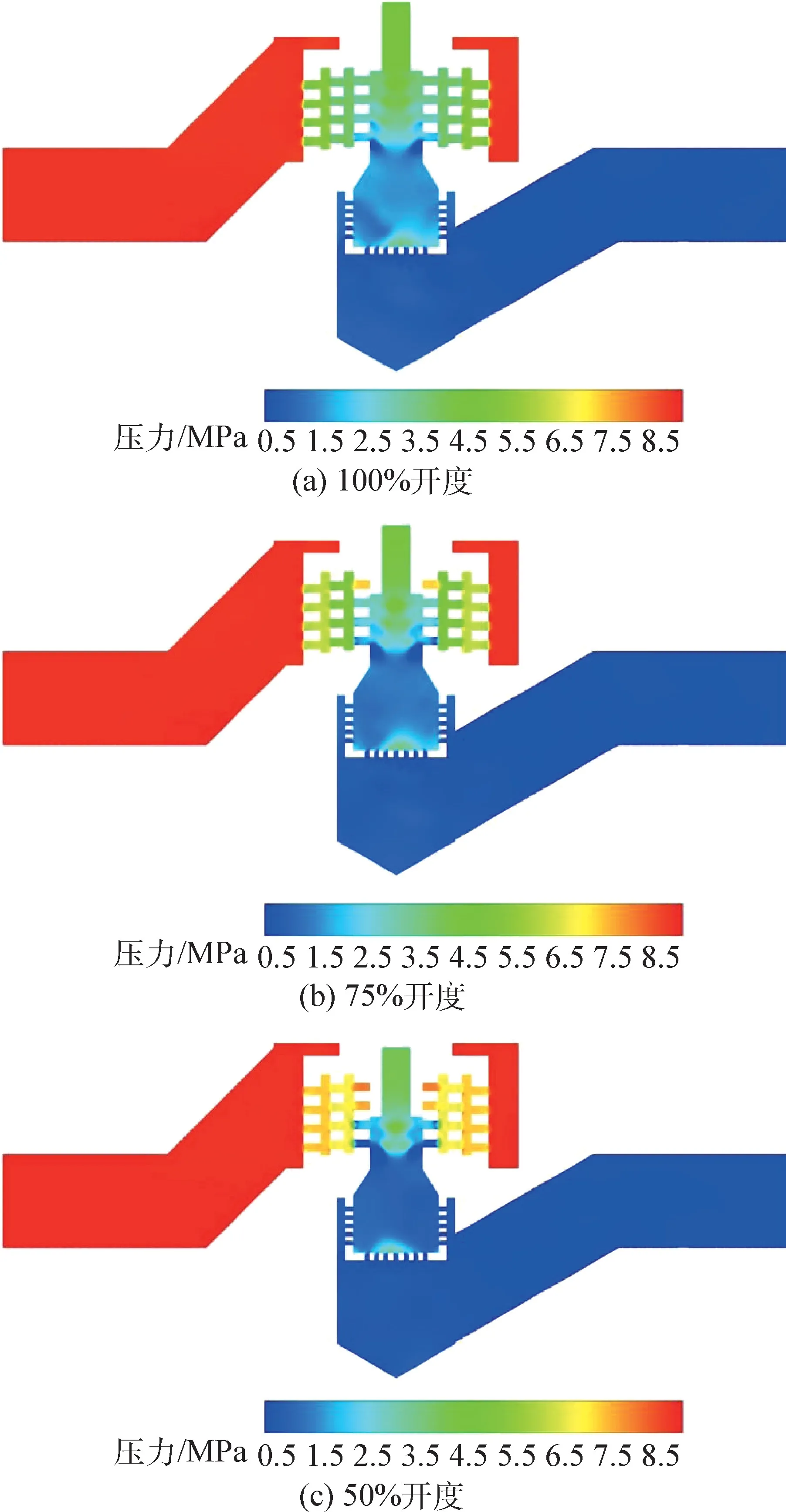
图13 不同开度下实验组1 的静压分布云图Fig.13 Static pressure distribution of case1 under different opening degree
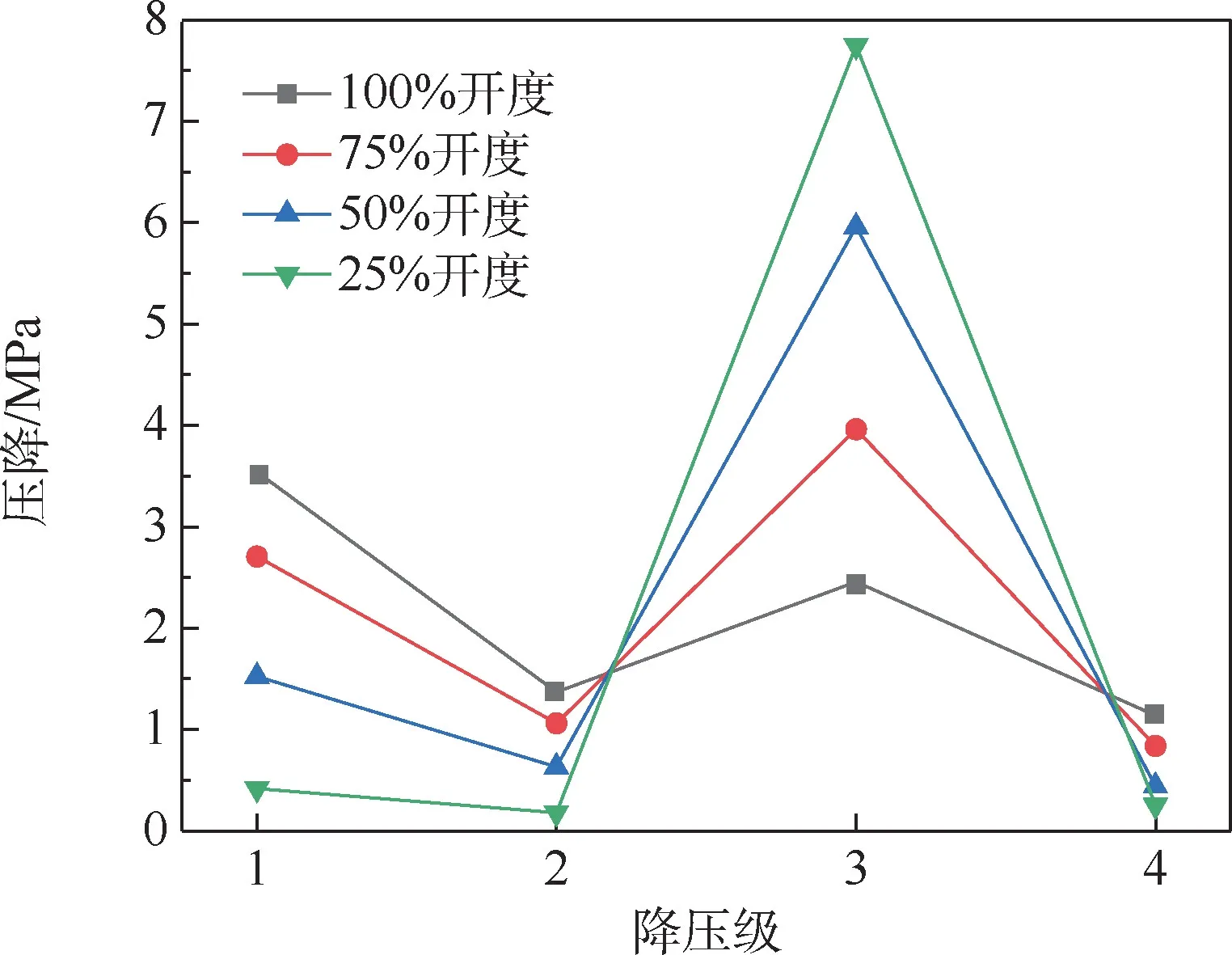
图14 不同开度下降压级的压降变化(实验组1)Fig.14 Pressure drop variation of pressure-descending stages under different opening degree (case1)
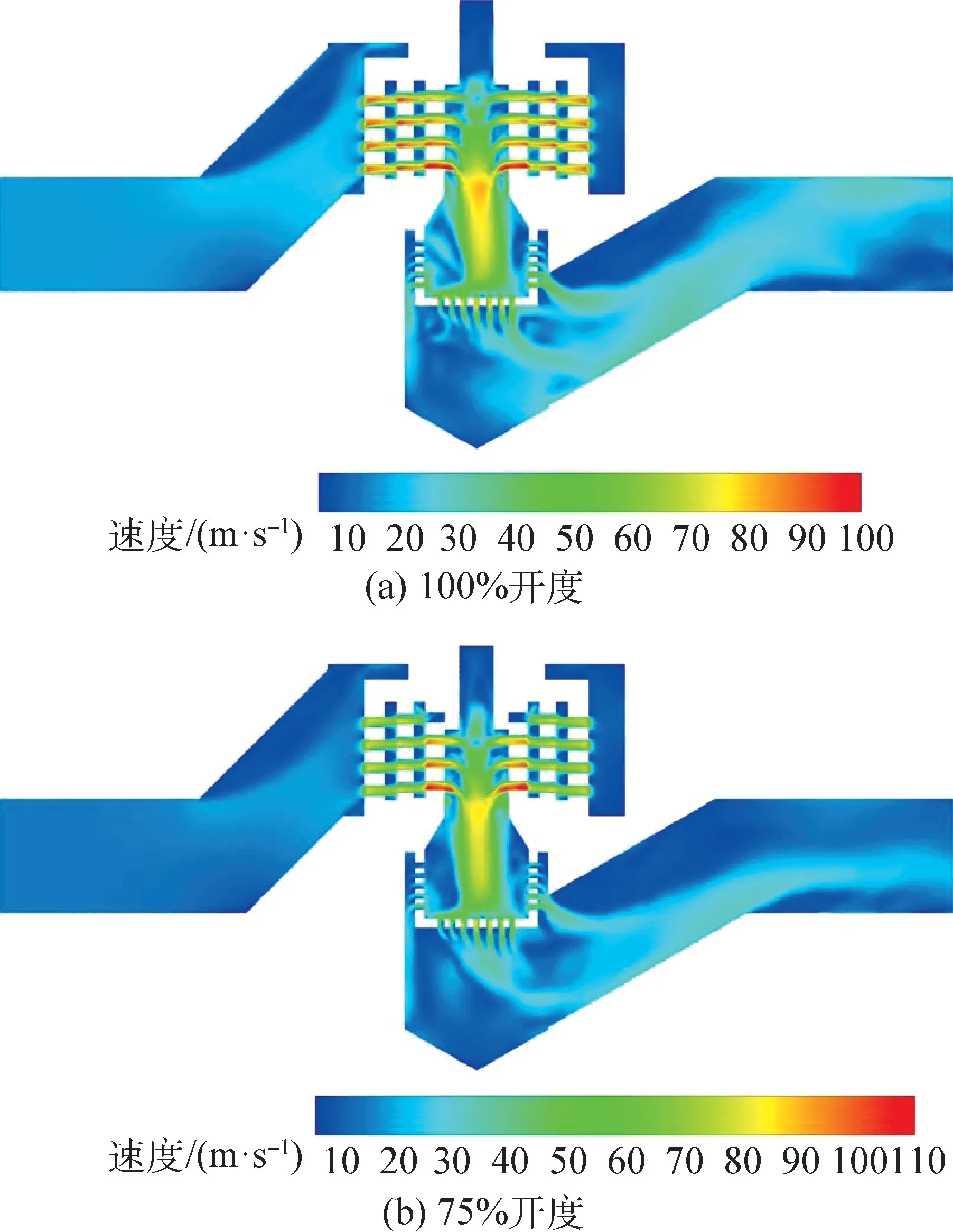
图15 实验组1 的速度分布云图Fig.15 Velocity distribution of case1
由图13(c)和图12 可以看出,随着开度进一步降低,第1、2 降压级附近的静压逐渐升高,而第3 降压级出口段的静压剧烈下降,进而导致该级压降随之增大,观察图14 可得出相似结论。
对于本文研究的其他进出口压力条件的工况,不同开度下降压级的压降变化有着类似的结论,如图16 所示。
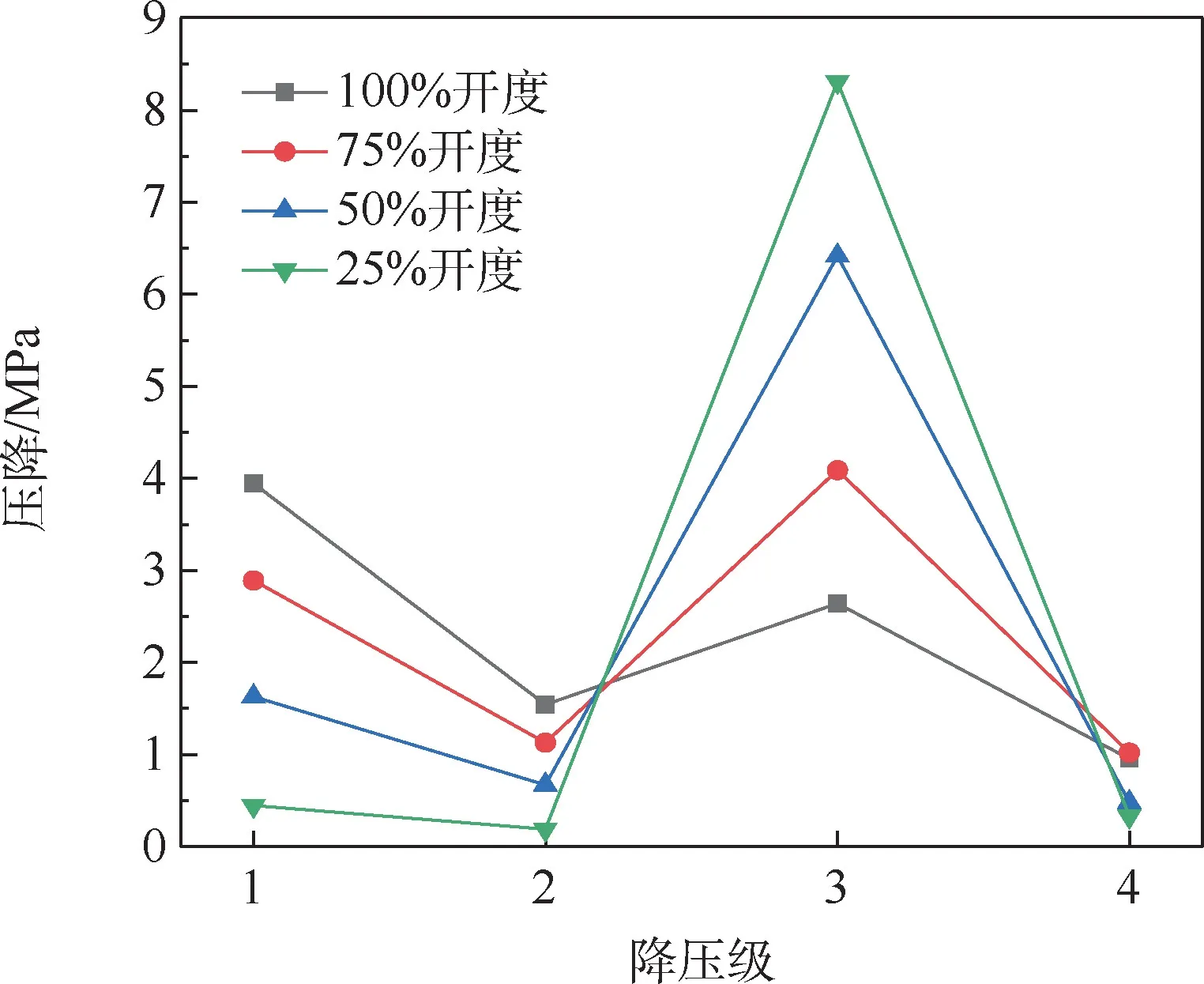
图16 不同开度下降压级的压降变化(实验组4)Fig.16 Pressure drop variation of pressure-descending Stages under different opening degree (case4)
对于第1、2 和3 级降压阀套筒,本文截取了第1 ~3 级套筒圆柱状小孔中心线上的沿程压力和速度分布,如图17 和图18 所示。
从图17 可以看出,各开度下的沿程速度呈现出阶梯状分布,工质流经一级套筒小孔前段附近时,速度产生陡峭的上升,而后平缓地流过该级小孔,并重复这一过程。 与大开度相比,阀门开度越小时,工质流经1 级和2 级套筒的速度增量相对越大,而流经第3 级套筒速度增量相对越小。
对照图17 的速度分布曲线,图18 反映出相应的沿程静压分布情况。 各开度下的沿程静压呈现出阶梯状分布,工质流经一级套筒孔隙前段附近时,由于对应的速度增加,压力产生陡峭的下降,而后平缓地流过该级小孔,同样重复该过程。与大开度相比,开度越小时,工质流经1 级和2 级套筒的压降相对越小,而流经3 级套筒的压降相对越大。
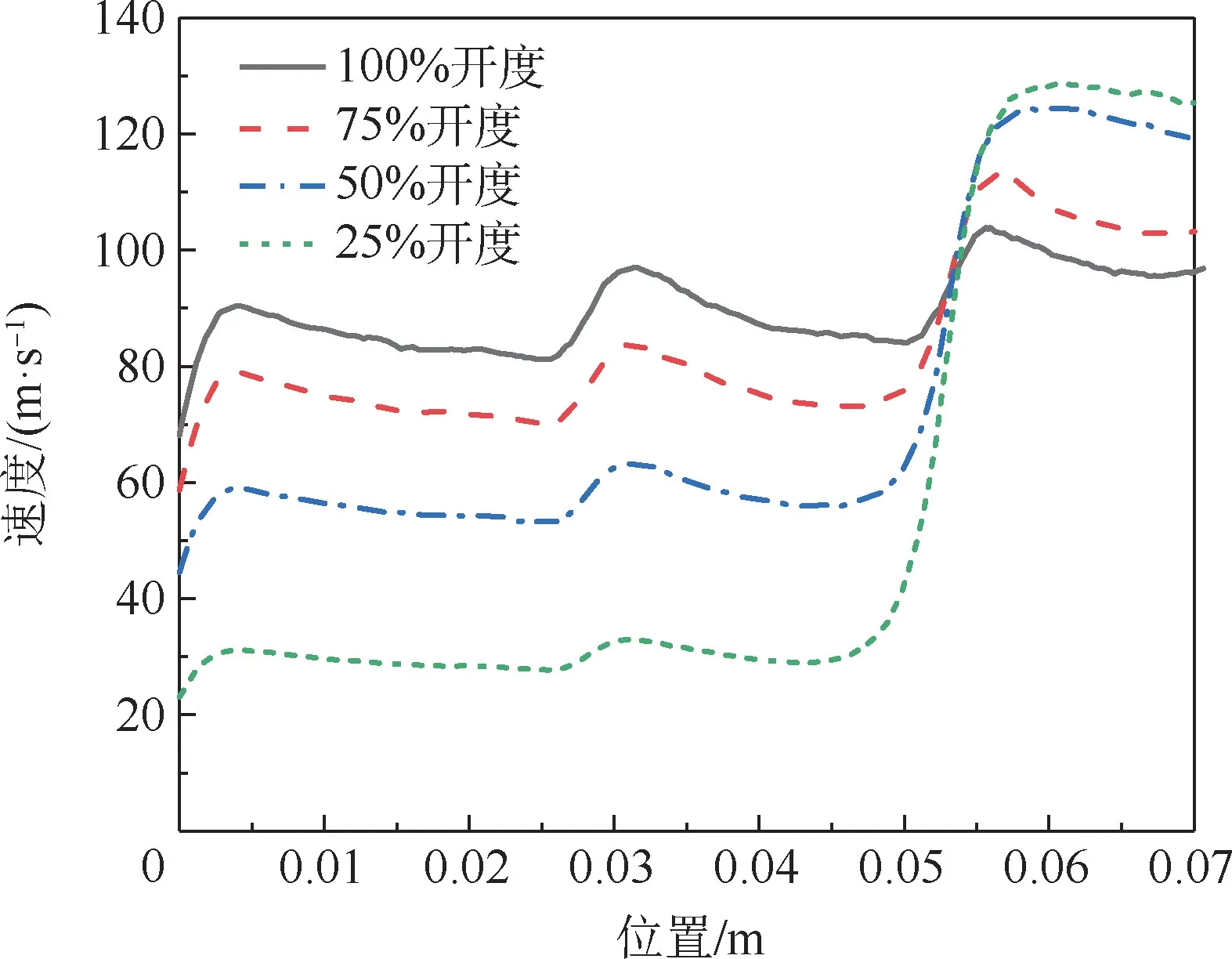
图17 第1 ~3 级套筒沿流向中心线速度分布曲线Fig.17 Velocity distribution curves of the 1st ~3rd stage sleeve along the centerline flow direction
3 结 论
1) 流体流经阀门内节流元件时由于多股流体的强烈掺混和剪切,套筒和阀座下游存在大量的漩涡;各级套筒及阀座结构尺寸不同,各降压级的压降存在一定的差异,第3 级套筒处的空化程度最大,阀座处更易发生空化。
2) 阀门在同一开度下,工质沿各降压级的压降在不同压差下的变化趋势相同。
3) 随着阀门开度的逐渐减小,最大压降由第1 降压级转向第3 降压级,在25%开度下阀门第3 降压级的平均压降达到8 MPa,且第1、2 降压级的压降受到进口压力的主导作用逐渐减弱,第4降压级受到背压的支配作用也逐渐减弱。
4) 第3 降压级的出口面积随阀门开度的减小不断下降,该降压级处的压降随阀门开度的减小而增大,相同流量下该降压级小孔中工质的速度也增加。
本文根据多级降压调节阀的流动特点建立了有效的数值计算方法,计算结果可以反映阀门内部流动的变化规律,为降压阀的合理设计提供理论依据和参考。
