Iridium/ORBCOMM 机会信号融合定位技术

秦红磊 李志强 赵超

(北京航空航天大学 电子信息工程学院, 北京 100083)

开展机会信号[1](signal of opportunity,SOP)定位技术的研究为解决全球导航卫星系统(global navigation satellite system,GNSS)不可用情况下的导航定位问题提供了有效途径。 机会信号包括陆基机会信号和天基机会信号,如DTV、WIFI 及移动通信网络信号等为陆基机会信号,低地球轨道(low Earth orbit,LEO)星座信号为天基机会信号。本文主要研究LEO 星座机会信号定位技术。LEO 星座机会信号用于定位具有许多优点,如全球覆盖、可利用频带宽、抗电磁干扰能力强、不需要系统建设、成本低等。 LEO 星座多以全球无缝、终端可手持的大容量移动卫星通信系统为主,目前运营良好的有Iridium、ORBCOMM 和Global-Star 等。 另外,OneWeb 公司计划构建含有648 颗卫星的LEO 星座[2],SpaceX 公司也在计划一个含有4 000颗卫星的LEO 星座[2],为未来LEO 星座机会信号定位提供了丰富的辐射源。

单LEO 星座构型和可见星数量往往不能同时满足高精度、高可用性的定位要求,如ORBCOMM 星座布局较好,但目前在轨运行可工作的卫星数目只有12 颗, Iridium 系统在轨运行66 颗工作卫星,但Iridium 轨道全为极地南北走向轨道,星座布局不利于高精度定位。 Iridium 和ORBCOMM 星座互补性高,二者融合定位可解决单LEO 星座定位精度差的问题。

基于LEO 天基机会信号的研究刚刚起步。国内学者发表了Iridium、ORBCOMM 单LEO 星座机会信号定位技术[2-5],前者定位精度优于200 m,后者定位精度优于140 m,并进行了误差分析;另外还进行了Iridium 辅助惯性导航系统(inertial navigation system,INS)动态定位研究[6]。 国外研究主要集中在美国加利福尼亚大学和加拿大魁北克大学,加拿大学者Nguyen 等[7-8]研究了Iridium定位技术;美国学者Kassas 和Khalife[9]研究了ORBCOMM 定位技术,精度达到360 m,并进行了辅助INS 实验[10];在多LEO 星座机会信号融合定位技术方面,目前只有加拿大学者Farhangian和Landry[11]使用扩展卡尔曼滤波(extended Kalman filter, EKF)的方法对Iridium 和ORBCOMM融合定位进行了研究,精度达132 m。

本文基于Iridium 和ORBCOMM 星座开展了多LEO 星座机会信号融合定位技术研究。 首先,分析了瞬时多普勒定位原理;然后,构建了Iridium/ORBCOMM 机会信号融合定位模型,包括信号接收机模型、直接融合定位模型和Helmert 融合定位模型;最后,利用实际信号进行了实验验证,获得了优于70 m 的定位精度。

1 瞬时多普勒定位原理

LEO 星座机会信号定位技术采用瞬时多普勒定位原理,本节主要从几何角度详细分析多普勒定位原理,为后续Iridium/ORBCOMM 机会信号融合定位奠定基础。

1.1 等多普勒频率圆锥面

由多普勒理论可知,卫星信号被相对于地球静止的接收机接收时,信号载波产生的多普勒频率如下:

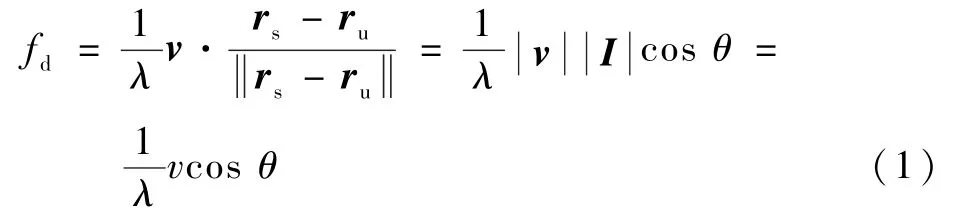
式中:fd为多普勒频率;λ为信号波长;v为卫星在地心地固坐标系(Earth centered Earth fixed,ECEF)下的速度矢量;I为卫星与接收机视距方向单位矢量;rs∈R3为卫星在ECEF 下的位置矢量;ru∈R3为接收机在ECEF 下的位置矢量;θ为卫星速度矢量与视距方向矢量的夹角;v为速度矢量的模。

假设地球表面放置接收机R,测量空间LEO卫星S辐射信号的多普勒频率。 在三维空间内不考虑任何误差的情况下,根据式(1)可知,与接收机测量的多普勒频率相等的位置矢量构成一圆锥面,顶点为卫星位置矢量,圆锥面张角为θ,该圆锥面即为等多普勒频率圆锥面。 理想情况下,圆锥母线无限长,如图1 所示,图中仅取部分等多普勒圆锥面。

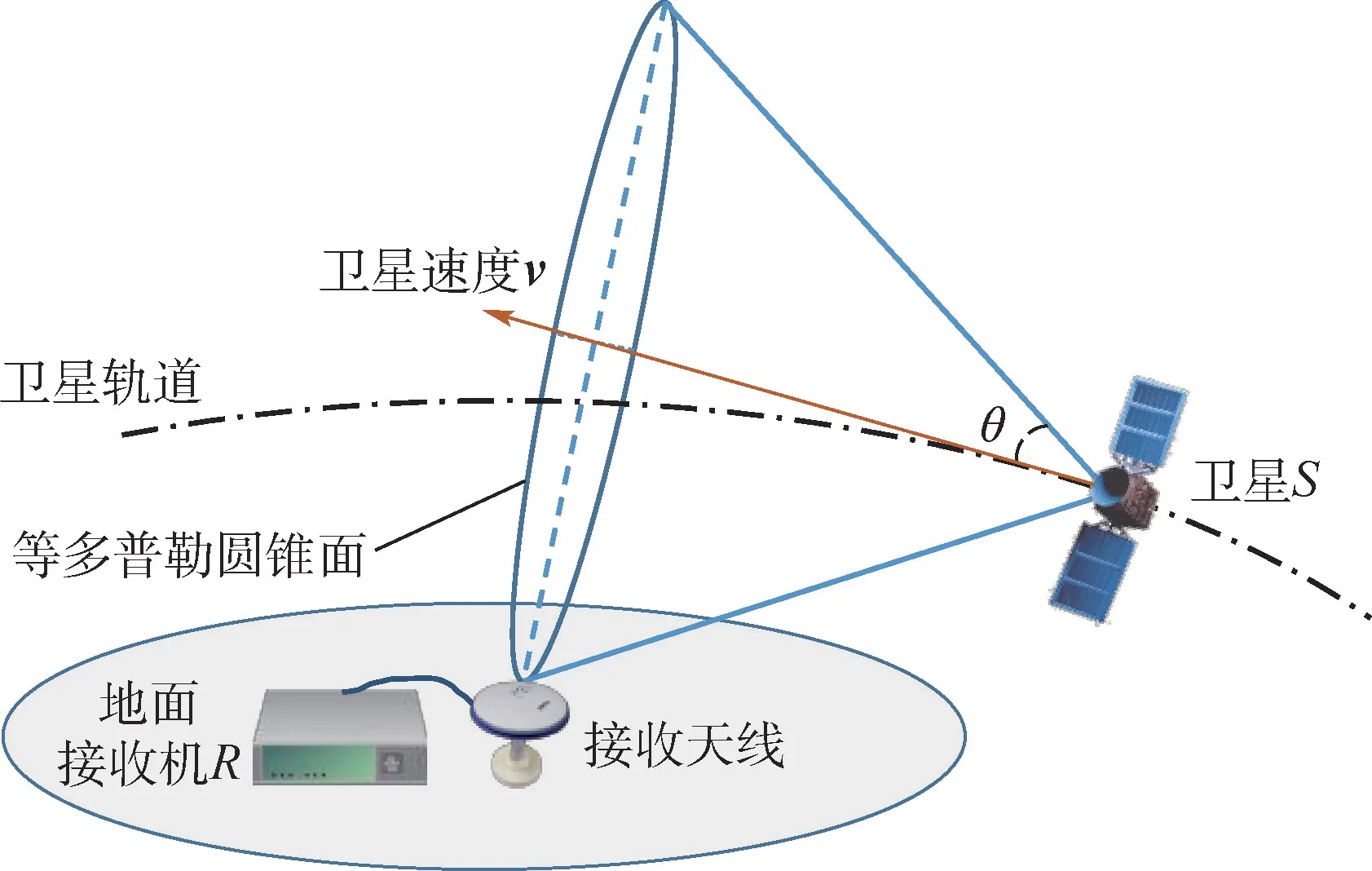
图1 等多普勒频率圆锥面示意图Fig.1 Diagram of a conical surface composed of points with equal Doppler frequencies

1.2 多普勒频率测量误差对等多普勒频率圆锥面的影响

考虑只有多普勒频率测量误差存在,当产生的多普勒频率测量误差为Δf时,此时的等多普勒频率圆锥面的张角变为

猕猴桃作为新兴水果，市场售价比普通水果更高，而且也是速生丰产的树种，常规管理可达一年栽植、两年见果、三年投产、四年丰产，故可获得较高的经济价值。

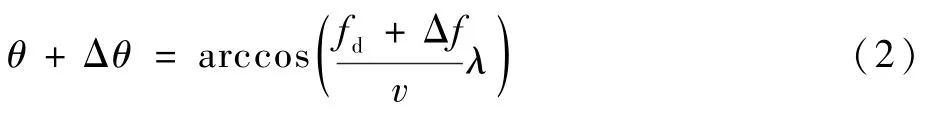
式中:Δθ为由多普勒频率测量误差Δf引起的等多普勒频率圆锥面的张角增量,如图2 所示。 假设用户真实位置为图2 中A点,在A点测量的无误差多普勒频率为fd,测量误差导致多普勒频率为fd+Δf,使得接收机位置矢量从A偏到B′,定位时,求解的定位结果就位于虚线圆锥面上。 因此,测量误差导致等多普勒频率圆锥面变成了侧面带有一定厚度的圆锥面,以下简称圆锥环体。该圆锥环体在地面可形成一簇等多普勒频率曲线,如图2(b)所示,该区域为接收机可能存在的位置。

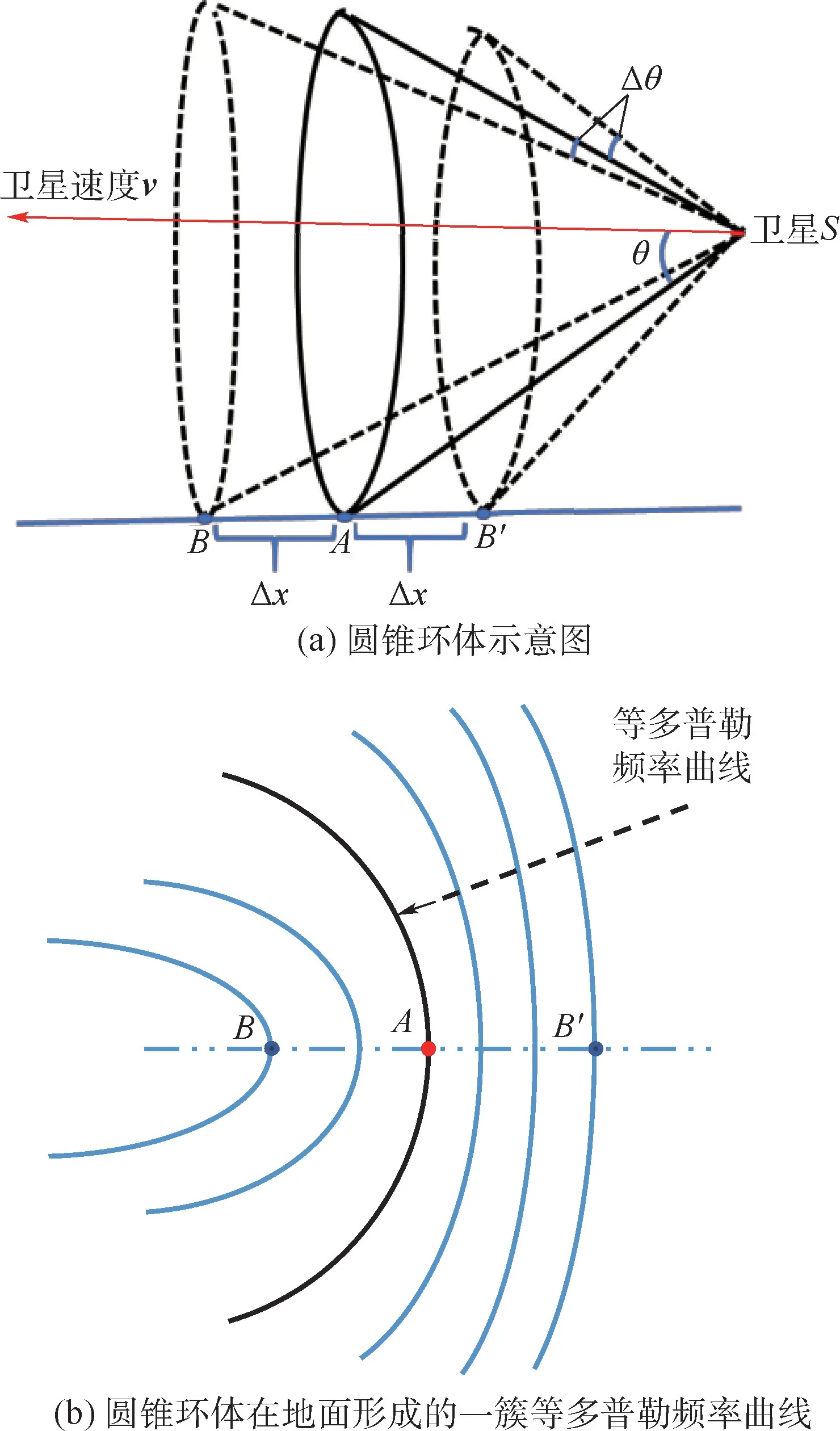
图2 多普勒频率测量误差对图1 中圆锥面的影响Fig.2 Influence of Doppler frequency measurement error on conical surface in Fig.1

1.3 圆锥面张角增量对圆锥环体体积的影响

瞬时多普勒定位的几何解释是利用至少4 个多普勒频率圆锥面相交确定用户位置和钟偏。 事实上,由于多普勒频率测量误差存在,由1.2 节可知等多普勒频率圆锥面变成了圆锥环体,用户位置估计值将不再是空间一点,而是分布在几个圆锥环体的交叉体内,该交叉体体积越大,位置估计误差越大。 由推导可知,多普勒频率测量误差Δf导致等多普勒频率圆锥面的张角θ发生改变,多普勒频率引起视距速度的模vlos发生改变:

显然,当卫星速度矢量与视距方向矢量的夹角θ不同时,由相同的测量误差Δf引起的张角增量是不同的,当卫星处于接收机头顶位置时,θ越接近π/2,因此sinθ越大,由多普勒频率测量误差引起的张角增量最小。 张角增量越小,圆锥环体的厚度就越小,最终的交叉体体积也就越小,定位误差就越小。 可得出,在利用瞬时多普勒定位模型解算时,需要考虑多普勒频率圆锥面张角θ对测量误差的放大作用。

2 Iridium/ORBCOMM 机会信号融合定位模型

2.1 信号接收机模型

信号接收机模型要依据信号体制进行设计,Iridium 和ORBCOMM 星座构型与信号体制如图3所示。

图3 Iridium 和ORBCOMM 信号体制Fig.3 Iridium and ORBCOMM signal system

Iridium 星座[12-13]在轨运行75 颗卫星,包括66 颗工作卫星和9 颗在轨备份卫星,分布在6 个近极圆轨道,轨道倾角为86.4°,每个轨道共11 颗工作卫星,可实现包括南北两极的全球覆盖。Iridium频带为1 616. 0 ～1 626. 5 MHz,采用FDMA/TDMA /SDMA 多址接入,并采用TDD 实现双工。 1 626.0 ～1 626.5 MHz 为单工下行信道,分为12 个信道,每个信道频宽为41.667 kHz。 Iridium信号严格按照TDMA 帧结构发送信号,帧结构中的前20.32 ms 为单工信道使用,包括单音信号、BPSK 调制信号及QPSK 信号。

ORBCOMM 星座[13-15]在轨运行35 颗卫星,仍能工作的为第二代卫星(OG2),共12 颗卫星,均匀分布在4 个主轨道平面,轨道倾角为47°。 ORBCOMM 下行链路频带为137 ～138 MHz,有13 个FDMA 信道,其中12 个信道带宽为25 kHz,另外1 个带宽为50 kHz 的信道用于与关口站通信,信号采用对称差分相移键控(symmetrical differential phase shift keying,SDPSK)调制方式。 ORBCOMM上行链路频带为148 ～150 MHz,共6 个带宽10 kHz的FDMA 信道,与本文无关不再叙述。

通过对比不难看出,Iridium 星座在卫星数量方面明显优于ORBCOMM 星座,导致Iridium 可见性整体上优于ORBCOMM。 但是,Iridium 为近极圆轨道,卫星可见性会随着维度的下降而降低,在中低纬度地区定位效果会差很多。 另外,ORBCOMM 轨道倾角更小,卫星轨道走向非正南正北走向,可补充Iridium 轨道不足。 因此,两星座若融合定位,不仅可以增加卫星可见性,更可以优化星座构型,进一步提高定位精度并增强定位系统可靠性。

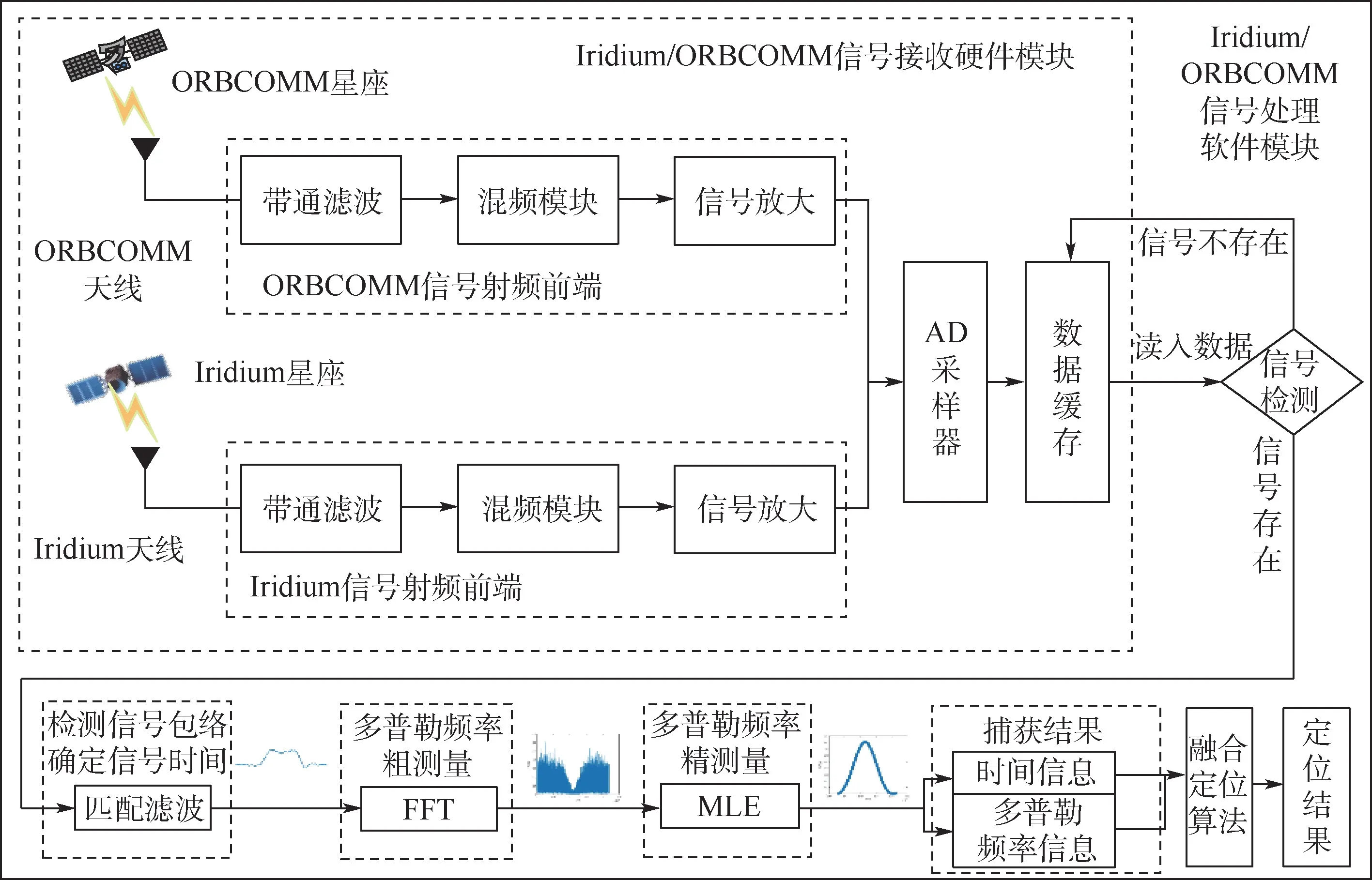
图4 Iridium/ORBCOMM 信号接收机模型Fig.4 Iridium/ORBCOMM signal receiver model

2.2 直接融合定位模型

静态接收机的瞬时多普勒观测方程为

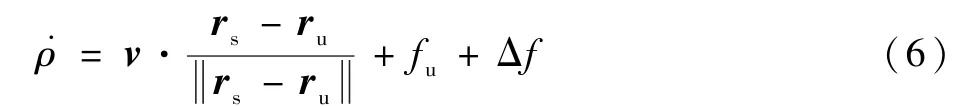
式中:̇ρ为观测伪距率, m/s;fu为接收机钟偏量;Δf为多普勒频率测量误差。

要实现Iridium/ORBCOMM 机会信号融合定位,由于接收机与各星座的钟偏不同,融合定位方程的状态量u将变成5 维向量,即

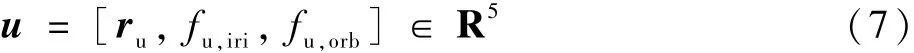
式中:fu,iri和fu,orb分 别 为Iridium 和ORBCOMM 的钟偏。

记Iridium 星座n维和ORBCOMM 星座m维多普勒频率观测量̇ρiri、̇ρorb为

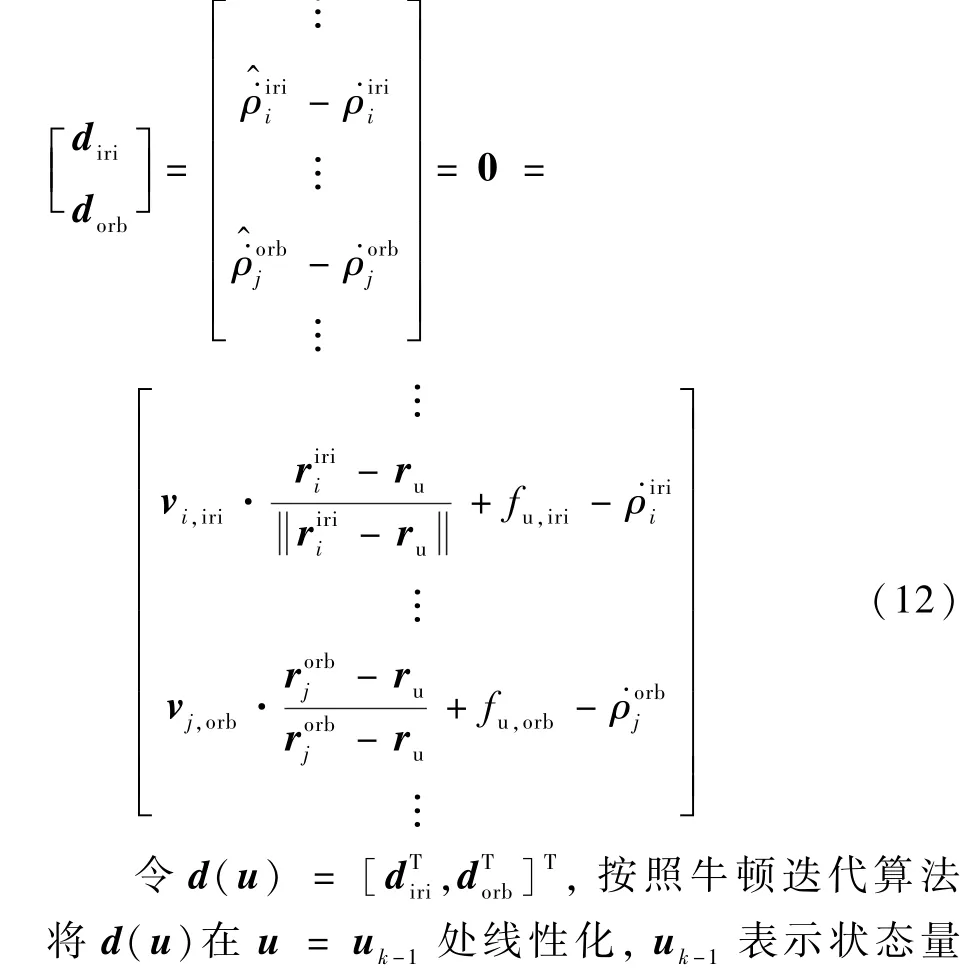
求得G如式(16),代入式(14)即为Iridium/ORBCOMM 机会信号直接融合定位模型。 式(14)亦可推广到N个LEO 星座机会信号融合定位,此时状态量u∈RN+3。

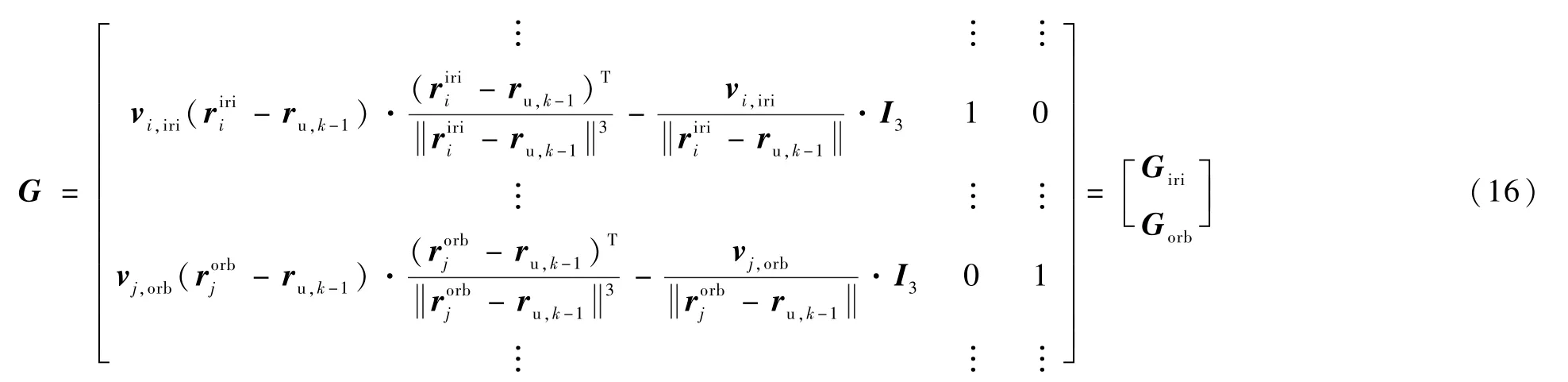
2.3 Helmert 融合定位模型

直接融合定位模型仅仅考虑Iridium/ORBCOMM 不同星座在定位中的钟偏问题,并未处理增加星座引入的测量噪声问题。 不同星座的信号体制、星座构型等多方面的原因导致不同星座卫星信号的观测值精确度不同。 为了减小测量噪声较大的星座对定位的消极影响,可采用加权最小二乘算法,即在式(14)等号两边同时乘以权值矩阵Q,可得

加权最小二乘算法的权值可根据后验信息确定。 后验信息指通过迭代计算获得的信息,主要指残差向量,可估计各星座观测量的方差,从而在迭代计算中动态地调整不同类型观测量的权值,实现较优的权值配置。 本文引入基于残差向量b的Helmert 方差估计[17-18],即通过残差向量估计不同星座的测量噪声方差,并将方差考虑进入权值矩阵,从而获得较优权值配置,进而降低不同星座测量噪声分布不同对定位结果的消极影响。 采用基于残差向量b的Helmert 方差估计定权的加权最小二乘算法记为Helmert 融合定位模型,基本流程如下:

步骤1 初始化权值矩阵和接收机位置,权值矩阵可设置为单位矩阵I,即W=I·I=I,根据大量试验结果,接收机初始位置可设置为以接收机为中心方圆1 000 km 之内的任意位置。

步骤2 将权值矩阵代入式(18),根据最小二乘迭代获得残差向量b=GΔ^u-d。

步骤3 根据参考文献[17]中Helmert 方差估计简化公式可得出式(19),为本文Helmert 方差估计函数,估计出各星座观测量误差的方差。

步骤4 将步骤3 中得到的方差按照式(20)更新权值矩阵,其中c为常数,一般可设置为1 ～2。

结合2.2 节,本文提出Iridium/ORBCOMM 机会信号融合定位算法,如图5 所示。 首先,通过信号接收及处理系统,获得多普勒频率及对应的时间信息;其次,考虑瞬时多普勒定位原理,尽量选取高仰角处的历元;再次,时间信息送入卫星轨道预测模块,结合TLE 文件和SGP4 轨道预测模型获得卫星位置及速度;然后,将多普勒频率和对应的卫星位置、速度送入直接融合定位方程进行迭代定位解算,获得直接融合定位结果;最后,考虑不同星座多普勒频率观测量精度不同,引入基于Helmert 方差估计的加权最小二乘算法,将方差估计值用于更新权值矩阵,迭代定位解算,直至定位稳定输出,获得Helmert 融合定位结果。 若接收机位置矢量高度分量为先验信息,可使用高程辅助[19]进一步提高定位精度。

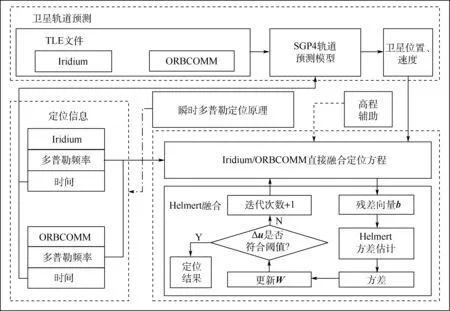
图5 Iridium/ORBCOMM 机会信号融合定位算法Fig.5 Iridium/ORBCOMM fusion positioning algorithm

3 实验验证

首先,介绍Iridium/ORBCOMM 机会信号接收及处理系统,并获得用于定位的多普勒频率及时间信息;然后,验证Iridium/ORBCOMM 机会信号融合定位算法,获得融合定位结果,并对结果进行分析。

3.1 Iridium/ORBCOMM 机会信号接收及处理

图6 为Iridium/ORBCOMM 机会信号接收及处理系统,主要包括天线、射频前端、AD 采样器及信号处理软件平台4 个部分。

图6 Iridium/ORBCOMM 信号接收系统Fig.6 Iridium/ORBCOMM real signal receiving system

持续接收Iridium 和ORBCOMM 机会信号1 h 11 min,期间接收机保持静止,测量卫星多普勒频率。 将获取数据分为连续的多个90 ms 数据块,当存在机会信号时,利用匹配滤波确定信号存在时间,使用FFT 粗测量多普勒频率,并采用MLE 算法精测量多普勒频率。 多普勒频率测量结果如图7 所示,这段时间内共捕获Iridium 卫星13 颗,ORBCOMM 卫星4 颗。

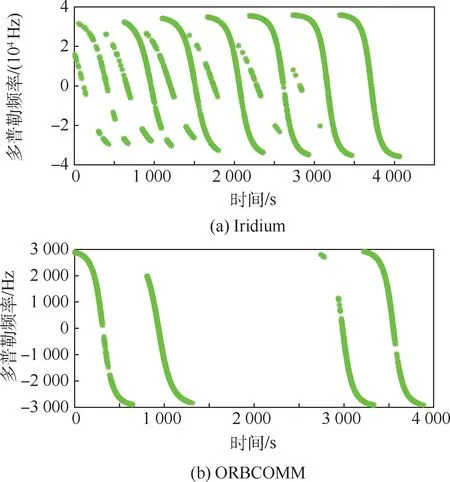
图7 多普勒频率捕获结果Fig.7 Capture results of Doppler frequency

3.2 Iridium/ORBCOMM 机会信号融合定位及结果分析

按照本文提出的Iridium/ORBCOMM 机会信号融合定位算法实现接收机静态定位,分为Iridium 机会信号定位、ORBCOMM 机会信号定位、Iridium/ORBCOMM 机会信号直接融合定位及Iridium/ORBCOMM 机会信号Helmert 融合定位4 种情况。 将所有捕获得到的不同时刻的多普勒频率测量值均匀分组,每组中随机选取一个测量值,在高程辅助的情况下进行500 次定位解算,以高精度GNSS 定位结果为参考值,每50 次定位为一组,统计定位误差均值和均方根误差(root mean square error, RMSE)值。 图8 ～图11 分别给出了上述4 种情况下定位误差的统计结果。

图8 给出了Iridium 单星座机会信号定位误差统计结果,水平方向定位误差均值和RMSE 均优于150 m;图9 给出了ORBCOMM 单星座机会信号定位误差统计结果,水平方向定位误差均值和RMSE 值均优于125 m;图10 给出了Iridium/ORBCOMM 机会信号直接融合定位结果,双星座优化了卫星空间分布,其水平方向定位误差得到改善,水平方向定位误差均值和RMSE 均优于85 m;图11 给出了Iridium/ORBCOMM 机会信号Helmert 融合定位结果,引入Helmert 方差估计将双星座间的观测量测量精度不同对定位结果造成的消极影响削弱,其水平方向定位误差得到改善,水平方向定位误差均值和RMSE 均优于70 m,尤其东向和北向的定位误差均值在30 m 左右。4 种定位方式水平方向定位误差均值和RMSE 值如表1所示(均取最大值)。 不难看出,多星座融合定位可以进一步提高定位精度。

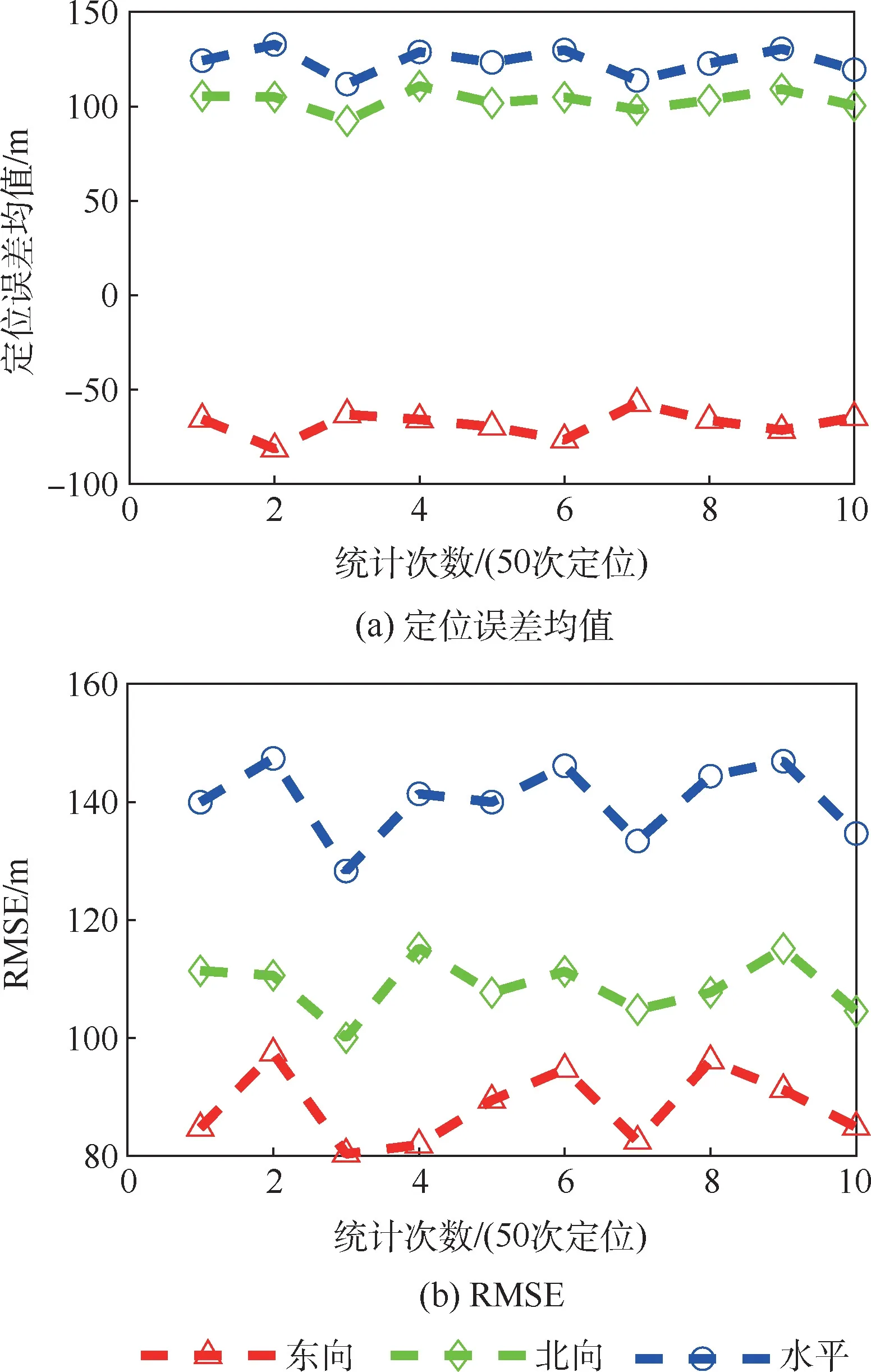
图8 Iridium 机会信号定位结果Fig.8 Positioning results of Iridium signal of opportunity

图9 ORBCOMM 机会信号定位结果Fig.9 Positioning results of ORBCOMM signal of opportunity

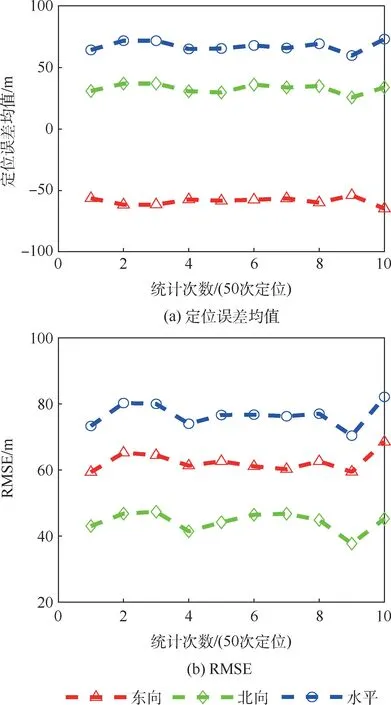
图10 Iridium/ORBCOMM 直接融合定位结果Fig.10 Iridium/ORBCOMM fusion positioning results

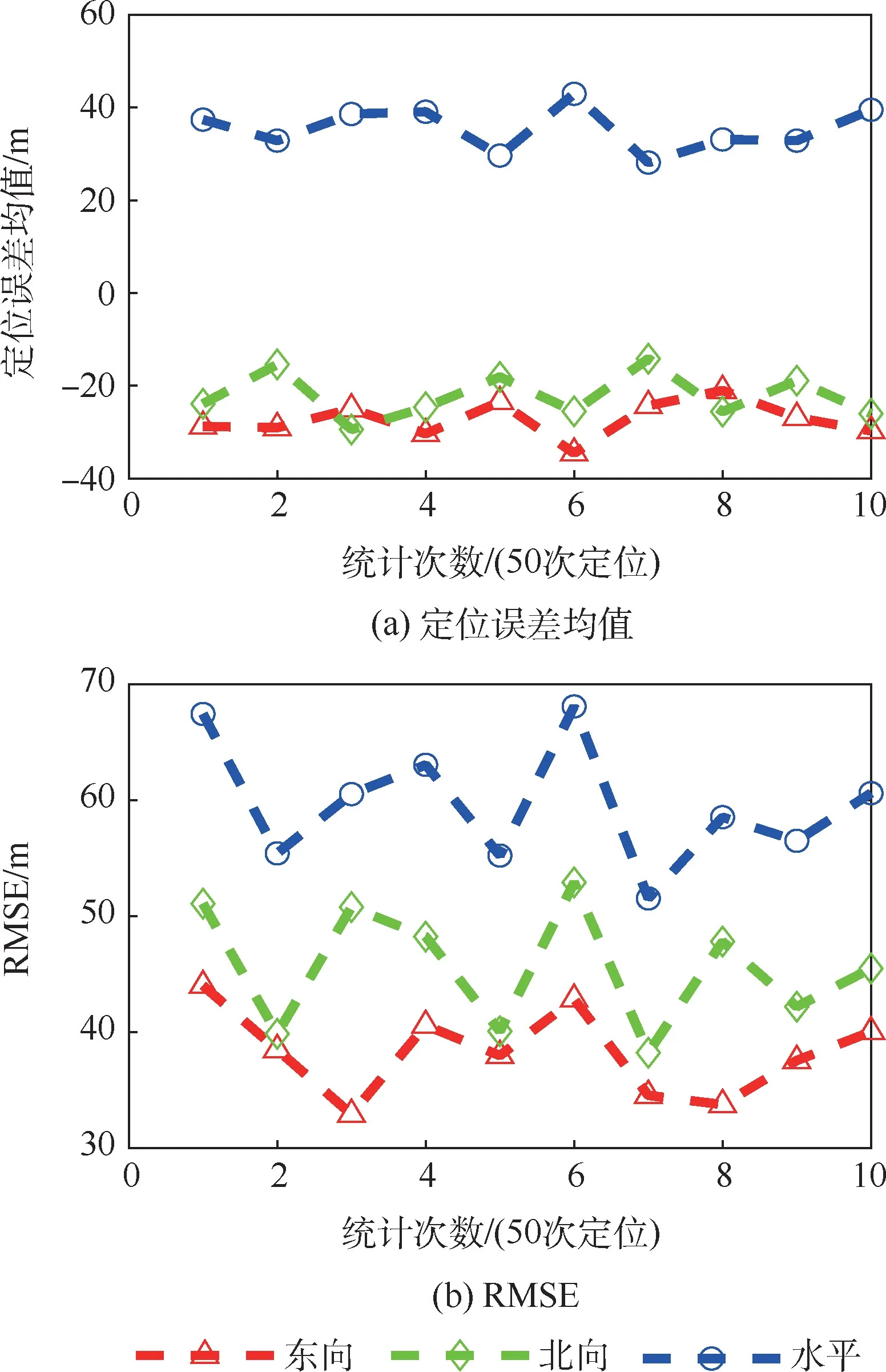
图11 Iridium/ORBCOMM Helmert 融合定位结果Fig.11 Iridium/ORBCOMM Helmert positioning results

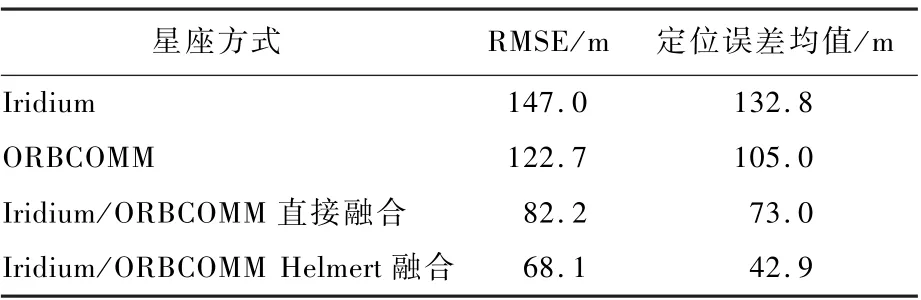
表1 高程辅助情况下不同方式定位结果对比Table 1 Comparison of positioning results of different methods with altitude aiding

4 结 论

本文针对单星座机会信号定位存在几何结构差的问题,提出了多星座融合加权定位方法,提高了LEO 机会信号可视性。 同时,建立了Iridium/ORBCOMM 机会信号融合定位模型,并提出了基于Helmert 方差估计的Iridium/ORBCOMM 机会信号融合定位算法,实验验证在高程辅助情况下水平方向定位精度优于70 m,比当前研究水平精度提高了近一倍。 研究成果为GNSS 不能正常工作的场景提供一种有效的定位手段,所采用的融合方法显著提高了LEO 卫星机会信号定位的精度和可用性。

观测多普勒频率存在野值点,影响定位结果,需考虑采用抗差最小二乘算法实现对野值点的剔除,进一步提高定位精度。