旋压钻进破岩的应力特征研究

2022-11-08徐振洋吴怡璇王雪松郭连军柴青平

金属矿山 2022年10期

徐振洋吴怡璇王雪松刘鑫郭连军柴青平

(1.辽宁科技大学矿业工程学院,辽宁鞍山 114051;2.辽宁省金属矿产资源绿色开采工程研究中心,辽宁鞍山 114051;3.沈阳工业大学建筑与土木工程学院,辽宁沈阳 110870;4.鞍钢集团矿业有限公司,辽宁鞍山 114001)

岩石破碎机理是采矿工程、岩土力学研究的重要方向,在钻探过程中,钻头的形状对岩石破碎时受力情况有很大影响,常见压头形状有球形、圆柱形、锥形等,钻头与岩石接触时的应力分布是不均匀的[1],上世纪70年代,Pang S S 等[2]对锥形、楔形和半球形压头在载荷作用下的响应特征进行研究,为不同类型钻头破岩效率和裂纹扩展规律提出新的研究方向。Munoz H 等[3]通过室内切削岩石试验,利用2个基本的钻井参数比能和钻速来分析岩石的性质,研究冲击作用下钻速与纯切削能耗的关系。曹瑞琅等[4]利用室内数字钻进试验设备,提出一种钻进过程指数评价岩体的完整性。Chang Heon Song 等[5]为了更精准地获取钻进数据,建立了一套新的钻进效率测试系统,对岩石进行了现场和实验室钻进试验,以获得岩石性质的初步定量评价。冯上鑫等[6]利用自制的旋切测试仪器研究了钻头在不同角度下扭矩与加载力之间的关系。室内钻进试验对岩石的强度和钻机参数关联性有了初步探究,但是钻头破坏岩石的过程是微小且无法肉眼监测破碎过程,针对钻头与岩石交互时的应力分布理论研究尚不完善,细观参数难以从物理实验获取[7],达不到快速获取岩石破碎时应力的目的,因此仿真模拟是进行岩石力学方面研究的重要手段。

目前计算机仿真对于岩石动力学的研究进入成熟阶段,对于研究切削齿的形状、材料、尺寸等对破岩体积和破岩应力方面得以较好研究。郭汝坤等[8-9]利用CDEM 模拟单齿破岩过程并估算破岩体积。陈晓君等[10]对4种岩石进行相同钻进条件下的模拟研究,分析岩石的固有频率进而识别岩性。在PDC 钻头破岩研究中,邹德永等[11]研究得到斧形PDC 齿的破岩效率高,验证其较传统PDC 齿形提高55%的效率。Zhang C L 等[12]在理论与试验的基础上建立PDC 钻头破岩模型,定量分析了刀具的切削量、载荷分布、移动速度等。江红祥等[13]利用模拟手段研究了半球形机械齿冲击破岩的细观变化规律,与物理实验的平均误差在15%以下。

上述学者通过仿真手段对破岩效率进行论述,以及单齿切削岩石的体积问题进行研究,解决了现场试验受限问题。然而,现有研究集中于钻头静态破岩的宏观力学特性,对于平底圆柱刚性钻头旋压破岩规律研究尚不充分。本研究利用ABAQUS 有限元软件,对平底圆柱刚性钻头的破岩规律进行模拟,分析钻头作用在岩石上的径向和轴向应力变化规律,以及转速和钻压对应力变化的影响,进而对室内研磨、可钻性等试验参数选定提供参考。

1 钻进破岩模型

平底刚性钻头旋压钻进岩石的破岩规律不同于静态压入岩石试验,旋压钻进是在静压与剪切破坏共同作用下破岩,在研究岩石的可钻性和耐磨性方面采用旋压钻进的方式,钻头受到压强和扭矩的作用下,底面接触岩石的应力分布并不均匀,为此探究钻头破碎砂岩时的应力分布规律,以便于在试验和现场应用中更合理地选取钻进参数。

1.1 有限元模型建立

利用有限元仿真软件ABAQUS 建立单齿刚性钻头破岩模型,如图1所示,钻孔直径15 mm,取有效钻深20 mm,钻杆直径6 mm,岩石尺寸为标准圆柱形试件ϕ50 mm×100 mm,钻头与岩石水平表面夹角为90°[14],金刚石钻头设置为刚性材料,岩石内部网格采用C3D8R 正六面体单元类型,中间接触单元加密。

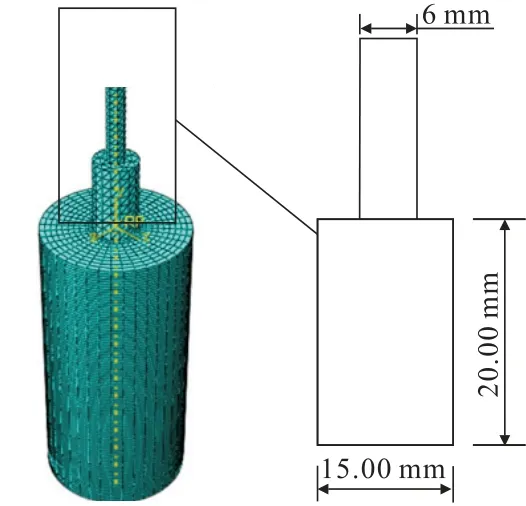
图1 钻头与岩石数值模型Fig.1 Numerical model of drill bit and rock

1.2 材料模型参数

钻头加载方式为恒转速和钻压,为研究钻压和转速对不同种类岩石钻进速度的影响,对砂岩试件进行钻进模拟,根据王玉杰等[14]进行的数字钻进系统设定参数,模拟选定钻压范围为2～4 kN,转速选定为400、800、1 200 r/min,钻头设为刚体,模拟时间为钻头钻进岩石20 mm时停止作业。

1.3 岩石屈服准则及基本假设

刚性头和岩石采用表面与表面接触模式,岩石材料设置为Drucker-Prager 准则[15],破坏形式为剪切破坏,超过破坏位移时网格删除,岩石材料属性如表1所示。

表1 岩石材料属性Table 1 Rock material properties

对模型提出假设:① 岩石内部为均质岩石,无裂隙、损伤等破坏;② 不考虑温度、岩屑对钻头钻进的影响;③ 岩石四周和底面铰固,不会发生摩擦位移;④ 钻头的变形和磨损对实验的影响忽略不计。

2 钻进破岩规律

2.1 破岩过程分析

平底圆柱刚性钻头在钻进岩石时,岩石受到钻机液压缸施加的静荷载,同时受到钻头旋转以及接触冲击的动荷载,在冲击、剪切的共同作用下破碎岩石,钻进过程中材料会发生弹性变形、塑性变形、剪切破坏及冲击破坏,由于岩石是脆性材料,塑性变形可忽略不计[16]。分别对不同钻压和转速的刚性标准钻头钻进岩石过程进行模拟,岩石发生破坏时的相对位移和应力如图2所示。

图2 进尺位移的应力分布Fig.2 Stress distribution of feeder displacement

钻头接触岩石时,扭矩和钻压共同作用下,钻头外圈接触的岩石最先发生破坏,表面中心点在外圈发生破坏后出现应力集中现象,随之稳定钻进岩石。图2 显示钻进位移为0.018 5 mm时,钻头接触径向半径3 mm处出现应力集中现象,应力达到79.68 MPa,岩石表面出现破碎点;钻进深度为0.035 7 mm时岩石边缘单元失效;当钻进深度达到0.060 3 mm时,岩石与钻头接触中心部位出现应力集中现象,应力达到89.56 MPa。由于岩石是一种脆性材料,钻头接触应力达到岩石的抗压强度即为破碎[16],0.060 3 mm是岩石中心破坏的临界深度。

2.2 岩石破坏应力分布

为了研究转速和钻压对岩石破坏的影响,对岩石中心位置、边缘位置上的点应力,以及岩石径向和轴向应力分布进行分析,中心位置和边缘位置参考点以及岩石径向和轴向分析路径如图3所示。

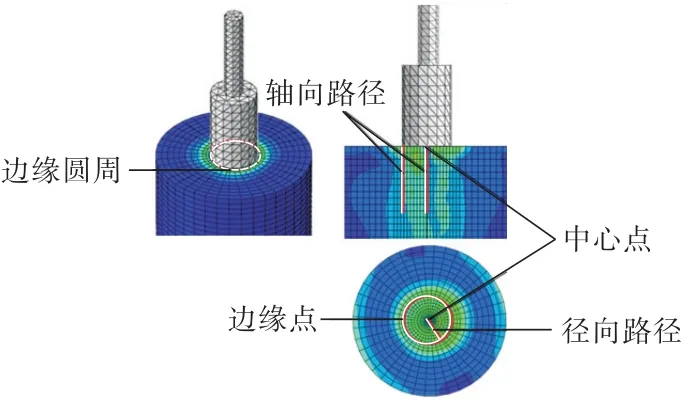
图3 应力参考点及路径的选择Fig.3 Selection of stress reference points and paths

2.2.1 岩石表面结点应力

表面岩石破坏过程如图4所示,可以看出4.05 s岩石接触外圈表面单元开始失效,岩石与选头接触表面由外向内发生破坏,中心位置最后发生破坏,因此选取岩石表面与钻头接触的中心位置和最外圈单元上点的应力进行研究,2 kN 钻压和425 r/min 转速钻进砂岩试件时,钻头位移和接触监测点的应力时程曲线如图5所示。

图4 岩石表面单元破坏过程Fig.4 Failure process of rock surface units

图5 应力时程曲线及钻头位移曲线Fig.5 Stress time curves and drill bit displacement curve

钻头稳定钻进前期,边缘点应力大于中心点的应力,中心点峰值应力为74.02 MPa、边缘点为66.22 MPa,边缘点出现应力峰值早于中心点2 s。边缘峰值应力小于中心点的峰值应力,可以说明钻头旋转过程中岩石的剪切破坏跟接触的径向半径有关,且随着径向半径的增大,岩石受到的剪切力越大,发生破坏的应力峰值越小,所以岩石表面单元边缘点先发生失效。边缘点应力曲线出现多个峰值,是由于钻头与岩石接触面积较大,从位移曲线上可以看出钻头不断上下波动,钻进前期会产生较大的反作用力于钻头上,导致钻头发生纵向振动效应,以对岩石造成冲击破坏作用。

2.2.2 轴向应力分布规律

2 kN 钻压和425 r/min 转速钻进砂岩试件的轴向应力分布如图6所示。中心轴向路径上的节点应力分布如图6(a),中心轴向路径上应力分布随深度的增加整体呈先上升后下降的趋势,临近破坏时轴向应力最大值达到32.76 MPa,此时深度为5.99 mm,在5.99～7.99 mm之间,应力出现聚集现象,同一深度的节点应力在破坏前随时间的增加而增加,破坏后岩石各节点应力波动较大,总体呈下降趋势。

图6 中心点与边缘点的轴向应力分布Fig.6 Axial stress distribution at the center position and edge position

边缘点比中心点受力较大且破坏先于中心点的原因,破坏前边缘轴向路径节点应力随深度的增加而降低,与中线轴线破坏前应力变化规律相同,如图6(b),4 s 时轴向深度4.78～7.99 mm之间出现波动,在5.99 mm时出现应力聚集现象,最大应力为38.57 MPa;在16 mm深处出现应力集中,最大应力为14.73 MPa,表面岩石应力传递的范围即是应力集中位置,16 mm之后应力随深度逐渐下降,钻头有效研究的轴向应力作用范围在16 mm范围内,16 mm之后的岩石受到的应力达不到内部裂纹扩展以及发生变形的最大应力。

2.2.3 径向应力分布规律

钻头旋转过程中接触岩石的圆周径向节点受转矩作用与岩石发生剪切破坏,转矩跟矩心的位置成正比关系,具体的计算式如下[17]。

式中,M为转矩,N·m;F为矢量力,N;ρ为径向半径,即钻头与岩石接触圆形表面的半径,m;τ为剪应力,MPa;Ip为极惯性矩,纯几何量,无量纲;d为旋转截面直径,m。

选取岩石表面同一时刻3条路径上的应力分布对比,如图7所示,分别为发生破坏时、未发生破坏时、临近破坏时的3条径向路径。在破坏时和临界破坏时应力随半径的增大呈先增大后减小的趋势,说明岩石边缘的单元比中心单元更容易失效。峰值应力在距圆心3 mm处,最大应力达到73.74 MPa,未发生破坏时的应力随半径的增大而增大,靠近钻头半径时的应力基本一致,稳定在37.06～43.97 MPa。岩石径向剪切应力随径向半径的增大而增加,岩石截面剪切力是矢量与主应力的方向相反,存在剪应力和正应力共同作用最大应力位置,是决定岩石发生破坏的优先切入点。

图7 岩石表面径向应力分布Fig.7 Radial stress distribution on rock surface

2.3 钻压对破岩应力的影响

钻压是影响钻进速度重要的指标之一,分别对砂岩在2、2.25、2.5、3、4 kN 时钻进速度进行分析,平均速度如表2所示。

表2 不同钻压下的平均速度Table 2 Average velocities at different bit weights

钻进速度根据钻压的增长无明显增长规律,在2 kN 和425 r/min 转速时,钻头以3.02 mm/s 的速度进尺,当增加钻压到2.5 kN 时,钻头没有钻进岩石,因此针对2.25 kN 和2.5 kN 进一步分析。钻进砂岩的过程中,2.25 kN 和2.5 kN 的钻压在转速为425 r/min 时(图8),10 s 的时间只造成岩石表面轻微破坏,从应力曲线上可以看出,中心点的应力没有较大波动,始终保持平稳的应力状态。

图8 应力分布与模拟对照Fig.8 Comparison of stress distribution and simulation

2.4 转速对破岩应力的影响

转速针对不同强度岩石时,会出现不同的破碎效果,在钻压为2 kN 时,分别对静压作用下以及转速为425、600、800、1 000、1 200 r/min 时的应力分布进行分析,应力时程曲线和位移曲线如图9所示。

图9 径向应力分布和应力—时程曲线Fig.9 Radial stress distribution and stress-time history curve

静压作用下,岩石径向半径的应力近似不变,同一钻压下,钻头钻进速度800 r/min＞425 r/min＞600 r/min＞1 000 r/min＞1 200 r/min,研究中发现,高转速低钻压并不能提高钻进速度,6种转速的岩石表面径向应力以及中心点应力如图9所示,静压时,岩石应力随径向半径的增加呈线性减小,转速为600 r/min和1 000 r/min 时,岩石径向应力曲线和中心点应力曲线近似重合,与其他转速的曲线差异较大,随着径向半径的增加,径向应力与静压破坏接近;425、800、1 200 r/min 转速时,岩石表面径向应力以中心点为中点呈对称分布,中心点的应力最低,径向半径在4 mm时出现峰值应力,达到51.31 MPa,约为抗压强度三分之二,整体应力是静压时应力的5 倍,是因为在旋压过程中,岩石同时受到剪应力和压应力,2种应力的叠加效应大于静压时岩石受到的应力,在4 mm处出现峰值,岩石表面的剪应力沿径向半径增大,并在轴向压应力的作用下出现最大应力集中部位,从径向看,在0.533 倍径向半径处岩石优先于其他位置岩石发生破坏。