钢箱-混凝土组合梁滑移有限元分析

2022-11-07张宇航宋秀豪毛一波陈子豪

特种结构 2022年5期

张宇航宋秀豪毛一波陈子豪

山东建筑大学交通工程学院济南250101

引言

钢箱-混凝土组合梁通过剪力连接件将钢箱梁与混凝土翼板连接起来并协同工作，充分发挥了两种材料的优点，减轻结构自重，提高材料利用率［1］，已在实际工程中得到广泛应用［2］。但是剪力连接件并不能使钢梁与混凝土翼板完全成为一个整体，组合梁在受弯破坏过程中将发生界面滑移［3］。

国内外学者对钢梁与混凝土翼板之间的滑移已展开大量的理论分析与试验研究。Bojan［4］等提出一种基于应变且考虑了非线性材料和接触模型的有限元公式，并引入了广义滑移的概念，将数值计算结果与试验结果进行对比，证明了该公式的计算效率和准确性；Girhammar 等［5］分析了具体情况下组合梁的振动特性，说明了滑移效应对其产生的影响，并通过试验和有限元计算验证了提出的理论。樊健生等［6］根据栓钉的刚度方程和滑移微分方程求解了连续组合梁负弯矩区的滑移及滑移应变，并根据典型荷载工况下的滑移应变解推导出组合梁在负弯矩作用下的弹性抗弯承载力计算公式；余志武等［7］利用Goodman弹性夹层假设，推导了钢-混凝土组合简支梁的界面滑移和挠度变形的理论计算公式，并通过有限元分析验证了试验结果的准确性；王文炜等［8］利用钢-混凝土组合梁单元建立了考虑滑移的钢-混凝土组合梁有限单元法，并通过对试验梁的分析计算验证了此有限单元法的正确性；邹杨等［9］推导了考虑截面滑移效应的简支组合梁在多种荷载工况下的弯曲应力和界面剪力的解析解，得到了弯曲应力和界面剪力在各种荷载工况下的变化规律。

但上述试验及理论计算方法仅对工字形钢-混凝土组合梁进行研究，对钢箱-混凝土组合梁中滑移效应产生的影响研究较少，只有班志鹏、郑艳等［10］推导了受负弯矩作用的部分填充式钢箱-混凝土组合梁的滑移微分方程及滑移效应影响下组合梁弹性抗弯承载力计算公式，并进行了加载试验以验证公式的准确性。

为研究在栓钉连接下钢箱梁与混凝土翼板之间产生的滑移分布规律，本文设计了四根剪力连接度不同的钢箱-混凝土组合梁进行数值模拟，分析各组合梁滑移情况与极限承载力的变化，探究界面滑移对组合梁力学性能产生的影响。

1 有限元分析

1.1 有限元模型建立

本文运用有限元软件ABAQUS 对钢箱-混凝土组合梁进行模拟分析，共设计四根组合梁，钢箱梁与混凝土之间采用栓钉连接，通过改变栓钉数量来控制组合梁的剪力连接度，四根组合梁的栓钉数量分别为140、112、84、56 个，剪力连接度依次为1.25、1.0、0.75、0.5。除剪力连接度不同外，其他构造参数均相同，组合梁全长4200mm，计算跨径为4000mm，梁总高360mm，钢箱梁高280mm，混凝土翼板厚80mm，为防止数值计算过程中梁体发生失稳破坏，在两腹板之间增加6道横隔板。按剪力连接度由大到小顺序将各组合梁分别编号为L1、L2、L3、L4，以L1 为例，钢箱-混凝土组合梁有限元几何模型如图1所示。

图1 L1 几何模型Fig.1 Geometric model of L1

组合梁构造及材料细节参数见表1，表1 中a为栓钉间距，hw为横隔板高度，tw为横隔板厚度，d为栓钉直径，L 为栓钉高度，fu为混凝土棱柱体轴心抗压强度。

表1 组合梁构造及材料细节参数（单位：mm）Tab.1 Construction and material detail parameters of the composite beam（unit：mm）

混凝土翼板采用八结点线性六面体减缩积分单元C3D8R模拟，基本尺寸取25mm；钢箱梁采用四节点曲面薄壳或厚壳减缩积分单元S4R 模拟，基本尺寸取25mm；内置钢筋采用两结点线性三维桁架单元T3D2 模拟，基本尺寸取30mm，节点平动自由度与混凝土自由度耦合。加载方式为双点跨中加载，结构平衡状态控制采用位移收敛准则。以L1 为例，组合梁网格划分有限元模型如图2 所示。

图2 L1 网格划分Fig.2 Grid division of L1

由于钢筋与混凝土之间视为无相对滑移，故将钢筋笼直接内置到混凝土之中；钢材与混凝土之间的接触面在切向采用罚函数，摩擦系数取0.2，法向采用硬接触；而钢箱梁与混凝土之间起连接作用的栓钉采用非线性弹簧单元SPRING2模拟，栓钉剪力-滑移关系式采用Ollgaard 等［11］提出的指数公式，剪力-滑移关系曲线见图3。

图3 栓钉剪力-滑移曲线Fig.3 Shear-slip curve of stud

式中：Qx、Qy、Qz分别为栓钉在横向、竖向及纵向所承受的剪力；δx、δy、δz分别为组合梁在横向、竖向及纵向的滑移量；Lst、Est、Ast分别为栓钉长度、弹性模量及横截面积；Qu为栓钉的极限抗剪承载力，按下式计算：

式中：Ec为混凝土弹性模量；fck为混凝土圆柱体标准抗压强度；fus为栓钉极限抗拉强度。

1.2 混凝土的本构关系

混凝土单轴受压应力-应变关系采用清华大学过镇海等［12］建议公式：

式中：y ＝σ／σ0，x ＝ε／ε0，σ0、ε0分别为应力峰值时应力、应变；αa、αd分别为曲线上升段、下降段参数。在本文分析中，取ε0＝0.002，αa＝2，αd＝2。本文取受压本构模型1／3σ0前为线弹性。

混凝土单轴受拉应力-应变模型采用上升段与下降段均为斜直线的线性软化模型，如图4 所示，曲线表达式如下：

图4 拉伸软化模型Fig.4 Tensile softening model

式中：σ、ε 分别为普通混凝土单轴受拉应力、应变；ft为普通混凝土单轴抗拉强度，εt0、εtu分别为混凝土拉伸峰值应变及拉伸极限应变，本文取εtu＝0.1。

1.3 钢材的本构关系

钢材本构关系采用双折线等向强化模型，钢材的屈服应力取为300.4MPa，而最大拉应力与屈服应力的比值在1.15 ～1.3 的范围内。最大载荷下的伸长率等于7.5%，弹性模量取为206GPa，泊松比为0.3，屈服后硬化斜率取初始弹性模量1／200。

2 计算结果分析

2.1 破坏形态

四根组合梁的破化模式类似，以L1 为例，组合梁的挠度云图如图5 所示。梁体略有弯曲，跨中发生向下位移，两端发生向上位移，跨中底板均达到屈服应变，腹板未发生屈曲变形，当荷载增至组合梁极限承载力时，跨中顶部混凝土达到压溃应变。

图5 L1 挠度云图（单位： mm）Fig.5 Deflection cloud diagram of L1（unit：mm）

2.2 受力特性分析

四根组合梁的荷载-挠度对比曲线如图6 所示，各组合梁受力过程相似，均经历了弹性阶段、弹塑性阶段及破坏阶段三个阶段，在开始加载至0.61Fu（Fu为组合梁的极限承载力）之前，各曲线均呈线性增加，组合梁处在弹性阶段，刚度保持不变，且完全抗剪连接的组合梁L1 与L2刚度基本相同，而部分抗剪连接的组合梁L3 与L4 的刚度比L1 小；随着荷载增至0.61Fu并继续增加，梁体进入弹塑性阶段，直至梁体破坏各曲线也未出现下降段，表明各组合梁延性良好；组合梁L2、L3、L4 的极限承载力与L1 相比分别减小3.97%、6.05%、11.16%，表明钢箱-混凝土组合梁的极限承载力会随剪力连接度的降低而减小。

图6 荷载-挠度对比曲线Fig.6 Load-deflection contrast curve

2.3 滑移分布规律

1.荷载-滑移量曲线

在组合梁的横隔板、跨中附近等位置等距布置7 个滑移测点（DH1 ～DH7），如图7 所示。

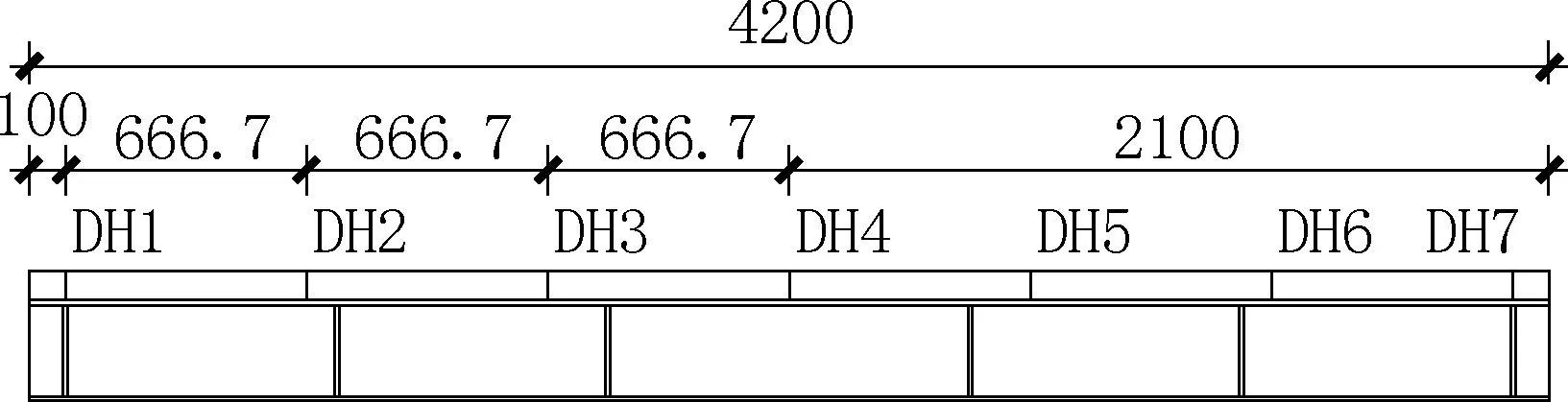
图7 滑移测点布置（单位： mm）Fig.7 Slip measurement point arrangement（unit：mm）

四根组合梁的滑移均呈现相同的发展规律，以组合梁L2与L4 为例说明，荷载-滑移量曲线如图8、图9所示。滑移呈明显的对称分布，从开始加载至梁体破环，跨中位置几乎无滑移发生，其他位置均发生不同程度的滑移。在弹性阶段，DH1至DH7处滑移均呈线性稳定增长，距跨中越远滑移量越大，视为滑移初始阶段；进入弹塑性阶段后，滑移增长速度减慢，随荷载继续增大，滑移开始减小，曲线呈现明显弯折，视为滑移发展阶段；最后梁体进入破坏阶段后，滑移开始迅速增大，DH3与DH5 处发展为滑移最大位置，视为滑移迅速增大阶段。对比图8、图9发现，剪力连接度越大，钢箱-混凝土组合梁的最终滑移量越小。