工业厂房吊车梁肩梁的疲劳失效机理分析及结构优化研究*

赵轩 徐浩然 陶修 陈春君 聂影 毛捷 王宇航

1.中冶赛迪工程技术股份有限公司 重庆400013

2.重庆大学土木工程学院 400045

引言

据大量研究及实际工程统计，钢构件的疲劳是导致钢结构断裂破坏的主要原因［1］，工程中金属疲劳是构件承受交变荷载反复作用的结果，该交变荷载往往低于构件的设计荷载，但在长期作用下，构件由于初始缺陷、恶劣环境等因素逐渐遭到损伤，最终表现为突发性的脆性开裂［2］。实际工程中的疲劳破坏受到许多不确定因素的影响，且疲劳强度与应力幅值、荷载作用频次及作用时间、连接及构造形式等几何物理参数均有关。

比起其他的建筑结构，钢结构工业厂房处在较为恶劣的工作环境中。在吊车往复运行过程中，钢吊车梁及其支座肩梁往往会在薄弱位置产生疲劳开裂，这将严重影响工业厂房的正常工作［3］。由于肩梁除了起连接上下柱的作用外，往往还兼做吊车梁的支座，承担吊车梁传递的荷载，这就导致了肩梁处应力较大且应力随吊车的运行不断变化。由于钢结构肩梁采用大量连接焊缝，造成肩梁应力复杂且易出现应力集中，在反复荷载作用下易在薄弱部位开裂，发生疲劳破坏，直接影响吊车梁乃至整个厂房的正常工作。因此研究肩梁的疲劳失效机理，预测肩梁的疲劳寿命是有必要的。

本文结合一实际工程，采用有限元软件ANSYS-APDL建立钢肩梁的有限元模型，得到肩梁的应力云图，分析肩梁上各节点的应力状态，并得到肩梁的应力峰值点，尝试分析钢肩梁的疲劳失效机理，找到肩梁疲劳失效危险点。以疲劳失效危险点作为研究对象，得到其应力谱，通过雨流计数法处理后得到的荷载-频次图计算预测肩梁的疲劳寿命，计算方法采用S-N曲线法、线性累积损伤法、线弹性断裂力学法，并对几种方法得出的结果进行对比分析。最后分析肩梁腹板厚度及设置斜腹板对其应力状态的影响，并利用组合结构的优势设计一种组合结构形式的肩梁，对原肩梁结构进行优化。

1 肩梁静力分析

1.1 肩梁构造及其计算

某工业厂房一处单腹壁边柱肩梁，其设计简图及尺寸如图1 所示（其中t表示厚度），肩梁上盖板和下盖板厚20mm，通过螺栓连接垫板和吊车梁；右部连接实腹式上柱，上柱一侧翼缘在肩梁右端部，其荷载直接传递给下柱，上柱另一侧翼缘伸入肩梁兼做肩梁的横向加劲板，同时肩梁与吊车梁连接一端还焊有两块斜腹板呈八字形，其厚度为25mm。

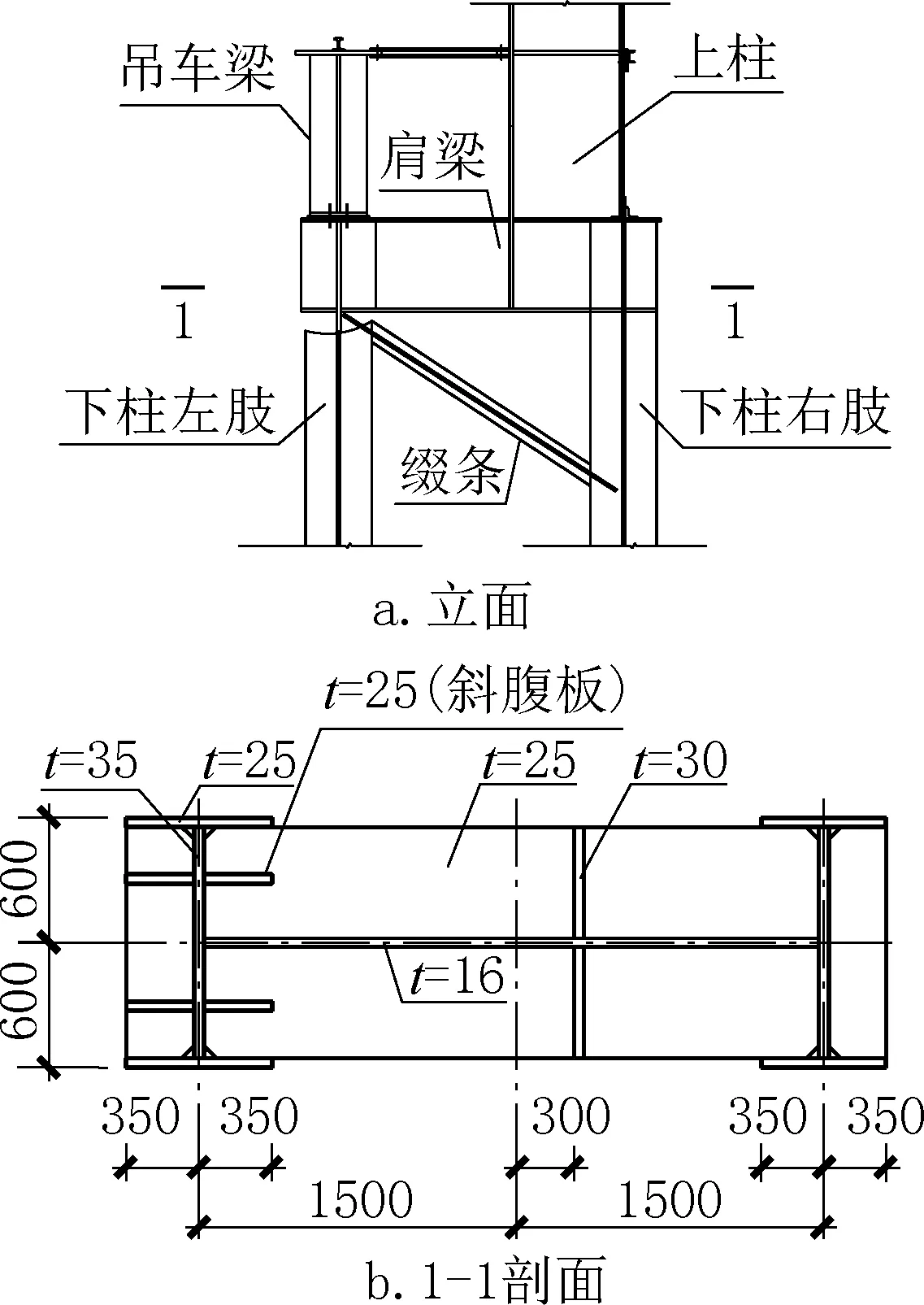
图1 肩梁构造Fig.1 Structure of the shoulder beam

该肩梁所受到的荷载主要是上柱传来的恒荷载以及吊车梁传来的动荷载；上柱传来的荷载为轴向力N1和弯矩M。吊车梁的荷载N2通过垫板直接传递给肩梁。肩梁的计算简图如图2 所示。

图2 肩梁计算简图Fig.2 Calculation diagram of the shoulder beam

肩梁所用钢材为Q420 钢，通过阶形柱的荷载计算可以得到上柱传来的荷载为轴力N1＝1504kN、弯矩M ＝1175kN·m，上柱为实腹式H型钢，其左右两侧翼缘形心之间的距离为h ＝1170mm，通过简化可以得到肩梁所受的两处等效集中力：

F1＝N1／2 +M／h ＝1756.27kN

F2＝N1／2 -M／h ＝-252.27kN

该肩梁所连接的吊车荷载如图3 所示。通过影响线计算可以得到当吊车满载且行驶到最不利位置时，吊车梁传递给肩梁的荷载最大为F3max＝3842.17kN，当吊车空载且行驶到最有利位置时，肩梁所受的荷载最小为F3min＝616.03kN。

图3 吊车荷载示意Fig.3 Schematic diagram of the crane load

上柱翼缘宽度为b1＝800mm，翼缘厚度为t1＝30mm，将上柱的集中力均匀分布在翼缘上得出均布荷载：

肩梁上盖板处焊接的垫板尺寸为b2L2＝700mm ×740mm，由于吊车梁与肩梁的约束关系为简支关系，故吊车梁荷载均布在垫板上，其最大、最小值分别为：

1.2 有限元建模与分析

采用ANSYS-APDL 进行肩梁的有限元建模，采用实体单元类型，建立肩梁模型和部分上柱及下柱模型，其中为了更好地传力，上柱为渐变式的梯形翼缘；下柱腹板宽度与下盖板宽度相等，下柱翼缘包裹在肩梁两侧。钢材弹性模量E ＝2.06 × 105MPa，泊松比μ ＝0.3，密度取ρ ＝7.85g／cm3；由于肩梁的构造较为复杂，且存在斜向的腹板，故网格形式采用正四面体；在肩梁上盖板的垫板处施加均布荷载P3max＝7.42MPa，在上柱两侧翼缘处分别施加均布荷载P1＝73.18MPa、P2＝-10.51MPa，考虑肩梁自重作用沿y轴正方向施加加速度9.8m／s2；在下柱两肢的底面分别添加所有方向约束。

图4 给出了肩梁的Mises 应力云图，结果表明：在肩梁的垫板处、下柱翼缘与肩梁上盖板连接焊缝处、肩梁斜腹板与上盖板连接焊缝处均出现了较大应力，其中肩梁的最大应力出现在下柱翼缘与肩梁上盖板的焊接端部，其Mises 应力为347.76MPa，应力较大，已经接近钢材的屈服强度，可见此处出现了应力集中。但从第一主应力云图中可以发现，该点处应力始终处于压应力的状态，由于疲劳破坏的机理是材料受拉开裂，在疲劳分析中认为压应力不会导致材料的疲劳开裂，故在后续的疲劳计算中可以忽略该点。拉应力最大值出现在垫板与吊车梁连接处，应力值为205.28MPa，在图4 的应力云图中拾取该点对应的Mises应力为207.07MPa，以该点作为疲劳破坏的危险点进行后续研究。

图4 肩梁的应力云图（单位： MPa）Fig.4 Stress nephogram of the shoulder beam（unit：MPa）

1.3 肩梁的应力谱

1.肩梁应力循环统计

参考12m焊接实腹式吊车梁的测试［4］，可以得到随机应力与最大应力之间的关系为σ／σmax的统计学参数，其均值为μσ／σmax＝0.573，标准差为σσ／σmax＝0.154。

为了得到肩梁的应力谱，本文通过Python的random库建立1000 个正实数随机数组作为随机应力，设置其均值为0.573 ×207.07 ＝118.65，标准差为0.154 ×207.07 ＝31.89。通过filter 函数将1000 个随机数中小于34.83MPa 和大于207.07MPa的数据筛掉，将剩下的应力值作为肩梁的随机应力值来模拟吊车正常运行时不同工况下肩梁的应力状态。

2.雨流计数法处理肩梁应力循环

利用Python中的rainflow 雨流计数法的程序包，将1.2 节得到的肩梁危险点应力带入运行即可得到通过处理后的危险点随机应力，将应力幅按大小分为若干区间，设置每一级荷载幅值相差10MPa，相同区间的应力幅在后续计算中按平均值考虑。各级应力幅及其所对应的频次统计直方图如图5 所示，去掉无效的应力幅数据后，计算其均值和标准差为μs＝72.26，σs＝33.87。

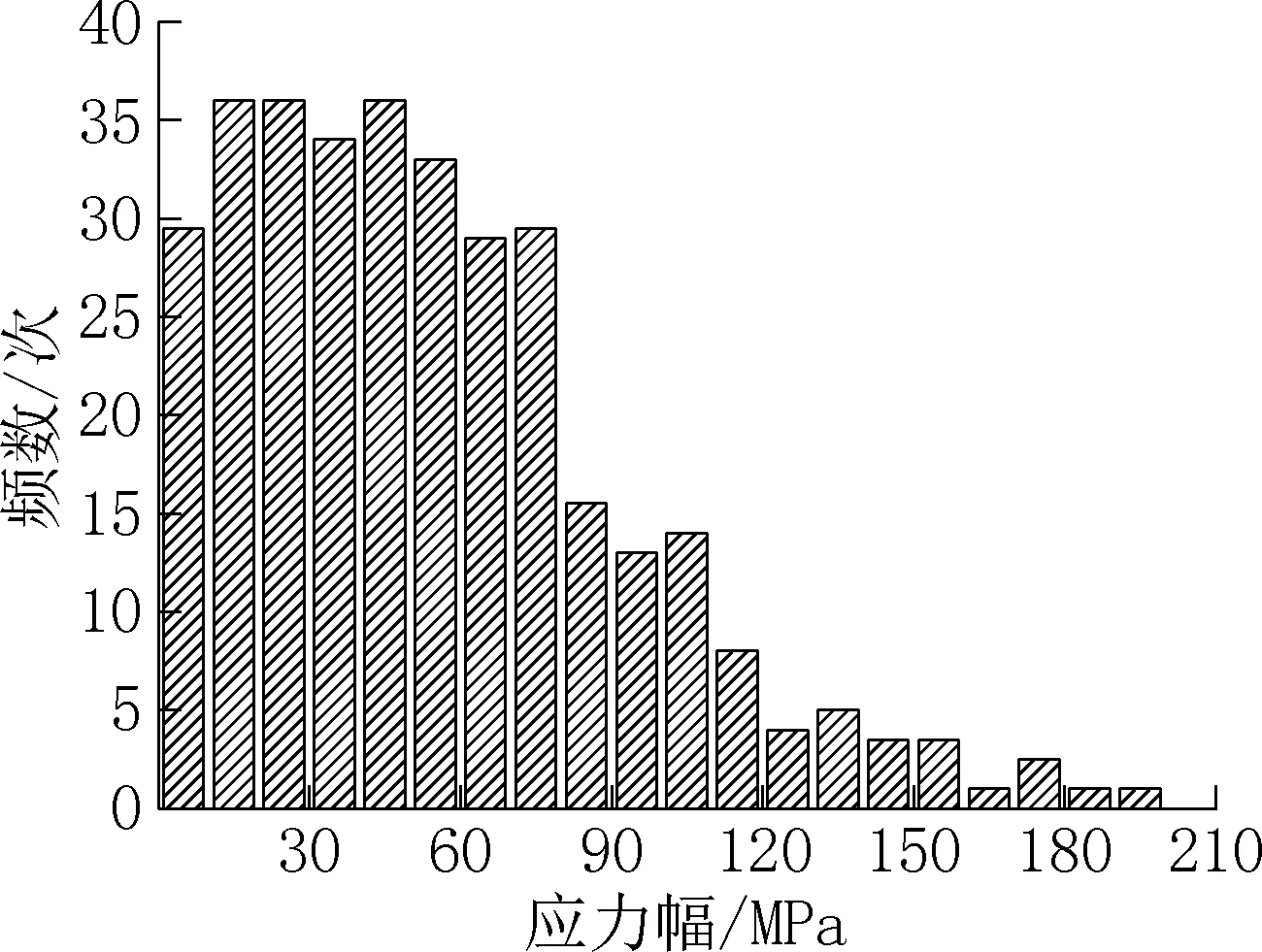
图5 肩梁的应力幅-频次图Fig.5 Stress amplitude-frequency diagram of shoulder beam

2 肩梁疲劳寿命分析

2.1 疲劳分析方法简介

1. S-N曲线法

S-N 曲线法是《钢结构设计标准》（GB 50017—2017）中规定并使用的一种疲劳寿命分析方法。该方法规定：当钢结构的构件及其连接直接承受动力荷载反复作用时，当应力循环次数n≥5 ×104次时，应当进行疲劳计算［5］。

2.线性累积损伤法

线性累积损伤法即认为结构或构件产生的各种损伤之间是相互独立的，且损伤产生的时间先后不会对最终结果造成影响。Miner 理论是一种典型实用的累积损伤法，将应力幅分为若干等级如Δσ1、Δσ2、Δσ3、Δσ4…，其对应的频次为n1、n2、n3、n4…。在各级应力幅单独作用下结构或构件的疲劳寿命为N1、N2、N3、N4…，这些应力幅造成的损伤占总损伤的比值为n1／N1、n2／N2、n3／N3、n4／N4…，称之为损伤率，当损伤率达到1 时，认为结构发生疲劳破坏。即：

3. 线弹性断裂力学法

由于材料表面划痕、合金中夹杂有害元素、焊缝缺陷等不可避免的因素影响，将导致在材料表面或内部往往会产生裂纹，此时实际情况的材料将不再完全符合规范中S-N曲线的规律了。断裂力学通过裂纹的发展规律和裂纹的长度来研究疲劳问题，更符合实际情况。

1963 年，Paris-Erdogan 提出了著名的Paris公式［3］，文献［4］在此基础上计算得到该方法的疲劳寿命表达式：

公式中符号的含义参见文献［5］。

2.2 肩梁的疲劳寿命分析与预测

在1.3 节中用雨流计数法处理得到的肩梁应力循环统计数据是本节疲劳寿命评估的依据，通过Python将2.1 节提到的三种方法编辑成程序，输入应力循环数据即可得到对应的疲劳寿命，其结果如表1 所示。

表1 各种疲劳分析方法预测结果统计Tab.1 Prediction results of various fatigue analysis methods

从结果上看，S-N 曲线法和线性累积损伤法的预测结果相同，线弹性断裂力学法的预测结果相对较低。由于S-N 曲线法是规范中采用的方法，作为结构设计的指导性方法，其结果应当相对保守，故结果相对较大，而线性累计损伤法从原理上与S-N曲线法中变幅应力幅等效为常幅应力幅的思想相接近，所以结果接近，由于新规范［6］中修正了等效应力幅的计算方法，导致两种方法从数学层面上等效；而线弹性断裂力学方法考虑了结构存在的初始缺陷，应该更接近实际情况，故预测结果相对较小。相关文献表明［6］，基于断裂力学的方法预测的结果一般更接近结构或构件的实际疲劳寿命。

一般吊车梁系统在一年中承受的应力循环次数为1.6 ×105次，该钢肩梁的疲劳寿命大概率将处于0.1 ×106到1 ×106 范围内，并不能满足工业厂房吊车梁全寿命周期内的正常运行，故对该肩梁结构进行优化设计是有必要的。

3 肩梁结构优化

3.1 参数优化

本文通过增加上盖板厚度及设置斜腹板来研究肩梁应力值的变化规律，其中方案一：上盖板厚度增加10mm；方案二：设置斜腹板，上端与垫板边缘平齐。

图6a、b 给出了两种方案的有限元计算结果，从结果看，优化后的肩梁的等效应力峰值相较于原结构的347.76MPa 明显降低，在250MPa左右。两种方案均能明显地减小肩梁的应力值，即增加上盖板厚度、设置斜腹板等措施均能改善肩梁的疲劳性能，提高其疲劳寿命。文献［10］表明肩梁的八字形支撑（斜腹板）相对于竖直支撑能够较好地传递吊车梁荷载，因此考虑方案一和方案二相结合，即同时增加上盖板厚度和设置斜腹板，简称方案三，其有限元分析结果如图6c 所示。其等效应力峰值为234.75MPa，出现在上盖板与竖腹板连接处，该方案比前述两个方案应力值都更低，可以认为该方案更佳。

3.2 组合结构设计

原肩梁的构造形式复杂，且这种形式由于焊缝较多，易出现初始缺陷，在承受吊车梁传来的反复荷载时容易出现应力集中；虽然设置了八字形斜向加劲肋可以很好地传递吊车梁荷载，但由于肩梁上盖板和下柱翼缘中空导致肩梁受力时上盖板和部分焊缝连接处出现了不小的拉应力，这是造成肩梁疲劳失效的主要原因。因此本文最后提出一种简便的结构优化方式，即利用组合结构的优势，减少焊缝的使用，设计一种钢板约束混凝土组合结构肩梁。利用混凝土受压直接承受吊车梁传来的荷载。其设计简图如图7所示。具体做法如下：

图7 组合结构肩梁设计示意Fig.7 Design schematic diagram of composite structure shoulder beam

（1）去掉两块斜腹板，在下柱工字钢腹板两侧腔体中浇筑混凝土。

（2）为了约束混凝土，增加两块钢板焊接在下柱两翼缘之间，既起模板的作用，又将两个混凝土块完全被包裹在钢结构中。

（3）在肩梁上盖板上预留孔洞作为混凝土的浇筑孔，浇筑完成后再进行填补。

（4）在两侧钢板和上下盖板处均焊接栓钉，在栓钉上固定纵横双向的钢筋片，以防止混凝土与钢材在受力时因为变形不协调而相对滑移。该结构形式利用组合结构巧妙地避免了肩梁的吊车梁连接端拉应力的出现，使吊车梁荷载直接传递给混凝土使其受压；而四周的钢板约束了混凝土侧向变形，使其承载能力进一步提升。

通过ANSYS 对设计的组合结构肩梁进行建模分析，混凝土和钢材均采用实体单元solid186，钢材的材料参数与1.2 节相同，混凝土弹性模量E ＝3.00 × 104MPa，泊松比μ ＝ 0.2，密度取2400kg／m3。混凝土抗压强度设计值为14.3MPa。网格划分、边界条件及加载形式等均与1.2 节中相同。计算得到组合结构肩梁的应力云图如图8所示。

图8 组合结构肩梁的应力云图（单位： MPa）Fig.8 Stress nephogram of the composite structure shoulder beam（unit：MPa）

计算结果表明：优化后，原肩梁应力峰值点的应力明显降低，从肩梁的第一主应力云图中可以看出拉应力明显减少且应力值很低，连接吊车梁一端几乎全部受压，从Mises 应力云图中看出最大应力出现在肩梁右侧的上柱与肩梁下盖板连接处，由于该点的应力可以认为恒定不变，故不会对肩梁的疲劳寿命造成影响。

单独取出两个混凝土块得到的局部应力云图如图9 所示，由此可见混凝土的峰值应力为13.51MPa，小于其屈服强度，可以认为优化后肩梁的疲劳寿命明显提升。

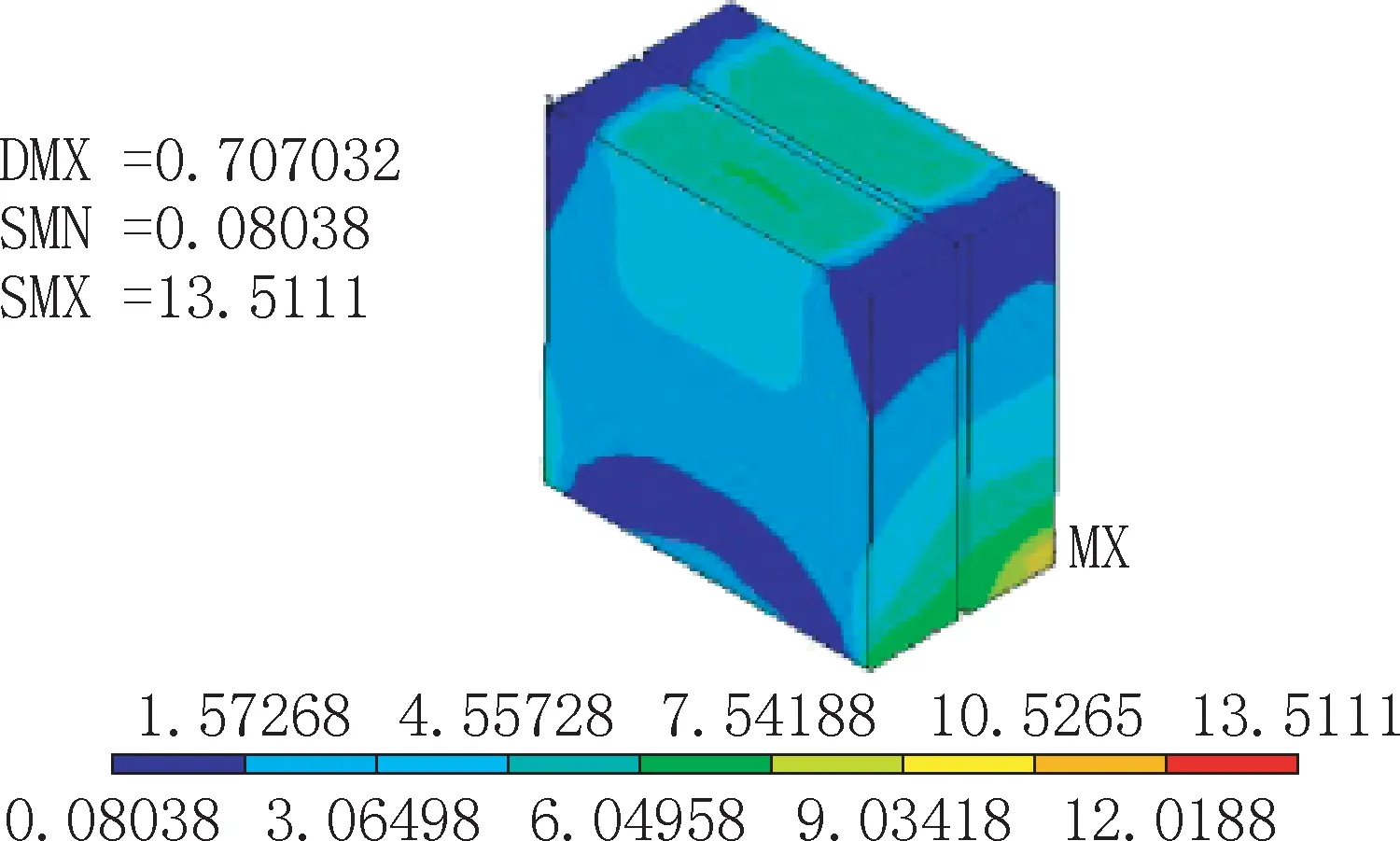
图9 混凝土块的Mises 应力云图（单位： MPa）Fig.9 Mises stress nephogram of the concrete blocks（unit：MPa）

4 结论

1. ANSYS-APDL计算结果表明：最大等效应力出现在肩梁上盖板与下柱翼缘连接焊缝处；但该点的第一主应力为负值即压应力，不会导致疲劳开裂；最大拉应力出现在垫板边缘，以该点作为危险点，通过雨流计数法处理该点应力数据，得到应力幅-频次数据。

2.采用3 种常用方法对肩梁疲劳寿命进行评估，结果表明S-N曲线法和线性累积损伤法预测结果相对偏保守，疲劳寿命较大；线弹性断裂力学法结果更接近实际。从总的结果上看，目标肩梁的预测疲劳寿命处于较低水平。

3.增加上盖板厚度和设置斜腹板均能有效降低肩梁的应力值，说明合理改变相关参数可提高肩梁的疲劳寿命，工程中可以选用其中之一，或两者同时采用。

4.采用钢板约束混凝土结构改造原结构肩梁，并建模分析，结果表明优化后的组合结构肩梁峰值应力明显降低，原危险应力点由拉应力变为压应力。可以认为采用组合结构可提高肩梁的疲劳寿命。