风力发电结构有限元建模及其地震响应分析

王雪平, 丁明轩, 黄 杰, 李万润*,2,3, 杜永峰,2,3

(1.兰州理工大学 防震减灾研究所, 甘肃 兰州 730050; 2.兰州理工大学 甘肃省土木工程减震隔震国际科技合作基地, 甘肃 兰州 730050; 3.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050)

随着可持续发展战略的实施，风力发电产业得到大力发展，兆瓦级风力发电机得到广泛应用.随着我国风力发电机装机总量的不断增加，其风力发电机本身及相关产业暴露出的问题也越来越多，构建合理的风力发电结构模型是风力发电机设计与研发的基础，这不但有助于研究风力发电结构的静动力特性，同时也为风力发电机整机振动控制打下研究基础[1].目前学者提出了许多风力发电机结构建模的方法并且建立了相应的模型.柯世堂等[2]利用ANSYS有限元软件以5 MW风力发电机为对象建立风力发电结构有限元模型，其中叶片和塔体均采用壳单元，机舱采用梁单元，并考虑土-结构相互作用，土体单元采用实体单元，利用COMBIN14弹簧单元模拟土体与基础之间的弹性作用.Ian等[3]通过足尺模型振动台试验和梁柱单元有限元模型考察了某65 kW小型风力发电塔的抗震性能，指出其动力响应以一阶振型为主.刘香等[4]、赵荣珍等[5]及马人乐等[6]通过建立“桨叶-轮毂-机舱-塔筒”整体风力发电结构的有限元模型，结合现场环境脉动实测数据，对比分析了风力发电结构的固有频率和阻尼.曹青等[7]和Li等[8]研究了风力发电结构在地震作用下的响应分析.Sadowski等[9]在考虑初始缺陷的情况下，对风力发电结构的地震响应进行了分析.金鑫等[10]基于多体系统动力学理论建立风力发电机风轮-塔架结构动力学分析模型，并基于此模型对风力发电整机系统进行了地震作用动力学分析.风力发电结构建模的过程中，各构件需要进行一定的简化，采用的简化方法不同，单元的选择也多种多样，采用不同精细程度的风力发电结构的有限元模型进行风机静动力学模拟时，其计算精度、计算效率呈现出一定的差异.因此，在进行风力发电结构的性能分析时，针对分析目的不同，选择合适的风力发电结构有限元模型就显得比较有意义.

本文在总结已有学者建立的风力发电结构模型的基础上，利用有限元软件ANSYS，建立了七种不同尺度、不同精细程度的风力发电结构有限元模型，并以地震响应分析为例，对比分析不同风力发电结构有限元模型在地震作用下的动力响应区别，为风力发电结构的分析和设计提供模型选择依据.

1 风力发电结构有限元模型

1.1 风力发电机基本参数

本文选用西北地区风力发电场中常见的2 MW三桨叶变桨距风力发电机作为原始模型.对于三桨叶风力发电机，三个叶片均匀汇集于轮毂，并与其刚接.轮毂与机舱刚性连接，机舱位于塔筒的顶端.该风力发电机的风轮直径为77 m(叶片扫过的直径)，单个叶片长度为44 m，叶片底端长度为3 m(叶片截面弦长值)，宽度(垂直叶片截面弦长方向)为0.8 m，叶尖截面长度为1.5 m，宽度为0.4 m.各叶片之间成120°夹角，额定转速为17 r/min.轮毂质量为12 t，叶片质量14 t，机舱质量为60 t，机舱外形为一长方体，长度为8.44 m，宽度为3.56 m，高度为3.4 m.风力发电结构高为80 m，塔筒为圆筒状，由三段组成，各段之间由法兰连接，其中塔底直径为4.1 m，塔底壁厚为25 mm.塔顶直径为2.5 m，塔顶壁厚为15 mm.塔筒厚度沿高度呈线性变化.在距离地面2 m的塔筒位置处，开有一门洞，其门洞近似呈椭圆形，长边方向为1.75 m，短边方向为0.75 m.风力发电结构的模型如图1所示.

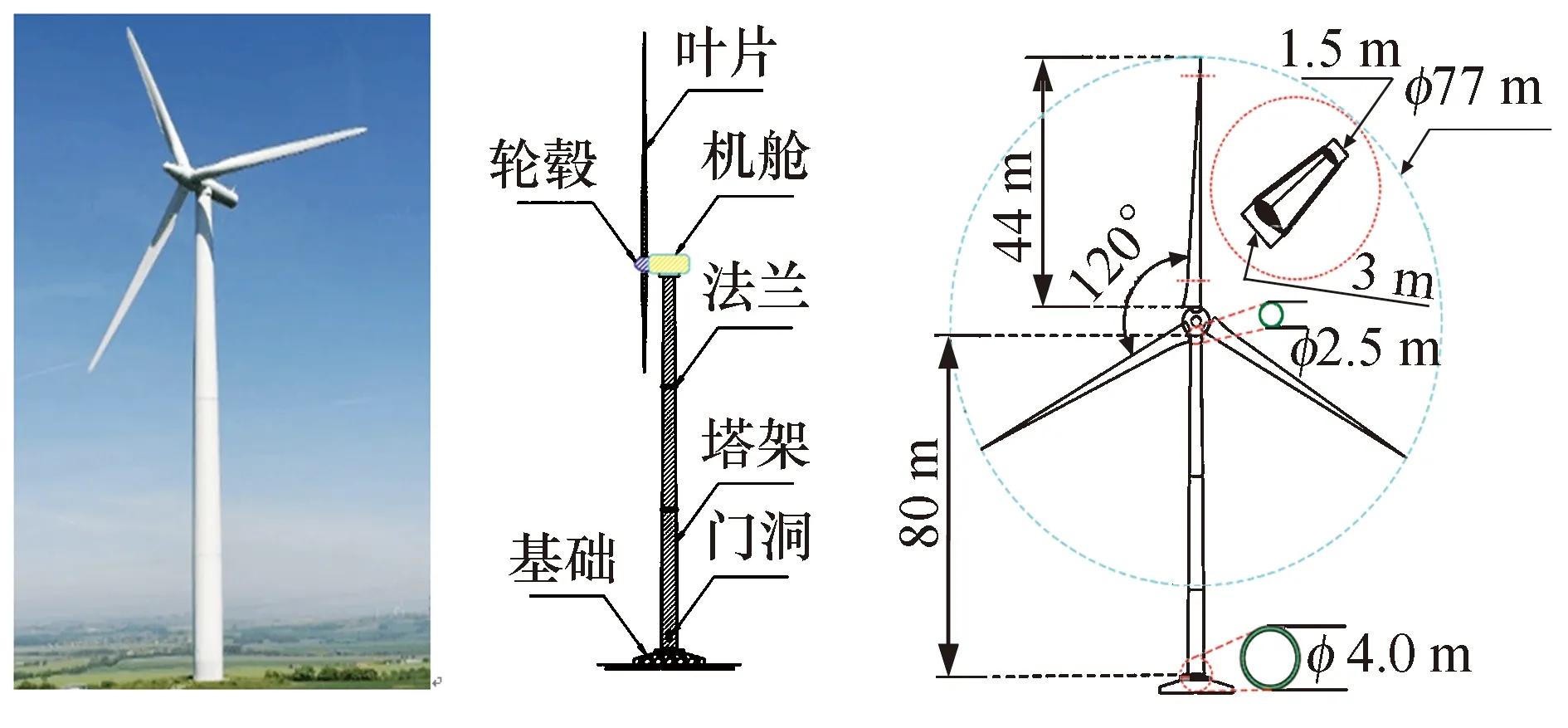
图1 风力发电结构模型

1.2 风力发电结构有限元模型

根据上述风力发电机的外形尺寸及材料属性，采用大型通用有限元软件ANSYS建立下列七种不同风力发电结构的有限元模型.

模型一：风力发电结构的塔筒用梁单元BEAM188模拟，设置变截面属性模拟塔筒厚度变化.对风力发电结构的叶片、机舱、轮毂进行简化，不考虑其对风力发电结构的影响，仅将其质量叠加，简化为集中质量点，采用集中质量单元MASS21模拟.采用CERIG命令，建立集中质量单元与塔筒顶端的约束，形成刚性区域.约束塔底节点的全部自由度，使其与地基固接.模型一的单元总数为81个，节点总数为82个.建立的风力发电结构有限元模型如图2所示.

图2 模型一有限元模型

模型二：风力发电结构的塔筒采用壳单元SHELL181单元模拟.采用ASBA命令，建立风力发电结构门洞，采用LREFINE命令将门洞处局部网格细化.将塔筒截面厚度表示为塔筒高度的函数，得到变厚度塔筒.机舱、轮毂及风机叶片采用与模型一相同的简化方法，塔底与地面固接.模型二的单元总数为8 198个，节点总数为4 143个.建立的风力发电结构有限元模型如图3所示.

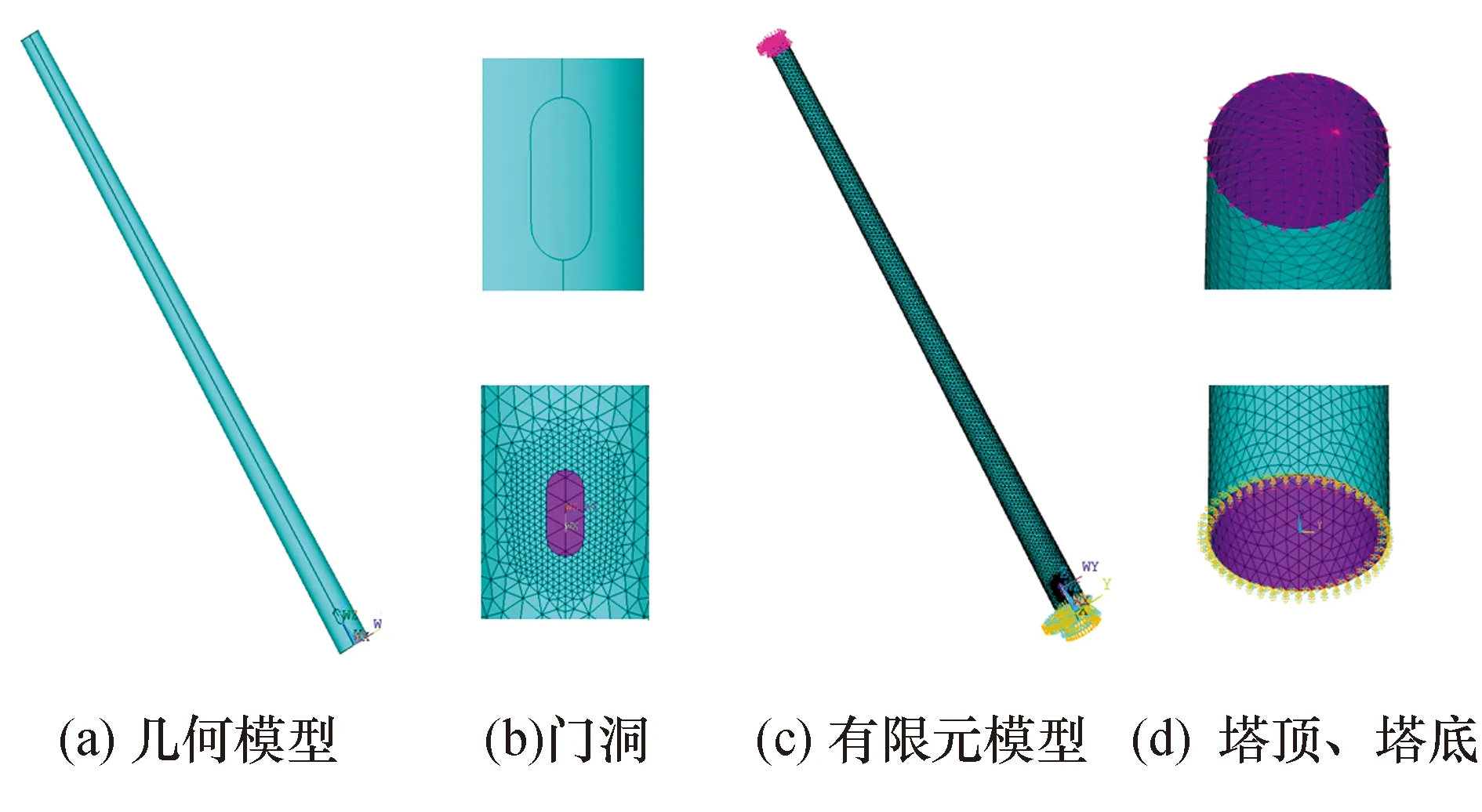
图3 模型二有限元模型

模型三：风力发电结构的塔筒采用实体单元SOLID95模拟，采用VSBV命令建立风机门洞以及门洞处的加劲肋，利用AREFINE命令将门洞网格细化，与加劲肋网格尺寸相当.机舱、轮毂及风机叶片同样采用MASS21单元模拟，塔底与地面固接.模型三的单元总数为83 410个，节点总数为159 830个.建立的风力发电结构有限元模型如图4所示.

图4 模型三有限元模型

模型四：考虑叶片、轮毂及机舱对风力发电结构的影响.采用梁单元建立各构件有限元模型，塔筒、机舱、叶片均采用BEAM188单元模拟，塔筒建模方法同模型一，将轮毂、机舱简化成一个整体，等效成长方体.利用旋转复制生成三个叶片.由于各构件之间采用相同单元，只需在连接处共用节点即可实现约束.模型四的单元数量为368个，节点数量为369个.建立的风力发电结构有限元模型如图5所示.

图5 模型四有限元模型

模型五：风力发电结构的塔筒采用SHELL181模拟，塔筒建模方法同模型二.叶片、机舱、轮毂采用BEAM188模拟，其建模方法同模型三.板壳单元实际具有5个自由度，其面内转动自由度ROTZ与梁单元的转动自由度意义不同[11].以机舱梁单元的节点作为主节点，选择塔筒顶端80 m高度处的所有节点为从节点，建立约束方程，实现两单元之间的耦合.模型五的单元总数为10 043个，节点总数为10 069个.建立的风力发电结构有限元模型如图6所示.

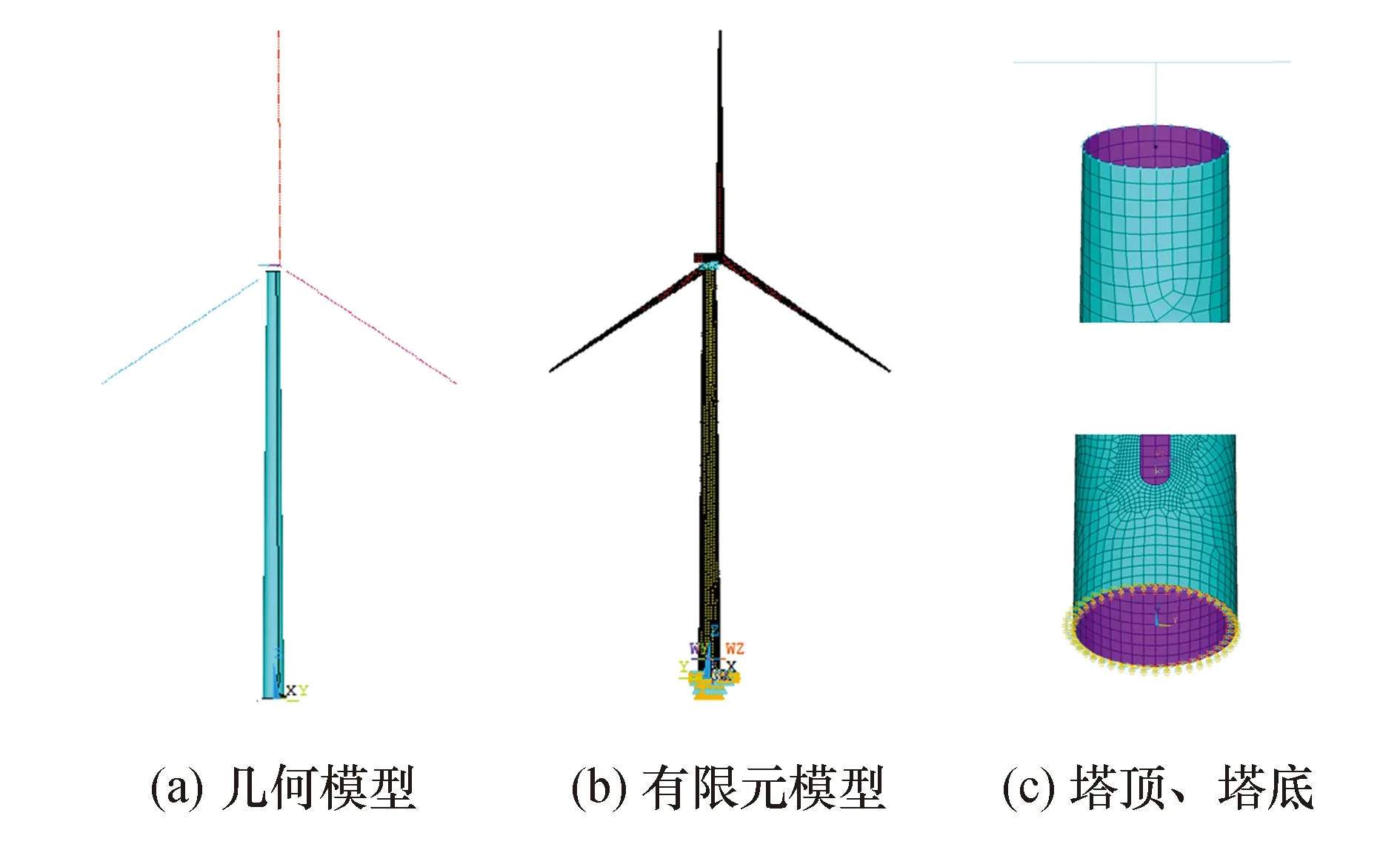
图6 模型五有限元模型

模型六：风力发电结构的塔筒采用SHELL181单元模拟，塔筒门洞位置处，采用实体单元模拟，使厚度方向的1/2处与塔筒曲面边缘接触.网格划分时，门洞位置实体单元采用局部网格细化，建立门洞局部精细模型.模型六的单元总数为8 446个，节点总数为6 487个.建立的风力发电结构模型如图7所示.

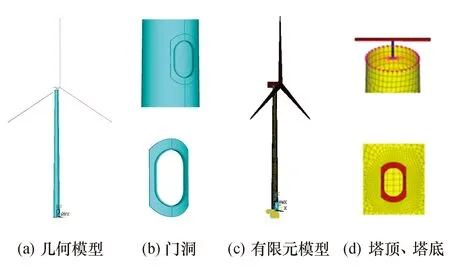
图7 模型六有限元模型

模型7：风力发电结构各组成部分均采用实体单元模拟，模型的单元数目为98 286个，节点数目为185 859个.建立的风力发电结构模型如图8所示.

图8 模型七有限元模型

2 风力发电结构地震响应分析

2.1 地震波选取

该风力发电机位于甘肃酒泉千万级风电场，该地区的抗震设防烈度为七度，设计基本地震加速度值为0.1g，所属的设计地震分组为第三组，场地类别为Ⅱ类.特征周期为0.45 s[12]，选取5条天然地震波和2条人工地震波.对选取的7条地震波的频谱特性、加速度幅值进行调整，选取地震波的持续时间均在30 s以上.对选取的天然地震波的频谱特性、幅值和持续时间进行调整，以满足规范设计要求.由于篇幅关系，此处只列出1条人工波及1条天然波的加速度时程，如图9、10所示.

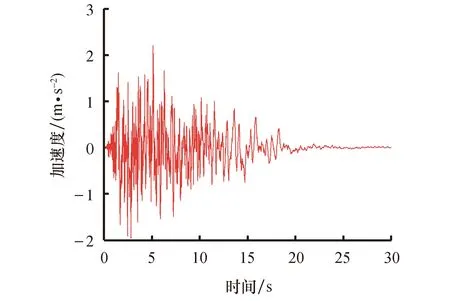
图9 人工波加速度时程

2.2 风力发电结构地震响应计算

风力发电结构的有限元模型建好之后，进入ANSYS瞬态分析模块，输入选择好的地震波数据，在计算之前，需设定风力发电结构的阻尼，本文采用实际工程中常用的瑞雷(Rayleigh)比例阻尼.在ANSYS中，粘性阻尼矩阵C表示为质量矩阵M和刚度矩阵K的线性组合：

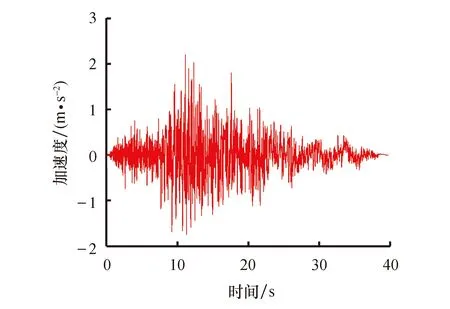
图10 天然波加速度时程

C=αM+βK

(1)

式中：α为质量阻尼系数；β为刚度质量系数.两个阻尼系数通过振型阻尼比得到.设ξi为某个振型的实际阻尼与临界阻尼之比，ωi为该模态对应的频率，则系数α和β存在以下关系：

(2)

对风力发电结构进行频率计算，得到结构前两阶的自振频率ωi和ωj，表1列出了风力发电结构模型前五阶频率.假定振型对应的阻尼比相同，即ξi=ξj=ξ.本文中风力发电结构的阻尼比取0.03.通过联立方程组，得到质量阻尼系数和刚度阻尼系数，从而设定风力发电结构的阻尼.

表1 风力发电结构前五阶自振频率

2.3 风力发电结构地震响应结果分析

2.3.1风力发电结构位移响应

计算完各模型在7条地震波作用下的响应之后，分别提取地震作用下各不同模型沿塔筒高度位移的最大值，得到风力发电结构模型的位移包络曲线，如图11所示，并提取出七个模型塔顶的位移时程曲线，如图12所示.

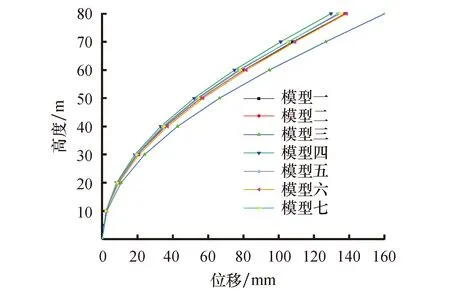
图11 塔筒位移包络图

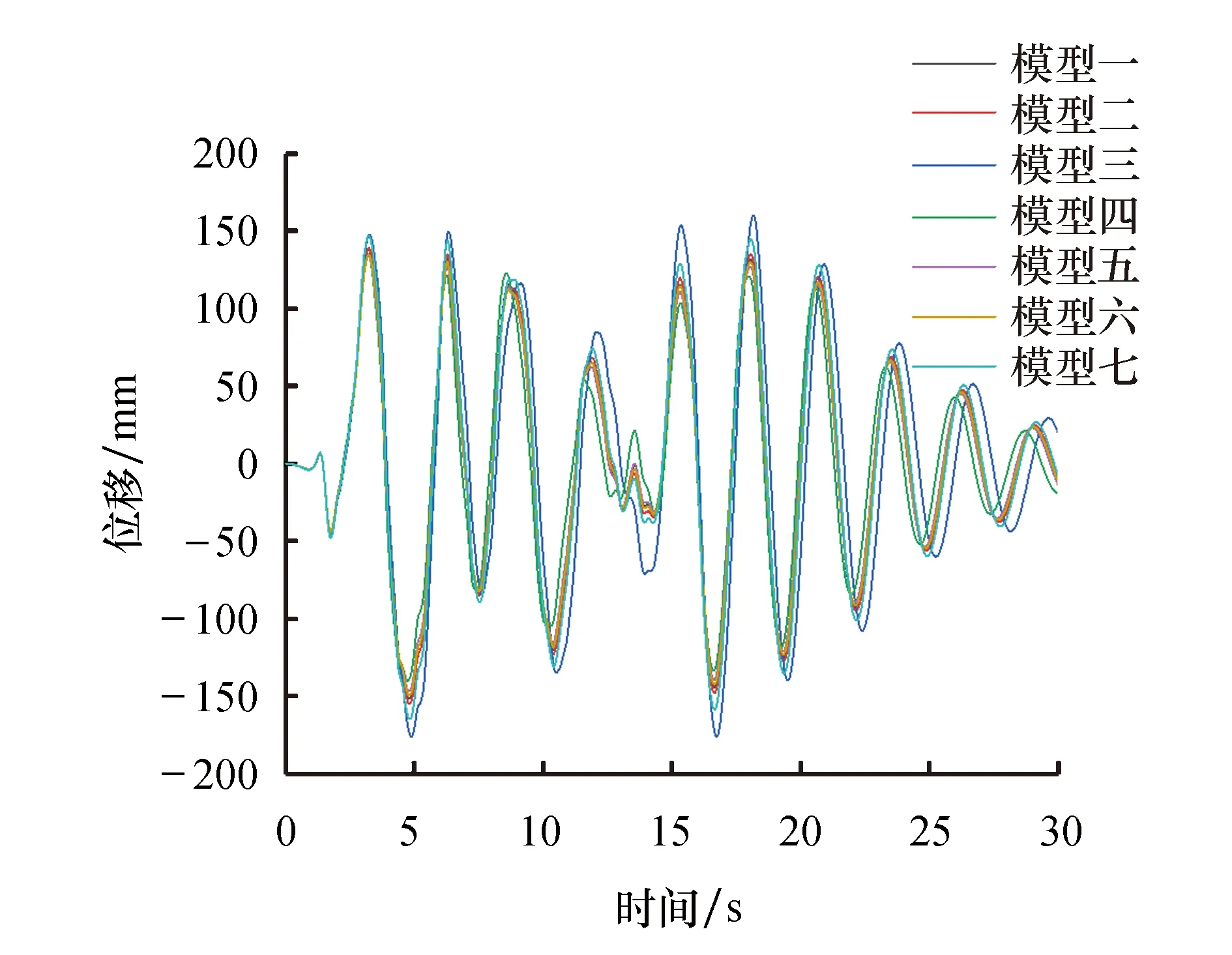
图12 塔顶位移时程曲线

由图11及图12可知，风力发电结构塔筒的变形为弯曲变形.其中模型三沿塔筒各位置处的位移最大，其塔筒顶端的位移值达到160.08 mm，模型四各位置处的位移最小，其顶点位移为129.598 mm，两者相差30.482 mm，其余模型的位移位于两者之间，其中，模型一、二、六的计算结果一致性相对较高.三个模型中模型一、二没有考虑叶片、轮毂、机舱的影响，而模型六考虑了其对风机的影响.由此可见，是否考虑风机的叶片、机舱、轮毂对地震作用下风力发电结构塔筒的位移响应影响不大.三个模型中模型六采用实体单元，计算代价最大，而模型一采用梁单元，其节点数目极少，计算效率最高.鉴于两者计算结果一致，因此在计算塔筒的位移时，可考虑采用模型一.

2.3.2风力发电结构内力分析

截面剪力和弯矩过大是造成风机倒塌的主要原因，风力发电结构截面的最大剪力和最大弯矩发生在塔筒底部.因此，提取各风机模型的塔底剪力和塔底弯矩时程曲线，如图13和图14所示，并得到各模型在整个地震响应期间塔底截面产生的最大剪力和最大弯矩.如表2所示.

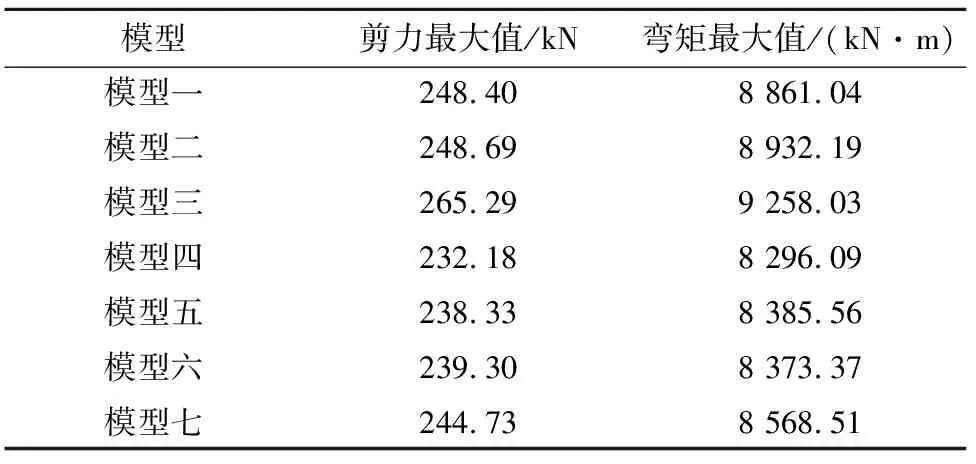
表2 塔底剪力、弯矩最大值

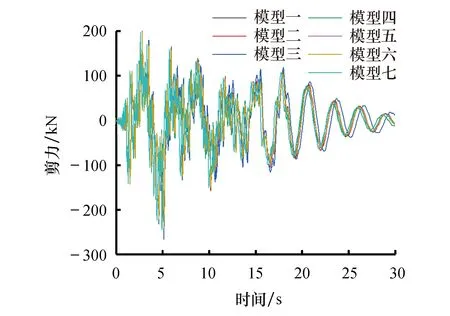
图13 塔底剪力时程曲线

图14 塔底弯矩时程曲线

从塔底剪力和弯矩时程曲线来看，各模型塔筒底端弯矩及剪力随时间变化的趋势基本一致.从剪力和弯矩的数值来看，模型三的剪力和弯矩最大值最大，模型四的剪力和弯矩最大值最小.两模型的剪力最大值相差33.106 kN，弯矩最大值相差961.94 kN·m，其数值相差较大.观察模型一、二、三和模型四、五、六、七可发现:考虑叶片、机舱、轮毂的模型比不考虑其影响的模型的剪力值和弯矩值大.观察不同单元类型建立的模型，发现采用实体单元建立的塔筒计算得到的剪力、弯矩值大于壳单元计算得到的值，壳单元相应的值大于梁单元的值.其中模型六的弯矩值比模型四大272.41 kN·m，模型三的弯矩值比模型一的值大396.99 kN·m.因此在进行风力发电结构塔筒截面内力计算时，应考虑叶片、轮毂、机舱的影响并优先选择高阶实体单元.

2.3.3风力发电结构应力分析

风力发电结构在地震作用下，塔筒应力过高会导致塔筒屈服，即使没有达到塔筒屈服极限，但是在地震往复荷载作用下，也有可能产生疲劳破坏.为此分别提取模型在7条地震波作用下沿塔筒高度方向的应力分布，最终得到塔筒的应力包络图，如图15所示，并得到塔筒40m高度处的应力时程曲线，如图16所示.

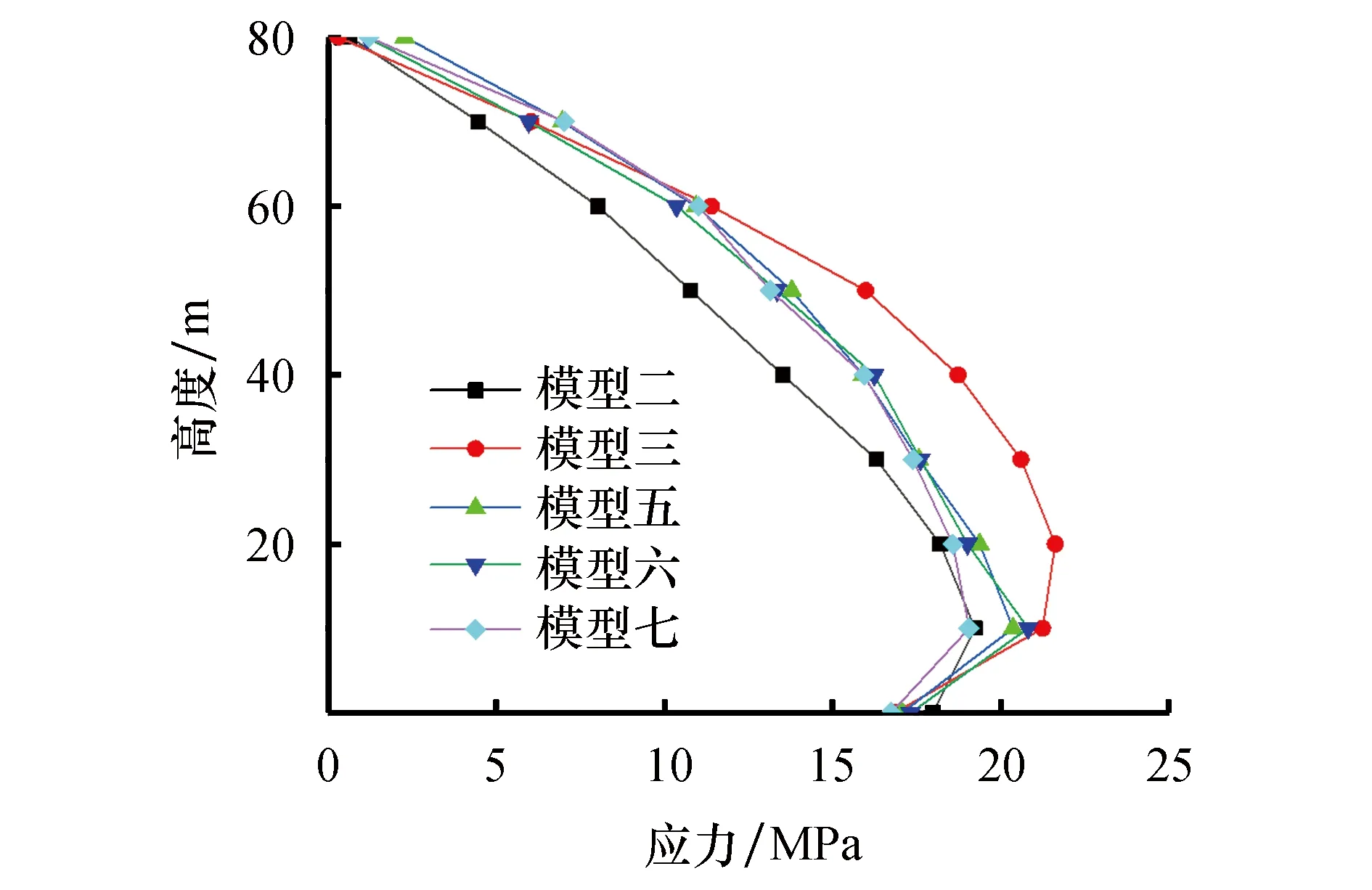
图15 塔筒应力包络图

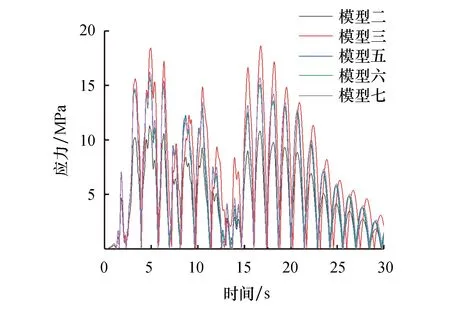
图16 40 m高度处应力时程

观察图15的塔筒应力包络图可知,塔筒的应力分布先从塔底逐渐增大，到达一定高度处塔筒应力达到最大值，然后沿着塔筒高度方向再逐渐减小，到达塔顶时应力达到最小值.各模型的应力最大值的数值及出现位置不同.其中模型三的应力最大值出现在塔筒20 m高度处，其余模型均出现在塔筒10 m高度处.模型三得到的塔筒应力值最大，模型二得到的应力值最小，两模型在40 m高度处相差达到最大，其差值为5.21 MPa.观察应力时程曲线，在整个时间历程内，模型三在40 m高度位置处的应力都大于其他模型，模型二的值则均小于其他模型，其结果离散性较大，这两个模型均为不考虑叶片、轮毂、机舱的影响，而其余考虑叶片、轮毂、机舱影响的模型的应力包络值在整个塔筒高度内其一致性较高.因此，在计算塔筒应力分布时需考虑风力发电结构叶片、轮毂、机舱的影响.观察模型五、六、七，其模型模拟的结果差别不大，因此采用壳单元仍能较好的模拟塔筒应力.

2.3.4风力发电结构应力集中分析

风力发电结构门洞开口位置处，易产生应力集中，产生较大的应力，可能会导致塔筒门洞位置处屈服.针对建有门洞的风力发电结构模型，提取门洞位置处的应力云图，如图17所示，得到门洞位置处最大应力点的位置，并提取各模型在该位置点处的应力时程曲线，如图18所示.

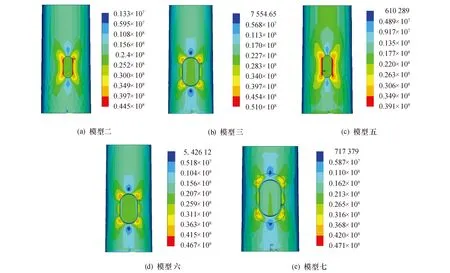
图17 塔筒门洞处应力云图

图18 应力-时程曲线

由应力时程曲线可知，各模型门洞应力达到最大值的时间发生在4.66 s.观察该时刻下的应力云图，模型的应力集中发生位置一致，分别位于门洞四个角点处.观察模型二、五和模型三、六，模型二比模型五应力增大13.8%，模型三相比模型六应力增大9.2%.其中模型二、五为不考虑叶片、机舱的影响，而模型三、六则相反，因此叶片、机舱对塔筒门洞处的应力影响较大.观察模型二、三和模型五、六的应力云图，采用不同单元对门洞应力影响也比较大，其中模型三、六采用实体单元，模型二、五采用壳单元.模型三相比模型二应力增大15.9%，而模型六相比模型二应力增大19.4%.而模型七中塔筒采用壳单元，模型局部采用实体单元，由此模型得到的门洞应力与模型六仅相差0.8%.可知此模型能较好地模型塔筒门洞处的应力.

3 结论

本文以风场中常见的2 MW三桨叶风力发电机为研究对象，采用不同单元、不同简化方法建立了七种不同精细程度的风力发电结构有限元模型.选择七条地震波，对风力发电结构的地震响应进行计算，从结构的整体位移、截面内力、应力及应力集中四个方面分析比较了各个模型的响应特点，得到的结论如下：

1)风力发电结构塔筒的变形以弯曲变形为主.各模型计算得到的塔筒位移值有所不同.模型三、四得到的位移结果相差较大，模型一、二、六的计算结果一致性相对较高.是否考虑风力发电结构叶片、机舱、轮毂对地震作用下风力发电结构塔筒的位移响应影响不大.计算塔筒位移时，采用高阶单元与低阶单元得到的计算结果差别较小.建议塔筒位移分析时可采用低阶单元.

2)各模型的塔筒底端弯矩及剪力变化的趋势基本一致.模型三的剪力和弯矩最大值最大，模型四的剪力和弯矩最大值最小，其数值相差较大.考虑叶片、机舱、轮毂影响的模型计算得到的剪力值和弯矩值较不考虑其影响的模型大.采用高阶单元计算得到的风力发电机塔筒的应力比低阶单元得到的应力准确.因此在进行风力发电结构塔筒截面内力计算时，应优先选择高阶实体单元.

3)塔筒的应力从塔底到塔顶逐渐增大，到达一定高度处塔筒应力达到最大值，然后沿着塔筒高度方向再逐渐减小，到达塔顶时应力达到最小值.各模型的应力最大值位置不同，不考虑叶片、轮毂、机舱影响的模型得到的塔筒应力分布在采用不同单元时的差异性较大.

4)各模型门洞应力变化趋势在地震过程中基本一致.各模型的应力集中均发生在门洞四个角点处.叶片、机舱对塔筒门洞处的应力影响较大，采用不同单元对门洞应力影响比较大，实体单元比采用壳单元应力增大15.9%，壳单元比梁单元应力增大19.4%.建议在应力集中分析中采用实体单元对门洞进行模拟.

致谢：本文得到兰州理工大学红柳优秀青年基金的资助，在此表示感谢.