极限载荷下风力发电机轮毂损伤分析

2022-11-07郑玉巧靳红红卢秉喜何正文

兰州理工大学学报 2022年5期

郑玉巧, 靳红红, 赵锋, 卢秉喜, 李浩, 何正文

(兰州理工大学机电工程学院, 甘肃兰州 730050)

轮毂作为风力发电机的关键部件，主要连接叶片和主轴，是受力情况最复杂(承受风力在叶片上的推力、扭矩、弯矩及陀螺力矩)且可靠性要求高的重要部件之一.其功能是将叶片承受的载荷经主轴传递至齿轮箱和机舱底座等关键部件[1-2].

风力发电机在运行过程中，轮毂承受着循环载荷与随机性载荷的双重作用，因此对轮毂进行强度分析和疲劳特性研究非常重要[3-6].在目前使用的风力发电机中采用3个叶片进行安装，通常按星形和球形结合的结构对外形进行设计.轮毂叶根处连接着具有加强腹板和变桨电机的安装座，驱动变桨达到变桨距功能，这种设计主要抵抗对称的风轮推力、3个叶片的单推力和3个叶片重力力矩.由于轮毂内、外表面的应力方向随载荷变化总在不断改变，所以载荷应力状态的复杂程度使得对轮毂的损伤研究尤为重要[7-8].通过对轮毂构件强度和损伤的研究，获得较高精度的耐久性和可靠性数据，对轮毂满20年疲劳寿命设计、成本控制以及整个风力发电机组的事故预防、维护维修均有重要意义[9-10].

本文首先对轮毂进行三维建模，将模型导入有限元软件中进行网格划分，并对网格划分进行介绍，满足网格划分要求;接着对轮毂模型施加载荷，载荷施加在叶根法兰处，使得轮毂在受力时接近于实际受力情况，并校核轮毂强度，研究轮毂在极限载荷下的损伤结果；最后优化轮毂结构[11-12].

1 相关理论简介

1.1 应力组合方法

VonMises等效应力通过应力等值线描述模型内部结构的应力分布状况，可清楚展现应力在模型的变化状态，便于快速确定模型结构中的最危险区域.VonMises等效应力为

(1)

式中：σSVM为等效应力；σAMP为最大主应力；σ1、σ2、σ3分别为第一、二、三主应力.

1.2 S-N曲线

S-N曲线是表征疲劳性能数据的经典方法，描述循环应力S与疲劳寿命N品之间的对应关系.描述S-N曲线的数学表达式通常有3种，即幂函数式、指数式和三参数式.其中,幂函数式的应用最为广泛，其表达式为

SmN=C

(2)

两边取对数后为

lgS=a+blgN

(3)

式中：S为循环应力，通常指应力幅值Sa或最大应力Smax；N为材料的疲劳寿命；m和C为材料的性能参数;材料参数a=lgC/m，b=-1/m.S与N是双对数线性关系.

1.3 平均应力修正方法

载荷谱和应力范围对构件材料寿命有着重要的影响，因而在应力循环中需对S-N曲线进行修正.对压缩平均应力不必进行修正，低韧性材料采用Goodman理论，即

(4)

式中：Sa为应力幅；Sm为平均应力；Su为极限拉伸强度；Se为应力比是-1时的应力幅.

1.4 Miner线性累积损伤理论

轮毂疲劳采用全寿命(S-N曲线)分析，以构件应力为基础，利用Miner线性累积损伤理论进行研究.轮毂在给定的应力水平反复作用下，损伤与应力循环可认为呈线性累积的关系.当累积损伤达到临界值1时，达到破坏准则，构件将产生疲劳破坏.在轮毂使用寿命内，风力发电机轮毂的累积损伤应力小于或等于1，即

D=∑ni/Ni≤1

(5)

式中：ni为在应力水平Si作用下的循环次数；Ni为在Si作用下循环至破坏的寿命.

对轮毂进行强度分析时，采用VonMises等效应力.疲劳分析时利用S-N曲线，并用Goodman理论修正平均应力，再结合Miner线性累积损伤理论分析轮毂损伤.

2 强度分析

2.1 坐标系的选取

选取合适的坐标系可简化风力发电机轮毂承受载荷的求解，用Bladed软件求出在极限工况下3个叶片根部法兰中心处的载荷.在叶根法兰中心建立节点，对每个节点施加极限载荷.施加载荷节点的坐标系采用GL规范中规定的叶片坐标系，坐标系方向如图1所示.

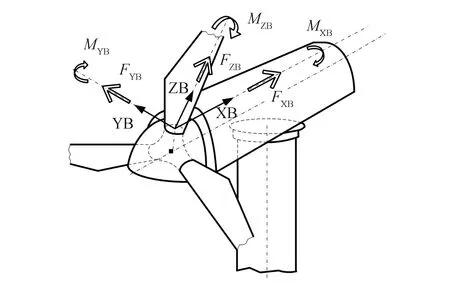
图1 叶片坐标系

图中,XB、YB、ZB分别为叶根坐标系的x、y、z轴方向，MXB、MYB、MZB分别为x、y、z轴3个方向的力矩，FXB、FYB、FZB分别为x、y、z轴3个方向的力.

2.2 研究对象和材料特性

叶片直径为1 375 mm，3个叶片间的横向距离为740 mm，轮毂中心到叶片的距离为986 mm.

通常轮毂材料采用球墨铸铁.本文球墨铸铁轮毂材料选用QT400-18，弹性模量为1.61×1011N/m2，泊松比为0.274，密度为7 000 kg/m3，屈服强度为2.5×108N/m2.

2.3 结构的网格划分

对于复杂零件进行网格划分，需要设置详细参数.本文采用的网格分析类型为显示分析(Explicit)，相关性Relevance=100，关联中心为Medium，平滑度为High，过渡为Slow.

网格划分法包括自动划分方法、六面体方法、四面体方法.在采用六面体进行网格划分时，要求过渡扭曲的面要少，并在曲率过大处设置过渡网格，这样生成的单元总数少，从而导致分析精度下降.为此，本文以常用的四面体单元对轮毂进行网格划分，并寻求合适的网格尺寸，分别以25、30 mm为单位对轮毂进行划分比对.网格尺寸为25 mm时，单元数为686 591，节点数为1 060 739;网格尺寸为30 mm时，单元数为455 233，节点数为712 654.由此可知，网格尺寸为30 mm时，单元数和节点数少，单元面的变形小，质量较高.因此,本文采用30 mm的网格尺寸.

2.4 载荷和边界条件的施加

轮毂所受载荷主要包括叶片的气动载荷、重力载荷和惯性载荷等.由于载荷通过与叶片根部连接处传递过来，所以计算轮毂所受载荷时以叶片的载荷理论为依据.风力发电机组各种关键部件的载荷计算采用GHBladed软件，其遵循GL风机认证标准[13].依据IEC61400-1的载荷工况，叶根处的极限载荷如表1所列.

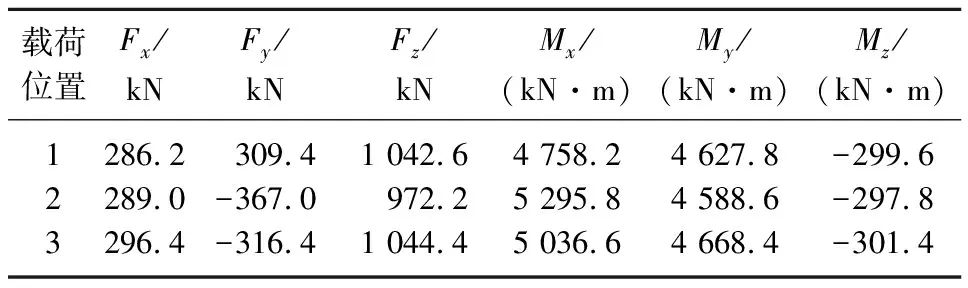
表1 极限载荷

在叶片坐标系下按6个坐标分量取6个单位载荷，分别加载到对应叶片法兰根部的导向节点上，3个叶片根部共18个单位载荷组成18个工况.轮毂的3个叶片法兰孔中心是承受叶片所传递载荷的位置.轮毂的载荷和约束如图2所示.

图2 轮毂的载荷和约束

可以看出：主轴与轮毂的连接面设置为固定约束，标记为A;将表1中的载荷按力和力矩的形式分别施加在相应叶片根部法兰端面中心处，B和C为施加载荷位置1，D和E为施加载荷位置2，F和G为施加载荷位置3.

基于轮毂的模拟加载过程(导入模型、添加材料、划分网格、施加载荷和边界条件)，求解得到轮毂的应力云图，如图3所示.

图3 轮毂的应力云图

可以看出，最大应力应变的区域在叶片法兰端面处，最大等效应力σmax=156.66 MPa.轮毂进行极限强度校核时，考虑铸造对其强度的影响，轮毂铸件系数取1.25.根据轮毂的载荷工况分析可知，轮毂局部安全系数rf=1.1.故轮毂材料(球墨铸铁)的局部安全系数ϒm=1.25×1.1=1.375，球墨铸铁轮毂的屈服极限σs=250 MPa.许用应力[σ]=σs/ϒm，从而[σ]=250/1.375≈181.8 MPa.轮毂在极限载荷下得到σmax<[σ],因而该球墨铸铁轮毂满足强度要求.

3 极限载荷下的损伤

疲劳寿命计算常用名义应力法，即以材料的S-N曲线为基础，以试件疲劳危险部位的应力集中系数和名义应力为参数，与疲劳累积损伤理论相结合，校核疲劳强度.S-N曲线不仅与材料的抗拉强度、屈服强度等力学性能有关，还与变异系数δ和材料的存活率P有关.风力发电机有关规定中轮毂材料的变异系数δ为10%，存活率P为95%.依据《疲劳强度与可靠性设计》得到QT400-18试样的S-N曲线，并提取存活率为95%的S-N曲线数据.轮毂疲劳寿命S-N曲线如图4所示.

图4 S-N曲线

可以看出：应力比为-1;循环次数在0～0.1×107时，交变应力随着循环次数的增大变化明显，应力越大寿命越长;循环次数大于0.1×107时，交变应力随着循环次数的增大变化趋于平缓，应力小于150 MPa时，轮毂不发生破坏.

轮毂承受载荷为交变载荷，破坏形式通常是疲劳破坏，轮毂设计满足静强度要求和疲劳寿命.使用ANSYS nCode DesignLife软件和Miner线性累积损伤准则计算整个轮毂表面的损伤，并列出分析结果中损伤最大的几个热点，给出没有时间序列压缩的损伤分析结果.7个热点的节点编号和对应的损伤值、寿命值如表2所列.

表2 热点损伤结果

可以看出：轮毂设计寿命为20年，即循环次数为1×107，球墨铸铁轮毂循环次数的最小值为5.269×1014，而5.269×1014>1×107，完全符合轮毂20年寿命的要求;另外，轮毂的最大损伤值为1.898×10-15，小于1，故轮毂在额定工况下运行安全.

通过分析发现，轮毂在承受极限载荷后，计算得到的最大安全系数为15.安全系数是极限应力与工作应力之比，当极限应力不变时，安全系数越大的构件区域工作应力越小.本文出现最小安全系数的部位是轮毂与3个叶片根部的法兰处，由此可知，该处的工作应力最大.

4 拓扑优化

拓扑优化是结构优化设计的重要组成部分，在给定的设计内实现设计模型最佳材料的均匀分布，依据构件所承受的约束条件、载荷情况和设计目标，寻求构件外形的最优拓扑结构[14-15].以轮毂结构减重和轻量化设计为基础，即以轮毂构件的质量为目标函数，在满足强度要求(最大应力不超过材料许用应力250MPa)的前提下使轮毂质量尽可能最小.

本文拓扑优化先导入模型,然后在static structure和topology optimization模块下进行.优化区域为整个轮毂模型，定义优化目标为90%的材料质量.拓扑优化求解结果如图5所示.