控制力矩陀螺转子框架耦合系统动力学分析

葛帅帅，曾四海，张志刚，石晓辉，黄剑鸣

(重庆理工大学 车辆工程学院， 重庆 400054)

0 引言

控制力矩陀螺(control moment gyro，CMG)通过高速旋转的转子获得一定的角动量,并通过改变角动量的方向对外输出控制力矩，具有输出力矩大、力矩连续可调、精度高、寿命长等优点[1-6]。近年来，随着微小型化的实现，CMG被应用到航空航天、两轮交通工具等领域的自平衡控制，并展现出特有的优势[5]。CMG转子高速旋转时，其转子的转动频率与自身固有频率重合，以及因转子加工和安装误差产生周期性不平衡激励，使得系统产生共振，不仅会产生巨大的噪声，还会造成结构失效。为了使控制力矩陀螺结构设计更加合理，系统运行更加可靠，有必要对CMG动力学特性进行分析[7]。

图1 控制力矩陀螺三维模型示意图

首先，去除转子、框架上不影响计算结果的倒角、小圆孔。其次，由于螺栓连接是高度非线性行为，故将螺栓连接处进行面面绑定处理。最后，由于加载在框架上的电机质量不可忽视，故将电机简化为一个质量点，并与框架耦合在一起[9]。

图2 轴承简化示意图

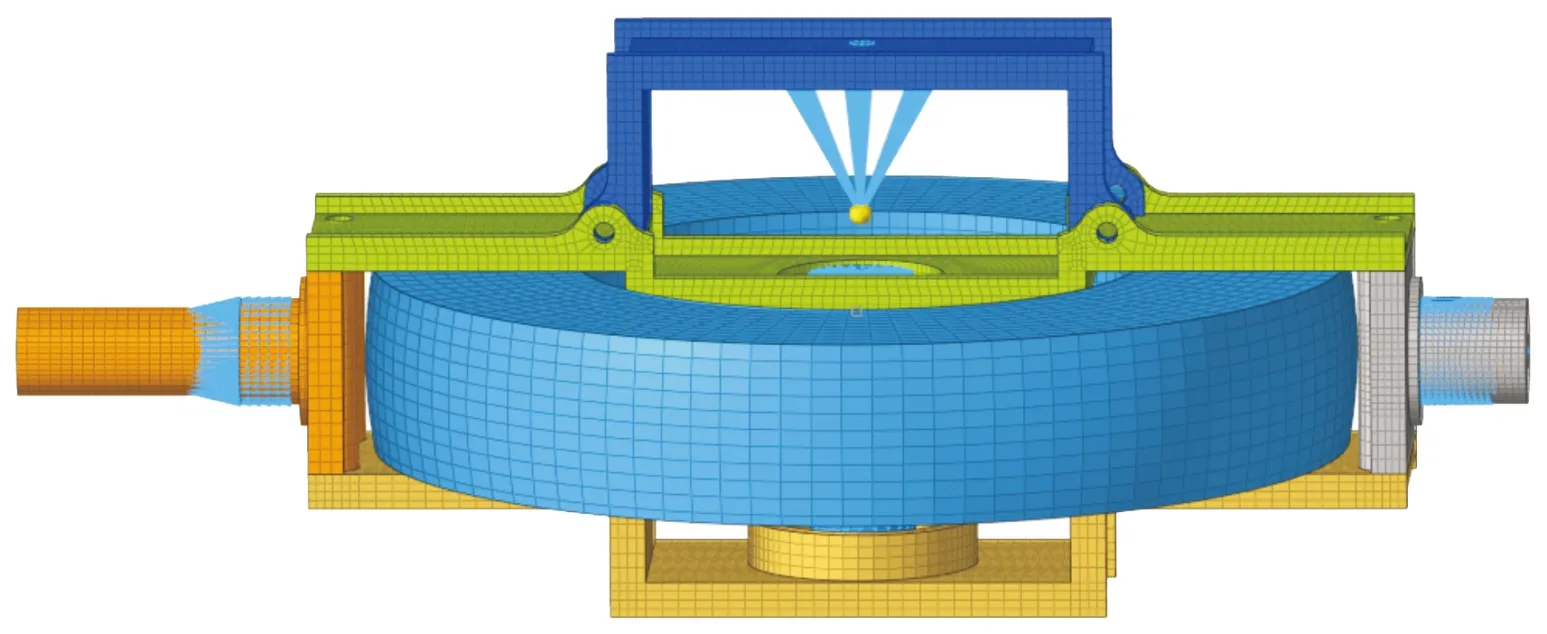
图3 控制力矩陀螺有限元模型网格示意图

2 转子、框架、耦合系统模态分析

2.1 模态分析理论

由于模态分析的是无阻尼自由振动，系统动力学方程为：

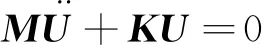
(1)

式中：M为结构质量矩阵;K为刚度矩阵。

式(1)存在非零解，通过线性代数变换，可得特征方程：

|K-ω2M|=0

(2)

当转子在自身不平衡激振力作用下升速或降速到某个转速时，转子固有频率接近该激振力频率，转子系统发生共振，导致系统发生剧烈振动，此时转子的转速即为临界转速[13]。临界转速ne与固有频率的关系如下式所示：

(3)

2.2 模态分析

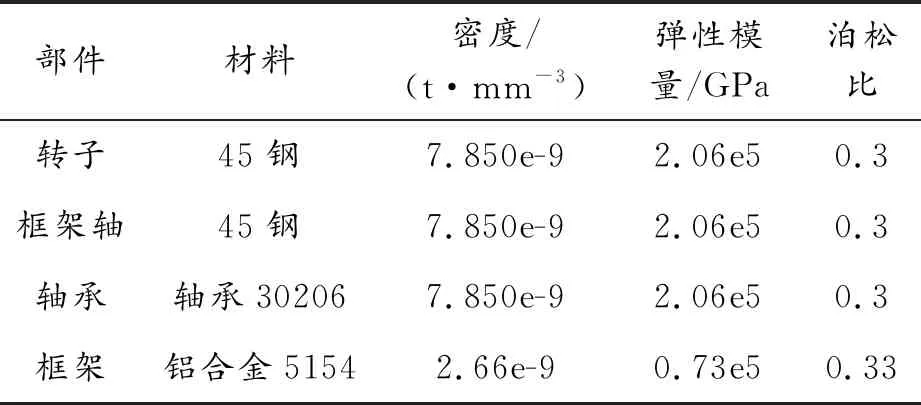
表1 材料属性参数

2.2.1转子模态分析

转子使用连接器固定两端轴，其前6阶模态频率及临界转速如表2所示。

表2 转子前6阶模态

高速转子稳定转速范围为10 000～15 000 r/min，稳定转频为166.67～250 Hz。由表中临界转速可知，转子前2阶共振频率处于转频之中，后4阶在转频之外，在前2阶模态频率下转子可能发生共振。前2阶模态振型如图4、图5所示，可以看出，转子的前2阶模态分别为沿z轴的轴向的平动振动和沿x轴的径向平动振动。

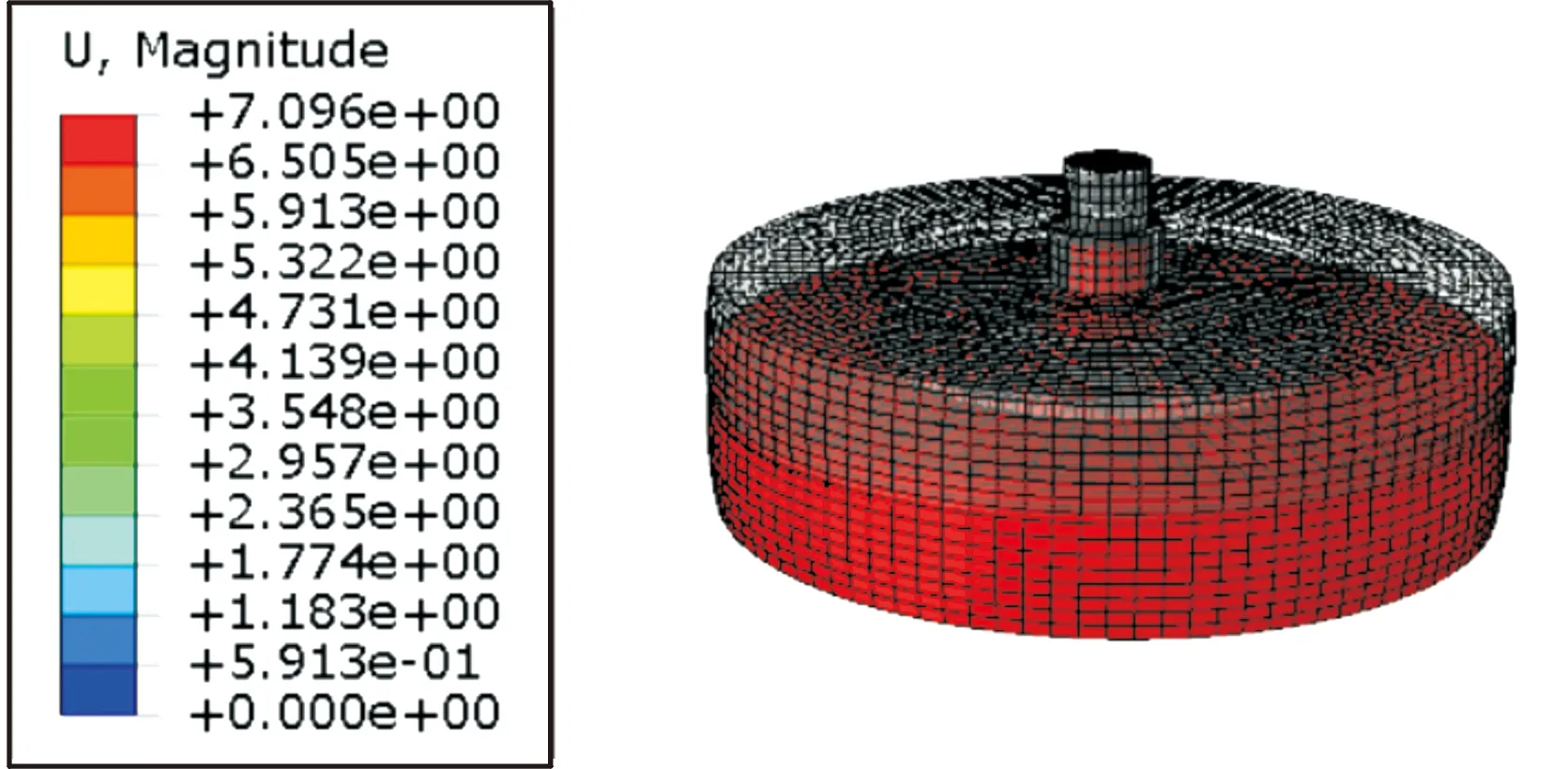
图4 转子1阶模态云图

图5 框架幅值模态曲线

图5 转子2阶模态云图

2.2.2框架模态分析

框架两端用连接器约束其自由度，得到其模态频率如表3所示。

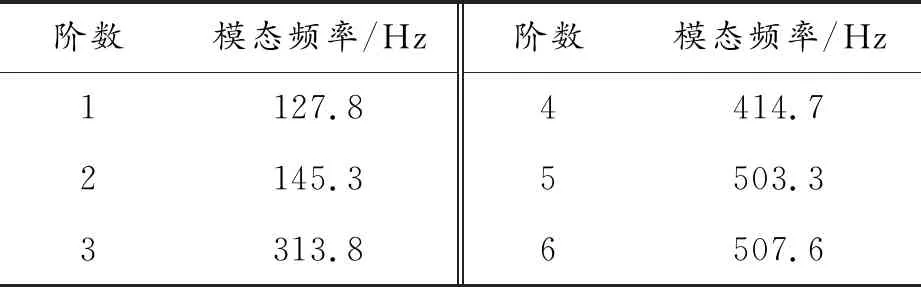
表3 框架模态频率

由表3可以看出，框架的前2阶共振频率在转频之下，后4阶频率在转频之外。框架前两阶模态如图6、图7所示，可以得出，框架第1阶振动主要为电机框架及下框架沿z轴的扭转振动，第2阶振型为电机框架和下框架沿y轴方向的扭转振动。

图7 框架2阶模态云图

转子与框架的耦合系统模态频率如表4所示。

表4 转子框架耦合系统模态频率

图8 耦合系统1阶模态振型

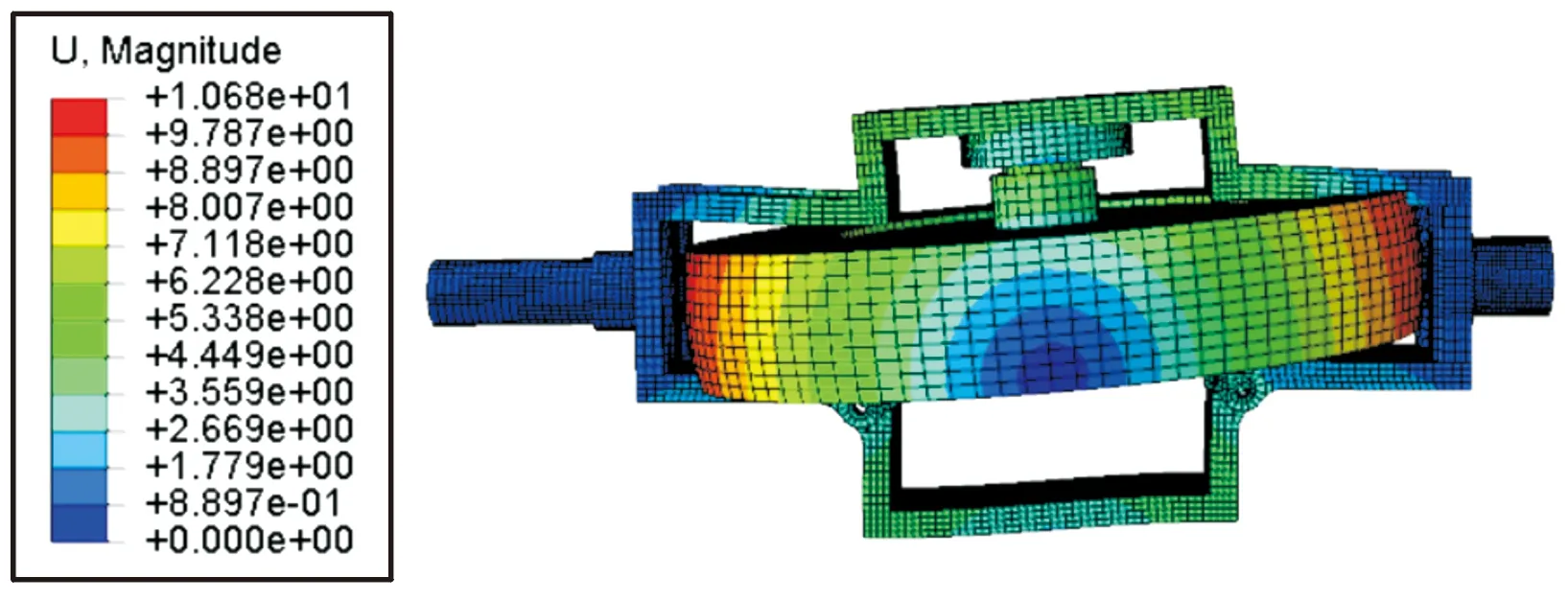
图9 耦合系统2阶模态振型云图

图10 耦合系统3阶模态振型云图

图11 耦合系统4阶模态振型云图

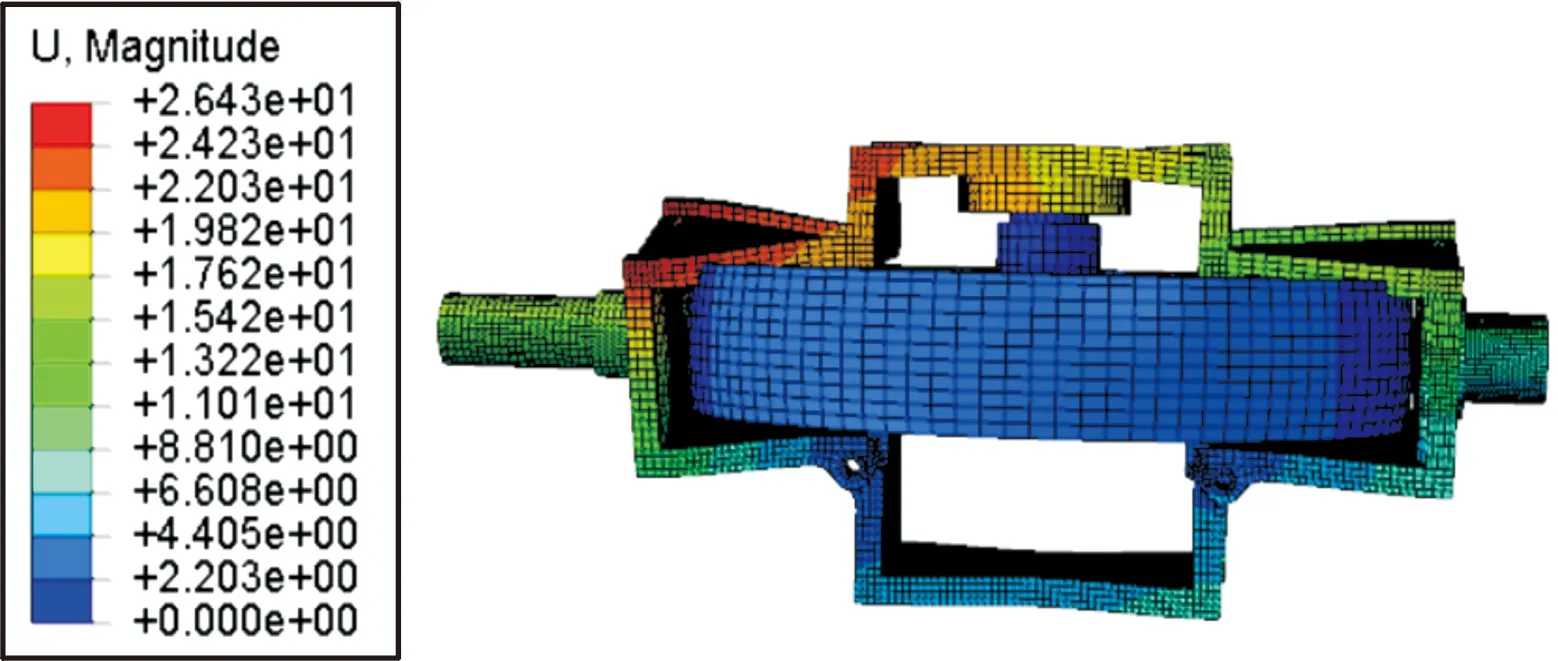
图12 耦合系统5阶模态振型云图

图13 耦合系统6阶模态振型云图

耦合系统第1阶模态主要为转子和上框架沿z轴的平移振动，2、3阶模态主要是转子和上下框架绕x轴的弯曲振动，4阶振型为框架在y方向的扭转振动，5阶振型为框架扭转振动，6阶振型为框架向中间的弯曲振动。在前4阶模态中，转子振动占主导作用，后2阶模态中，框架变形占主导作用。

表5 耦合系统频率下降幅度 %

耦合系统的第1阶频率相对转子下降62.5%，相对框架系统下降35.6%，第2阶频率相对转子下降42.8%，相对框架系统下降13.0%。用传统转子系统和框架系统分离的方法获得的动力学特性作为设计优化依据，会导致对共振发生频率评估偏高，无法在结构设计中有效避免共振产生，造成结构失效。

图14 转子幅值模态曲线

3.1 谐响应分析理论

转子不平衡质量产生的离心力Fe为：

(4)

式中：e为偏心距，mm；U为转子不平衡量，g·mm；ω为转子角速度，rad/s；n为旋转速度，r/min；m为不平衡质量，g；转子的额定转速为10 000～15 000 r/min，取最高转速进行分析。故有:

(5)

依据相似结构转子的试验数据，假设偏心距为0.2 mm，不平衡质量为100 g。

(6)

此转速下简谐激振频率为：

(7)

由于其绕z轴旋转，故在x、y方向产生不平衡简谐激振力Fx、Fy，其中：

Fx=Fesin(ωt)=24.7sin(2·π·250·t)

(8)

Fy=Fecos(ωt)=24.7sin(2·π·250·t)

(9)

3.2 谐响应分析及振动参与系数

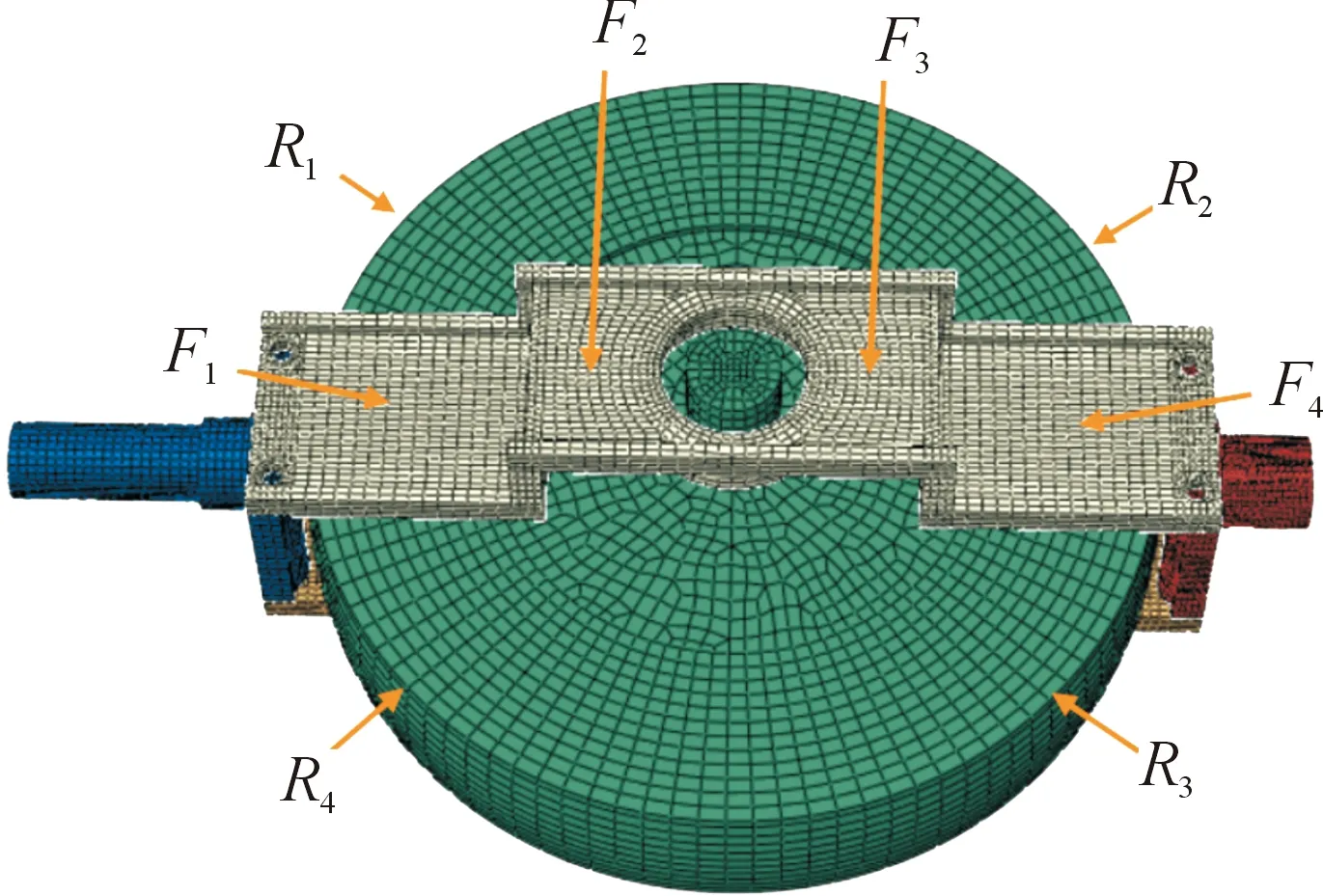
图16 点位示意图

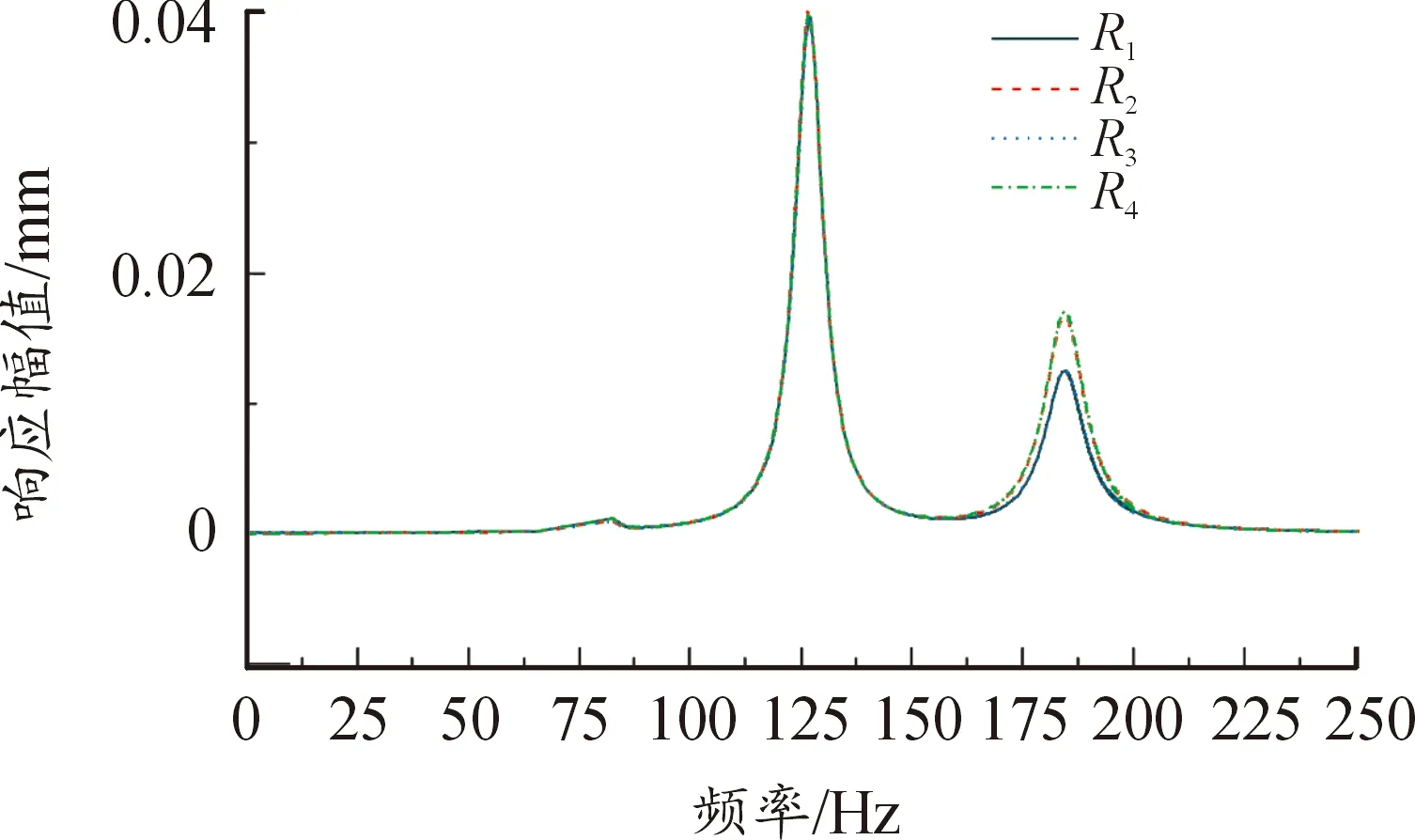
图17 耦合系统转子幅频响应曲线

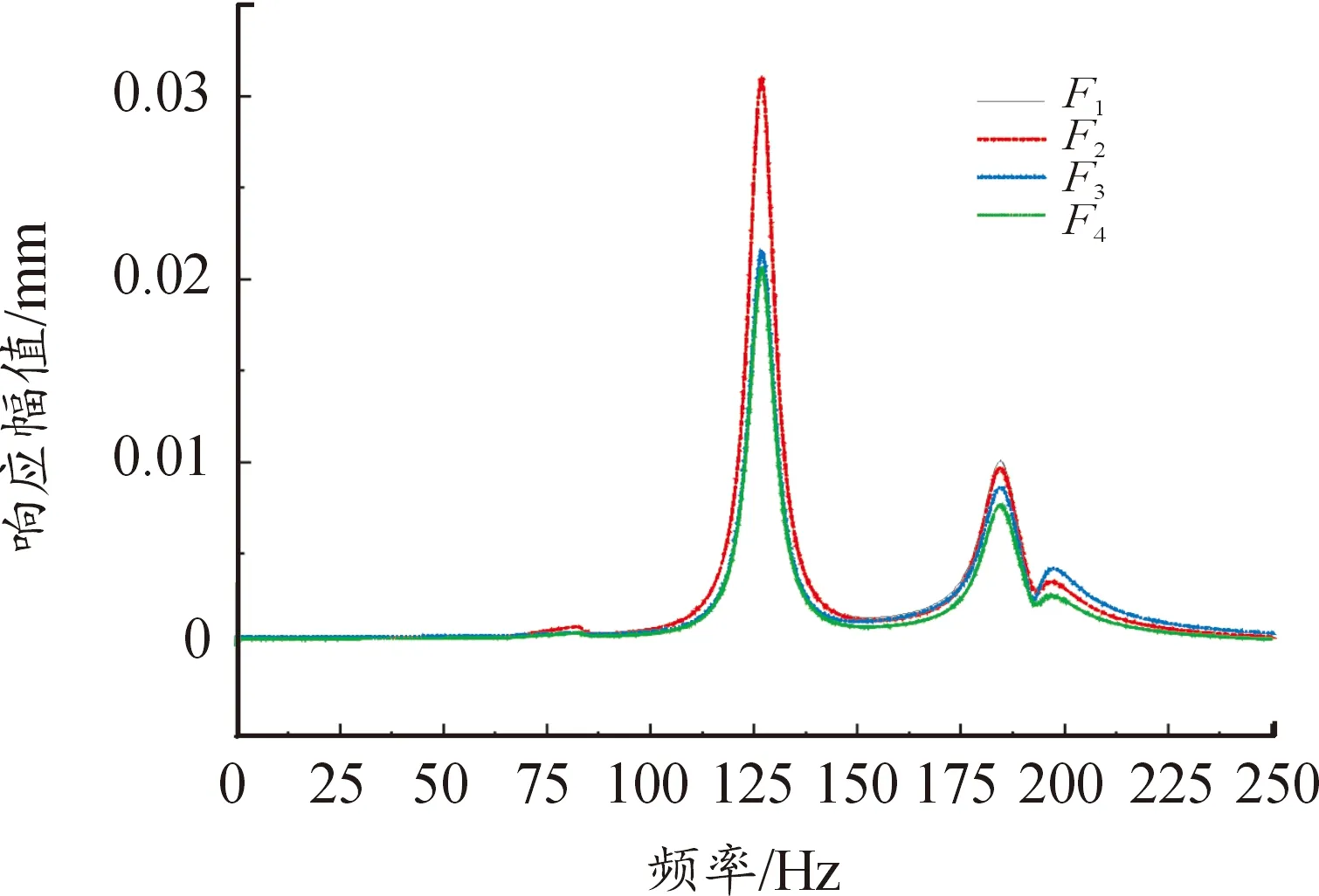
图18 耦合系统框架幅频响应曲线

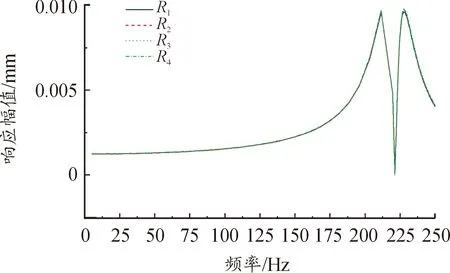
图19 单独转子幅频响应曲线

图20 单独框架幅频响应曲线

由幅频曲线可以看出，转子在210 Hz和 230 Hz出现“峰值”，框架在145 Hz左右出现“峰值”，而耦合系统中转子在126 Hz和190 Hz左右出现“峰值”，耦合系统框架在126、190、200 Hz时出现 “峰值”。 耦合系统“峰值”频率与其2阶、3阶和5阶、6阶共振频率重合，单独转子的“峰值”频率与第1阶和第2阶共振频率重合，单独框架 “峰值”只与第2阶共振频率重合。显然，在简谐激励下，不仅“峰值”频率出现的阶数不同，而且耦合系统“峰值”出现时的频率要明显小于单独转子和框架的“峰值”频率。此外，三者的“峰值”大小明显不同，耦合系统转子的最大峰值要比单独转子高75%，耦合系统框架最大峰值要比单独框架高77%，耦合系统在谐响应激励下，响应更加剧烈，对结构要求更高。

表6 振动参与系数

4 结论