基于仿人逻辑预测控制的自平衡摩托车系统研究
2022-11-07曾俊杰但远宏
徐 鹏,曾俊杰,但远宏,胡 斌,李 正,谭 智
(1.重庆理工大学 电气与电子工程学院, 重庆 400054;2.重庆理工大学 计算机科学与工程学院, 重庆 400054;3.重庆理工大学 车辆工程学院, 重庆 400054;4.重庆理工大学 机械工程学院, 重庆 400054)
0 引言
现如今摩托车已经成为一种非常有影响力的交通工具,由于其自身的不稳定性,以及在日常生活中的特殊应用,它通常被看作是简单的倒立摆,并且出现在了一些知识领域的研究课题中,如基础设施、系统动力学、控制系统等[1]。其中,系统动力学和控制系统为代表的控制力矩陀螺(control moment gyro,CMG) ,控制力矩陀螺是目前一种常用的执行机构,广泛用于船舶、航空、军事等。采用CMG的两轮自平衡摩托车是基于陀螺进动效应使车体实现自平衡,拥有了控制结构简单,并且能处于静态或者低速运行的状态。同时,还能在地势低洼,起伏不定的路况下运行,具有抗颠簸和撞击的能力[2]。
目前,学术界普遍认为两轮自平衡车的动力学模型是一种非线性、复杂性、时变性的欠驱动的失稳系统,所以相应控制策略的设计也成为了重要的研究点。自平衡车控制策略可分为传统经典控制和现代控制,以实现自平衡车的侧倾角度平衡。至今广泛应用的控制策略有PID控制器[3]、自抗扰控制器[4-5]、智能控制器[6]等。文献[7]中设计了一种粒子群算法优化的 LQR状态反馈控制器,有效提高了抗干扰力矩和抑制进动角耦合对系统的影响。文献[8]提出了反馈线性化方法将自平衡车的非线性动力学模型转换成线性动力学模型。文献[9-11]阐述了一种新型智能控制的仿人逻辑预测控制器,能够近似模拟有经验操作员控制的行为策略。文献[12]提出了一种滑模变结构控制器,能够有效使两轮汽车得以车身平衡,且具有强的鲁棒性。
本文采用了仿人逻辑预测控制法(humanoid logical predictive control,HLPC)控制力矩陀螺产生的力矩抵抗车体的重力矩,从而实现车体平衡以及陀螺框架进动角控制,此控制器是基于法布尔代数的逻辑控制与预测控制结合。当自平衡摩托车系统运行在允许的范围时,HLPC将在逻辑控制器与预测控制器切换,使系统能够快速朝平衡位置运动,从而加大了对CMG框架进动角度的控制力度,在减少系统超调量的基础上,也改善了车体横向抗扰动能力等。
1 CMG自平衡摩托车动力学模型
图1为自平衡摩托车机械结构示意图,力矩陀螺舱的中间安装2个力矩陀螺(CMG),分别为前陀螺和后陀螺,且CMG由2个框架稳固在力矩陀螺舱上,同时2个高速旋转电机带动前后陀螺,其次框架被2个伺服电机带动来改变水平方向。
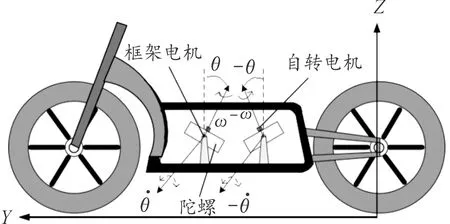
图1 自平衡摩托车机械结构示意图
1.1 力矩陀螺进动效应原理
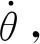
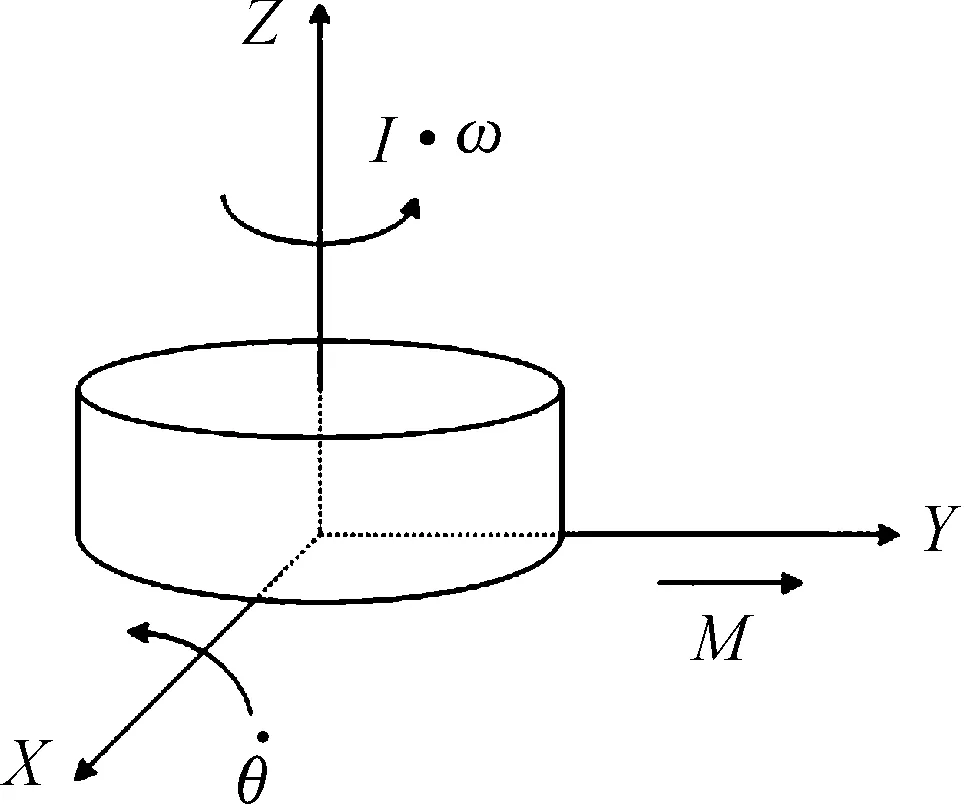
图2 力矩陀螺进动效应示意图
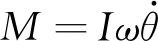
(1)
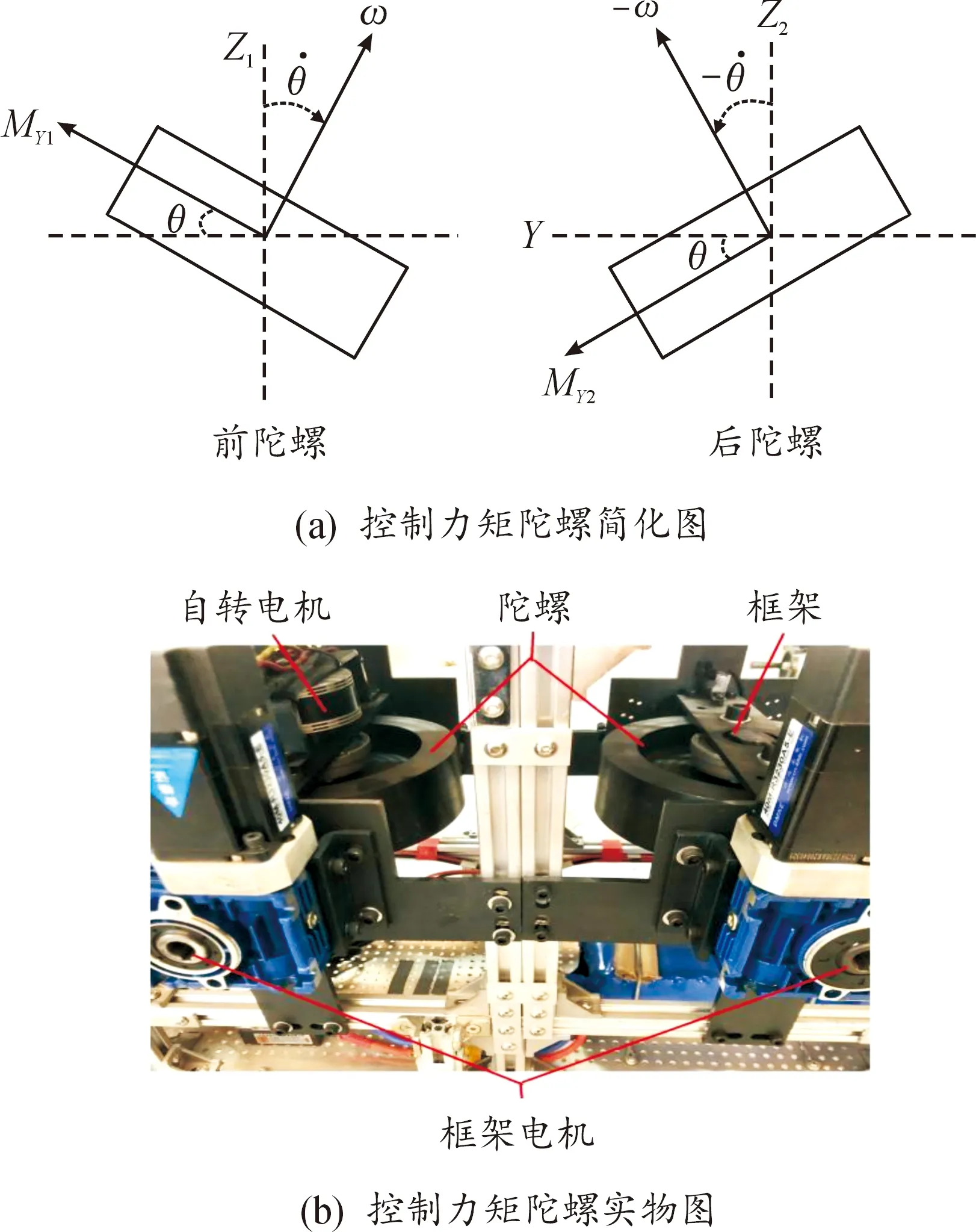
图3 控制两陀螺力矩示意图
(2)
由式(2)可知,当陀螺角度θ转动到90°时,进动力矩MY将变为零,此时力矩陀螺将不能维持车体平衡。
1.2 自平衡摩托车动力模型建立
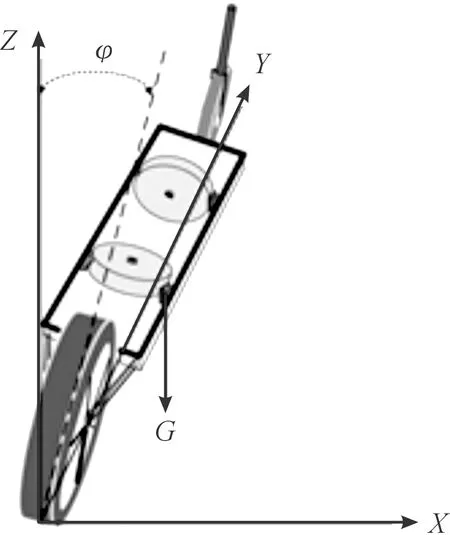
图4 车体侧倾角示意图
自平衡摩托车参数如表1所示。
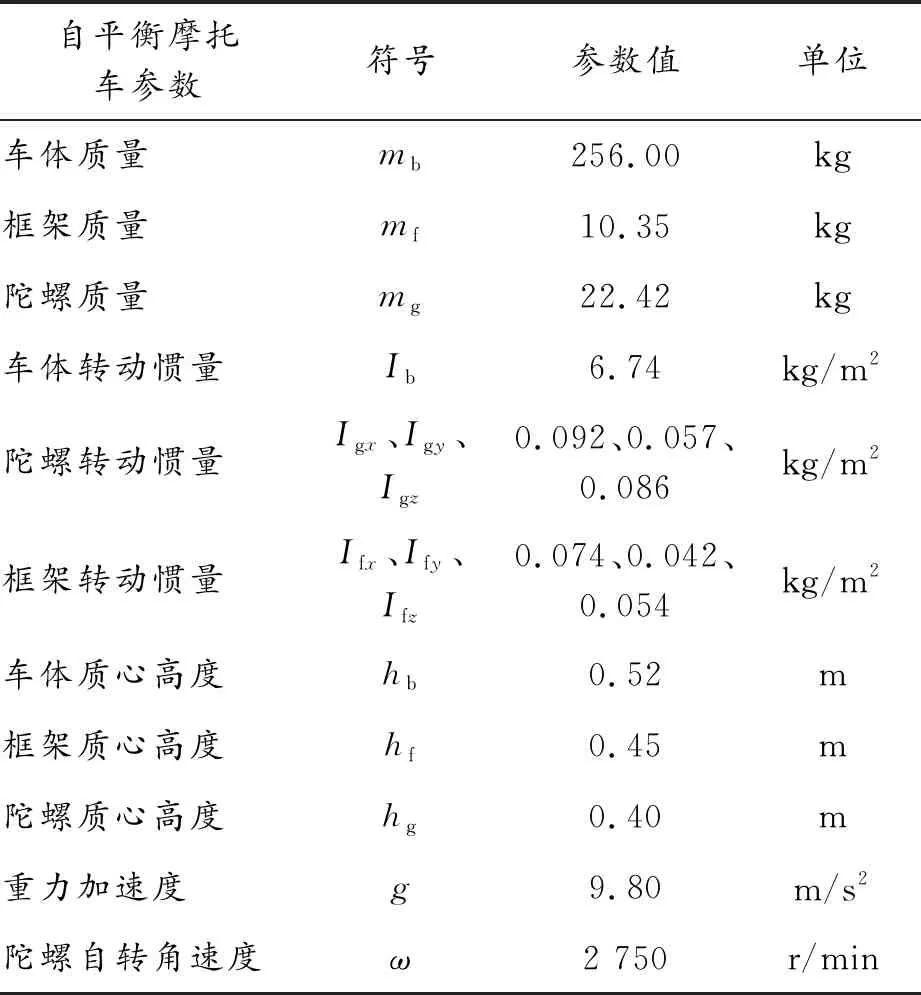
表1 自平衡摩托车参数
为了建立自平衡摩托车系统的状态方程,使用拉格朗日方程,如下式所示:
(3)
L=T-V
(4)
式中:L为拉格朗日函数;T为自平衡摩托车系统的动能;V为自平衡摩托车系统的势能,并且动能和势能是由车体、框架、陀螺主导的运动,qi(i= 1,2,3)为第i个广义坐标,Qi(i=1,2,3)为各广义坐标对应的广义力。
车体、框架、陀螺的线速度为:
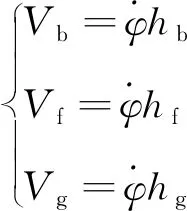
(5)
自平衡摩托车系统的车体、框架、陀螺动能表达式分别为:
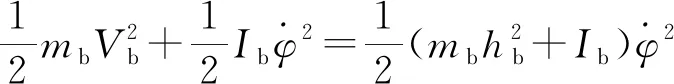
(6)

(7)
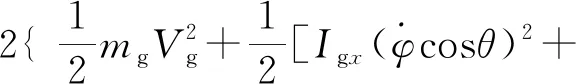
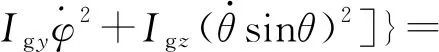
(8)
根据式(6)、式(7)和式(8)可得,自平衡摩托车系统的总动能为:
T=Tb+Tf+Tg
(9)
则自平衡摩托车系统的总势能为:
V=(mbhb+2mfhf+2mghg)gcosφ
(10)
关于φ、θ的拉格朗日方程如下:
(11)
(12)
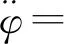
(mbhb+2mfhf+2mghg)gsinφ}/
2(Ifx+Igx)cos2θ+2(Ifx+Igx)sin2θ])
(13)

(14)
根据式(13)和式(14)可知,自平衡摩托车系统具有非线性耦合项,因此设计非线性控制器实现车体的自平衡非常困难。由于现实情况中,车体偏离平衡位置范围小,所以当车体处在平衡位置附近时,其可以处理成线性化模型:
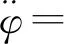
(15)
(16)
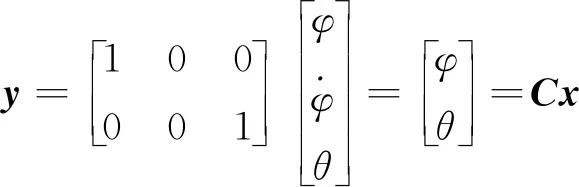
(17)
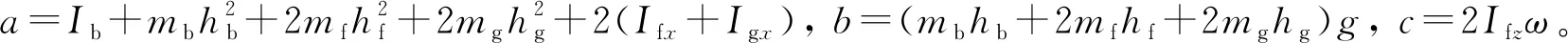
2 仿人逻辑预测控制器设计
HLPC是一种近似模拟有经验人员的策略控制器。逻辑控制是以闭环形式来对系统运行状态进行控制;预测控制是对人员经验的模拟。因此,将逻辑控制和预测控制的各自优点结合起来,不仅避免了逻辑控制器引起的超调问题,也提高了系统在失稳情况下的整体性能。
2.1 逻辑控制器


图5 9个区间的示意图

表2 坐标系区间
逻辑控制器的原型算法为:
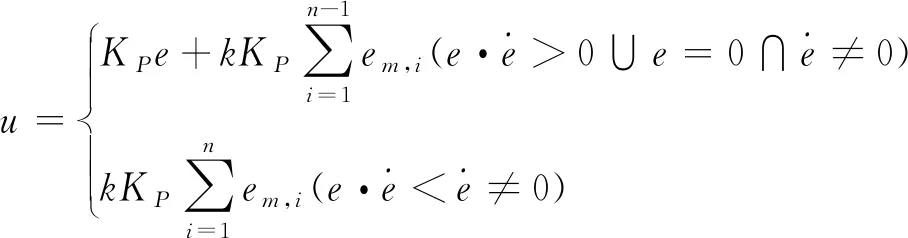
(18)
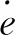
2.2 预测控制器
预测控制是依靠系统中被控对象的已往信息和当前信息,预测系统未来的输出量。
设MPC预测控制的模型输出为:

(19)
设系统中被控对象的模型表达式为:

(20)
将实际输出和预测输出之差作为预测误差 :

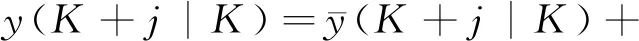
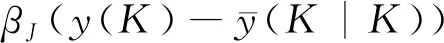
(21)
式中:H(l)H(l)为被控过程的单位阶跃响应;u(K-l)为系统输出的控制量;βj为反馈校正系数。
如果给定ys(K+j)作为系统期望的输出,那么系统的跟踪误差预测值输出为:
e(k+j|K)=ys(K+j)-y(K+j|K)
(22)
将式(21)代入式(22)得到:
e(K+j|K)=ys(K+j)-βjy(K)-
(23)
令u(K+i|K)=u(K+M-l|K),i∈{M,…,p-1} , 其中,M是控制时域,P是预测时域,一般选取M值小于P值。预测控制是为了求出未来系统控制输出u(K),需使得系统性能满足指标函数值最小,Q为误差权矩阵:
(24)
预测控制的实质就是计算出修正预测输出y(K+j|K)、跟踪误差预测值e(K+j|K)、第K步系统控制量输入u(K)。
2.3 仿人逻辑预测控制器
根据2.1、2.2小节对逻辑控制器和预测控制器的分析可以看出,2个控制器的组成是近似模拟人的思维特性,HLPC控制器结构如图6所示。

图6 仿人逻辑预测控制器结构示意图
从图6可以看出,系统开始工作时逻辑控制器和预测控制器同时运行。R(t)表示系统目标输入量,K(t)表示逻辑控制器的输出量,U(t)表示预测控制器的输出量,Y(t)表示控制对象状态输出量。逻辑控制的功能是在最短的时间内,将车体的倾斜角进入平衡状态,此时需要设置较宽的误差控制带;预测控制的功能是将车体的倾斜角稳定在平衡状态,为了使控制曲线品质达到最优,其将会在适当的时机,在这2种控制器的输出量进行切换。
具体来说,自平衡摩托车的侧倾角度偏离平衡位置,将通过逻辑状态判别其系统的运行状态,其控制量位于Ⅰ、Ⅱ、Ⅵ、Ⅴ 4种区间;此外,侧倾角度靠近平衡位置,其控制量位于Ⅳ、Ⅸ、Ⅷ 3种区间。
3 仿真实验与分析
为了进一步研究HLPC控制器的性能,基于Matlab/Simulink进行仿真验证,仿真步长为0.001 s。在不同静态偏置情况下,对摩托车分别进行自平衡及抗干扰仿真验证,且平衡位置设定为 0°,陀螺框架进动角度限幅在±45°。
3.1 静态自平衡仿真结果及分析
在车体侧倾角度为5°和10°的静态自平衡情况下,3种控制器作用下车体侧倾角度响应情况如图7所示。

图7 车体静态自平衡仿真曲线
从图7可以看出,车体的初始侧倾角度5°增大到10°,3种控制器都能够保证车体快速回到平衡位置。另外,PD控制器分别在1.7 s和2.6 s达到平衡状态;MPC控制器分别在1.8 s和2.5 s达到平衡状态;但是HLPC控制器分别在0.5 s和1.2 s就能够达到平衡状态,并且HLPC控制器的超调角度低于PD控制器和MPC控制器。
3.2 静态抗干扰仿真结果及分析
为了进一步展现车体抗干扰的能力,再次对车体侧倾角度设在5°和10°的静态抗干扰情况下,在第4 s时,对车体施加横向冲击干扰,以此来模拟车体在行驶过程中受到外界环境影响,则3种控制器的仿真结果如图8所示。

图8 车体静态抗干扰仿真曲线
从图8可以看出,3种控制器仍能使车体受到横向冲击后,均能保证车体回到平衡位置。但是,PD控制器和MPC控制器的偏离侧倾角度都比HLPC控制器大,其偏离侧倾角度分别为1.7°、0.9°、0.5°,且侧倾角度再次稳定到平衡位置的时间分别为1.1、2、0.5 s,HLPC控制器具有较好地抵抗横向冲击能力。
3.3 陀螺框架进动角度仿真结果及分析
车体的侧倾角度平衡控制过程中,同时伴随着陀螺框架进动角度的控制。图9为车体侧倾角5°和10°时,同步响应的陀螺框架进动角度仿真响应曲线。

图9 车体静态干扰下陀螺框架进动角度仿真响应曲线
从图9中可以看出,车体侧倾角度为5°和10°情况下,在3种控制器控制的陀螺框架进动角度变化过程中,分别达到最大的框架进动角度为15°和34°左右。当陀螺框架进动角度恢复到稳定时,再次受到横向冲击干扰后,PD控制器控制的框架进动角度为7.5°和23°,MPC控制器控制的框架进动角度为6.5°和16°,HLPC控制器控制的框架进动角度为4.5°和14.5°。结果说明了HLPC控制器控制的陀螺框架的稳定进动角度最小。
综上所述,自平衡摩托车侧倾角度和陀螺框架进动角度的控制中,HPLC控制器的控制效果优于PD控制器和MPC控制器,并且在静态自平衡和静态抗干扰工况下,拥有较快地恢复侧倾角度平衡和抗外部干扰能力。
4 结论
使用了一种新型的智能控制器——仿人逻辑预测控制器,该控制器的控制过程接近人的思维。使用2个力矩陀螺对车体的重力矩补偿控制,提高了两轮自平衡摩托车的平衡性能,仿真结果表明在静态自平衡和静态抗干扰情况下,HLPC控制器与PD控制器、MPC控制器相对,HLPC控制器能够快速地确保车体的侧倾角度恢复到竖直平衡位置以及控制的陀螺框架进动角度最小,能有效保证系统控制鲁棒性,为控制自平衡摩托车系统提供了一种新的智能控制手段。
