385 m超大型长江大跨越输电塔线体系抗震性能分析

2022-11-07王章轩黄士君舒赣平罗柯镕宁帅朋

西安建筑科技大学学报（自然科学版） 2022年4期

陈兵，余亮，王章轩，黄士君，舒赣平，罗柯镕，宁帅朋

(1.国网江苏省电力有限公司建设分公司，江苏南京 210011；2.中国能源建设集团江苏省电力设计院有限公司江苏南京 211102；3.东南大学土木工程学院，江苏南京 211189)

电力系统作为国家的生命线工程，在人民的日常生活中起着举足轻重的作用，其重要性不言而喻，而我国位于世界两大地震带之间，受板块运动的影响，地震活动频率较高，大小规模地震时有发生[1].大跨越输电塔作为电力系统中的重要一环，一旦遭遇地震作用而失效或者损坏，往往将导致局部整个供电系统瘫痪.因此，地震作用下大跨越输电塔的安全问题将变得十分重要，国内外学者对此也开展了大量的研究.

Sun等[2]对多点激励下塔线系统的抗震性能进行了分析，结果表明大跨度塔架结构应考虑多点激励的影响，否则会导致结果失真.Tian等[3-5]通过试验和数值模拟的方法对大跨越输电塔线体系在地震作用下的易损性，倒塌破坏开展了一系列研究.Park H S等[6]通过对高压输电塔进行一系列地震动时程分析，并采用极大似然估计法得出了输电塔的易损性曲线.Albayrak U等[7]基于土耳其典型154 kV输电塔进行了抗震性能的评估，结果表明地震作用下输电塔顶部钢构件更易发生屈曲.李宏男等[8]确定了输电塔体系纵向振动时考虑导线影响的界限，并提出了考虑导线影响的输电塔体系简化抗震计算方法.沈国辉等[9]针对某大跨越输电塔线体系，采用振型分解反应谱法和时程分析法进行了考虑三向输入的地震响应研究.熊铁华等[10]对大跨越钢管混凝土单塔及塔线体系进行了地震响应分析，结果表明：由于输电线的减振作用，塔线模型的底部剪力和一些单元的应力比单塔模型有所减小.田利等[11-13]对输电塔线体系在多维多点下的地震响应以及连续性倒塌问题进行了数值模拟分析；陈龙强等[14]对国外某大跨越输电塔线体系进行了地震时程响应研究，结果表明：塔线体系的顺导线方向是结构抗震更为不利的作用方向.从上述研究可以发现，目前，对于钢管混凝土复合构件型跨越塔抗震性能研究较少，同时，由于塔线耦合效应单塔及塔线体系在地震作用下响应有所不同，且大跨越输电塔线体系往往跨度较大，使得地震动的输入也成为了重要影响因素.因此，本文为充分解析和掌握钢管混凝土型跨越塔在地震作用特别是罕遇地震作用下的响应特征，基于结构分析软件SAP2000分别对单塔进行了静力弹性分析(反应谱分析)、静力弹塑性(Pushover)分析及动力弹塑性分析，并对塔线体系进行了一致激励及考虑视波速影响的非一致激励分析，以期为实际工程跨越塔的抗震容灾能力提供一定的参考建议.

1 跨越塔结构模型

1.1 工程概况

以在建500 kV江苏凤城至梅里超大长江大跨越工程为背景，该工程采用“耐-直-直-耐”跨越方式，耐张段长度共4 055 m，档距分布755 m-2 550 m-750 m，跨越塔全高385 m，建成后杆塔高度将位居世界第一，整体效果如图1所示.

跨越塔由底部至顶部主管规格为Ø2 100×28、Ø2 050×28、Ø1 950×26、Ø1 900×26、Ø1 800×26、Ø1 750×26、Ø1 650×24、Ø1 650×36、Ø1 580×34、1 530×32、Ø1 400×30、Ø1 400×28、Ø1 300×26、Ø1 250×26、Ø1 150×24、Ø1 050×22、Ø11 010×22、Ø914×20、Ø813×18、Ø762×16、Ø660×16，塔身斜管规格在Ø1 020×20～Ø356×7之间，水平管规格在Ø711×14～Ø377×8之间；塔头部分连杆采用等边角钢建造，其尺寸分别为L90×7，L110×7，L125×10，L160×10，L160×12，L180×12，各杆件类型累计91种，钢材牌号为Q345，Q420两种.其中，跨越塔塔身197 m以下主材采用钢管混凝土组合柱，混凝土强度等级为C50，塔身117 m以下主材同时内配环状钢骨加劲件，跨越塔结构中心安装有井筒型电梯，横担-主材连接处采用G20Mn5QT铸钢节点，工程所在区域抗震设防烈度为7°(0.15 g)，场地类别取IV类，设计地震分组为第一组，特征周期Tg=0.65 s.

1.2 计算模型

跨越塔模型基于以下简化和假设：对于主材，采用拟钢理论对塔身197 m以下钢管混凝土柱进行等效；对于节点板等附属构件采用质量放大系数考虑其对主体结构的影响；对铸钢节点采用添加质量点的形式进行加荷.

绝缘子类型为550 kN盘型悬式绝缘子，长度为8.64 m，单联重量为806.4 kg，共六联，弹性模量取为118 GPa[15].

输电线导线单位重量为3 636.5 kg/km，综合拉断力为680 400 N，弹性模量为103 810 MPa；输电线地线单位重量为2 532 kg/km，综合拉断力为537 700 N，弹性模量为170 100 MPa.

在SAP2000中，对于跨越塔、绝缘子及输电线均采用框架梁单元进行模拟，输电线截面模量属性修正为初始模量的0.01倍，采用降温法对输电线施加预拉力.有限元模型见图2、图3所示.

2 反应谱分析

2.1 模态分析

大跨越输电塔线体系作为一种复杂的空间耦联体系，动力特性分析是准确评估其地震响应的重要前提.图4、图5分别给出了输电单塔及塔线体系中输电塔的主要振型.

从下图可知，对于单塔，前三阶振型分别为X向弯曲、Y向弯曲以及扭转振型，且X向与Y向自振频率十分接近，主要由于输电塔主体结构基本呈对称正方形型式，仅在塔头部分质量和刚度略有变化.相比于单塔结构，塔线体系对应自振频率分别减少了5.38%，4.28%，5.37%，即整体而言塔线体系自振频率均小于单塔，原因是塔线体系由于输电线为柔性结构，其对整个体系质量贡献大于刚度贡献.

此外为对比分析主材型式即混凝土灌注区高度对结构动力特性的影响，表1列出了不同模型的振型及自振频率.

表1 振型及自振频率统计表

从上表可以看出，相比于单塔A，单塔B及单塔C主材在灌注混凝土后增大了塔身整体的刚度和重量，且刚度贡献大于质量贡献，使得自振频率变大；但输电塔自振频率并没有随着混凝土浇筑高度的变化呈明显的变化规律，受质量和刚度的双重影响，单塔B自振频率最大.

2.2 位移响应

我国《电力设施抗震设计规范》[16]及《建筑抗震设计规范》[17]中抗震计算均以反应谱理论为基础，下面分别对单塔A、单塔B及单塔C进行X向、Y向7°罕遇地震下的反应谱分析.图6给出了主材角点位移平均值随高度的变化图，表2给出了各模型主材顶点的位移.

表2 模型主材顶点位移

从图6及表2可以看出，模型各自在X和Y方向无论是位移随高度变化趋势还是顶部位移都基本保持一致，原因是三种模型分别在X向和Y向自振频率及振型各自都相近；实际工程模型单塔B其位移随高度的变化趋势在0～197 m呈“下大上小”的趋势，在197 m高度往上呈“下小上大”的变化趋势，原因是197 m高度内为混凝土灌注区域，混凝土的灌注改变了结构刚度和质量的分布规律导致主材下部变形较小，而未灌注的区域变形明显；单塔A位移随高度急剧变大，在0～197 m范围内位移小于模型B，但在197 m后位移不断增大，最终顶点位移与模型B基本一致；模型C为主材全高浇筑混凝土模型，在约117 m高度范围内变化规律与模型B类似，但往后位移同样不断增大，最终顶点位移比模型B减小13.89%.

2.3 应力比

图7给出了各单塔模型在X、Y方向地震作用下的应力比.从图中可以发现，三种模型在地震作用下应力比都处于较低水平，有较大的安全冗余度，且在地震作用Ex及Ey下杆件应力分布基本保持一致；单塔模型A结构最柔，所受地震作用力最小，最大应力比不超过0.4，应力最大点为主材位置；单塔模型B和单塔模型C杆件应力分布类似，模型B最大应力比为0.68，模型C最大应力比为0.66，最大应力点都为斜材处，如图8所示.可见，混凝土的浇筑高度变化不仅改变了跨越塔的最大应力比，同时也改变了最大应力点位置.

2.4 基底剪力

表3列出了不同模型地震作用下的基底剪力值，可以发现：模型在X向和Y向地震作用下基底剪力基本接近；纯钢管单塔模型A底部剪力最小，相比单塔模型B减小了约60%；模型C基底剪力较单塔B稍大，但相差并不明显.

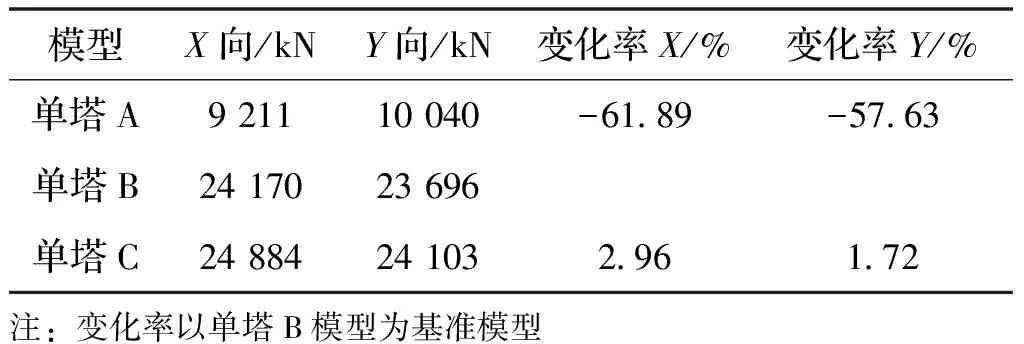
表3 模型基底剪力

3 静力弹塑性分析

3.1 基本原理

静力弹塑性分析(Pushover)是指对结构分析模型施加某种形式的侧向力来模拟地震水平惯性力，然后逐步增大侧向荷载强度，使结构从弹性阶段进入弹塑性阶段，直至结构达到目标位移为止.该过程可以考虑结构在给定地震作用下的非线性行为，明确结构中的薄弱部位，因此可对跨越单塔(工程模型B)进行Pushover分析，检查和评估其抗震性能.具体分析流程如图9所示.

3.2 侧向加载模式

侧向荷载的分布模式代表了地震惯性力的分布，因此侧向荷载模式是Pushover分析的一个关键问题，典型的加载模式包括均布加载、倒三角加载和振型加载模式等[19].本文采用振型加载模式对单塔进行推覆.

3.3 性能点求解

单塔在7度罕遇地震作用下两个方向的基底剪力-顶点位移曲线及能力谱、需求谱如图10、11所示，需求谱与能力谱的交点即罕遇地震作用下结构的性能点，指标如表3所示.从中可以看出，即使在罕遇地震作用下，结构也整体基本处于弹性阶段，并没有塑性铰产生，此时各杆件均处于应力水平较低层次，如图12所示.

表3 性能点指标统计

为判定和识别输电塔薄弱层位置，对其继续推覆直至出现塑性铰，塑性铰发展过程如13、14所示.从图中可以发现，最先出现塑性铰的位置是斜材，此时对应13(a)状态基底剪力为39 981 kN，顶点位移2.099 m，对应14(a)状态基底剪力为39 526 kN，顶点位移1.990 m.随着推覆位移不断增大，斜材出现塑性铰的地方愈发变多，而主材未出现塑性铰，说明在地震作用下相对薄弱层为斜材处，这与反应谱分析中斜材应力比最大的结论是一致的.

4 一致激励动力时程分析

4.1 地震波选取

地震波的三要素分别为频谱特性、有效峰值和持续时间.选波时频谱特性可通过场地类别及设计地震分组确定；有效峰值对应地震动强度，本文将其调整至7°(0.15 g)罕遇地震310 cm/s2；地震持时一般为结构基本周期的5～10倍，本文取为30 s.本文地震波选取三条，两条天然波LYTLECR_WTW115波及ELALAMO_ELC180波，分别记为N1波及N2波，一条人工波记为R波.

地震波时程曲线及与规范谱对比如图15～18所示，表4列出了时程分析计算基底剪力与反应谱计算剪力对比情况.从图18可以看出，三条地震波与规范谱地震影响系数变化趋势基本一致，从表4可以看出每条地震波计算基底剪力及平均值均满足规范[17]要求，表明地震波选取合理.

表4 模型基底剪力对比

4.2 位移及加速度响应

以N1波为例，图19列出了单塔及塔线体系顶底的位移和加速度时程曲线，限于篇幅N2波及R波结果曲线不列出，表5则列出了位移及加速度的具体数值.从图中可以看出，塔线体系无论在X向还是Y向与单塔的时程曲线波形基本相似，变化趋势一致；从图19(b)中可以发现，由于塔线耦合效应，导地线在顺导线方向的来回振动使得南北跨越塔位移时程相差了两倍的初值位移，南北跨越塔呈反向运动，从位移云图20也可看出南北跨越塔运动方向相反；从表5可以看出：三种地震波下，塔线体系位移普遍大于单塔，加速度响应则小于单塔结构；时程分析塔顶位移计算值均略小于反应谱计算值，可比性较好，表明模型合理.

表5 顶点位移及加速度值

4.3 杆件轴力

塔线体系在地震作用下最不利杆件同样为斜材，因此以斜材为特征杆件，对比杆件轴力变化.从表6中可以看出，在N1波及N2波地震作用下，杆件轴力均大于单塔模型，最大增幅在11%左右，R波下杆件内力略小于单塔模型，平均而言塔线体系轴力大于单塔，表明地震作用下考虑塔线耦合体系的整体结构响应是有必要的.

表6 顶点位移及加速度值

5 非一致激励动力时程分析

5.1 基本原理

地震时地面运动是一个复杂的时间-空间过程，不仅具有时变性，而且还具有空间效应，具体体现在行波效应、局部相干效应、场地效应等[20].由于本工程大跨越塔线体系在顺导线方向跨度较大，因此有必要在该方向进行地震动的多点输入.本节基于位移法分析多点激励下考虑行波效应的地震动影响，由于IV类场地等效剪切波速最高值为150 m/s，因此，视波速取为100 m/s，150 m/s及200 m/s，定义γ为行波效应影响系数，如下式所示.

(1)

5.2 位移及加速度响应

表7列出了多点输入下结构的响应及γ计算值.从中可以看出，随着视波速的增大，γ计算值并没有呈现出明显的规律；对于位移响应，南跨越塔γ-uy计算平均值分别为1.076、1.199及1.579，均起到了放大作用，而北跨越塔为0.707、0.907、1.974，除人工波R波外，均起到了减小作用；对于加速度响应，南北跨越塔γ-ay计算平均值在0.727～1.14之间.总体而言，受视波速及地震波的影响，γ值并未呈现明显的规律，本算例中γ-uy最大为2.059，γ-ay最大为1.328，行波效应对结构位移及加速度响应影响较大.

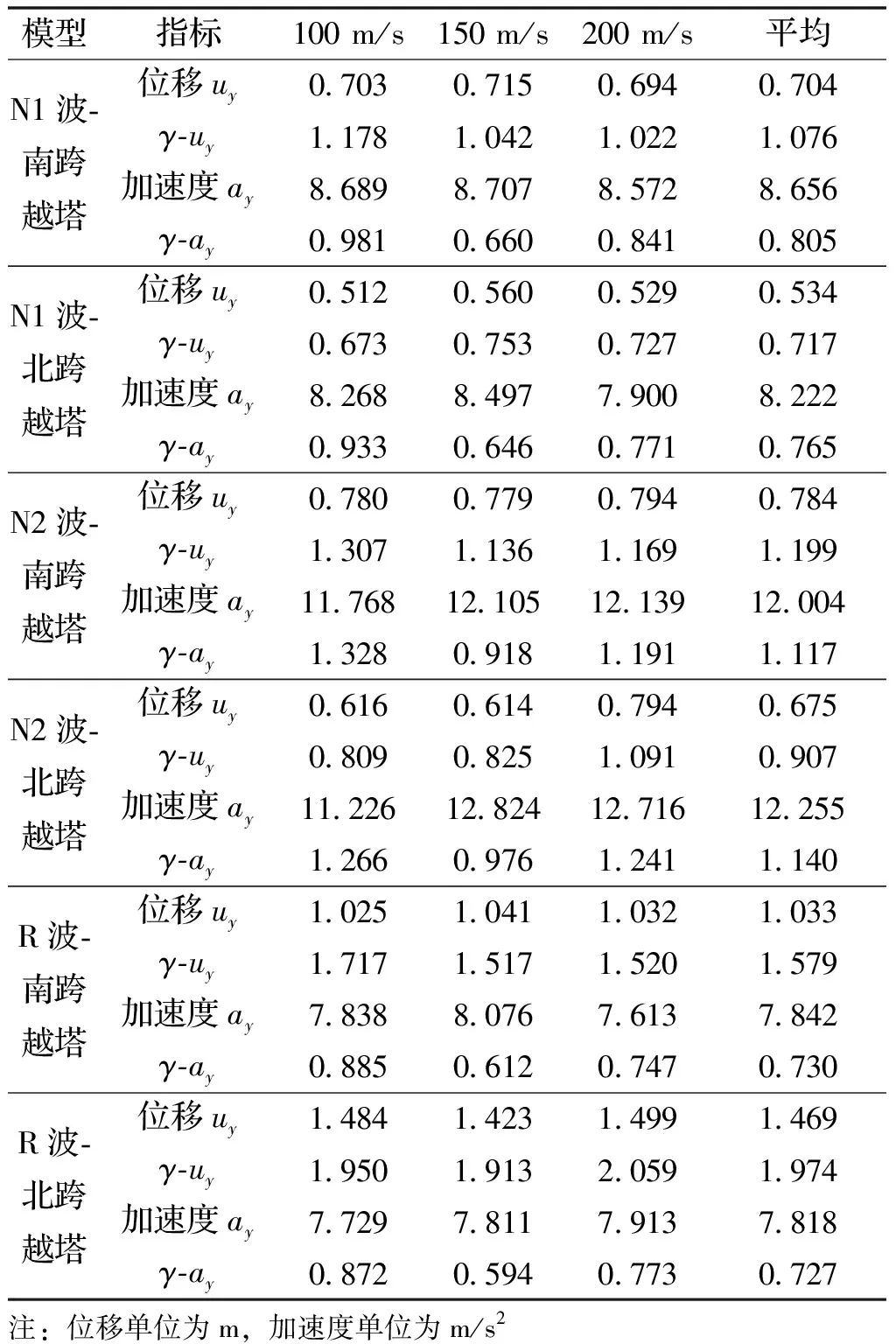
表7 不同视波速下位移及加速度响应对比

5.3 杆件轴力

表8列出了多点输入下斜材的轴力值及γ-Fy计算值，从中可以看出，除个别情况，视波速在100 m/s时γ-Fy最大，在视波速150 m/s时γ-Fy最小，不同地震波下γ-Fy均值位于0.784～1.207之间，本算例中γ-Fy最大值为1.558，可见是否考虑行波效应对杆件轴力有着重要影响，设计中应以予考虑.