飞机防滑刹车控制技术研究综述综述

焦宗夏，白宁，刘晓超，李珏菲，王壮壮，孙栋， 齐鹏远，尚耀星

1. 北京航空航天大学 自动化科学与电气工程学院，北京 100191 2. 北京航空航天大学 飞行器控制一体化技术国家级重点实验室，北京 100191 3. 北京航空航天大学 前沿科学技术创新研究院，北京 100191 4. 北京航空航天大学 宁波创新研究院，宁波 315800 5. 北京控制工程研究所，北京 100190

现代航空工业经过半个多世纪的发展，使得军、民用飞机的安全性得到了提高[1]。但是，除传统航空业所着重关注的空中安全外，飞机在地面阶段的安全性问题仍不容忽视，尤其在起飞前和着陆后的事故量已超过其飞行阶段[2]。现代大型飞机所具备的减速手段主要包括机轮刹车、引擎反推[3]、减速板制动和减速伞制动[4]等。但是，引擎反推、减速板和减速伞的使用效果在飞机单次降落过程中均会随风速和机速的变化存在不确定性，无法在飞机降落的全速度范围下提供可靠的制动力。因此机轮刹车系统是保障飞机顺利着陆最基本的系统，在飞机研制过程中与飞行控制系统在安全性上具有同等要求，被国际标准定为安全等级要求最高的 A 类子系统之一。另外，当前世界各国致力于发展高速飞机，对机轮刹车的能力提出了更高的需求。

飞机防滑刹车控制技术是实现高效机轮刹车的核心。世界上第一款飞机刹车系统由法国 Automobile 公司于 1929 年设计制造，该系统通过纯机械方式完成了飞机速度与轮速的比较，利用比较结果触发防滑机制。到了 20 世纪 50 年代英国 Dunlop 公司也基于机速与轮速的差速比较原理开发出了类似的 Maxaret 飞机防滑刹车系统[5]，同时期美国 Hydro-Aire 公司(后整合为 Crane 公司)于 1947 年为 B-47 飞机开发了现代意义上第一款飞机防滑刹车系统。它以惯性传感器为测量元件，通过机械机构推动微动门，利用开关式信号控制电磁阀实现机轮防滑，并命名为 Mark I 型系统。随后该系统逐步应用于 B-52、F-100 以及 B707-100 等商业客机[6]。伴随传感器及电子技术的发展，Mark II 型系统上首次引入了轮速传感器，通过模拟电路实现了刹车压力偏置调节，实现了刹车效率的有效提升，并装备于 C-130A 等飞机。为了进一步提高飞机在不同跑道的刹车效果，Mark III 型系统引入自适应机制，显著提升了飞机在湿滑跑道的刹车能力，装备于 F-15、F-18 以及 B-1 等美国在役机型。伴随微电子技术的发展，Mark IV 型系统是第一个以数字控制器为载体的飞机防滑刹车控制系统，通过进一步改进算法使得飞机在所有工作条件下刹车效率均大于95%，被应用于 F-16、C-17、C-130 J 以及Boeing系列的737、747、757、767、777等商用客机[7-8]。最新的 Mark V 型是一种电传刹车(Brake-by-Wire)系统，装备于Airbus的 A400M、Boeing的787、美国联合攻击战斗机(Joint Strike Fighter, JSF)、可重复使用空间飞行器 X-33、X-34 等演示样机上。美国 Crane 公司目前作为飞机刹车防滑刹车系统的引领者，占据了国际上 65% 的商业市场以及西方 80% 以上的军事市场。另外，还有 Goodrich、Safran 和 Meggitt 等公司[9]也开发飞机防滑控制产品，主要服务于欧洲飞机制造商[10]。

飞机刹车的基本原理是通过控制刹车力矩调整机轮与地面的滑移状态进而使得地面的摩擦力(结合力)矩与刹车力矩近似平衡。但是，机轮与跑道间独特的非线性关系使地面的结合力受道路条件、机轮速度、飞机速度、轮载、胎面温度[11]等多方面因素影响，尤其在刹车过程中速度跨度较大，机轮载荷在升力作用下的变化达到20%以上[12]，致使同样的路况可能在不同的载荷条件下产生不同的结合力矩。而且，多数飞机刹车系统可用于实时控制的传感器只有轮速和刹车压力[13]，无法实现对刹车力矩的可靠闭环，刹车盘的摩擦系数在自身材料、速度、湿度和温度等耦合因素影响下波动可能达到50%以上[14]。

另外，全天候飞机的刹车系统要求在不同着陆条件和整个着陆速度内均具有一致性，即飞机刹车系统应具备在可能遇到的所有着陆条件下(正常的机体着陆配置[15]、不同机速、不同阵风和不同道路条件)、在有限跑道长度内、经过相似的刹车过程后使飞机平稳、可靠刹停的能力。但是，不确定着陆方式及可能存在的阵风干扰更是进一步突出了地面结合力矩和刹车力矩的非线性影响，使得飞机在地面滑跑时非常容易出现机轮抱死，尤其在高速状态下一旦抱死 300 ms 即可能引起爆胎[16]。上述问题不仅对飞机刹车系统硬件的快速性和灵敏性提出了较高的要求，更使得控制律在设计时需要着重平衡刹车能力的极致利用与不同着陆条件下控制稳定性的关系。

飞机防滑刹车控制关注的主要问题是如何通过控制刹车力矩实现地面结合力的可控利用。虽然国内外防滑刹车控制在学术上基本涵盖了所有主流的控制方法，诸如非线性自适应控制[17-18]、滑模控制(Sliding Mode Control, SMC)[19]、模型预测控制(Model Predictive Control, MPC)、模糊控制、人工神经网络(Artificial Neural Network, ANN)和智能学习控制[20]等，但其中多数算法仅在少数仿真工况中进行验证，缺乏更多惯性台和飞行着陆试验，无法确定它们在各种不确定性因素共同作用下的鲁棒性。

第1节从典型的飞机刹车系统出发，按硬件组成划分依次介绍了液压刹车、电刹车、应急刹车和自馈能刹车。第2节从应用需求角度归纳了关键评价指标。第3节用数学模型的方式表述了系统中的典型非线性环节，主要包括轮胎-地面摩擦、刹车盘压力-力矩特性、起落架以及机体在着陆环境下受到的非线性扰动。第4节按照历史上典型防滑刹车控制系统的划分，着重阐述和讨论了在不同阶段具有代表性的防滑控制方法。第5节介绍了刹车控制律全数字仿真与试验方法。第6节根据当前研究中所存在的问题和技术发展趋势对未来防滑刹车控制研究重点进行了展望。

1 飞机刹车系统架构

介绍4种典型的飞机刹车系统架构：传统飞机大量装备的液压刹车系统和新式飞机选装的全电刹车系统(框架结构如图1所示)，用于常规刹车系统故障失效后的应急刹车系统以及可独立于机载动力源工作的自馈能刹车系统。

1.1 液压刹车系统

传统的液压刹车系统主要由脚蹬指令传感器、轮速传感器、刹车控制盒、减压阀、液压电磁阀、防滑刹车控制阀、刹车作动器与刹车盘构成的刹车装置以及其他液压附件构成。脚蹬踏板采集飞行员刹车指令，刹车控制器以轮速信号为反馈，根据刹车指令调节供给刹车作动器的油液压力，液压作动器受刹车压力作用推动刹车装置内的动、静盘贴合产生刹车力矩。

防滑刹车控制阀作为飞机刹车系统的核心元件，其性能是高效防滑刹车的基础。在 Mark I 系统时代，开关电磁阀作为主要控制单元，仅能配合简单的控制逻辑实现基本的防滑功能；随着液压控制元件的发展，到 Mark II 系统时期已经由具有一定压力调节能力的比例阀执行防滑操作，使得压力控制更准确，有效降低了轮胎因深打滑而造成的磨损。而 Mark III 系统中，随着具有高频响应的电液压力伺服阀的应用，将飞机防滑刹车能力提升到了新的高度，也为恶劣跑道条件下的防滑刹车提供了必要的硬件基础。直至今日，国内外众多机型如 B737、B747、B777、F-16、F-22 等仍依赖于电液压力伺服阀进行防滑刹车控制。

但是飞机刹车系统中广泛装备的喷嘴挡板式压力伺服阀[21]也在长期应用中暴露了该结构抗污染能力差、故障率较高的弊端，甚至在某型飞机刹车系统中，伺服阀的故障率占到全系统的40%以上[22]。其原因在于刹车作动器内的死腔结构，使得刹车时油液受高温影响而发生炭化后很容易堵塞阀喷嘴，进而造成伺服阀性能下降甚至损坏。为此，有必要选择其他液压阀实现传统喷嘴挡板式压力伺服阀的原位替换。

直接驱动伺服阀(Direct Drive Valve, DDV)[23]不仅从结构上用直线力马达代替了喷嘴挡板前置级，在减少内漏的同时提高了油液的抗污染能力，还用位置电反馈取代了过去的机械反馈，有效减小了阀的滞环特性，并且具备了关于阀芯位置状态检测的能力[22]。另外，随着数字液压技术[24]的兴起，采用高速开关阀阵列作为刹车阀代替传统压力伺服阀成为一种新的选择。开关阀阵列利用多个高速开关阀来搭建液压半桥，通过不同流量高速开关阀的开闭，模拟伺服阀的不同流量状态，进而配合刹车腔压力传感器和控制器实现压力伺服控制的功能，具有抗污染能力强、响应快的优势，同时多个开关阀的冗余特性有效提高了阀的可靠性。目前，该开关阀阵列已顺利通过地面惯性台验证[25]进入装机试验阶段。

1.2 电刹车系统

出于更高的安全性和易维护性需求，美国国防部和联邦航空管理局(Federal Aviation Administration, FAA)自 20 世纪 70 年代开始探索论证在飞机上用更多的电作动系统替换传统的液压作动系统，最早于 1982 年在 A-10 飞机上测试了电刹车原型样机[26]。而后于 20世纪90 年代在装备电传操作系统和改进版 Mark V 防滑系统的 F-16 飞机上成功测试了由 MDC、Goodrich 和 Crane 等多家企业联合研制的新型电刹车系统[27]。该系统在硬件架构上由驱动器、电机、包含减速器与滚珠丝杠的机电作动器(Electro-mechanical Actuator, EMA)代替了伺服阀、液压缸等液压组件。刹车控制盒给出指令后经 EMA 控制器输出脉宽调制(Pulse Width Modulation, PWM)信号控制电机，利用电机驱动减速器来完成对滚珠丝杠的位置、速度及刹车力的控制。21世纪后，法国 Safran、美国 UTC 公司进一步将电刹车技术应用于 B787 等民用客机，这也标志着电刹车技术日趋成熟，其可靠性和安全性已达到适航标准[28]。

全电刹车系统主要为多电飞机服务，不仅方便进行能量管理，同时作为最新的产品配备了更多反馈信号用于改善刹车力矩和防滑性能；更快的数字运算单元可以在更短的控制周期内实现复杂的防滑控制算法。另外，作为电气系统，其发生故障时方便检修、易于维护，避免了液压系统中存在的油液污染、泄漏和腐蚀问题。而液压刹车的结构相比电刹车更为简单，技术成熟，具有故障元件少、稳态误差小、鲁棒性强等优势。

国内在此方面虽然起步较晚，但在西安航空制动科技有限公司、北京航空航天大学、西北工业大学、南京航空航天大学和中南大学等众多校企合作下已有多款电刹车系统完成了飞机试飞着陆验证[29]，标志着中国也已掌握了具有独立自主知识产权的电刹车系统及防滑控制技术。另外，在电驱动刹车系统架构上还有学者提出使用泵控和阀控相结合的电静液刹车系统方案[30]，一定程度上减少了对机载集中液压源的依赖，提高了安全性。

1.3 应急刹车系统

应急刹车系统是为保证飞机常规刹车系统失效后仍具有刹车能力的关键系统。辅助气瓶是一种常用于轻型飞机的应急手段，它通过独立的管路作用于梭阀，以取代液压流体产生刹车压力。鉴于其有限的制动能力，美国军方在 B-1 和 F-16 上使用与常规液压刹车系统在物理上完全隔绝的液压源为其供能[31]。而民用飞机上则利用蓄压器，通过机械钢索或电控信号控制刹车阀实现应急刹车[32]。

1.4 自馈能刹车系统

北京航空航天大学的焦宗夏团队近年来提出一种“无源刹车”架构[33]，如图2 所示。该架构将小型液压泵通过传动装置连接到机轮旋转部分，当飞机在地面滑跑时，机轮通过传动机构带动泵旋转，形成具有一定压力和流量的液压源，然后通过高速数字开关阀组调节到适当的压力，供给刹车作动器[34]。该结构不仅省去了机上集中油源至主轮刹车系统的液压管路，还提高了油液的抗污染能力，可以在不依赖于机载动力的情况下实现刹车，有效提高了飞机着陆的安全性。

2 刹车控制指标

合理的评价指标是充分反映飞机在着陆时具备相应能力的量化标准，它是从不同角度评价着陆性能、判断其实际应用价值的准则。不同类型的指标应尽可能覆盖飞机着陆刹车时可能遇到的所有工况。在此，结合飞机适航认证[35]与汽车刹车行业的相关标准[36]提供一些具有参考价值的指标，以方便研究人员对不同刹车算法的优劣进行比较。

2.1 刹车效率

刹车效率η用于表征飞机通过刹车利用地面最大摩擦系数的能力，它是在适航要求中确定湿滑跑道加速-停止距离的必要系数，也是验证刹车控制算法的核心指标。由于在实际条件中难以获得实时最大结合系数，为此民用飞机在设计与试飞验证中常用的效率计算包括压力效率法、力矩效率法和滑移率效率法[35-37]。

压力效率法是外场试验评估和计算刹车效率最常用的方法[35]。它是在首末两次打滑期间，由刹车压力极大值点连线所构成的理想压力包络线与实际压力曲线在时间域或刹车速度范围内的面积比来确定(图3)，其计算方式为

(1)

式中：ηpre为压力效率；A和AI分别为实际和理想压力与横轴所围的面积，同理也可用刹车扭矩来表示。

力矩效率法是比较瞬时地面结合力Fadh实际耗散能量与制动距离内瞬时结合力峰值Fap连线的积分[35](图4)，其计算方法为

(2)

(3)

式中：ηT为力矩效率；Pb为刹车压力；J为机轮转动惯量；rw为机轮半径；Vw为机轮速度；s为刹车距离；f(·)为刹车压力至刹车力矩的映射关系。

滑移率效率法需要先通过机轮瞬时滑移率λ与最优滑移率λ*计算得到瞬时效率ηins，然后用瞬时效率对距离积分，其计算公式为

(4)

(5)

(6)

式中：ηs为总滑移率效率；Vp为飞机速度。图5所示为通过瞬时地面结合力获得最优滑移率的方法。

上述3种效率计算方法主要用于处理在未知地面最优摩擦系数时，通过最大刹车压力和估计的地面结合力峰值来确定最优状态。而仿真条件下，由于刹车环境的最大摩擦系数可以人为设定，也可以仿照压力效率法的方式用地面最大摩擦系数与实际摩擦系数和横坐标(时间或速度)之间的面积比来表示刹车效率。

2.2 平均减速率

(7)

式中：td为上述速度段所经过的时间。

2.3 刹车距离

刹车距离db用于表征飞机刹车过程中的整体性能，通过记录飞行员第一次踩下刹车踏板的时间t0与达到防滑失效速度的时刻tn，进而对速度积分：

(8)

2.4 打滑轮速最大降比

出于对防滑的快速性需求，通过计算机轮打滑过程的理想轮速ωide与最低轮速ωslipmin的下降比，综合判断控制律的防滑水平与作动器的瞬态性能。图6表征了机轮打滑过程中获得ωide和ωslipmin的方式。打滑轮速最大降比ωdmax的表达式为

(9)

2.5 防滑最大偏航率

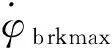
(10)

2.6 俯仰波动

飞机着陆时的俯仰主要与刹车造成的机体负载转移有关，当机体剧烈振动或俯仰过大时会降低飞行员操作水平，带来安全隐患。尤其对于轻小型飞机而言，强烈的振动甚至会导致飞行员难以准确目视仪表。从人员安全与舒适程度出发，刹车过程应尽可能保证飞机俯仰平稳，选择在刹车过程中机体俯仰角αosc的累计俯仰波动Sacc作为评价指标：

(11)

3 刹车系统模型与环境

数学模型是描述飞机刹车过程中物理学现象的直观方法。合适的数学模型是研究飞机防滑刹车问题的基础，也是完成全数字仿真试验的关键。本节将从轮胎-地面摩擦、刹车盘压力-力矩、起落架振动与机体在着陆时所受到的环境干扰出发，以模型的形式描述飞机刹车过程中的非线性特征。

3.1 轮胎-地面摩擦模型

机轮是飞机在着陆滑跑阶段与道路接触的唯一单元，其特性对飞机刹车过程中的动态行为起到至关重要的作用。与汽车轮胎相比，虽然其结构和形状相似，但飞机速度更快、载荷更大(美国 Boeing 777-200 ER 典型着陆重量为 190 t，着陆速度 70 m/s)。在飞机着陆刹车过程中需要防滑控制律在更宽的范围内适应其非线性特征。当前，关于轮胎模型的研究已经积累了相当丰富的成果，从基于物理意义的机理模型，到结合试验数据拟合的经验/半经验模型，以及可以精确描述轮胎与地面接触区域相互作用的有限元模型。

虽然有限元方法可以大幅提高模型精度[38]，但是其高昂的计算成本使其难以直接应用于防滑控制律设计和整机着陆仿真环境的搭建[39]。机理模型通常以适用于轮胎材料和结构的物理原理为基础，其中每一个参数都有准确的物理意义。典型的机理模型有 Brush 模型[40-42]、Lacombe 模型[43](梁模型)和 Mancuso 模型[44]，以及在 Brush 模型基础上扩展的 Sakai 模型[45-46]和3种HSRI-NBS 模型[46-47]等。纯机理模型的假设各异，与现实情况存在一定差距，导致其难以充分适应试验结果。经验模型是实测数据通过回归方法对特定的公式结构进行经验参数的插值拟合，而半经验模型是由轮胎运动过程中的物理参数结合试验数据趋势及经验参数所构成。两者的差异在于经验模型中的参数一般不具有物理意义，也不表征轮胎结构的任何特征。而半经验模型中通常会引入一些理论作为模型中变量间的约束，如摩擦椭圆理论[48]、最大化摩擦耗散原理[49]等，更多关于半经验轮胎模型可参考文献[50-51]等。

在经验/半经验模型中最常见的是用机轮滑移率λ与纵向滑移系数μ的代数函数表征轮胎与摩擦的非线性关系。两种经典模型分别为 Burckhard[50]和魔术公式(Magic Formula, MF)[52]模型。Burckhard 模型是基于指数函数的经验模型，该模型在指数函数的基础上进行建模，鉴于指数函数求导的优越性，Burckhard 模型被广泛应用于道面识别中。作为工业上应用最成熟且广受工程师青睐的 MF 模型是基于三角函数的经验模型，与实测数据具有较高的拟合度[53-54]，常用于建立仿真环境。该模型从诞生之初至今经过不断扩展和完善，其公式和参数集已经形成了一个涵盖多种轮胎，全面描述轮胎纵向和侧向摩擦力的商业软件[55](图7所示为 MF 模型所表征的典型纵向μ-λ关系)，鉴于它与试验数据的高度一致性，也常用于验证其他轮胎模型。

在飞机着陆过程中，机轮与跑道相互作用时摩擦系数并不完全沿着图7的μ-λ曲线趋势变化，还存在“跳跃”、滞回等现象[56-57]。为进一步开发轮胎的极限性能，保证刹车系统在工作时的稳定性，更多因素被考虑加入模型[58]。LuGre 纵向摩擦模型[59]是在 Dahl 模型[60-61]的基础上对库仑摩擦项进行修正，以紧凑的形式捕捉了机轮的瞬态效应。典型的 LuGre 模型有集中式[59]、分布式[62]和准稳态式[63]。集中式是基于点接触假设的动态模型；分布式是基于面接触假设的模型，进一步细化接触面内载荷变化和滑移状态分布对摩擦力的影响；准稳态式则是基于分布式的模型，可推得典型的μ-λ关系，方便与 MF 模型进行对比。此外，还有更多学者将 LuGre 模型推广到二维[49]以及更多的参数形式[64]。

根据 LuGre 模型及道路试验[65]可知，当滑移速度改变时，即使在同一路况条件下μ-λ曲线也会发生变化，为方便与 MF 模型进行比较，图8所示为 LuGre 准稳态模型下不同机速Vp的μ-λ关系，随着飞机速度的降低，最大摩擦系数和最优滑移率都在变大。该模型有助于指导控制律适应不同机速下最优滑移状态变化的设计。

3.2 刹车装置压力-力矩模型

飞机刹车装置包括液压作动活塞、刹车静盘、刹车动盘及其他附属部件。在飞机主轮触地后，动盘随机轮一起转动，静盘则与轮毂固连不发生转动。在进行机轮刹车时，依靠动盘和静盘互相压紧而产生刹车力矩，其结构如图9所示[66-67]。动盘和静盘的压力是由作动器传递产生，为此刹车装置主要实现从刹车压力至刹车力矩的转换。刹车盘摩擦系数与刹车装置作动系统的动态响应对生成具有非线性特性的刹车力矩起到重要作用。

首先，关于刹车盘的摩擦系数多数仿真环境仅简化为常数处理[67]，即通过常值增益系数实现刹车压力至刹车力矩的转换。实际上在刹车过程中，刹车盘摩擦系数不仅随速度、温度变化，当发生不同程度振动时也会诱导其摩擦力矩发生改变[68-69]，图10所示为由于刹车盘摩擦系数变化而导致的刹车盘压力/力矩系数kb在一次刹车试验中的变化[70]。目前所公开的资料仅对其在材料学范畴对该过程产生的原因做了定性分析[71-72]，还没有能完全描述该现象的数学模型。

关于刹车装置的压力-力矩响应特性，美国国家航空航天局(National Aeronautics and Space Administration, NASA)曾研究了3种关于刹车压力-力矩动态响应的典型模型[73]，它将刹车压力-力矩响应的计算分别表征为无阻尼非线性弹簧、带粘性阻尼的线性弹簧以及具有滞后记忆功能的非线性弹簧，采用 DC-9-10 飞机的刹车系统数据与上述3种模型进行对比。试验数据表明具有滞后记忆功能的非线性弹簧模型与真实试验数据更吻合。另外，也有学者通过分析液压刹车系统内回力弹簧的作用及动静盘动作时弹性形变的特征，结合真实机型刹车装置试验数据(图11)得到带死区的滞环模型[74-76]。

该滞环模型可由分段函数表示：

(12)

式中：Tb为刹车力矩；Tbl为上一时刻输出力矩；Pb为刹车压力；Pbl为前时刻输出压力；Pd为死区刹车压力；kpr=Tm/(Pm-Pd)和kpd=Tm/(Pmh-Pd)分别为升压和降压过程的压力-力矩系数；Tm为最大刹车力矩；Pm为最大刹车压力；Pmh为最大迟滞刹车压力。图12所示为该分段函数可以模拟试验数据中刹车压力的滞环特性。

3.3 起落架模型

起落架是飞机在着陆时起支撑作用的关键部件，是传递机体和机轮间动力学关系的通道。当飞机主机轮触地后处于尚未刹车阶段时，机体速度通过起落架传递给机轮轮轴，使机轮速度在极短时间内在地面结合力作用下达到飞机速度的同等水平。同时，在刹车阶段，机轮所受的地面结合力也通过起落架传递至机体以改变飞机运动状态。

起落架结构复杂，力学分析困难，而精确的有限元模型[77]计算成本较高。为此，在防滑控制律研究初期可以仅保留其纵向力学特征，并简化等效为图13 所示的质量-弹簧-阻尼系统[78]：

(13)

式中：FL为单轮载荷；kL和cL分别为起落架等效弹簧胡克系数和阻尼系数；zp为机体在起落架位置的垂向位移。

事实上，飞机在滑跑过程中起落架可能在动态载荷和其他力的作用下产生摆振(Shimmy)和走步(Gear-walk)两种振动现象[79](图14)。其中摆振主要出现在可沿轴转动的前起落架[79]，在此暂不赘述，更多信息见文献[80-81]；走步通常是由主起落架机轮与地面之间变化的结合力引起的低频振动，振动频率通常在6～12 Hz之间[82]。

由于主起落架的走步现象在机轮纵向上产生了一个“虚拟”的滑移量，该值与刹车生成的机轮滑移量耦合在一起，给闭环防滑刹车控制造成了干扰。为此，李波和焦宗夏[83]将起落架支柱等效为等横向抗弯刚度的悬臂梁来描述走步现象。另外还有一种简单的方式是通过一个连接起落架垂直轴的旋转弹簧阻尼系统(图15)来描述防滑刹车控制过程中的起落架走步，则起落架附加自由度动态可表示为[12]

(14)

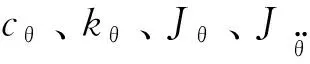
3.4 机体模型及着陆环境

虽然在空中飞机需要考虑6个自由度的运动姿态，但在着陆阶段起落架和地面对机体的自由度形成限制，另外，航向操纵系统会保证飞机在非对称着陆、大侧风等工况下的偏航稳定性。当仅验证控制律对道面适应情况时可以按照如图16所示的简化飞机刹车模型[84]。

机体沿纵向的受力情况为

(15)

式中：M为机体质量；Ffl=μlFNl、Ffr=μrFNr分别为左、右侧主轮地面纵向结合力；μl和μr为左、右侧轮胎与跑道间的摩擦系数，通常μr=μl；FNl和FNr为左、右侧地面支持力；Te=Te0+KvVp为引擎残余推力，其中Vp为机体速度，Te0为其初始值，Kv为发动机推力的衰减系数；空气阻力Fa可表示为ρCxSVp2/2，ρ为空气密度，S为飞机的迎风面积，Cx为空气阻力系数。

另外，在飞机刹车过程中由于升力及刹车作用而导致的纵向负载转移效应[85]可表示为

(16)

式中：FNn为前轮所受支持力；Ffn为前轮所受滚动阻力；G为飞机所受重力；H、Lm和Ln分别为飞机重心高度、主轮和前轮至重心的距离；ky为垂向的空气阻力系数。

通过前述分析，在飞机着陆时，仅沿飞机运动方向受到的环境扰动包括跑道条件以及引擎残余推力和阵风所引起的不确定性空气阻力，而在垂直地面方向还包括由于机体负载转移和随速度变化的升力对机轮载荷造成影响。其他更多的单轨模型[86]、三轮车模型[87]等可以增加地面侧向力和侧风扰动，以进一步验证飞机在跑道存在偏航和非对称着陆情况下的刹车控制问题。

4 防滑控制技术

控制方法的设计依赖于系统的硬件结构。电子技术、作动器和传感器技术的发展推动了防滑刹车控制架构的变迁。本节按照飞机防滑刹车控制技术的发展，从技术应用和学术研究两个角度介绍分析了具有代表性的防滑控制方法。

4.1 机械开关式防滑控制

早期的机轮防滑，仅仅作为机轮的附属功能，通过开关型控制减小因机轮打滑而造成的胎面损伤，以延长机轮的使用寿命。在以 Mark I 型刹车系统为代表的早期防滑系统中，当机轮受到刹车力矩作用而减速到一定程度时，通过安装在防滑机轮上的惯性传感器检测机轮的减速率，当超过一定限额时借助机械装置控制液压系统松刹，进而使得机轮恢复转动完成防滑，如图17所示。同时期也有通过惯性传感器触发微动开关利用继电器控制电磁阀实现泄压防滑。究其核心在于判断轮速的变化率是否达到某一特定数值[88]。虽然刹车硬件系统经过多次改进，但从控制的角度来看，机轮轮速的变化率作为一种有效判断机轮打滑状态的控制变量一直沿用至今。

4.2 偏压调制式防滑控制

随着飞机着陆速度的增长，开关式防滑刹车已难以满足民用航空及军事作战时对飞机刹车距离的要求。由于传感器技术的突破，相对准确的车轮速度可以由脉冲计数的轮速传感器所测得，人们开发出了比开关式防滑效率更高的偏压调制防滑控制。所谓的“调制”控制是指刹车压力按照某种机轮滑移状态的变化，以特定的规律进行循环往复的升压和降压。通过不同规则和阈值的设计保证在控制律中不显式使用最优滑移状态值的情况下使机轮滑移状态保持在最优点附近[89]。早期它的设计多是基于启发式阈值和专家经验，而后基于周期轨[90]和混沌原理[91]分析使其在稳定性上获得了理论支持。

Mark II 型防滑刹车系统作为一种调制型控制系统是以机轮减速率为控制变量与阈值进行比较[88](其架构如图18所示)，虽然其控制变量与 Mark I 相同均为机轮减速率，但是通过微分电路获得的机轮减速率比惯性传感器品质更高，并且刹车压力已经由当初的开关式控制调制为类似于三角波控制的缓慢升压、降压控制，使得机轮减速率在目标减速率附近波动。同时期，更多诸如滑水保护、着陆保护以及交叉保护等与机轮防滑的相关辅助功能被纳入到防滑技术研究。

鉴于偏压调制式控制方法出色的应用表现，在飞机和汽车刹车学术领域以现在的刹车系统硬件为平台进一步扩展了调制式防滑刹车算法，即通过选取典型的状态变量，如机轮滑移率、机轮轮速和机轮减速率等，通过判断状态变量在不同时间、不同刹车状态达到不同的阈值而进行控制输出的方法。Lonbani 等[92]基于机轮速度和估计的滑移率值设计了基于四状态切换的防滑刹车控制算法，并进一步探究了作动器延迟和动态带宽对此算法的影响。还有学者利用滑移率与减速率构成状态空间，设计由五状态构成的混合状态控制器[93]，这种方法需要μ-λ有较明显的极值且该极值保持不变才能保证其状态切换的有序性[94]，Gerard 等[89]依据实际条件，从测量噪声与刹车装置驱动延迟的角度对上述混合状态控制器进行了优化，在试验中证明了状态的有序切换形成了稳定的极限环，且与传统的博世防抱死刹车系统(Antilock Braking System, ABS)系统相比具有更高的刹车效率。Tanelli 等[95-96]根据非线性动力学设计了四状态刹车调制控制律，通过系统相平面分析了极限环存在的必要条件，并通过 Poincare 图评估了其渐近稳定性。另外，在调制式刹车控制中状态变量的测量尤为重要，在观测变量与阈值的比较判断中常常将机轮半径作为常数[94]，但是由轮胎松弛动力学及试验数据可知机轮在滚动时的有效半径与标称值不同[97]，估计刹车时机轮的有效滚动半径[98-99]，将使得真实控制过程中的观测变量更符合理论分析。

调制式刹车控制方法在于无需解析轮胎与地面间准确的动力学关系，对传感器和作动器要求低，控制简单易于实现。但是其具有一定容错性的判断阈值既难以充分利用单一道面的极限摩擦力也约束了在不同路面最优滑移状态改变时的控制一致性，难以保证相对稳定的刹车效率。

4.3 自适应防滑控制

随着喷气式飞机在雨雪恶劣条件下使用调制式防滑控制方法时在刹车效率上的局限性，FAA提出了进一步改善防滑系统在湿跑道条件下工作性能的要求。

1) 滑移速度式自适应防滑

Crane 公司发开了第一款称之为具有自适应能力的防滑刹车控制系统，即 Mark III 型防滑刹车系统[88](图19)。较前代而言，在硬件上它用控制响应更快和精度更高的压力伺服阀取代了比例阀，引入了采集精度更高的轮速传感器，在算法层面将传统的机轮减速率替换为由预设飞机减速率生成的参考速度与轮速信号的差(准滑移速度)作为控制变量，有效减小了刹车压力的波动程度，提升了刹车效率[100]。并且在后续的 Mark IV 型刹车系统中依旧承袭了这一控制原理。

如图20所示，该控制律可有效兼容自动刹车功能，通过飞行员扭转选择不同的自动刹车等级(L0、1、2、3、4、HI)，以获得不同的参考减速率[101]。

自适应防滑刹车系统需要在不同跑道条件下将机轮滑移状态控制在最优滑移状态附近较小的范围内[102]。通过在控制律中预先设定参考减速率很难在每次着陆过程中匹配适应不同的着陆条件。中国民航总局曾分析着陆阶段事故多数是由于在恶劣着陆条件下飞行员对跑道状态判断出现错误，同时刹车控制系统也缺乏对跑道条件的有效辨识[103]。由此反映出自适应刹车控制的难点之一在于需要在防滑刹车控制过程中融入对地面摩擦状态的判断。因而有必要开发一种新的自适应防滑刹车控制方式。

2) 主动滑控自适应防滑

北京航空航天大学的焦宗夏团队从飞机着陆过程中不同干扰对刹车控制的影响入手[104]，克服了摩擦盘力矩系数变化和机轮载荷波动的干扰，以经典的跑道-轮胎摩擦特性为基础，在仅使用轮速传感器的情况下开发了一种根据刹车压力判断机轮滑移状态变化的新型自适应防滑刹车控制方法。通过预测地面结合力(摩擦力)梯度变化来判断道路结合能力[70,105]，摆脱了特定轮胎模型的束缚，实现了对不同道路最大结合能力的利用，同时在刹车过程中克服了刹车力矩波动的干扰，实现全程不打滑高效刹车，其控制架构和控制效果如图21和图22[70]所示。该算法成功通过了传统液压刹车系统和电刹车系统的惯性台和真机着陆测试，实现了多种机型的装备应用。

3) 滑移率式自适应防滑

在学术研究领域，为实现机轮刹车的自适应性，主要是从机轮滑移率与地面结合系数所存在直接非线性映射关系入手，通过对最优滑移率的跟踪实现地面最大结合力的利用。整个刹车控制器通常由参考滑移率识别和目标状态跟踪控制构成[106]。

关于参考滑移率的获取可以基于 Dugoff、Burckhard 等轮胎模型采用优化的卡尔曼滤波[107-108]和参数自适应[109]等方法实现模型参数的估计辨识。也可以在未打滑状态，基于静态刷子模型和小滑移区域线性假设[110]通过递归最小二乘法[111]、非线性最小二乘[112-113]等实时估计纵向滑移刚度(Extended Braking Stiffness, XBS)。另外，针对 LuGre 模型，由于刹车过程中轮胎动态远高于飞机动态，可以先假设飞机速度不变[114]，再利用非线性观测器[115-116]或参数自适应[117]实现道面辨识。还可以借助模糊理论[118]或XBS[119]处理辨识前的初始参数问题[120]。

通过道面识别获得目标参考滑移率后，即可通过线性或非线性比例-积分-微分(Proportion-Integration-Differentiation, PID)控制[121-122]、非线性控制[84]、滑模控制[123]、MPC[124]等方法完成对目标滑移率的跟踪。由于传统非线性控制方法对模型的精度要求较高，目前在可查阅的文献中还没有经过飞机着陆试验验证的参数自适应方法可以在不同着陆工况下克服关于道面、轮载[125]和阵风等随机扰动。为此采用非线性控制很难达到自适应防滑刹车的标准。而 MPC 作为一种将控制问题转化为处理在线受约束最优化问题的控制方法，由于其存在动态修正环节，使其在汽车防滑领域实现了工程应用。它在处理防滑问题时，具有兼顾诸如减速率，刹车效率和舒适度等多个优化目标[85]的优势，并且刹车控制作为快响应系统，可以设计专用的求解器[126]或采用显式非线性模型[127]等手段提升实时性。

SMC 是一种对扰动和不确定性具有较强鲁棒性的方法，在飞机刹车和汽车 ABS 中均有一定程度的应用。但是由于实际情况下作动器的迟滞效应以及其他未建模动力学，SMC 可能导致在压力输出伴随高频振荡问题[99]，从而造成控制失稳、意外打滑和刹车盘过度磨损。为此有学者在刹车控制中融入惯性延迟[128]、积分器[129]、高阶滑模[130-132]等方法以克服压力抖动。

需要注意的是，“机速”是计算滑移率的关键变量，虽然机上可以通过总线从飞行控制系统获得机速的微分值，但由于现役机载总线往往无法满足刹车控制单元(Braking Control Unit, BCU)实时计算的需求，通常需要在基本轮速的采集信号基础上采用诸如卡尔曼滤波(Kalman Filtering, KF)[133-135]、非线性自适应滤波[136]、多类速度融合[137-138]、滑模观测器(Sliding Mode Observer, SMO)[139-140]以及多测量值融合估计[141]等方法进行估计，这也导致在滑移率跟踪控制中，都存在对传感器噪声敏感[142]的问题。为此有学者将减速率[143]和滑移率构成凸组合[144-145]，这种组合形式的跟踪目标在一定程度上可以在获得滑移率控制优势的同时降低对传感器精度的要求。

4.4 智能防滑控制

随着神经网络和智能学习类方法的发展，进一步突出了神经网络(Neural Network, NN)在处理不确定问题时的能力[146]，并且理论上它可以逼近任意复杂的非线性映射关系[147]。防滑刹车系统作为典型的多非线性和不确定系统，智能方法的应用具有巨大的潜力。虽然目前还没有成熟的智能防滑刹车控制算法，但从人工智能兴起以来已经有众多学者开始在防滑刹车领域从地面结合力识别、智能轮胎和防滑刹车控制等多个方面进行不同程度的尝试。

在神经网络和智能学习类方法爆发之前，为应对防滑控制问题中的非线性问题，一些学者通常是在专家经验的基础上研究基于模糊逻辑的防滑控制[148]。通过将模糊控制与自适应方法相结合以克服控制中的不确定性[149-150]。还有将模糊控制与滑模控制相结合[151-152]，使得在系统状态变化时表现出更强的鲁棒性。由于定义模糊规则多是基于经验判断，且需要耗费大量的精力进行规则尝试，采用具有自组织能力的模糊神经网络[153]可以自动生成和调整模糊规则。

伴随控制单元算力的提升，神经网络和学习能力成为智能的代名词。在地面结合状态识别方面，除了直接通过采集的飞机速度、减速率以及机轮减速率等信息训练 NN 以获得特定条件下所对应的最优滑移率[154]外，采用模糊理论[106，155]与 NN 相结合的方法可以有效提升其在复杂工况下识别的准确性。另外，智能轮胎[156-157]是新型传感器技术与智能技术相结合的尝试。所谓智能轮胎主要是通过在轮胎附近或内部增加光学[158-160]、声学[161-162]、加速度[163-167]等传感器测量与路面类型或摩擦相关的参数，进而利用单一或融合传感器信息[168-170]通过神经网络实现与不同路面的映射[171-172]。

鉴于刹车控制问题的复杂性，一般的神经网络经过训练后泛化性有限，采用深度神经网络[173]和动态神经网络[174]是应对这种复杂问题的一种途径。Poursamad[175]在反馈线性化的基础上，结合两个前馈神经网络通过反馈线性化来学习刹车过程的非线性特性，并且证明了控制器在李雅普诺夫意义下的在线权值自适应性和稳定性。

由于在实际应用中很少有机会获得真机的着陆数据[176]，通过仿真环境生成的训练数据很难评价其是否覆盖了外场试验中的所有非线性特征，进而难以保证其在外场试验时是否具有足够的泛化性以应对真机情况下的非线性扰动。

飞机防滑刹车的早期以开关式防滑控制为主，主要通过惯性传感器实现机轮减速率的测量，利用机械或简单的电气方法以开关状态驱动液压系统。而后，随着轮速采集技术的发展，依旧以机轮减速率为监控目标，采用模拟电子电路将刹车压力调制为类“三角波”的形式使得机轮减速率在一定范围内循环往复。这种压力调制的方法控制逻辑简单，对作动器和信号采集要求低，鲁棒性强，非常适合于追求高可靠性的航空领域，但该类方法在不同道面条件下刹车效率存在差异，尤其在中断起飞(Rejected Takeoff, RTO)条件和恶劣工况下存在地面结合力利用不充分的可能性。

自适应性是现代飞机防滑刹车控制的特征，在功能上它不仅需要快速识别着陆跑道的摩擦条件，还需要在一定程度上兼容外部由于不确定性阵风所引起的空气动力变化和不同装载情况所导致的载荷差异；克服系统内刹车盘摩擦系数变化、作动器延迟和起落架振动所带来的扰动。过去该技术仅被世界极少数公司所垄断，而国内相关研究团队的突破使中国具备了自主装备自适应防滑刹车系统的能力，有效提升了相关机型的竞争力。

虽然基于滑移率跟踪的自适应防滑控制算法在学术界广受欢迎，但真实航空中应用较少[12]，究其原因在于该类算法的实际应用对系统要求较高，目前所装备的传感器和执行机构还难以支持其达到航空安全运行的标准。而且刹车过程中诸多的不确定性致使道面识别算法在开发时设置的一些假设在实际中不成立，导致道面识别的成功率受到影响。另外，通过 LuGre 模型描述可知在同一路况下μ-λ曲线并不是固定的，为此通过单次识别路况后跟踪最优滑移率，其全程刹车最优性并不能保证。

目前，智能类防滑控制方法仅在特殊改装的汽车平台中实现测试，鲜有在飞机上试验成功的案例。在飞机上采用神经网络方法需要经过前期充分的试验验证，开发和应用成本较高，试验风险较大。并且飞机着陆条件更加复杂，神经网络在应对各种非训练工况下泛化能力存疑，这种不确定性所带来的可靠性问题能否达到航空应用标准是其进一步发展应用的关键。

5 仿真与试验验证

飞机防滑刹车控制律从设计到装机需要一套完整的开发流程，在保证安全和控制成本的前提下完成控制律的功能和性能验证。

5.1 全数字仿真

全数字仿真是防滑刹车控制算法最基本的验证方式，通过构建系统模型验证算法效果，模型环境的搭建需要尽可能与真实系统保持一致。对于传统的液压刹车系统仿真环境应至少包括液压系统模型、刹车装置模型、起落架模型、机轮模型、路面结合系数模型和机体模型，另外在有条件下情况下可以加入气动模型，引擎模型[177]以及个别机型的阻力伞模型[177-179]，如图23 所示。

在防滑控制律算法运行时，控制器输入端为机轮角速度ω和飞行员刹车指令信号ucmd。通常用阶跃或斜坡指令以模拟飞行员踩下刹车脚蹬的动作；液压系统接收来自控制器的控制信号uc，输出刹车作动器压力Pb，液压系统通常包括伺服阀模型、管路模型以及作动筒模型，由于该部分较为成熟，可通过与专业液压仿真软件 AMESim 等联仿完成；刹车装置模型将Pb转化为刹车力矩Tb。机轮起落架模型接收Tb以及来自地面模型的摩擦力矩Tf输出轮速ω，同时也将机轮载荷FL转换为地面支持力FN；路面模型以FN、ω和飞机速度Vp为输入，输出作用于机体的地面结合力Ff；机体模型在Ff、引擎残余推力Te、阻力伞阻力Fpara和气动阻力Fa作用下输出飞机速度Vp。

仿真模型精度是决定试验结果的关键。在不同的模型精度下，控制律的试验结果可能出现天壤之别。由于飞机刹车系统涉及多个复杂的非线性环节，搭建具有实践指导意义的仿真模型需要用大量惯性台及真机试验数据校核非线性模型参数，否则其验证结果仅能做定性参考。

5.2 硬件在环试验

硬件在环(Hardware In Loop, HIL)试验是将飞机刹车系统中部分成本可控的组件替换为真实器件，通过数字接口与计算机形成闭环测试环境。通常可以将控制盒与其他数字模型构成最小 HIL 环境，对防滑控制律及相关控制逻辑进行初步验证。Lee 等[180]为验证新型控制盒，构建了由五自由度飞机机体和机轮动态的数字模型、刹车控制盒及真实液压系统组成的 HIL 试验环境。Sun 等[25]构建的 HIL 环境是将伺服阀换为开关阀组，以验证开关阀的防滑刹车效果。Li 等[181]为 C919 型飞机 BCU 发了基于PXI总线架构的集成式飞机刹车控制器测试系统(图24)，该系统具有在线测试、离线测试和硬件在环仿真3种模式。

在线测试模式可采集和模拟正常装机态BCU相关信号；离线测试模式可为 BCU 提供电源管理、上电检测、相关模拟和数字输入接口的外设负载模拟以及输出接口的信号采集；硬件在环仿真模式是构建虚拟数字仿真环境，利用物理接口与 BCU 实现数据交互进而实现对 BCU的测试。

HIL 试验是惯性台和试飞着陆试验前有效的软硬件功能验证步骤，可以大幅降低试验成本，缩短控制律验证周期，尤其在研究系统局部特征时可以有效提升结果可信度。

5.3 惯性台试验

惯性台试验是目前在地面上最接近真机试飞着陆试验的验证方式，试验台主要由惯性鼓轮、电机、液压加载系统、刹车系统、控制盒及相关测控设备等构成，其总体架构如图25所示[70]。地面惯性台主要通过给机轮施加不同的载荷以模拟机轮的垂直载荷和不同的跑道变化，通过调整配重或电惯量补偿调节鼓轮惯量以模拟飞机质量。试验时电机驱动惯性轮达到飞机着陆速度，根据飞机质量和着陆能量输入电惯量补偿值；加载系统控制机轮与惯性轮之间的力达到设定值，当机轮与惯性轮速度基本相同时，试验操作人员给BCU刹车指令，进而BCU根据采集的轮速进行防滑刹车。

通常防滑刹车控制律在真机试飞前必须经过惯性台试验以验证控制律不同工况下的有效性和鲁棒性。

5.4 真机试飞着陆试验

在完成前述试验提供必要的安全基础后，真机着陆试验是刹车控制律应用装机的最终验证手段。NASA 和 FAA 曾在飞机/地面车辆跑道摩擦联合项目[182]中用改装型 B-737 飞机在不同路面条件下进行了上千次着陆试验以测试飞机的刹车性能。另外，FAA[35]、欧洲航空安全局(European Union Aviation Safety Agency, EASA)[183]及中国民航总局[184]在用于颁发飞行许可的系列测试项目中都有针对飞机刹车能力的严格测试规程。

6 展 望

6.1 典型刹车元件基础试验

具有自适应功能的防滑刹车系统，应能克服刹车过程中来自系统内外的各种扰动。但是在克服扰动，保证鲁棒性的同时往往以牺牲极致的效率为代价。牺牲效率的程度往往取决于对系统内典型元件的特征及元件在恶劣环境和长时间应用后退化水平的了解程度。

以传统飞机液压刹车装置为例，由于当前在役飞机刹车系统很少配备刹车力矩传感器，导致刹车控制中无法实现刹车力矩的闭环，即在同样的刹车指令下由于刹车盘材料特性在不同的速度，温度等条件下可能产生不同的刹车力矩。这种情况下如果没有大量样本数据提供刹车盘全生命周期的压力-力矩特性，则只能通过调整控制律阈值牺牲刹车效率，向保证安全妥协。因为机轮滑移状态在最大摩擦能力和控制鲁棒性间存在不可调和的矛盾，离最优滑移状态越近刹车效率越高，同时也意味着受扰后发生打滑的概率越大。为此，只有对系统内各元件进行大量独立和系统级基础试验，积累充足的样本数据，才能保证控制律相关参数的设计做到有的放矢。

在此方面，美国兰利研究中心曾投入巨资耗费数年时间进行大量机载、车载和人工试验[185]，研究比较关于不同刹车控制系统、轮胎磨损、刹车盘退化和作动装置响应等对飞机刹车性能的影响，用于进一步开发高效的防滑刹车系统。

6.2 高保真地面试验方式方法

飞机刹车控制律主要的验证方式主要是通过全数字仿真、HIL试验、地面惯性台测试[186]和试飞试验。对于当前竞争激烈的航空业，产品开发越来越快，提高全数字仿真模型的保真程度将有助于减少高成本的原型机数量。但是，在全数字仿真过程中，不仅工况条件可能与现实刹车过程存在差异，且在仿真过程中存在诸如刹车盘力矩系数难以进行数学建模的强非线性环节。对强非线性环节不同程度的简化，使得验证效果受到难以量化评估的影响。

虽然在 HIL 试验中对全数字系统中的部分组件进行了半实物化，但是受硬件条件限制，仅能用于验证部分功能性指标。惯性台试验是正式试飞试验前的关键性验证试验，但多数惯性台仅能通过改变机轮载荷模拟飞机在不同道路工况下的运行情况，这种试验方式不仅忽视了不同跑道随机轮滑移状态变化的差异，也忽略了飞机在着陆过程中可能存在的引擎残余推力、减速伞和飞机升力的变化，尤其难以表征飞机在侧滑条件下机轮结合力的变化情况，导致经过惯性台验证的控制律依旧难以在真实飞行过程中获得理想的效果。

为此，需要结合外场试验条件和飞机过往的飞行记录对惯性台试验进行优化，包括惯性台加载载荷谱的设计，不同条件下惯性鼓轮的电惯量补偿设计等。尽可能减少惯性台试验与真实试飞试验间的差距，以获得更具有试飞参考价值的地面试验结果。

6.3 智能刹车控制的可靠工程应用

智能技术的应用将有助于克服刹车过程特有的机轮最优滑移状态存在不确定性和时变性的问题。但是，当前智能技术在飞机刹车控制领域还没有较为成熟的应用案例。多源融合技术在状态预测和特征提取方面极具优势，而飞机刹车过程中机轮滑移状态的变化往往难以通过单一传感器直接采集。所以，利用不同传感器信息的有效融合可能获取比现有滑移率、减速率等状态更有利于防滑控制的变量类型，还可能一定程度预测机轮可能发生打滑的状态，进而在控制中利用前馈手段，避免机轮趋于打滑。

智能技术需要大量的训练数据，而获取真实飞机数据目前还没有公开的渠道，仅通过个别工况的离线仿真数据往往难以在真实飞机上获得安全可靠的应用。为此需要一种有效利用智能方法的控制架构，既可以保障飞机在刹车过程中不会由于训练样本有限而出现机轮抱死等严重影响刹车效率的情况，同时在典型工况下可以进一步提升飞机刹车的抗干扰性和刹车效率。