空间结构压杆的套管加固失效模式试验研究

曾 滨，许 庆，陈 映，王春林

(1. 中冶建筑研究总院有限公司，北京 100088；2. 东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

空间结构中关键压杆构件的稳定对整个结构的极限承载力有较大影响。空间结构中构件超载将会诱发单根杆件率先失稳，而这一失稳迅速引发荷载重分布并可能带来后续结构破坏[1-3]，如图1 所示。传统的加固压杆的方法有焊接钢板[4]、外粘钢板[5]或者纤维增强复合材料[6]，但是焊接会产生残余应力、粘贴结构胶存在耐久性等问题，阻碍了上述技术在空间结构压杆加固中的应用。所以，研发空间结构压杆构件加固新技术，提升结构的安全系数有着重要意义。

作为压杆稳定控制的一种方法，限制失稳技术也常被用来研发新型不失稳构件，如屈曲约束支撑[7-11]。如何利用限制失稳技术来提高空间结构压杆承载能力，从而提高结构极限承载力是本文重点关注的问题。如图2(a)所示，空间结构也可采用组装套管加固来限制压杆失稳[12]，形成套管构件提升压杆的承载能力。套管构件首次由SRIDHARA[13-14]提出，如图2(b)所示，由内压杆及外套管组成，两者之间预留一定间隙，当内压杆发生弯曲变形时，外套管为其提供侧向支承，限制其侧向变形，从而达到提高内压杆稳定承载能力的目的。

受压杆采用套管加固具有如下优点：① 经套管加固后形成的构件与原受压杆具有相同的初始刚度，带有套管加固构件的结构在承受设计地震作用时，其动力特性与原结构相同；② 套管加固方法不会引入新的应力集中源，不存在二次受力问题，也不用考虑加固构件与原构件的连接可靠性问题；③ 套管加固可以作为结构的第二道防线；④ 地震或强风荷载作用下结构中的受压杆件因为外套管的存在会延迟或者不会出现受压屈曲，实现了多道设防。

国内外学者对套管加固压杆及结构研究相对较少。SRIDHARA 等[14]的试验表明：套管构件失效时，内压杆截面上的平均应力已经超过材料的屈服应力。PDRASA[15]试验研究表明套管构件的受压承载能力相对于传统受压构件有大幅度提高。内压杆外伸段长度也是限制套管构件承载力的一个因素。申波[16]的研究表明：外套管的约束作用会提高内压杆的弯曲刚度，内压杆外伸段的存在会导致内核端部的局部屈曲破坏，从而影响套管构件的承载力。套管加固结构的研究目前主要停留在数值分析层面。胡波[17]分析了未加固和对应的用套管加固较危险受压杆件的空间结构模型，发现采用套管加固的方式能有效控制受压杆件的失稳问题，以及提高结构的极限承载力。

综上所述，受压杆经过套管加固后受压承载力有了显著提高，其空间结构的极限承载力也有了大幅提升，但是空间结构压杆套管加固试验仍然很少，其约束机制和失效模式仍不够明确。本文作为初探研究，将圆管作为加固外套管，直接搁置在内压杆外围，可在内压杆上自由滑动，如图2(b)所示。

通过12 根试件的试验研究，对比分析了外套管壁厚、内压杆与外套管之间的净间隙和内压杆外伸段长度等参数对套管加固压杆的极限承载能力和延性的影响，在此基础上提炼出套管加固压杆的失效模式。本文试验也将作为后续装配式外套管加固压杆试验研究的基础。

1 试件设计和加载

1.1 试件设计

如图3 所示，本文研究的套管试件主要由内压杆及外套管组成。表1 给出了所有套管构件S2～S12 的外套管设计尺寸，而S1 作为对比试件，仅有内压杆，表中并未给出。所有试件的内压杆尺寸相同，其杆长Lc、外径r和壁厚t0分别为2660 mm、70 mm 和4 mm。为了区分试件，按照外套管设计尺寸对试件进行命名。譬如试件L2400g2.5T2.5 表示该试件外套管长度L和厚度T分别为2400 mm 和2.5 mm，内压杆与外套管之间的间隙值g为2.5mm。进一步，表2 给出了试件加工完毕后的实测尺寸，S1*为所有内压杆实测尺寸平均值。

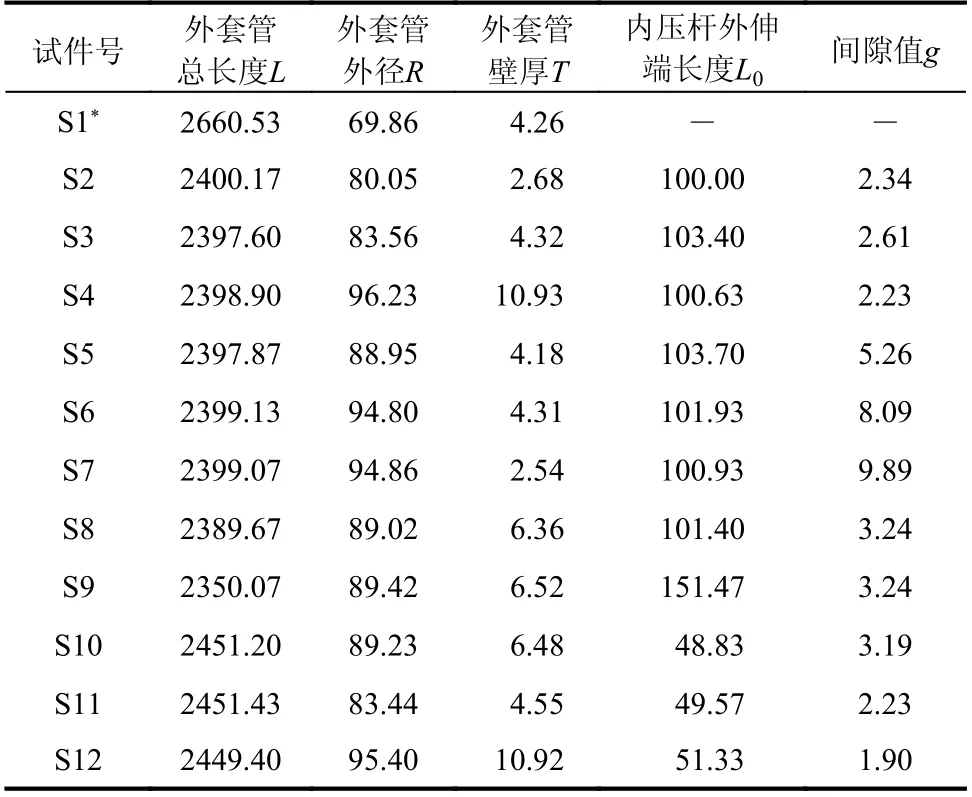
表2 试件实测尺寸 /mm Table 2 Measured values of specimens

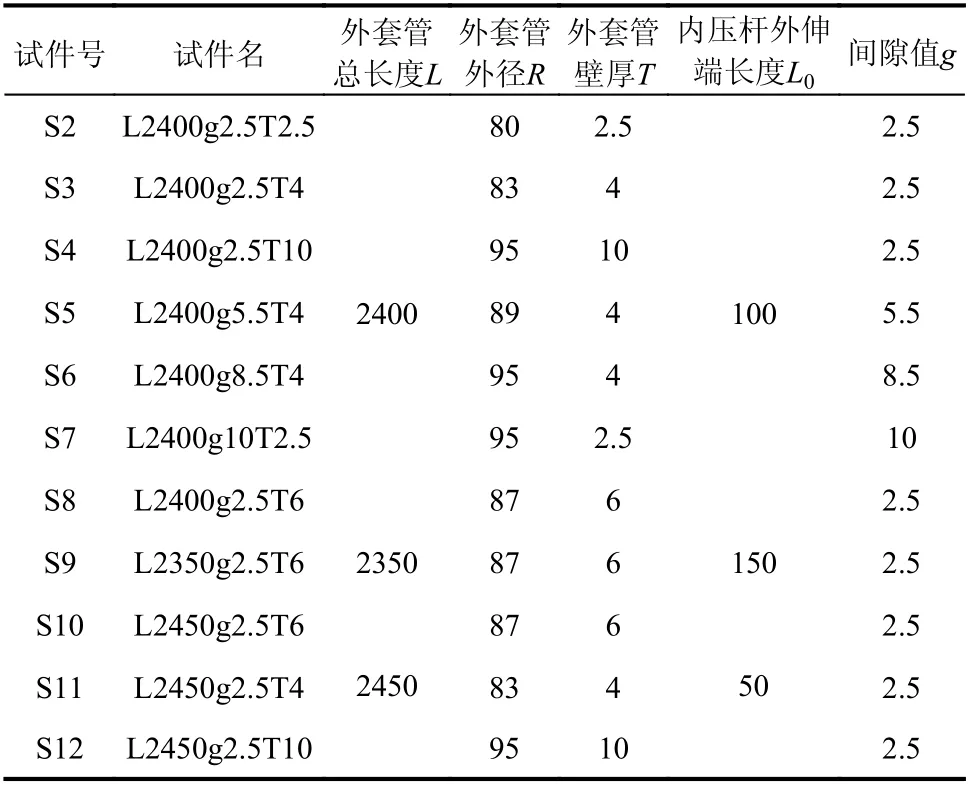
表1 套管设计尺寸 /mm Table 1 Design values of sleeves

1.2 材料性能

本次试验的内压杆和外套管都选用20#无缝钢管制作。依照《金属材料室温拉伸试验方法》(GB/T228.1-2010)[18]中相关规定加工试样，并进行了标准拉伸试验，材性试验结果如表3 所示。拉伸试样的命名遵循以下规则：RxTy代表试样由外径和壁厚分别为xmm 和ymm 的无缝钢管加工而成。以试样R70T4 为例，表示该试样由外径和壁厚分别为70 mm 和4 mm 的无缝钢管加工而成。

表3 材料性能参数Table 3 Material constants

1.3 加载装置及量测方案

本次试验为铰接构件的单向受压试验。图4给出了此次试验的加载装置，试验利用了500 T 液压长柱压力试验机的反力架，为了实现试件两端铰接，同时防止加载过程中的试件端部滑动，分别布置了单向刀铰和夹持装置，分别如图4(b)和图4(c)所示。构件下端刀铰板底部安装100 T 螺旋千斤顶，为防止千斤顶加载过程中失稳，在其顶部与试验机四个立柱之间设置了侧向支撑装置。

构件的实际转动中心位于刀铰的刀尖部位，端板厚20 mm，刀铰板厚25 mm，构件的计算长度应为构件的几何尺寸加上顶、底部两端的端板及刀铰板厚度，即两端分别加45 mm 可得实际计算长度。

试验的量测布置方案如图4(a)所示，构件的荷载F通过安装在试件顶部的压力传感器记录。构件跨中分别设置2 个水平方向的中部位移计用于测量套管构件在铰接方向的侧移。

在构件上下两端的端板四个角分别布置了4 个位移计用来测得端板的位移和转角。如图4(d)所示，以上端板为例，4 个位移计读数的平均值即上端板竖向位移h；4 个位移计读数也可以计算得到上端板转动过程中两侧边产生的竖向位移差值，竖向位移差值与端板两侧位移计水平间距(240 mm)的比值为端板的转角β。上端板的竖向位移h和转角β 的计算公式如下所示：

式中，c1、c2、d1和d2分别为上端板4 个位移计的读数。

试验过程中采取手动控制加载，分别读取压力传感器和位移计的数据，以获得构件的荷载-位移曲线。

1.4 加载模式

图5 给出了试件的加载制度[19]。加载前，为消除试件、连接件和试验机之间的空隙，需要对试件进行5 kN 的预加载，然后将荷载降到接近0 kN，荷载和位移计的读数清零。试验加载前先对试件进行了有限元模拟，预估了不同试件的峰值承载力。试验加载采用力控制和位移控制两阶段，第一阶段为施加荷载至20 kN 后降至10 kN，再施加荷载至30 kN 后降至10 kN，施加荷载至40 kN 后降至10 kN；接着开始第二阶段的加载，施加荷载达到模拟峰值承载力80%后，减缓加载速率，直至构件荷载下降到实测极限承载力的80%以下，停止加载，此时判定为试件破坏。此外，若加载过程中跨中侧移超过构件长度的1/25 或者内压杆端部外伸段局部变形过大时立即停止加载。

2 试件结果

2.1 峰值承载力

表4 给出了试件的极限承载力。由表4 可知，试件S2-S12 的极限承载力远高于试件S1，即压杆经外套管加固后，极限承载力提升较大。试件的荷载-位移曲线将在3.1 节中给出。

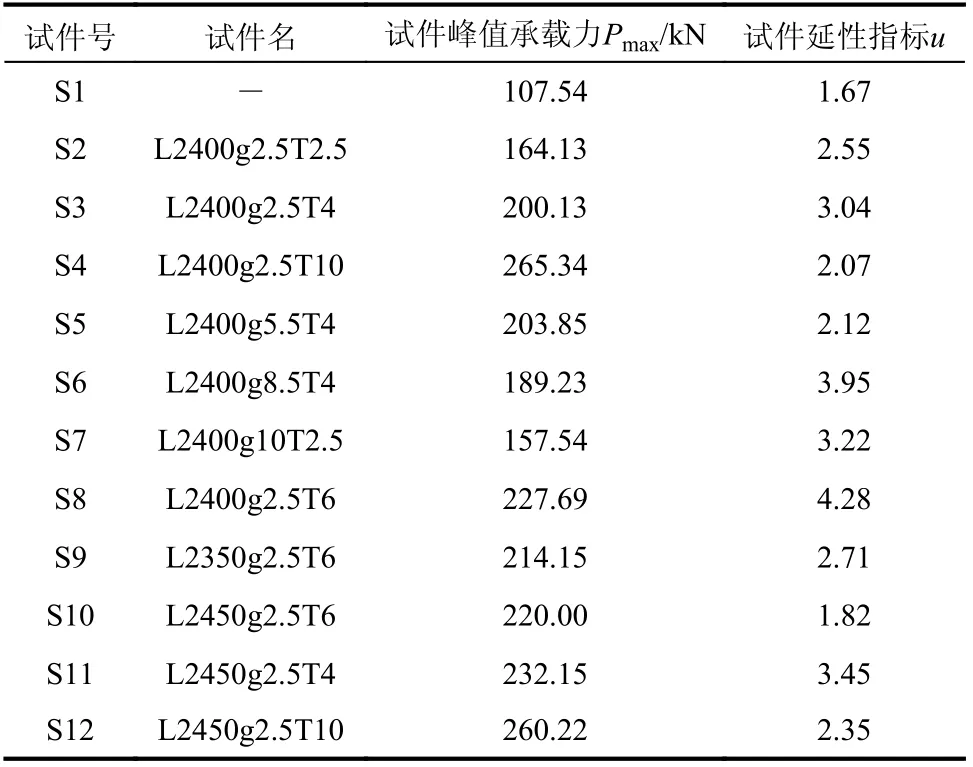
表4 试件试验结果Table 4 Test results of specimens

2.2 破坏模式

表5 进一步总结了所有试件的破坏模式，特别是给出了构件的整体失效图，以及内压杆上端部变形图。根据外套管变形和内压杆上端部变形初步将试件的失稳形态分为构件整体失稳、内压杆外伸段端部局部失稳、以及端部局部失稳与整体失稳耦合的破坏模式。

3 试件结果分析

3.1 试验参数分析

结合表2 和表4 可知，套管加固试件承载能力的提高受到多个参数的影响，其中包括外套管壁厚、内压杆与外套管之间的净间隙和内压杆外伸段长度等，分别对比讨论如下。

图6 对比了不同外套管壁厚对套管试件承载力的影响。其中，图6(a)对比了外套管长度相同，内压杆与外套管间隙相同时，S2、S3 和S4 的荷载-位移曲线，同时也给出了无外套管试件S1 的曲线。由图可知：1)进行套管加固后的试件承载力显著提高，相比试件S1，试件S2、S3 和S4 的极限承载力分别提高到1.53 倍、1.86 倍和2.47 倍；2)加载初期，未加固的试件与套管加固试件的刚度接近，初始刚度即为内压杆的轴向刚度；3)对于外伸段长度相同、内压杆与外套管间隙相同的试件，外套管壁厚越大，承载力越高，这是因为外套管越厚，抗弯刚度越大；4)结合表5的失效模式可知，内压杆外伸段长度和间隙相同时，套管壁厚较小时易发生套管试件整体失稳，套管壁厚较大时避免了整体失稳，但易发生内压杆外伸段局部失稳。图6(b)对比了S11 和S12 的荷载-位移曲线，也可以得到同样的规律。图7 分析了内压杆与外套管之间间隙的差异对套管加固试件承载力的影响。图7(a)给出试件S1、S2 和S7 的荷载-位移关系曲线。由图可知，试件S2 和S7 的间隙分别为2.5 mm 和10 mm，其极限承载力分别为164 .13kN 和157.54 kN，相对于试件S1 分别提高到极限承载力提高到1.53 和1.46 倍，而S7 相对于S2，极限承载力仅降低了4%。图7(b)对比了试件S3、S5 和S6 的荷载-位移曲线，内压杆外伸段长度均为100 mm，外套管壁厚均为4 mm。由图可知，试件S3、S5 和S6 的间隙分别为2.5 mm、5.5 mm 和8.5 mm，其极限承载力分别为200.13 kN、203.85 kN 和189.23kN。其中，间隙分别为2.5 mm 和5.5 mm 的两个试件S3 和S5，极限承载力相差不大，而间隙为8.5 mm的试件S6，相对于试件S3，其极限承载能力仅下降了5%。

表5 试件破坏模式Table 5 Failure modes of specimens

由此可得，当外套管壁厚与外伸段长度相等时，内压杆与外套管间隙对极限承载力影响较小，甚至当间隙分别为8.5 mm 和10 mm 时，其极限承载能力略有下降，分别降低了约5%和4%。考虑到对空间结构杆件进行套管加固，较大的容许间隙能够方便施工，但导致性能略有下降。

图8 对比了内压杆外伸段长度的差异对套管加固试件承载力的影响。图8(a)对比了试件S1、S3 和S11 的荷载-位移曲线，试件S3 和S11 的外套管壁厚都为4 mm，内压杆与外套管间隙都为2.5 mm，外伸段长度分别为100 mm 和50 mm，极限承载力分别为200.13 kN 和232 .15kN。由此可得，当压杆外伸段越短，承载力略有增加，增加了16%。

图8(b)对比了试件S4 和S12 的荷载-位移曲线，试件S4 和S12 的外套管壁厚为10 mm，间隙为2.5 mm，外伸段长度分别为100 mm 和50 mm，对应的极限承载力分别为265.34 kN 和260.22kN，二者的极限承载力相差不大。对比试件S3 和S11的外套管壁厚4 mm，表明S4 和S12 的外套管壁厚10 mm，对上部内压杆外伸段下端有着更强的约束，而这种更强的支承使得试件极限承载能力有所增加，同时也弱化了外伸段长度对极限承载能力的影响。

3.2 失效模式分析

图9 根据试验中试件的变形模式，给出了试件的整体失稳、内压杆外伸段端部失稳和端部失稳与整体失稳耦合的失效模式示意图，并结合试件的设计参数解释如下。

对比外伸段长度相同、内压杆与外套管间隙相同的试件S2、S3 和S4 发现，三个试件的外套管壁厚分别为2.5 mm、4 mm、10 mm，破坏形式分别为整体失稳(图9(b))、端部失稳和端部失稳(图9(c))，当外套管壁厚越薄时，越容易发生整体失稳。此规律也可以在S11 和S12 两构件中验证，其外套管壁厚分别为4 mm 和10 mm，破坏模式分别为整体失稳和端部失稳。

比较试件S2 和S7，外套管壁厚与内压杆外伸段长度相同，内压杆与外套管间隙相差较大，破坏模式都是整体失稳破坏；试件S3、S5 和S6 只有间隙有差别，但是破坏模式以端部失稳为主，因此，套管构件内压杆和外套管之间的间隙对破坏模式的影响不大。

试件S3 和S11 外套管壁厚相同，内压杆与外套管之间的间隙相同，外伸段长度为100 mm 的试件S3 的破坏模式为端部失稳，外伸段长度为50 mm的试件S11 的破坏模式为耦合失稳，即当套管构件其他尺寸相同时，内压杆外伸段长度越长，越容易发生耦合失稳破坏，反之，容易发生整体失稳。

进一步将上述试验现象总结如下：

如图9(a)所示，加载初期，存在初始缺陷的内压杆在一定的轴向压力作用下开始发生侧向变形，由于内压杆与外套管存在一定的间隙，初始阶段外套管并不受力，随着荷载的增大，内压杆侧向变形逐渐变大，外套管受到内压杆与外套管接触力的作用，从而发生侧向挠曲，内压杆与外套管的侧向挠曲随着荷载的增大缓慢发展。

当外套管厚度较小时，外套管不足以承担内压杆的作用力，导致外套管发生较大的弯曲变形，此时到达峰值荷载，承载力将逐渐下降，试件发生整体失稳，试件的失稳形态如图9(b)所示；当外套管厚度较大时，外套管弯曲刚度较大，内压杆与外套管接触力作用下弯曲变形也较小，而此时内压杆的外伸段由于没有套管约束，也会发生绕外伸段底部的转动，当外伸段底部形成塑性铰时，试件成为机构，试件发生端部失稳，承载力将逐渐下降，试件的失稳形态如图9(c)所示；当外套管厚度适中时，在内压杆与外套管接触力作用下外套管发生较大弯曲变形同时，外伸段底部也形成塑性铰，试件发生套管整体失稳与外伸段失稳的耦合失稳，承载力将逐渐下降，试件的失稳形态如图9(d)所示。

3.3 延性分析

4 试件数值模拟

4.1 数值模型

如图11 所示，给出了套管构件的数值模型。内压杆、外套管、上(下)夹持装置和上(下)端板均使用C3D8R 实体单元，网格尺寸均为10 mm 左右，内压杆和外套管均沿径向划分为2 层单元。数值模型使用的材料属性如表3 所示。为考虑内压杆的几何初始缺陷，对内压杆进行线弹性屈曲分析，在进行套管构件静力分析时，引入内压杆的一阶屈曲模态作为内压杆的初始缺陷，内压杆的初始缺陷幅值为Lc/1000，未考虑外套管的初始缺陷。

夹持装置与端板在试验加载过程中未产生相对滑动，建模时使用绑定约束(Tie)功能，将夹持装置与端板的接触面进行绑定约束。内压杆、外套管、和端板(夹持装置)之间通过接触传递压力，使用通用接触(Contact)功能，接触面间的法向(Normal)定义为硬接触，接触面间的切向(Tangential)定义为罚函数接触算法。

如图11 所示，在套管试件加载装置刀铰的刀尖位置分别建立两个参考点，其与内压杆上、下端面的距离均为45 mm，通过耦合(Coupling)功能，将上、下参考点分别与上、下端板端面的6 个自由度进行耦合。对于套管试件下端的加载点，约束沿X、Y轴的平动自由度以及绕Y、Z轴的转动自由度(UX=UY=URY=URZ=0)；对于套管试件上端的耦合点，约束沿X、Y、Z轴的平动自由度以及绕Y、Z轴的转动自由度(UX=UY=UZ=URY=URZ=0)。

根据外套管的受力特性，约束外套管跨中截面沿X轴的平动自由度以及绕Y、Z轴的转动自由度(UX=URY=URZ=0)。通过在试件下端加载点施加位移荷载对套管试件进行轴向加载，采用自动增量步进行非线性数值分析。

4.2 荷载-位移曲线对比

如图12 所示，给出了典型试件的荷载-位移曲线对比图。由图7 知，试件S2 数值模拟的荷载-位移曲线与试验结果差异不大；试件S11 和S6 数值模拟的极限承载力与试验结果差异不大，荷载下降阶段曲线略低于试验结果。

4.3 试件失效模式对比

如图13 所示，给出了典型试件的失效模式对比图。由图13 可知，试件S2 外套管跨中截面边缘纤维进入塑性，试件发生整体屈曲破坏；试件S11 外套管跨中截面边缘纤维进入塑性，试件发生整体屈曲破坏，同时，内压杆外伸段与外套管接触截面边缘纤维进入塑性，试件发生端部屈曲破坏，最终发生耦合屈曲破坏；试件S6 内压杆外伸段与外套管接触截面边缘纤维进入塑性，试件发生端部屈曲破坏。

5 研究展望

第3 和4 节将简单圆管作为外套管，通过试验和数值模拟证明了采用圆管加固能高效提升压杆的承载能力。图14 为装配式套管构件构造，将无缝钢管切割成两个半圆钢管，在半圆钢管两侧边焊接带有螺栓孔的缀板，通过螺栓锚固形成装配式套管，直接搁置在压杆上。使用该类装配式外套管，可实现在役状态下对压杆进行加固，提升空间结构压杆加固的工作效率。

6 结论

文针对空间结构的压杆研究了采用套管进行加固后的性能。通过 12 根试件轴压试验对比研究发现，此方法能显著提高构件的极限承载能力，加固后试件的极限承载能力最高提高了147%，延性指标最高提高了 156%。并进一步分析了关键参数对试件的承载力、失效模式和延性指标的变化。建立了套管构件的数值模型，并与试验结果进行了对比。主要结论如下：

(1) 所有经过套管加固的试件，承载力均有大幅度提高：对于外伸段长度相同、内核与外套管间隙相同的试件，外套管壁厚越大，承载力越高；外套管壁厚与外伸段长度相等时，内核与外套管间隙越大，承载力越低；外套管壁厚与间隙相等时，外伸段越长，承载力越低。

(2) 结合试验现象，套管试件的破坏模式有，整体失稳、内压杆外伸段端部失稳和两种失稳状态耦合破坏。当外套管壁厚越薄，越容易发生整体失稳破坏，内压杆外伸段长度越长，越容易发生端部失稳破坏，加固试件的内压杆和外套管之间间隙对破坏模式影响较小。

(3) 套管加固试件的延性系数均大于未经加固的内压杆，加固后构件可以承受更大的塑性变形而不破坏，经过合理设计延性指标能够增加一倍以上。

(4) 根据试件的受力特性，建立了套管构件的数值模型，得到极限承载力和失效模式与试验结果一致，表明该建模方法能有效模拟轴压套管构件的静力性能和失效模式。