基于极上限分析的临水深基坑围护结构主动土压力计算

2022-11-05关振长黄金峰何亚军宁茂权

工程力学 2022年11期

关振长，黄金峰，何亚军，宁茂权

(1. 福州大学土木工程学院，福建，福州 350116；2. 中铁第四勘察设计院集团有限公司，湖北，武汉 430064；3. 海峡(福建)交通工程设计有限公司，福建，福州 350004)

随着我国城市地下工程建设的不断发展，近年来出现了许多沿江临河修建的深基坑工程。基坑临水岸坡与基坑围护结构构成的有限宽度土体，其失稳破坏模式及土压力计算方法，与无限宽度土体条件下的土压力计算模式有较大不同，诸多学者基于极限平衡法与极上限分析法对此展开深入研究。

CHEN 等[1]基于极限平衡法与平面滑裂面假定，建立了有限宽度土体的主动土压力公式，探讨了墙后有限土体宽度对破裂角和土压力的影响。王闫超等[2]和HU 等[3]采用薄层法推导了有限宽度土体条件下，作用在基坑围护结构上的主动土压力解析解。高幸等[4]和应宏伟等[5]分别基于极限平衡的理论计算与数值模拟，考虑基坑宽度和深度等因素，探讨空间效应对围护结构主动土压力分布的影响。徐日庆等[6]和MIAO 等[7]基于塑性上限理论与平面滑裂面假定，推导有限土体的主动土压力解析式，分析土体内摩擦角、土体宽高比、地震力和超载对主动土压力的影响。李志浩等[8]、XU 等[9]和YANG 等[10]基于极上限理论和对数螺旋滑裂面假定，重点关注地震作用对悬臂挡墙、加筋挡墙主动土压力的影响。HUANG 等[11]、LIU[12]基于极上限定理与多块体速度场理论，分别探讨了地震作用下土体的抗剪强度参数、上下游水位对挡墙滑裂面与稳定性的影响。

对于非均质土层，MOLLON 等[13]提出了离散化滑裂面生成技术，并基于极上限法分析了非均质地层抗剪强度参数对隧道掌子面土压力的影响。PAN 等[14]则进一步推导了隧道掌子面极限支护力的解析式，分析了非均质地层抗剪强度参数对隧道掌子面稳定性的影响。SUN 等[15-16]和QIN 等[17]利用极上限分析法和离散化滑裂面生成技术，分别探讨了坡体的抗剪强度参数、坡顶超载、几何形状及降水条件对边坡稳定性和库岸边坡安全系数的影响。

综上述，极上限分析和多线段滑裂面生成技术，能较好地解决非均质土体的稳定性分析与土压力计算问题。本文将其应用于沿江临河修建的深基坑工程中，推导临水深基坑围护结构主动土压力的上限解，并与传统土压力理论计算结果相互验证。进一步依托农林大学站工程实例，开展多工况算例分析，探讨坡坑宽高比及水位条件对基坑围护结构主动土压力上限解的影响，以期为临水深基坑工程围护结构的科学设计提供参考。

1 多线段滑裂面

沿江临河修建的地铁车站或高层建筑基坑，临水岸坡与围护结构构成了有限宽度土体，失稳破坏时滑裂面不能延伸至地表，而是相交于临水岸坡面，其滑裂面形态如图1 中模式Ⅰ所示。需要说明的是，当坡顶面宽度较大时，则滑裂面相交于坡顶面(如图1 中模式Ⅱ所示)，即与传统无限宽度土体的情形趋于一致。

基坑开挖深度为H，坡顶宽度为L，水位面与坡顶高差为h0，临水岸坡坡角为α，坑底延长线与河底相交于D点。墙后土楔ABCE(或EBC)为刚体，可沿滑裂面EC做刚体转动。q为坡顶均布超载，w为坡面三角形分布水压力，Ea为围护结构土压力的反作用力。基坑围护墙的嵌固端较强，因此可认为滑裂面由起始于坑底墙趾C点，并与岸坡交于E点的系列多线段PiPi+1组成[15-16]。以C点为原点建立平面直角坐标系，根据极上限定理，土楔ABCE(或EBC)绕旋转中心O(假定其横纵坐标分别为xO和yO)以恒定的角速度ω转动。

以第一微元块OCP1为例(如图2 所示)，说明各离散点Pi坐标的确定方法。微元块中C点的旋转角θ1可表达如式(1)；C点的线速度vC垂直于OC，且与P1C的夹角即为土体内摩擦角φ1，则OC与P1C的夹角为π/2-φ1；OP1与OC的夹角为Δθ，因此在微元块OCP1中，根据正弦定理可得OP1的长度如式(2)所示。

根据式1～2，求得第一微元块中P1的横纵坐标如式(3)所示。

利用递推式3，从点C出发，当点Pn落在坡面AD或坡顶AB上时终止，由此可求得多线段滑裂面EC上的所有离散点坐标。需要说明的是：Δθ 的取值对于计算精度有重要影响，根据前人的研究，Δθ 可取为0.1°[17]。

2 基于极上限的围护结构土压力计算

根据极上限定理，土楔ABCE(或EBC)中所有外力(重力、坡顶超载、岸坡水压力、围护结构土压力)所做功率不能超过滑裂面上的能量耗损功率，通过功率平衡方程，可得到围护结构主动土压力的上限值[8-9]。

2.1 重力功率

对于模式I，土楔ABCE自重所做功率为块体WEGC与块体WAEGB的组合，如图3(a)所示。将块体EGC沿滑裂面EC的离散点进行水平条分，得到若干个梯形块，需要说明的是，水位面以上取土体的天然重度，水位面以下取土体的饱和重度。梯形块所做功率如式(4)所示。其中，γi为微元梯形土条所在土层的重度，Si、xi分别为梯形块的面积与形心横坐标。

对图3(a)所示的梯形块PiPi+1TiTi+1，根据滑裂面EC上各离散点坐标，计算各梯形块顶点坐标、形心坐标及面积；将其代入式(4)，化简后可得重力功率如式(5)所示；将每个梯形块的重力功率累加，可得块体区域WEGC的重力功率，如式(6)所示。

同理，将块体AEGB沿坡面AE进行水平条分，得到若干个梯形块TjTj+1Pj+1Pj，如图3(a)所示。计算梯形块的各顶点坐标，并将其代入式(4)，化简可得重力功率如式(7)所示。将每个梯形块的重力功率累加，可得块体区域WAEGB的重力功率，如式(8)所示。

对于模式Ⅱ，取出微元梯形块PiPi+1TiTi+1，如图3(b)所示，根据滑裂面EC上各离散点坐标(由式(3)可得)，计算各梯形块顶点坐标、形心坐标及面积，并将其代入式(4)，化简可得功率如式(5)所示。将每个梯形块的重力功率，进行累加得到滑裂体WEBC所做的重力功率，如式(9)所示。

2.2 坡顶超载与水压力功率

临水坡面EF段承受水压力w作用，如图4 所示，rw、vw为坡面任意点处的半径与线速度，η 为该点处水压力与vw的夹角，各表达式分别如式(10)、式(11)和式(12)所示。则水压力所作功率可积分表达，如式(13)所示。

坡顶承受均布超载，如图4 所示，vq为坡顶任意点处的线速度，则超载功率的表达式分别如式(14)(模式Ⅰ)和式(15)(模式II)所示。其中，γw为水的重度，h1为水位面与滑裂点E的高差，其余参数物理意义与图1 中相同。

2.3 围护结构主动土压力功率

围护结构BC承受主动土压力作用，Ea为其反作用力，作用点高度假定距C点1/3 基坑深度处，与水平方向夹角为墙土接触摩擦角φ'[8-18]；vTE为作用点处线速度，如图4 所示。可求得围护结构主动土压力的功率WEa如式(16)所示：

2.4 内能耗散功率

能量耗散仅发生在滑裂面EC上，如图4 所示，考虑非均质土体，能量耗散Qc可由离散线段PiPi+1上能量耗散功率累加求得，如式(17)所示。将各离散点坐标代入式(17)中，则内能耗散功率表达式如式(18)所示。其中，ci、φi分别为离散线段PiPi+1所在土层的黏聚力与内摩擦角。

2.5 主动土压力上限解的计算

根据极上限定理，外力所作功率与内能耗散功率应满足式(19)：

对于模式Ⅰ，分别将式(6)、式(8)、式(13)～式(14)及式(16)～式(17)代入式(19)，整理得围护结构主动土压力Ea的上限解，如式(20)所示。对于模式Ⅱ，分别将式(9)、式(15)～式(17)代入式(19)，整理得围护结构主动土压力Ea的上限解，如式(21)所示。

需要说明的是，主动土压力是旋转中心O点坐标的函数，通过遍历所有可能的O点坐标，使得墙背主动土压力Ea(式(20)或式(21))取得极大值，即为围护结构主动土压力的极上限解。

3 算例验证

单一均质地层情况下，将上述计算方法与传统计算方法相比较[8]。选取临江基坑围护结构墙高H=10 m，坡角α=45°，坡顶宽度L=3 m，水位面与坡顶高差h0=1 m，土体天然重度γ=16 kN/m3，土体饱和重度为γsat=18 kN/m3，超载q=0 kPa。令黏聚力c、内摩擦角φ分别在6 kPa～14 kPa、20°～28°之间变化，计算围护结构主动土压力的上限解，如表1 所示。

由表1 可知，随土体物性参数的变化，各种方法计算所得主动土压力的变化规律一致。本文方法与假定直线或对数螺线滑裂面的传统方法相比，其主动土压力最大差异仅为2.48%和1.87%。事实上，在均质地层情况下，当微元梯形土条划分足够细小，多线段滑裂面即趋向于传统对数螺线滑裂面，本文方法所得主动土压力的上限解趋向于传统方法。

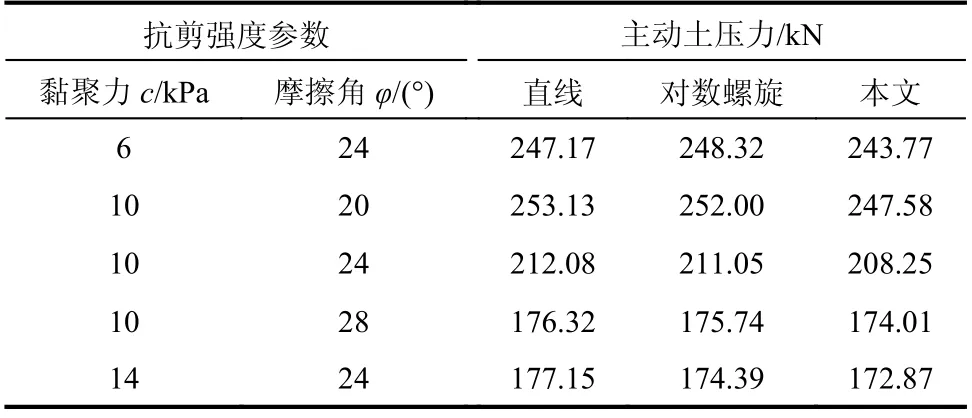
表1 主动土压力计算结果对比Table 1 The comparison of active earth pressure calculated by deifferent methods

4 工程实例分析

4.1 农林大学站工程概况

福州市轨道交通5 号线农林大学站位于福州市仓山区上下店路道路下方，呈南北走向。地层自上而下依次为粉质黏土、淤泥质土、残积砂质黏性土及全风化花岗岩，各土层的主要物理力学参数如表2 所示[19]。需要说明的是，水位以下河底以上的土层，重度采用饱和值，抗剪强度指标采用有效值，如表2 方格右侧数值所示。

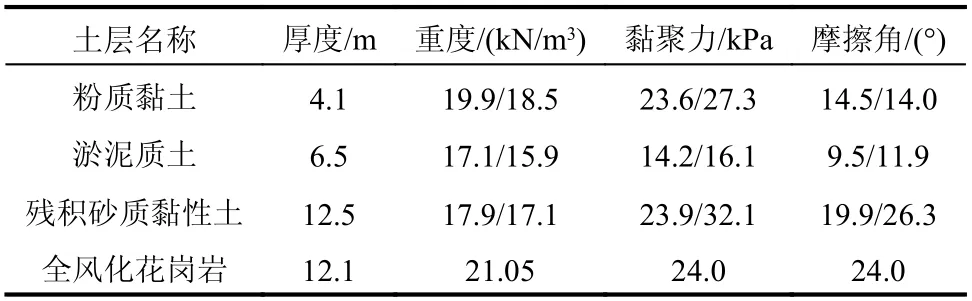
表2 地层物理力学参数表Table 2 The physical and mechanical parameters of ground

车站基坑开挖深度为23.1 m，东侧紧邻闽江，闽江河堤距基坑L=7 m～18 m，岸坡坡度约α=30°，堤岸高程约为10.2 m；受季节影响，闽江下游水位面高程在2.1 m～8.3 m 波动(罗零高程)，地表承受20 kPa 的均布荷载，其计算简图如图5所示。

4.2 主动土压力的敏感性分析

根据农林大学站实际工况(H=23.1 m，坡角α=30°，q=20 kPa)，令水位面与坡顶高差h0在2 m(高潮位)～8 m(低潮位)变化，坡坑宽高比L/H在0.3～0.8 变化。根据本文方法求得基坑围护结构主动土压力的上限解如图6 和图7 所示。

由图6 可知，水位面与坡顶高差h0对主动土压力的影响较为显著。围护结构主动土压力随水位上升呈近似线性增大，以L/H=0.3 工况为例，当水位面与坡顶高差h0从8 m 减小至2 m，则围护结构主动土压力增大10.6%。

由图7 可知，围护结构主动土压力随坡坑宽高比L/H的增大，先快速增长后趋于稳定。当坡坑宽高比L/H大于0.7 左右时，主动土压力趋于稳定，说明滑裂面由模式Ⅰ(相交于坡面)过渡到模式Ⅱ(相交于坡顶)，即墙后土体由有限宽度过渡为半无限宽度，这与前人研究成果是一致的[20]。

4.3 与数值模拟的对比

根据农林大学站实际工况，在FLAC 平台上建立车站基坑开挖的数值模型[21-22]。坡坑宽高比L/H=0.7，水位面与坡顶高差h0=5 m，土体采用摩尔库伦本构模型，主要物性参数如表2 所示；具体开挖工况及支撑参数详见文献[21]。

开挖支撑至坑底后，通过不断折减支撑刚度，当支撑刚度折减0.5 倍时，墙后土体逐渐达到主动极限状态，从塑性剪应变云图中可明显观察到滑裂面延伸至坡面或坡顶，如图8 所示。可知滑裂面以多线段形式从墙趾开始向两侧延伸，临江侧滑裂面交于坡肩，这与前述理论推导中的假定亦较为吻合。

达到主动极限状态时，读取临江侧围护墙的土压力分布，如图9 所示。其主动土压力沿深度大致线性增大，在接近坑底处取最大值149.6 kPa。进一步，求得主动土压力的合力为1769.6 kN，合力作用点距墙趾以上8.12 m 处(接近坑深1/3)；与本文方法计算所得主动土压力1841.4 kN(见图6 或图7 中的实际工况)基本吻合。