地震-风耦合作用下钢框架-自复位支撑筒结构性能研究

2022-11-05徐龙河刘媛媛谢行思

工程力学 2022年11期

徐龙河，刘媛媛，谢行思

(北京交通大学土木建筑工程学院，北京 100044)

自复位耗能(self-centering energy dissipation，SCED)支撑因兼具良好的耗能和复位能力，成为近年来结构抗震领域的研究热点。在地震发生时，SCED 支撑可为结构提供抗侧刚度，有效保护主体结构的安全、减小残余变形，从而降低整体震后修复成本及修复难度，快速恢复结构使用功能。国内外学者针对SCED 支撑结构的抗震性能已开展了大量研究。ZHANG 和ZHU[1]将由形状记忆合金提供自复位能力的SCED 支撑应用于3 层钢框架结构，研究了形状记忆合金的初始预张力对结构抗震性能的影响。结果表明，无预张力的支撑具有更好的自复位能力，能更有效地控制结构的残余变形；有预张力的支撑耗能能力更强，对控制结构的层间变形和加速度响应更有效。刘璐等[2-3]给出了防屈曲SCED 支撑钢框架结构的三线性恢复力模型，并对比了该结构和防屈曲支撑钢框架结构的抗震性能。结果表明，防屈曲SCED 支撑钢框架结构具有更强的抗震性能，其最大层间位移和残余变形均更小。徐龙河等[4-7]提出了多种由组合碟簧提供复位力、通过摩擦或阻尼装置耗能的新型SCED 支撑，往复荷载试验表明，支撑具有稳定的旗形滞回响应，能有效减小框架结构的地震响应及残余位移。徐龙河等[8]还提出了预压碟簧自复位耗能(pre-pressed spring self-centering energy dissipation, PS-SCED)支撑-钢框架结构的等效阻尼比公式，该公式能够用于PS-SCED 支撑-钢框架结构直接基于位移的抗震设计。

然而，现有的SCED 支撑结构通常为低层和多层结构，且主要基于传统的仅考虑单一灾害影响的方法进行设计，而多灾害耦合作用下的结构性能还有待深入研究。作为最为常见且通常对结构性能起到控制作用的两类荷载，地震与风灾害一旦同时发生，其耦合作用会对结构性能提出更高的要求。刘杨等[9]对钢管混凝土框架-防屈曲支撑结构在地震-风耦合作用下的易损性进行了研究，结果表明，随着风荷载强度的增大，结构的反应和易损性均有增大趋势。ZHENG 等[10]考虑不同强度地震动和不同强度风荷载的随机组合，提出了高层建筑在地震-风耦合作用下的破坏风险评估框架，并将其应用于位于大理的某42 层钢框架-钢筋混凝土核心筒结构分析评估中。结果表明，地震-风耦合作用下结构的损伤概率通常大于地震和风荷载单独作用下的结果。

可见，地震与风灾害是结构服役期间面临的主要威胁，尤其对于风荷载敏感的高层结构，地震-风耦合作用对结构性能的影响不容忽视。本文基于线性滤波法的自回归(auto-regressive，AR)模型分别模拟1 年、10 年和50 年重现期(分别记为R1、R10 和R50)下不同高度处的风荷载记录，对一50 层钢框架-PS-SCED 支撑筒结构进行非线性响应模拟，揭示不同强度的地震和风耦合作用对结构性能的影响规律，评价结构在多灾害下的性能。

1 钢框架-PS-SCED 支撑筒结构

1.1 结构信息

50 层钢框架-PS-SCED 支撑筒结构位于北京的Ⅱ类场地，首层层高为4.2 m，其余层高均为3.8 m，总高为190.4 m，结构平面布置如图1 所示。

该结构基于中国《建筑抗震设计规范》(GB 50011-2010)[11]进行设计，属丙类建筑，抗震等级为二级，设计地震分组为第一组，抗震设防烈度为8 度，设计基本地震加速度为0.2g，特征周期Tg为0.35 s。50 年基本风压为0.45 kN/m2，地面粗糙度为C 类。梁、柱构件均采用Q345 号钢材，截面信息列于表1 和表2。

表1 梁截面信息Table 1 Cross-sectional information of beams

表2 柱截面信息Table 2 Cross-sectional information of columns

表3 为该结构中PS-SCED 支撑设计参数。图2为PS-SCED 支撑构造及滞回曲线[4]。图中，P0为碟簧预压力，F0为摩擦装置提供的摩擦力。支撑在受拉或受压过程中，其力学性能可根据刚度变化分为4 个阶段：第1 阶段支撑内外管未发生相对滑动，此时支撑刚度由内外管及碟簧共同提供，称为第一刚度K1；第2 阶段内外管开始发生相对滑动并逐渐达到支撑最大位移，此时支撑刚度主要由碟簧提供，称为支撑第二刚度K2；第3 阶段支撑开始卸载，此时内外管无相对滑动，支撑刚度为K1；第4 阶段内外管再次发生相对滑动，支撑逐渐恢复至初始位置，支撑刚度为K2。

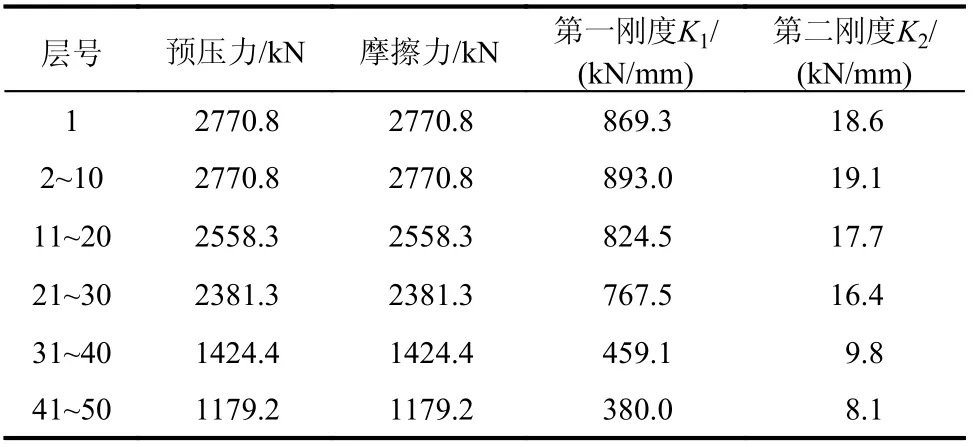
表3 PS-SCED 支撑设计参数Table 3 Design parameters of PS-SCED braces

该结构中，PS-SCED 支撑筒抗侧刚度大，承担大部分水平荷载，外框架延性性能好，承担大部分竖向荷载，两者协同工作，提高结构性能，同时减轻整体结构损伤，降低震后残余变形。

1.2 数值模型

在通用有限元分析软件LS-DYNA 中对上述钢框架-支撑筒结构进行建模，数值模型如图3 所示。

梁柱构件利用梁单元和双线性等向强化模型进行模拟，梁柱间刚接；楼板利用壳单元和线弹性模型进行模拟；PS-SCED 支撑采用杆单元和能够准确描述该支撑旗形滞回特性的二次开发子程序[5]进行模拟，支撑与框架之间铰接。

2 风荷载及地震动记录模拟

2.1 风荷载模拟

风速时程的数值模拟方法主要分为谐波合成法和线性滤波法，其中线性滤波法的AR 模型因其计算量小、计算效率高等优势得到了广泛应用。本文基于AR 模型进行脉动风速的模拟[12-13]。

根据《建筑结构荷载规范》(GB 50009-2012)[14]的规定，结构所在北京地区R1、R10 和R50 的基本风压分别为0.1 kN/m2、0.3 kN/m2和0.45 kN/m2。根据风速与风压的关系：

式中：ω0为基本风压； ρ为空气密度，取1.2 kg/m3；v0为10 m 高度处的基本风速。因此，计算可得R1、R10 和R50 的基本风速分别为12.91 m/s、22.36 m/s 和27.39 m/s。

风速由平均风速和脉动风速组成，平均风速根据《建筑结构荷载规范》[14]的规定沿高度变化采用指数函数表示：

式中：z为任意一点高度；v¯为平均风速函数；v¯0为10 m 高度处平均风速； α为地面粗糙度指数，地面粗糙度C 类对应 α为0.22。

脉动风速采用Kaimal 风速谱进行模拟[9]：

本文分析的钢框架-支撑筒结构共50 层，每两层可划分为一个区域，取各区域两层交界处为模拟风荷载作用位置，共得到25 个作用点，风荷载沿x方向作用。基于AR 模型对时长为100 s 的脉动风速进行了模拟，模拟时间间隔取0.02 s。图4为第10 和第20 作用点在R10 下的脉动风速时程v(t)，图5 为两作用点处模拟脉动风速谱与目标Kaimal 谱的对比，由图可知，模拟谱与目标谱吻合较好。

根据平均风速函数和模拟所得的脉动风速时程，可计算得出风荷载Fi时程[9]：

2.2 地震动记录模拟

根据结构抗震设防烈度、建筑场地类别和设计地震分组，生成地震反应谱，据此在美国太平洋地震工程研究中心地震动数据库中选取7 条地震动记录，其详细信息列于表4，所选地震动记录的平均加速度反应谱与规范谱的对比如图6 所示，可见两者吻合较好。经验算，结构基底剪力在所选地震动作用下满足《建筑抗震设计规范》[11]的要求。结构底层柱底与地面固结，地震动记录沿x方向输入。

表4 地震动记录信息Table 4 Information of the earthquake records

3 地震-风耦合作用下结构性能

为研究钢框架-PS-SCED 支撑筒结构在不同强度地震动和风荷载耦合作用下的性能，将7 条地震动记录的峰值地面加速度(peak ground acceleration，PGA)对应小震、中震、大震和巨震4 种强度分别调至0.7 m/s2、1.96 m/s2、4 m/s2和5.88 m/s2，每种强度的地震动记录分别与R1、R10 和R50 的风荷载进行组合，分析地震-风耦合作用、地震单独作用和风荷载单独作用下结构的响应及支撑工作状态。模拟总时长为150 s，其中风荷载自0 s 起持续加载至100 s，地震荷载从30 s起开始加载，100 s～150 s 为空白波，结构发生自由振动以测算其残余变形大小。前5 s 的风荷载需乘以时间t的形函数N(t)=t/5，以减小由于其突然作用导致的结构不稳定[9]。

本文中结构层间位移角、层间变形集中系数、结构耗能、残余变形角、基底剪力、PSSCED 支撑筒剪力占比与加速度放大系数均取7 条地震动单独作用或耦合风荷载作用下的平均值。

3.1 结构层间位移与支撑滞回特性

图7 为地震单独作用及耦合风荷载作用下结构各层最大层间位移角均值。在相同地震动强度下，随着风荷载强度的增大，结构最大层间位移角逐渐增大，但增量较小。地震分别耦合R1、R10和R50 风荷载作用下，当PGA 为0.7 m/s2时，结构最大层间位移角分别为0.26%、0.32%和0.37%，风荷载从R1 增至R10 及从R10 增至R50 时结构最大层间位移角的增量分别为0.06%和0.05%；PGA为1.96 m/s2时，结构最大层间位移角分别为0.65%、0.71%和0.75%，增量分别为0.06%和0.04%；PGA为4 m/s2时，结构最大层间位移角分别为1.05%、1.12%和1.16%，增量分别为0.07%和0.04%；PGA为5.88 m/s2时，结构最大层间位移角分别为1.43%、1.48%和1.52%，增量分别为0.05%和0.04%。可见，风荷载强度对结构层间位移角的影响并不显著，在相同地震动强度下，风荷载从R1 增至R10 及从R10 增至R50，结构最大层间位移角的增量均不超过0.1%。

在相同风荷载强度下，随着地震动强度的增大，结构最大层间位移角明显增大。在R1 风荷载作用下，地震动PGA 从0.7 m/s2增至1.96 m/s2、从1.96 m/s2增至4 m/s2以及从4 m/s2增至5.88 m/s2，结构最大层间位移角的增量分别为0.39%、0.40%和0.38%；在R10 风荷载作用下，增量分别为0.39%、0.41%和0.36%；在R50 风荷载作用下，增量分别为0.38%、0.41%和0.36%。相较风荷载强度，结构最大层间位移角随地震动强度变化更显著，故其主要受地震动强度控制。

表5 为地震-风耦合作用下结构层间变形集中系数(drift concentration factor，DCF)均值，DCF定义为：

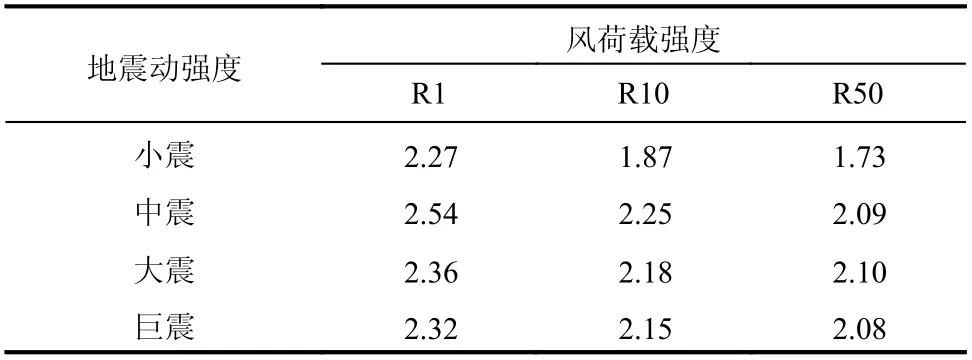
表5 结构层间变形集中系数均值Table 5 Average values of structural interstorey drift concentration factor

式中： θmax为结构各层层间位移角的最大值；ur为结构顶点位移；H为结构总高度。DCF 越大，表示结构层间变形越集中。

在小震、中震、大震和巨震单独作用下，结构DCF 分别为2.62、2.56、2.38 和2.43。由表5 可知，地震-风耦合作用下结构层间变形集中程度较相同地震动强度单独作用下更小，且风荷载强度越大，结构层间变形集中程度越小。

为研究PS-SCED 支撑在结构中发挥的控制作用，提取了PGA 为4 m/s2和5.88 m/s2的GM2 地震动分别耦合R1 和R50 风荷载作用下，结构最大层间位移所在楼层的PS-SCED 支撑滞回曲线，如图8 所示，其中，支撑1 主要承担拉力，支撑2主要承担压力，支撑1 和支撑2 在结构中的位置示于图1。可见，PS-SCED 支撑滞回性能稳定，在发生较大变形的楼层均被成功激活并充分发挥了其耗能和复位能力，在受压和受拉时均展现出良好的滞回性能。

相比大震耦合风荷载作用，PS-SCED 支撑在巨震耦合风荷载作用下的耗能能力明显提升，支撑滞回曲线更加饱满，且风荷载强度越大，支撑耗能越多，故支撑的耗能能力随着地震动强度和风荷载强度的增大而增强，并且以支撑1、支撑2为代表的对称布置于结构中的各组支撑协同工作，灵活提供抗压或抗拉能力，耗散从各个方向输入结构的能量。

3.2 结构耗能分配与残余变形

中震、大震和巨震在单独作用及耦合风荷载作用下结构的耗能分配及PS-SCED 支撑耗能占结构总耗能的比例如图9 所示。可以看出，地震-风耦合作用下输入结构的总能量随着地震动强度和风荷载强度的增大而增多，地震耦合R1 风荷载作用下支撑的耗能占比小于地震单独作用下的结果，当风荷载增强到R10 和R50，支撑的耗能能力也随之增强，地震-风耦合作用下支撑的耗能占比随之增大并超过地震单独作用下的结果。

PGA 为1.96 m/s2时，地震单独作用下仅部分支撑被激活，其耗能占比较小，为40.94%；地震耦合R1 和R10 风荷载作用时，支撑耗能占比分别为37.65%和49.84%，此时，梁柱仍为主要耗能构件；当风荷载进一步增大到R50，地震-风耦合作用下支撑耗能占比为58.66%，成为主要耗能构件。

PGA 为4 m/s2和5.88 m/s2时，地震单独作用和地震-风耦合作用下支撑耗能占比均超过80%，支撑消耗了绝大部分输入结构的能量。

PS-SCED 支撑在地震-风耦合作用下充分发挥了耗能能力，随着输入结构的能量增多，支撑逐渐成为主要耗能构件，有效保证了主体结构的安全。

残余变形反映了结构在灾后的损伤程度，是衡量结构灾后修复能力的重要指标，由图8 可见，即使在加载过程中存在较大变形，PS-SCED 支撑最终仍能基本复位至初始位置，具有良好的复位能力。

该结构在小震单独作用及小震-风耦合作用下无残余变形。中震、大震和巨震单独作用及耦合风荷载作用下结构各层最大残余变形角均值如图10所示。地震单独作用及耦合R1、R10 和R50 风荷载作用下，PGA 为1.96 m/s2时，结构最大残余变形角分别为0.008%、0.004%、0.006%和0.007%，地震单独作用时结构最大残余变形角最大；PGA为4 m/s2时，结构最大残余变形角分别为0.013%、0.012%、0.020%和0.028%，地震耦合R10、R50风荷载作用下结构最大残余变形角均大于地震单独作用下的结果；PGA 为5.88 m/s2时，结构最大残余变形角分别为0.040%、0.045%、0.059%和0.072%，地震-风耦合作用下结构最大残余变形角大于地震单独作用下的结果，且随着风荷载强度的增大而增大。风荷载为R50，PGA 为1.96 m/s2、4 m/s2和5.88 m/s2时，地震-风耦合作用下结构最大残余变形角相较地震单独作用下的增量分别为-0.001%、0.015%和0.032%。可见，风荷载对结构残余变形的影响随着PGA 的增大而越发显著。

参考类似自复位结构在四水准下的性能指标[15]，钢框架-PS-SCED 支撑筒结构在第二和第三水准对应的地震单独作用及地震-风耦合作用下的残余变形角小于0.2%和0.5%，均满足限值要求，可见，PS-SCED 支撑凭借其良好的复位能力，有效减小了结构在地震-风耦合作用下的残余变形，降低了结构的灾后损伤。

3.3 结构剪力分布与加速度放大系数

表6 为地震-风耦合作用下结构的最大基底剪力均值。在相同地震动强度下，结构最大基底剪力随风荷载强度的增大而增大；在相同风荷载强度下，结构最大基底剪力随地震动强度的增大而增大。在小震、中震、大震和巨震单独作用下，结构最大基底剪力分别为10 416.2 kN、23 184.5 kN、30 563.0 kN、38 843.5 kN；在R1、R10 和R50 的风荷载单独作用下，结构最大基底剪力分别为1684.1 kN、5147.0 kN、7637.4 kN。除巨震耦合R1 风荷载作用下结构最大基底剪力小于地震单独作用下的结果之外，其余地震-风耦合作用下结构最大基底剪力均大于地震和风荷载单独作用下的结果，但小于二者之和。

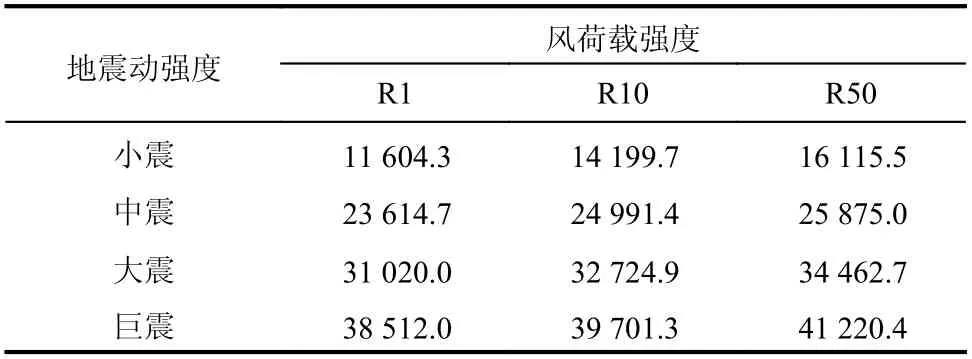
表6 结构最大基底剪力均值 /kNTable 6 Average values of structural maximum base shear force

风荷载为R50，PGA 为0.7 m/s2、1.96 m/s2、4 m/s2和5.88 m/s2时，地震-风耦合作用下结构最大基底剪力相较地震单独作用下的增幅分别为54.7%、11.6%、12.8%和6.1%。可见，地震-风耦合作用下结构最大基底剪力相较地震单独作用下的增幅随PGA 的增大呈减小趋势，PGA 越小，风荷载作用对结构基底剪力影响越显著。

图11 为小震、中震和大震单独作用及耦合风荷载作用下结构各层PS-SCED 支撑筒所承担剪力占各层总剪力的比例。PGA 为0.7 m/s2和1.96 m/s2时，结构除顶层外其余各层支撑筒均承担大部分剪力，结构下部支撑筒剪力占比较上部支撑筒剪力占比更大；地震-风耦合作用减小了支撑筒剪力占比，且风荷载强度越大，支撑筒承担剪力占比越小。PGA 为4 m/s2时，结构下部支撑筒剪力占比减小，上部支撑筒剪力占比增大，风荷载作用对结构顶层之外其余各层支撑筒剪力占比影响较小。

高层建筑对风荷载较为敏感，且楼层越高，加速度响应通常越大，人员容易出现不适，非结构构件更易损坏。图12 为小震、中震和大震单独作用及耦合风荷载作用下结构加速度放大系数均值，其中加速度放大系数即结构各层最大楼面加速度与PGA 之比。可见，PGA 为0.7 m/s2时，地震耦合R1 风荷载及耦合R10 风荷载作用下结构加速度放大系数曲线与地震单独作用下的曲线基本吻合，地震耦合R50 风荷载作用下仅部分楼层的加速度放大系数略有增大。PGA 为1.96 m/s2和4 m/s2时，地震-风耦合作用与地震单独作用下结构各层加速度放大系数差异显著，整体曲线形状呈较大改变。