基于混合策略改进的贪心算法PSS订单调度研究

任春慧

（上海工程技术大学 管理学院，上海 201620）

0 引言

随着现代化经济的发展，市场同类型产品的竞争不断加剧，如何在更好地满足客户的个性化需求的条件下，降低生产成本，提高资源的利用率和减少环境污染，将制造业向绿色智能、服务信息化转型升级，是许多企业现在及未来的发展方向。

在当今社会服务化生产的模式下，制造生产型企业把产品和服务相结合提出产品服务系统（Product Service System，PSS）。对于PSS的研究，Bu等人创建VR平台将收集并处理用户生成的数据和VR系统生成的数据，实现VR辅助的用户体验和实时数据反馈的增值服务。Mariusz等人改变PSS原有的基于销售和产品所有权从制造商转移到用户的商业模式，允许销售产品提供的可访问性和功能，为印刷行业提供更大发展空间。Kang等人在物流行业采用PSS的基础上定义和阐述了LPSS，提出了多单位维克拍卖和单面Vickrey-Clarke-Groves（O-VCG）组合拍卖并研究了对应的相关属性，包括激励相容性、分配效率、预算平衡和个人理性。Zhang等人提出了一个基于设计中心复杂性（DCC）理论的可持续PSS开发框架，采用DCC理论确定系统的复杂性类型，结合TRIZ子域模型对问题进行转换和求解并建立泛函周期性，降低系统复杂度，保持系统的长期运行稳定性。Haber等人通过Kano模型增强了PSS质量功能部署方法以筛选客户需求并将有吸引力的需求转化为接收器状态参数，将模糊层次分析法集成到该过程中评估这些参数及其固有的不确定性。Li等人针对存在个性化需求的客户，设计了块结构的马尔可夫链优化模型，较好地解决PSS问题。上述文献均对生产服务调度的运营及其管理模式进行了探讨并具有可参考价值，但并未提及到同时间大量PSS订单的调度问题，究其根源性问题是如何协调PSS订单的制造生产和满足客户的服务需求，达到服务效率和效果最优化。

为此，本文将研究产品服务系统订单调度问题，以一家有多条生产线和多支安装团队的服务型制造企业为研究对象，在满足客户个性化需求的同时，寻求订单交付时间的最小化，构建数学模型，基于贪心算法求解问题，最后仿真实验验证。

1 问题描述

假设面向市场服务型制造企业｛1，2，…，｝，拥有条生产线和支安装团队，需要满足客户的PSS订单需求，如图1所示。从规划期开始即在零点，企业接到一组订单，其中包括来自个PSS订单的订单集｛1，2，…，｝。 在这种情况下，每个订单包含一个产品单元和相应的安装服务，并指定客户要求的第一个授权服务时间，在此之前，客户由于各种原因（如缺乏安装条件）无法获得服务。

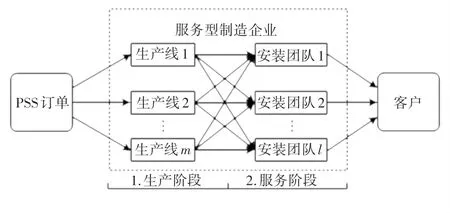
图1 PSS订单交付流程Fig.1 PSS order delivery process

PSS订单调度问题的研究重点是协调生产与服务之间的平衡，寻求最优的调度方案。对于服务型制造产业，因为产品和服务之间存在时间上的差异，服务需要以产品为媒介得到体现，且两者之间存在相互约束，所以如何协同规划生产调度已然成为亟需解决的研究课题。

2 生产服务模型

2.1 模型假设

（1）订单的生产和服务时间确定且已知。

（2）不同生产线上生产同一订单的时间相等，且不同安装队伍的服务时间也相同。

（3）每个生产线和安装队伍不能同时生产和服务不同任务。

（4）生产和服务任务都能完成。

2.2 数学模型

首先，定义以下符号和变量：

，为订单编号；为生产线（安装团队）编号；为生产阶段；为服务阶段；pt表示订单的生产时间；st表示订单的服务时间；e为订单的最早授权服务时间；表示足够大的正数；STP为订单的生产开始时间，CTP为订单的生产结束时间；STS为订单的服务开始时间；CTS为订单的服务结束时间；y表示订单的任务分配给生产线（安装团队），则y＝1，否则，y＝0；x表示订单的任务分配给生产线（安装团队），且订单早于订单，则x＝1；否则，x＝0；

PSS订单调度问题的数学模型如下：

（1）为得到订单最小交付时间的总和，目标函数为：

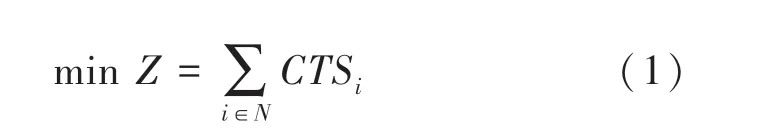
（2）在生产产品时，过程不能被打断、即不间歇生产：

（3）在生产过程中，同一条生产线有且只有一项生产任务在执行：

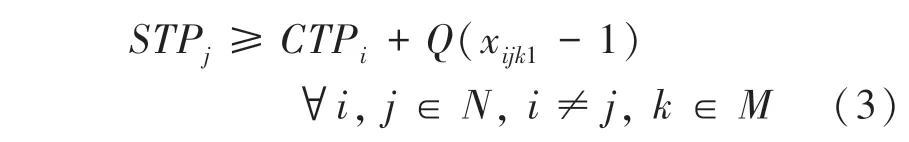
（4）生产的开始时间不能早于结束时间：

（5）同一订单的服务开始时间不能早于其最早授权服务时间：

（6）服务在提供过程中必须是连续不间断：

CTS＝STS＋st∀∈（6） （7）同一时刻每支安装队伍不能同时服务不同任务：

（8）每条生产线的生产任务执行次序，以及每支安装团队的服务任务执行次序：

（9）每个订单的生产任务必须被分配给一条生产线，服务任务必须被分配给一支安装团队：

（10）各决策变量的取值范围：

3 算法改进

在属于较大规模NP-hard问题的情况下，需要借助有效的智能算法求解模型。迭代贪心算法（Iterated Greedy，IG）是Ruiz等人提出的一种新型智能优化算法，该算法主要由邻域搜索、扰动算子和接受准则三个基本部分组成。IG算法被提出后，因其便于实现、效率高而受到国内外学者的关注和研究，并已广泛应用于约束车间流水调度、传感器网络覆盖增强问题研究等领域。

本文提出了一种混合策略改进的IG算法，可以用来求解PSS订单调度问题。首先，对订单进行排序，然后初始化订单序列，运用改进的邻域搜索，迭代寻找最优解并不断替换，再对扰动算子重新进行破坏和重建，防止过早收敛。最后，根据轮盘赌设计出一套新的接受准则更新最优解，直到算法运行结束。

3.1 初始化

本文利用Nawaz-Enscore-Ham（NEH）算法对IG初始化加以改进，通过NEH算法对所研究的订单最早授权服务时间重新进行排序，获得一个数列。首先选择数列中时间之和较短的前2个订单调度为基本序列，然后其他订单分别调入基本序列，选择最短时间和的序列为新的基本序列，接着重复以上步骤并不断调整基本序列，最后会获得一个新的数列。

3.2 邻域搜索

本文为增强IG算法的寻优能力，根据随机搜索和交换邻域的思想，提出一种随机邻域搜索（Random Neighborhood Search，RNS）算法，其思路主要如下：每次在当前解之中随机选取一个个体，而后再随机插入其任何可能最优预测的区域，或者将个体与最优位置的个体进行位置互换，一旦新解优于原解，则保留新解并重复上述过程、直至不再生成较高解。这个方式能够大幅增加搜寻的范围并提高寻优效果。

3.3 破坏与重建

为了避免IG算法在求解过程中陷入局部最优，需要对其运行过程进行破坏与重建、跳出原有机制，又称为扰动算子。原始IG算法的扰动算子在发生作用之后，可能会发生丢失局部最优解的情况，为此本文 提 出 一 种 结 合 破 坏（Destruction）、优 化（Optimization）和重建（Construction）过程（DOC）作为改进IG算法的扰动算子，其操作过程如下：在实施破坏过程后，将得到的解重新进行多次邻域搜索得到优化解，此后再对其进行重建，提升了扰动解的优良性。

3.4 阈值接受准则

为实现IG算法更快找出最好解这一目的，本文提出一种基于轮盘赌选择（Roulette Wheel Selection，RWS）策略的接受准则。根据求解问题的特点，设计一个优选表，在优选表中依次添加局部搜索产生的较优解，当达到表的最大长度时删除表中原有最差解，最后利用RWS选择表中解。设置优选表长（≤），对RWS选择策略步骤可给出阐释分述如下。

对优选表中的解进行归一化处理：

步骤3 在［0，1］中选择随机数。 如果，则选择优选表中第一个解；否则，选择表中第个解，使得q≤Rand＜q成立。

3.5 终止条件

考虑到问题规模，保证算法充分收敛，本文设置改进IG算法的终止条件为10*ms。

3.6 算法流程

研发后得到的整个算法的求解流程具体如下。

4 仿真实验

4.1 算例构造与性能评价指标

本文从测试集合中随机选择测试算例。设置pt和st由区间1，100[ ]的均匀分布随机产生，e由区间［pt，（1）pt］均匀分布随机产生。实验中关键参数的取值从108种参数集合中选取，｛50，100，150，200｝、｛2，5，10｝、｛2，3，5｝和｛1，2，3｝。 每个参数序列随机产生2个算例，最后可形成216个基准测试集合。

使用相对偏差指数（relative deviation index，）评价IG的能力：

4.2 实验参数设置

设置50个算例，每个算例通过选择｛20，50，80，100，120，150，180，200｝以及、和集合中随机值。MIG算法主要测试和，设置：｛1，2，3，4｝和｛5，6，7，8｝。测试结果分别取运行5次后的平均值。

运用双因素方差分析所得结果，见表1。当值比0.05小的时候，代表着对应因子的影响显著。由表1可见，对MIG影响显著，而对MIG则表现出较为明显的影响性。并且在和同时产生作用的情况下，对MIG的性能影响也不明显。

表1 MIG算法参数设置实验的ANOVA结果Tab.1 ANOVA results of MIG algorithm parameters setting experiment

为进一步研究和对MIG算法的影响，对参数选取不同值得到均值和95%LSD置信区间，如图2所示。由图2可以看出，MIG的性能随着的增大而下降，而对MIG的影响并不显著。取1，6。

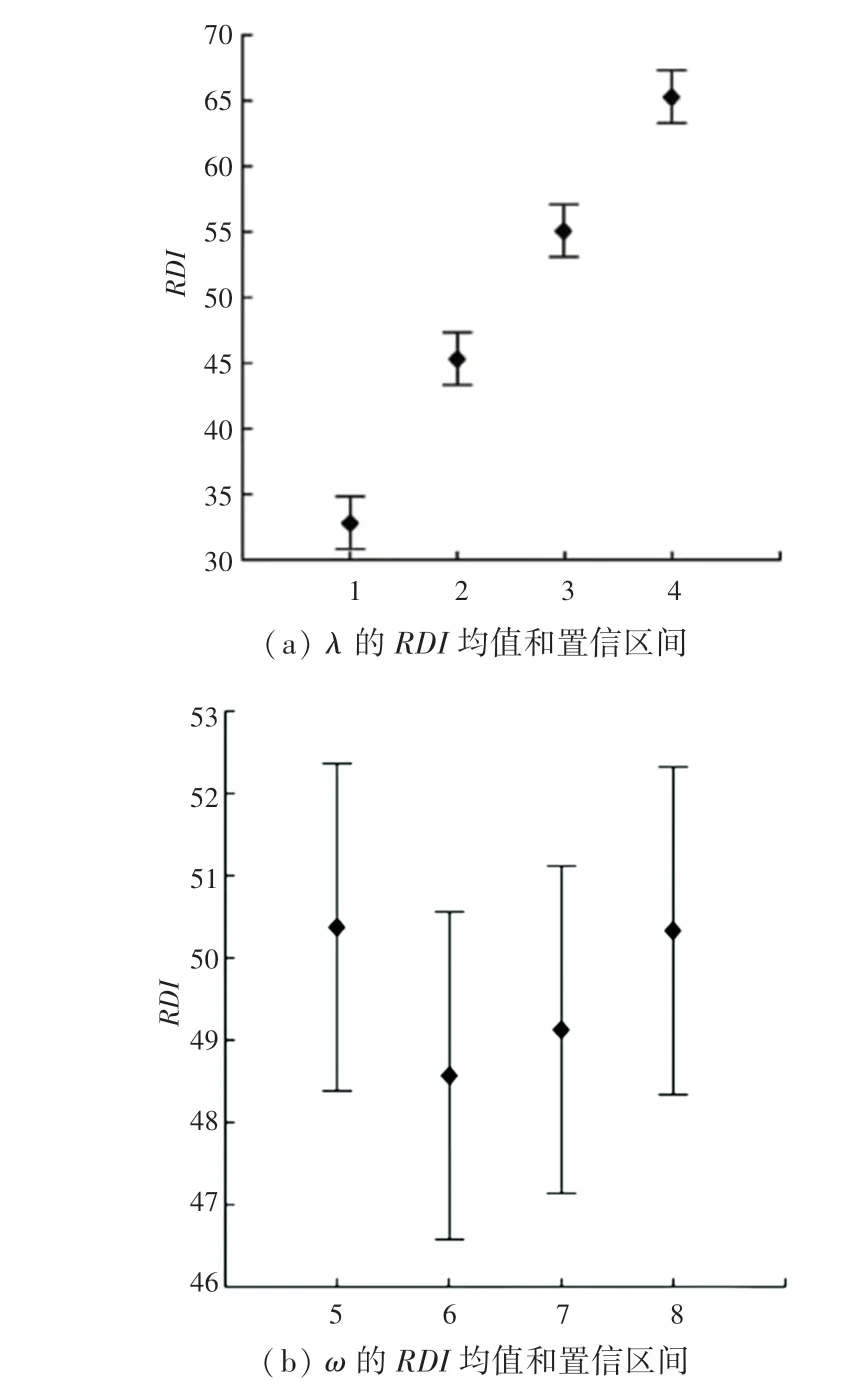
图2 λ和ω分别取不同值时改进IG算法置信区间Fig.2 Improved confidence interval of IG algorithm when λ and ω take different values respectively

4.3 有效性与鲁棒性分析

将混合策略改进的贪心算法分别与经典IG算法、随机邻域改进的贪心算法（IGRNS）、扰动算子改进的贪心算法（IGDOC）、轮盘赌改进接受策略的贪心算法（IGRWS）进行对比实验，分别测试不同改进策略效果。

IG算法改进的RDI均值和95% LSD置信区间图如图3所示。由图3可以看出本文提出的改进策略对于提升贪心算法的性能均是有效的，MIG效果最为明显，值优于IG约为84%。同时，IGRNS的值优于IG算法约35%，IGDOC的值优于IG算法约58%，IGRW算法的值优于IG算法约5%，明显地，破坏重建过程中的扰动算子对算法性能的影响最为显著。

图3 IG算法改进的RDI值Fig.3 Improved RDI value of IG algorithm

MIG算法对求解算例中的具有关键性作用的参数敏感性变化趋势如图4～图7所示。

由图4可以看出，随着的增加，MIG的均值呈现明显的减小，而IG的均值持续上涨，这反映了MIG算法对于求解更加庞大、及复杂调度类型问题的效果会更为准确。由图5和图6可见，MIG的值几乎不随着和的增加而波动，这反映了生产产品的流水线数量和安装团队数量的增加几乎不会降低MIG算法性能，反映了MIG对和的鲁棒性能较优。在图7中，随着的增大，各订单的最早授权服务时间就越分散，并同样反映出MIG较优的鲁棒性。

图4 MIG关于n的变化趋势Fig.4 Variation trend of MIG on n

图5 MIG关于l的变化趋势Fig.5 Variation trend of MIG on l

图6 MIG关于m的变化趋势Fig.6 Variation trend of MIG on m

图7 MIG关于θ的变化趋势Fig.7 Variation trend of MIG on θ

5 结束语

本文面向具有数条产品生产流水线和安装队伍的生产服务型企业，可以为客户推荐较为合适的订单交货前的最早授权服务日期，减少不必要的等待时间，寻求最短交货时间，建立了标准数学模型，并针对PSS订单调度问题特点设计了求解问题的混合策略改进IG算法。通过仿真测试，证明了IG算法改进策略的有效性和鲁棒性。本文提出的PSS订单调度模型及IG算法混合改进策略求解方法可以为企业决策提供有效的决策建议，为消费者提高服务水平降低成本。在未来的研究中可以将本文方法推广到汽车制造，交通调度等行业中。