螺杆挤压-旋转式磁流变阻尼器力学特性研究*

2022-11-04曾泽璀张磊闫明董小闵

振动、测试与诊断 2022年5期

关键词：剪切力阻尼器角速度

曾泽璀，张磊，闫明，董小闵

（1.沈阳工业大学机械工程学院沈阳，110870）

（2.海军研究院北京，100161）

（3.重庆大学机械传动国家重点实验室重庆，400044）

引言

随着智能控制技术和智能结构或材料的发展，给复杂结构在各种复杂振动冲击环境下的振动响应抑制带来了契机。Zhu等［1］对传统的磁流变阻尼器结构设计以及应用状况进行了概述。以磁流变材料为代表的智能材料在众多工程应用领域得到了广泛的应用，其具有响应速度快、可重复性高及动态范围广的特点［2-4］。根据不同的应用场合，可以选择相应的磁流变阻尼器的工作模式来匹配，从而提高磁流变阻尼器的工作效率［5-6］。为了能够准确描述磁流变阻尼器的力学特性，需要建立准确的模型。常用于描述磁流变阻尼器准静态特性的本构模型主要包括Bingham模型和Herschel-Bulkley模型［7-8］，其中Herschel-Bulkley模型能够反映流体的剪切稀化特性和剪切稠化特性，因此该模型也被经常用于磁流变阻尼器的建模当中［9］。

传统的剪切式磁流变阻尼器结构形式有限，一般其所产生的阻尼力与驱动速度相关，均体现出黏性阻尼特征［10］。为增加剪切磁流变阻尼器的有效输出阻尼，通过增加结构尺寸是一个有效的方法［11］。Imaduddin等［12］总结了传统旋转式磁流变阻尼器的结构形式，并描述了大量的混合式旋转磁流变阻尼器结构及其应用领域。

近年来，许多专家学者为了进一步研究磁流变液体的特性，对许多混合模式下的磁流变阻尼器进行了研究，从而为提高阻尼力矩寻求物理依据［13］。Dong等［14］研究了轴向挤压对磁流变阻尼器的影响，发现通过适当增加轴向挤压压力能够提高阻尼器的阻尼力矩。文献［15］将螺旋结构应用于磁流变阻尼器中，研究了磁流变液体在螺旋流动状态下的力学特性。于建强［16］基于螺杆结构设计了一种新型的磁流变阻尼器，发现该结构下的磁流变阻尼器与传统剪切式旋转阻尼器相比在性能上有所提升。Yu等［17］对螺旋式磁流变阻尼器进行了参数优化设计，并通过试验证明该阻尼器具有较高的阻尼力矩输出效率。上述研究说明通过改进结构能够提高磁流变阻尼器在有限空间内的阻尼力矩，但是阻尼器仍然表现出黏性阻尼特征。在实际工程应用中，库伦阻尼不仅能够有效地消耗系统能量，而且其与速度之间无直接相关，能够在保证加速度响应较小的情况下，最大限度地耗散系统能量，相对黏性阻尼具有一定的优势。因此，获得具有库伦阻尼特征的磁流变阻尼器具有十分重要的意义。与传统的阻尼器结构相比，基于螺杆挤压的SR-MRD能够有效地提高阻尼器的阻尼力矩，降低阻尼器阻尼力矩与扭转角速度之间的相关性。因此，本研究提出具有大尺寸的SR-MRD结构来获得阻尼器的库伦阻尼特征。

1 SR-MRD阻尼器结构原理

传统的磁流变阻尼器主要有3种工作模式，分别为流动式、剪切式和挤压式，如图1所示［1］。研究人员为了提升磁流变阻尼器的极限性能，对磁流变阻尼器传统的工作模式进行混合，从而演变出流动-剪切、挤压-剪切等混合模式。

图1 传统磁流变阻尼器工作模式Fig.1 Working mode of traditional MRD

笔者所研究的SR-MRD属于流动模式和剪切模式的组合。在SR-MRD中磁流变液体的流动方向与剪切运动方向夹角为90°，其既不同于传统的3种工作模式，也不同于常见的混合模式。SR-MRD工作原理如图2所示。该阻尼器是委托重庆大学加工的定制产品。

由图2可知，SR-MRD由螺杆、定子、转子、阻尼器外缸及通电线圈组成，在SR-MRD中一共含有3个流动通道。定子和阻尼器外缸与基座连接固定不发生转动，其中定子含有2个线圈槽，当槽内的线圈通电，定子就会产生磁场影响通道2和通道3中的磁流变液体。螺杆与转子相连接，可以相对定子和阻尼器外缸转动，二者同步转动和停止，具有相同的角速度。

图2 SR-MRD工作原理Fig.2 Working principle of SR-MRD

当螺杆发生转动时，螺杆将推动螺杆腔内的磁流变液体流动，并且通过通道2和通道3发生流动，因此在通道2和通道3两侧存在一定的压强差，该压强差会产生一定的阻尼力矩。另外，当转子与定子发生相对转动时，通道2和通道3中的磁流变液体将发生周向剪切作用，从而产生一定的剪切阻尼力。因此，SR-MRD的阻尼力矩主要受到剪切力和压强差的影响，这一工作原理与传统磁流变阻尼器不同，如图3所示。

图3 磁流变阻尼器工作模式对比Fig.3 Comparison chart of working mode of MRD

图3（a）为传统的阀式磁流变阻尼器工作模式，其流动剪切力方向与平板运动剪切力方向相反，二者力的方向夹角为180°；图3（b）为SR-MRD工作模式，其运动平板移动方向与轴向压差方向间的夹角为90°。由于受到周向相对转动和轴向挤压的影响，通道2和通道3中的流体受到2个驱动力的作用：①由压强差所产生的轴向驱动力；②由周向剪切力产生的周向驱动力。所以，SR-MRD内液体的实际流动方向为图4所示的M方向，其剪切力分布情况如图5所示。

图4 SR-MRD液体流动方向Fig.4 Flowing direction of SR-MRD fluid

图5 磁流变液体剪切合力Fig.5 Shear force analysis of MRD

由图4可知，SR-MRD具有2个方向上的作用力，其产生的原因如下：①由于间隙通道两端的压力差所引起的x方向（轴向）上的液体流动；②由于定子与转子之间的相对转动所引起的y方向（周向）的剪切运动。在这2个力的耦合作用下，磁流变液体的实际流动方向为M方向，其流动速度为

图5中，紫色线为剪切模式所产生的应力分布，红色线为流动模式所产生的应力分布。由图5（a）可见，阀式磁流变阻尼器的剪切模式与流动模式所产生的剪切力平行于同一轴线，二者的剪切力合力可以近似为线性叠加；由图5（b）可见，剪切模式与流动模式所产生的剪切力夹角为90°，因此二者的剪切合力为

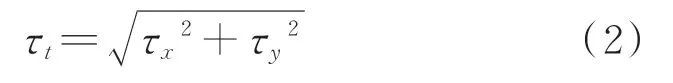
传统阀式阻尼器的剪切合力为

通过对比式（2）和式（3），可以发现当阻尼器中流体的流动模式和剪切模式所对应的剪切力为固定值时，SR-MRD的剪切合力要大于传统阻尼器，即

其中：剪切力的符号均为正值。

值得注意的是，同一种磁流变液体，在相同的磁场强度下，其屈服强度相同。因此，与传统的旋转式磁流变阻尼器相比，SR-MRD所产生的剪切合力更大，能够更容易达到剪切屈服状态并且保持恒定的阻尼力。这为SR-MRD的库伦阻尼特征提供了物理基础。

2 动力力学模型

在SR-MRD工作过程中，通道2和通道3内的工作模式为混合模式，即剪切模式和流动模式的组合。针对螺旋式扭转磁流变阻尼器，已有专家学者利用Bingham模型进行建模并分析阻尼特性［17］。考虑到磁流变液体的剪切稀化特性，笔者利用Herschel-Bulkley模型对SR-MRD进行建模并分析其阻尼器特性。

2.1 SR-MRD流量计算

当SR-MRD逆时针转动时，其液体流动方向为图2所示的红色箭头方向；当顺时针转动时，液体流动方向与其相反。由于SR-MRD在顺时针与逆时针转动工作条件下所产生的阻尼力矩效果基本相同，因此这里以逆时针转动的工作情况为例，对其进行说明。当螺旋杆逆时针转动时通道1分为2个腔，1个挤压腔和1个吸入腔。为了简化计算，假设螺杆每转动1圈所吸入和排出的液体体积相同，且与螺杆参数相关，包括：螺旋升角θ、导程L、大径R1、小径R2、齿间距b及齿高hc。当螺旋杆转动1周、其扭转角为360°时，则轴向推进距离为导程L=nS，其中：n为螺旋头数；S为螺距。由于所采用的螺杆为单头螺杆，则n=1。因此，螺旋杆转动1周所输送的流量体积为

流量与旋转角速度的关系为

SR-MRD在外部阻尼力矩的作用下，当扭转角速度为w时，就有对应的Q(w)经过通道2和通道3。

2.2 流体力学分析

由于通道2和通道3区别在于磁场强度以及通道半径不同，这里以通道2为例，对该通道内的液体流动速度以及压强差剪切力情况进行计算，通道3的相关力学模型可以同理类推。笔者考虑磁流变液体的剪切稀化动态力学特性，利用Herschel-Bulkley模型［18］来描述

其中：τ0为屈服应力（与磁场强度有关）；H为磁场强度；˙为剪切应变率；m为剪切稀化因子；K为流体黏度。

由于该模型考虑了磁流变液体的剪切稀化效应，当m=1时，即可变为Bingham模型。对于具有流动特性的磁流变阻尼器，磁流变液体的剪应力和沿液体流动方向上的压力梯度满足Navier-Stokes方程，即

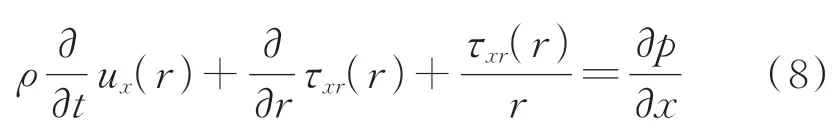
其中：ux(r)为流速；τxr(r)为剪应力；r为径向坐标；x为轴向坐标；ρ为液体密度；∂p/∂x为压力梯度。

在SR-MRD中，由于通道2与通道3的半径要远大于通道间隙，因此笔者考虑利用平板模型进行计算。但是为了方便获得阻尼器参数对阻尼力的影响趋势，在本分析中对流体的力学分析过程进行简化处理。假设忽略液体流动的惯性力，则式（8）可简化为

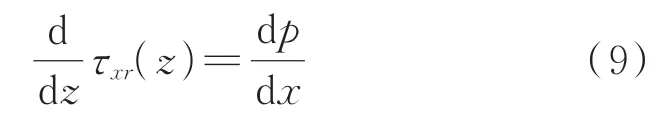
式（9）的解为

其中：D1为求解微分方程过程中所产生的常数。

图6为SR-MRD的速度分布。沿轴向发生的液体流动是发生在2个固定平板之间，且在2个平板的输入与输出口之间存在压力差，如图6（a）所示。由于定子与转子之间相对转动，因此在周向发生的液体流动是由于2个相对移动的平板所引起的，如图6（b）所示。

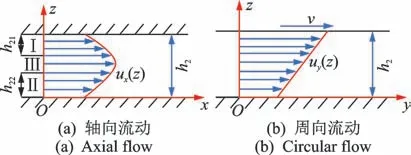
图6 SR-MRD速度分布Fig.6 Velocity distribution of SR-MRD

在SR-MRD中，其液体流动模式由轴向流动和周向流动产生，因此在本研究中先将二者分开独立计算，然后再计算液体耦合流动速度。首先，假设阻尼器的定子与转子之间不发生相对转动，则此时的磁流变液体在2个平板之间沿x方向平稳流动。基于Herschel-Bulkley模型考虑磁流变液体的剪切稀化效应，如图6（a）所示，在区域Ⅰ中，剪切应变率γ˙=dux/dr≥0，在该区域内流体的剪切力为

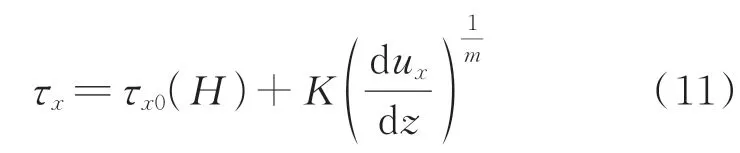
将式（11）代入简化Navier-Stokes方程解中，由于2个平板均为固定，因此边界条件为：ux(0)=ux(h)=0。则在区域Ⅰ中，磁流变液体的流动速度为

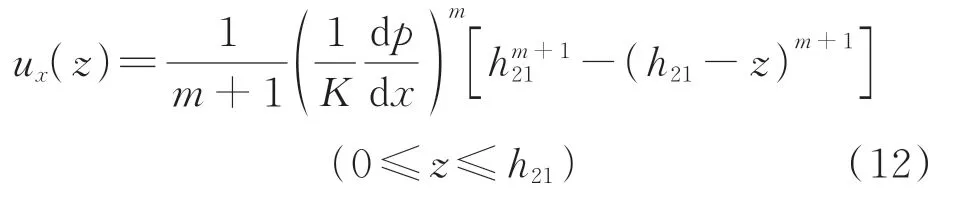
在区域Ⅱ中，磁流变液体的流动速度为

在“核心区域”（区域Ⅲ）边界流速ux(h1)=ux(h2)，则由式（12）和式（13）可得

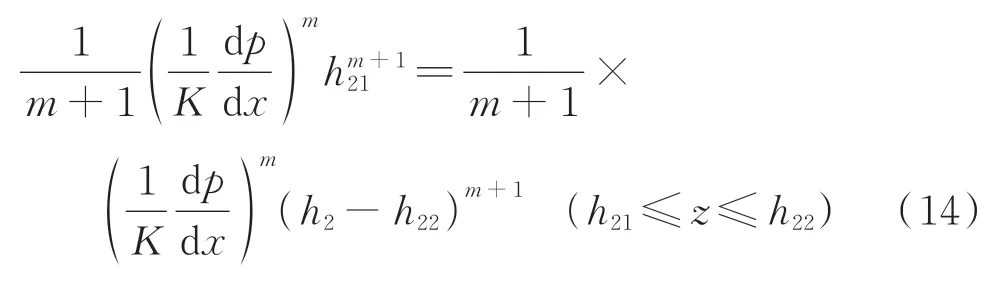
通过化简可得，h21=h2-h22。因此，对于两固定平板的流动模式，“核心区域”的高度为0。将速度梯度对高度h进行积分获得阻尼器通道2内的流量

其中：h21和h22分别为通道2内区域Ⅰ和区域Ⅱ的高度；h2为通道2总高度；W2为通道2的宽度。

根据积分可以获得

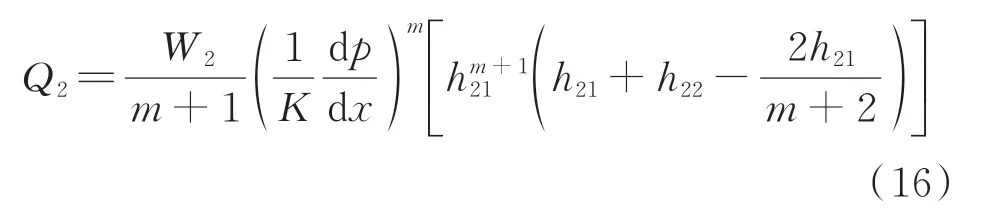
同理通道3的流量Q3为

其中：h31和h32分别为通道3内区域Ⅰ和区域Ⅱ的高度；W3为通道3的宽度。

由上述2个通道的流量表达式，可以获得阻尼器的总流量为假设在流动模式下，通道2和3中的流体不受轴向平行板运动的影响，其流动区域可以分为Ⅰ和Ⅱ，而且区域Ⅲ高度为0，因此h21=h22。在本模型中，通道2与通道3的间隙相同：h21=h22=h32=h31。由于通道2和通道3两端的压强差相同，不同的是平板的宽度，因此通道2和3的总流量简化为联合式（6）和式（19），可以求出SR-MRD压力差为

由式（20）可以看出，压强差与黏度呈正相关关系，其主要受到螺杆参数、通道间隙、加速度及剪切稀化因子m的影响。根据式（20），计算各主要参数对压强差的影响规律，如图7所示。

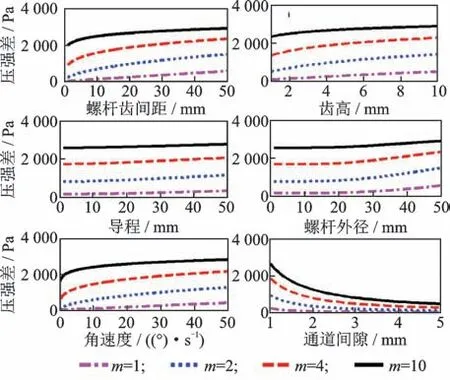
图7 结构参数对SR-MRD压强差的影响规律Fig.7 The effects of structural parameter onΔP of SR-MRD

由图可以看出，压强差与主要螺杆参数和角速度均呈正相关关系，螺杆外径、齿高、齿间距及角速度对压强差的影响程度都要大于导程；与此相反，增加通道间隙会降低SR-MRD内部压强差。当SR-MRD考虑磁流变液体的剪切稀化效应时，随着剪切稀化因子m的增加，螺杆齿间隙、齿高、导程及外径变化对压强差的影响都会随之降低，但是整体压强差数值随着m的增加而提高。

2.3 剪切力计算

SR-MRD的剪切模式主要是由通道2和通道3内部的剪切运动产生，这里以通道2为例进行计算。假设下板固定不动，上板以v的速度进行移动，线速度等于角速度乘以半径（v=wr）。为了简化计算，假设在剪切模式下，仅有平行板移动，两侧无压强差，且剪切应力分布为线性分布，则其所产生的阻尼力为

其中：L为通道2的长度；R21为通道2的内径；R22为通道2的外径；τz0(H)为通道2内磁流变液体的剪切屈服强度，其关于磁场强度的表达式参考文献［19］。

由式（21）可以看出，阻尼力与磁场H、角速度w以及通道面积W2L相关。通道3的阻尼力同理求得。

2.4 阻尼力矩计算

根据上述所推导的压强差以及剪切阻尼力计算公式，可进一步推导出SR-MRD所产生的阻尼力矩。由压强差所产生的阻尼力矩由2个部分组成：①由于螺杆两侧压强差所引起的周向推力分量造成的阻尼力矩；②由轴向推力分量所引起的密封圈摩擦阻尼力矩。

图8为螺杆受力分析图。由图可见，在有效接触面积A上所产生的压力为

图8 螺杆受力分析Fig.8 Force analysis of screw structure

其中：A为螺杆有效接触面积，L1为单圈螺旋线长度。

该压力所对应的轴向分力以及周向分力分别为

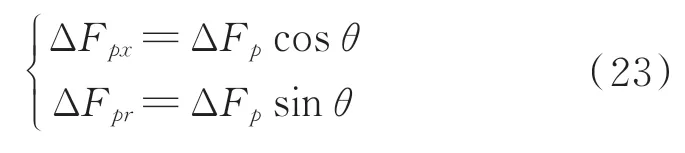
由于轴向力是直接作用在端盖支撑装置上，转化为螺杆支撑轴与密封圈之间的摩擦力ΔFm=ΔFpxμ。由摩擦力所产生的摩擦扭矩为

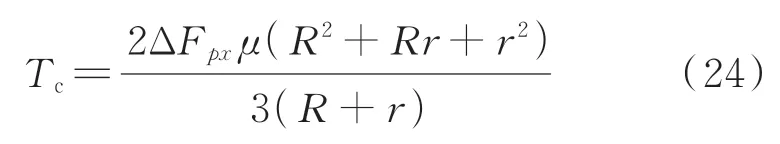
其中：μ为摩擦面间的摩擦因数；ΔFpx为摩擦面承受的单位压力；R为摩擦接触面外径；r为摩擦接触面内径。

周向力是在扭转方向产生阻尼力作用，因此将周向阻尼力矩等效为周向分力乘以中心线半径，根据式（22）得

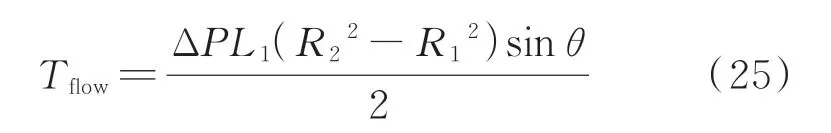
剪切稀化现象对压强差所产生的阻尼力矩的影响，如图9所示，其中上面两幅图为m对Tc和Tflow的影响规律。

图9 剪切稀化因子m对阻尼力矩的影响Fig.9 The effects of shear thinning factor m on damping torture

由图可以看出，由轴向分力所产生摩擦阻尼力矩Tc要大于螺杆周向分力所产生的阻尼力矩Tflow。而且，由于摩擦阻尼力矩受到压强差的影响较大，因此当系统结构参数不变的情况下，角速度的增加会直接导致摩擦阻尼力矩增加。除此之外，还发现剪切稀化因子m对阻尼力矩产生了较为明显的影响，主要表现在阻尼力矩对角速度的敏感程度。当剪切稀化因子m为1时，SR-MRD表现出Bingham流体特征，体现出与角速度较高的相关度，表现为黏性阻尼特征。随着剪切细化因子m的增加，当加速度越大，阻尼力矩与角速度之间的相关性降低，阻尼力矩逐渐呈现出库伦阻尼特征。

在通道2和通道3内，由定子和转子之间的相对转动所引起的阻尼力矩计算公式为

其中：T2和T3分别为通道2和通道3中由剪切力所产生的阻尼力矩；H2和H3分别为通道2和通道3中的磁场强度。

当不考虑磁场作用时，T2和T3分别如图9所示。由图可见，由通道2所产生的阻尼力矩要低于通道3，这是因为通道2的半径小于通道3所引起的。当剪切稀化因子m为1时，剪切力矩体现出与角速度较高的相关度，表现为黏性阻尼特征。随着剪切细化因子m的增加阻尼力矩与速度之间的相关性降低，阻尼力矩逐渐呈现出库伦阻尼特征。

SR-MRD产生的总阻尼力矩Ttotal由液体的流动、剪切以及固定轴与密闭件间的摩擦所决定，分别为Tflow，Tshear和Tc。其公式为

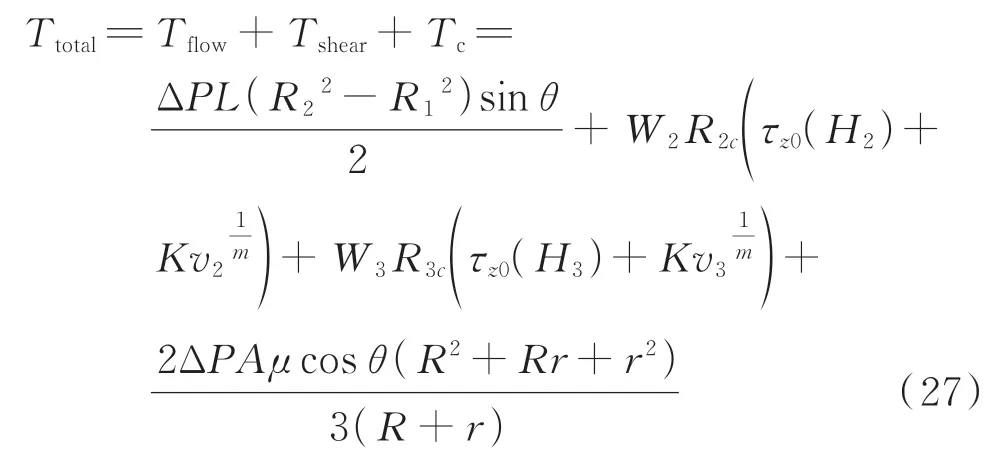
根据式（27）计算出不同磁场强度作用下的总阻尼力矩，如图10所示。

图10 线圈电流对阻尼力矩的影响Fig.10 The effects of coil current on damping torture

图10列举了5个磁场强度所对应的阻尼力矩，分别对应着线圈中电流为0，1，2，3和4 A的情况。由图可见，SR-MRD的阻尼力矩随着磁场强度的增加，呈现出上升趋势，但是由于受到磁场强度的饱和作用，在电流超过2 A之后其上升趋势开始减缓。另外，通过观察还可以发现，与Bingham流体对比，当考虑剪切稀化作用之后，SR-MRD的阻尼力矩与外界驱动角速度之间的相关性降低，并且在较大的角速度范围内呈现出显著的库伦阻尼特征。

3 阻尼力矩测试

3.1 原理样机及试验设备

根据SR-MRD结构原理，并基于Herschel-Bulkley建立流体力学模型。为了保证SR-MRD原理样机具有库伦阻尼特征，需要增加通道2和通道3的有效直径，从而促进2个通道内磁流变液体的剪切稀化效应。为了对原理样机的阻尼特性进行测试，将其安装在MTS扭转试验机上进行测试。SR-MRD原理样机及测试如图11所示。

图11 SR-MRD原理样机及测试平台Fig.11 Prototype of SR-MRD and testing platform

3.2 试验结果及分析

根据2.4节中所推导的阻尼力矩公式（27），通过分析阻尼力矩的影响参数发现，对于具有剪切稀化效应的磁流变液体而言，只有当剪切速度较大时会体现出剪切稀化效应。因此，在其他参数不变的情况下，增加通道2和通道3的有效半径会促进磁流变液体的剪切稀化程度，加快磁流变液体达到剪切屈服力。相比以往的剪切式阻尼器，本研究试验的SR-MRD的结构尺寸较大，通道2和通道3的有效半径增加，在同样的角加速度作用下，具有更高的剪切速率，从而加快了阻尼器内部剪切稀化效应，并且达到一个屈服状态，从而有利于降低阻尼力矩与角速度之间的相关性，使得SR-MRD具有库伦阻尼特征。

在测试试验过程中，通过调整MTS试验机的扭转幅值和频率来完成阻尼器阻尼力矩的测试，试验的扭转角幅值分别为10°和25°，测试频率分别为2和10 Hz。扭转试验的测试结果分别如图12和图13所示。

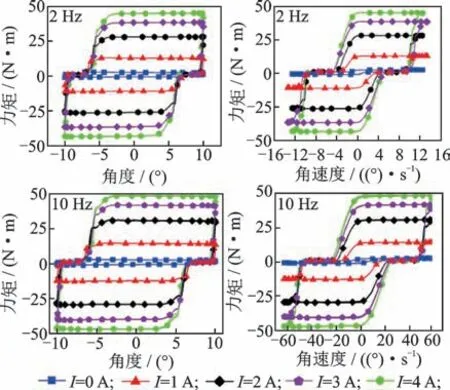
图12 幅值为10°的MTS扭转试验Fig.12 MTS test of SR-MRD with 10 degree amplitude

图13 幅值为25°的MTS扭转试验Fig.13 MTS test of SR-MRD with 25 degree amplitude

当MTS试验机以10°的幅值进行试验且频率为2 Hz时，由阻尼力矩-转角曲线可见，在大部分角度范围内，阻尼力矩保持在一定数值范围内并且基本恒定；由阻尼力矩-角速度曲线可见，除了在角速度方向发生变化时，阻尼力矩开始下降，在整个路程中，一半以上的角速度范围内都是保持在恒定值附近。

通过对比2 Hz和10 Hz试验可以看出，随着频率的增加，保持恒定阻尼力矩的角速度范围也在增加。但是由于原理样机受到加工工艺影响，使得SR-MRD存在一定的扭转间隙，因此在初始转动时，有接近3°的扭转间隙，从而造成阻尼力矩-角度试验曲线中存在一段零阻尼力矩数据。另外，在不同频率条件下，饱和阻尼力矩值主要受到磁场作用发生明显变化，当电流为1～3 A变化时，其阻尼力矩都有比较明显的增加，但是从3～4 A，其阻尼力矩增加量开始下降，这是受到磁流变液体饱和磁场的作用影响。

由图13可见，振动幅值为25°时的振动测试曲线与振动幅值为10°的响应规律基本相同。SR-MRD的阻尼力矩也是随着磁场强度的增加而增大，而且在较大的振动范围内同样呈现出较为明显的库伦阻尼特征。虽然同样受到扭转间隙的影响，但是由于扭转间隙角度固定，因此试验振幅增加仍然扩大了具有库伦阻尼特征的角度范围。

SR-MRD的振动试验结果表明，SR-MRD能够输出稳定有效的阻尼力矩，并且具有明显的库伦阻尼特征。另外，通过观察对比理论阻尼力矩-角速度曲线与试验曲线发现，理论计算结果与试验结果具有相同的趋势，SR-MRD的阻尼力矩随着磁场强度增加而增大，在较大范围内体现出库伦阻尼力的特点。