超声电机启动瞬态的电参量测试*
2022-11-04韩威季宏丽聂瑞陈虎城裘进浩
韩威,季宏丽,聂瑞,陈虎城,裘进浩
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
引言
超声电机因其具有精度高、质量轻、响应快、构型灵活、结构刚度大、断电自锁及电磁兼容性好等优点[1-2],成为航空航天[3]、医学设备[4]、机器人[5]及精确制导武器[6]等领域中精密驱动机构的主要功能部件。近年来,高端装备对超声电机提出了更为苛刻的作动需求,因此建立准确的超声电机模型,充分了解其响应特性,是促使超声电机的输出性能、定位精度、运行稳定性和服役可靠性向纵深发展的必要前提。
超声电机的模型主要包括解析模型、有限元模型和等效电路模型。由于超声电机复杂的压电耦合特性和定转子间摩擦的非线性,使其解析模型和有限元模型都存在建模困难、求解复杂及使用不便等问题[7-8]。相比之下,等效电路建模将超声电机的机械量等效为电学量,通过电学理论实现对超声电机特性的分析,是一种简洁有效的分析方法[9-11]。但是,超声电机等效电路模型电参量的确定具有后验性,需要相应测试实验的支持。
目前,国内外学者在超声电机的电参量测试方面取得了一些研究成果。魏守水等[12]提出了一种基于导纳圆的超声电机定子电参数测量方法,证明了通过导纳频率特性求取电机电学特性参数的方法具有可行性,并对定子的频率特性和电机效率之间的关系进行了分析。Li等[13]基于拉格朗日方程建立了一种非线性等效电路模型,描述了电流谐波的非线性特征,并提出了一种非线性调谐的驱动电路,抑制了超声电机的电流谐波。牛子杰等[14]提出了超声电机及驱动器组成的并联等效电路整体模型,通过电学仿真得到机电系统的阻抗特性,并通过傅里叶分解法对电机驱动电压和驱动电流信号进行处理,得到超声电机实际工作中的阻抗特性。陈宁等[15]提出了一种能对超声电机主要机电参数进行测量和控制的实验系统,该系统覆盖了超声电机主要的8项控制参数与13项状态参数,能够实现控制参数的在线精确调控与状态参数的快速测量。上述研究基于不同理论分别给出了超声电机电参量的测试方法,然而这些方法仅适用于电机在稳定运行状态下的电参量测试。瞬态测试实验表明,超声电机启动瞬态的过程中相关电参量有剧变的特点,这表明超声电机的工程应用中需要考虑启动过程中电参量变化对超声电机响应特性的影响。尤其是在精密定位等需要超声电机频繁启动的领域,测试电机启动瞬态的电参量,揭示各项电参量在启动过程中的变化规律,有助于分析超声电机的响应特性,对超声电机驱动电路的设计,完善超声电机等效电路模型具有重要意义。
首先,笔者基于短时傅里叶变换的时频分析理论,提出一种超声电机启动瞬态的电参量测试方法;其次,通过对仿真信号进行处理分析,验证该方法在启动瞬时电参量计算方面的准确性;最后,通过搭建超声电机瞬态测试系统,采集超声电机启动过程中的驱动信号,并对其进行时频分析,得到相关电参量随着超声电机启动过程的变化曲线,验证该方法在启动瞬时电参量测试上的有效性。
1 超声电机瞬态测试系统
1.1 系统组成
超声电机瞬态测试系统如图1所示。该系统由光电编码器、功率放大器、波形发生卡、高速数据采集卡、电流探头、分压电路、PXI机箱和显示器等设备组成。在测试的过程中,波形发生卡输出2路幅值、频率和相位差可调的正弦信号,经由功率放大器后输出超声电机的驱动信号。与此同时,PXI机箱控制数据采集卡采集经分压电路处理后电压信号、电流信号和光电编码器的信号,经过数据处理后将测试结果显示在屏幕上。
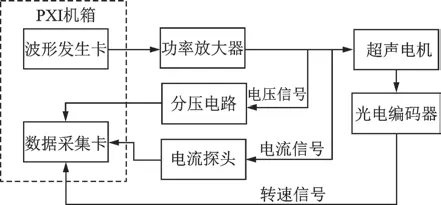
图1 超声电机瞬态测试系统Fig.1 Transient testing system of ultrasonic motor
1.2 程序设计
在超声电机的瞬态测试过程中,由于超声电机启动过程的时间在毫秒级,因此需要保证原始测试数据的丰富性和实时性。
本测试系统中的数据采集卡使用的是NI公司的PXI-5105的多通道同步数据采集卡,具有12位模拟输入分辨率,最大采样速度可达60 MS/s,其高采样率的特性可确保在短时间内采集足够多的数据,很大程度上减小信号采集的失真。另一方面,通过LabVIEW软件设置将NI-PXIe5423信号发生卡和NI-PXI5105数据采集卡共享PXI机箱内部时钟源,从而实现板卡间的同步触发以保证数据采集的实时性。此外,数据处理方面采用了Matlab Script脚本技术,将数据处理部分模块化,利用Matlab可以实现数据快速处理,简化测试流程,提升测试效率。整个测试流程如图2所示。
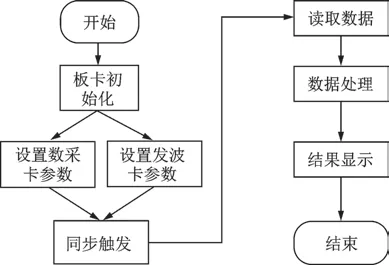
图2 超声电机电参量测试流程Fig.2 Testing process of electrical parameters of ultrasonic motor
2 超声电机启动瞬态的电参量测试方法
超声电机的电参量包括驱动电压、电流、阻抗、阻抗角、等效电阻、等效电抗和有效功率等,分析启动瞬态电参量随时间的变化规律,首先需要对驱动信号进行实时处理。
2.1 超声电机驱动信号的时频处理
在超声电机启动过程中,驱动信号波形随时间的变化较为复杂,因此需要通过时频分析技术对驱动信号进行处理。经验模态分解(empirical mode decomposition,简称EMD)、小波分析和短时傅里叶变换(short-time Fourier transform,简称STFT)是常见的时频分析技术,其中EMD在处理信号时计算量较大且会引入边缘效应,导致信号的端部分析误差较大;小波分析的抗干扰能力较差,且同样受边缘效应的影响。因此,笔者选择适用于分析缓慢时变信号的短时傅里叶变换法对超声电机的驱动信号进行处理。在STFT分析中,先将信号分为不同的段,再对各段信号进行傅里叶变换来分析其特征参数,其中每一段信号称为“一帧”信号。由于超声电机驱动电压电流信号是短时平稳的,则每一帧信号的短时频谱就是各个平稳信号频谱的近似。STFT定义为
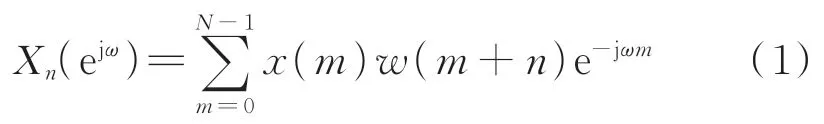
其中:x(m)为信号序列;w(m+n)为实数窗序列。
n取不同值时,窗w(m+n)将延时间轴滑动,对不同帧信号进行频谱分析。
2.2 超声电机驱动信号的频谱分析
采集的超声电机驱动信号如图3所示。由图3(c)可以看出,电压电流信号并非标准正弦信号,除了基频分量和噪声信号外,其中还包含了其他频率分量[13]使得正弦信号产生畸变。
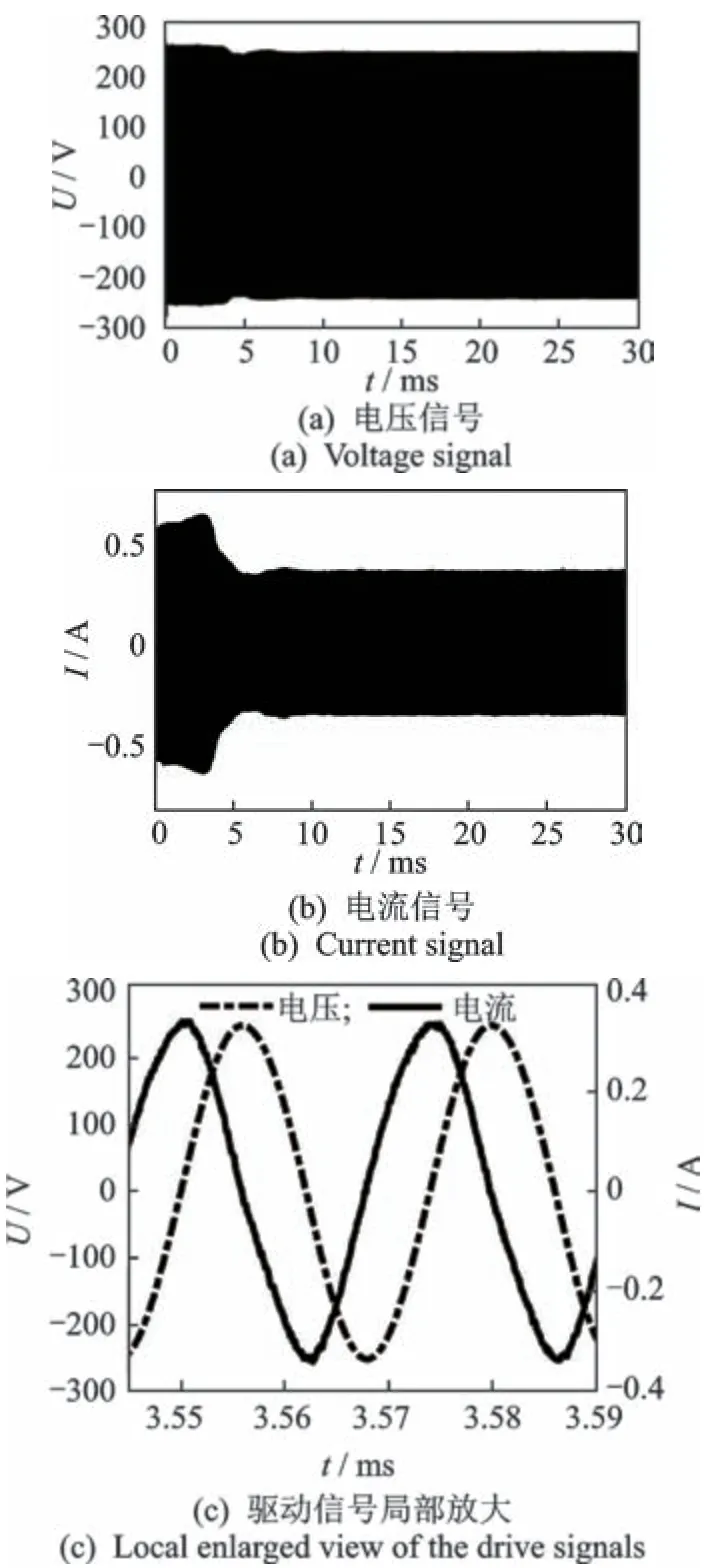
图3 超声电机驱动信号Fig.3 The drive signal of ultrasonic motor
对超声电机的驱动信号作频谱分析,如图4所示。由图可见,信号中除了直流和基频分量外,还存在以2次和3次谐波为主的高次谐波分量。
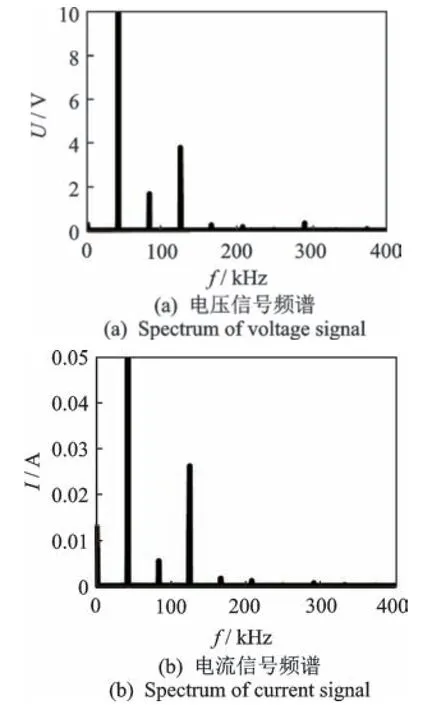
图4 超声电机驱动信号频谱Fig.4 Spectrum of ultrasonic motor driving signal
在信号的频谱分析过程中可能遇到混叠、栅栏和泄漏现象。实验中采样率为10 MS/s,超声电机工作频带为30~50 kHz,采样率远大于超声电机驱动信号频率,满足奈奎斯特采样定理,故不会出现混叠现象,因此只需要考虑泄漏和栅栏现象带来的影响。
2.2.1 基于信号加窗方法抑制频谱泄漏
由于每帧信号为有限长度,相当于给信号加上了矩形窗,将信号截断,而且实际中很难对信号整周期截取,因此出现不可避免的频谱泄漏的现象,这将会对信号各频率分量的提取和计算带来很大的误差。为减小泄漏带来的影响,应当使用性能好的窗函数。理论上要求窗函数的主瓣带宽小、频率分辨率高;同时还要使得窗函数旁瓣衰减大、旁瓣衰减速度快,这样信号在频谱分析时各频率分量之间的泄漏影响才会小。但这两个条件是相互矛盾的,不能同时满足。考虑到电参量计算的准确性,有必要牺牲频率分辨率而选旁瓣衰减大、旁瓣峰值衰减快的窗函数。笔者选用RV(Ⅲ)窗函数,其参数与矩形窗对比如表1所示。
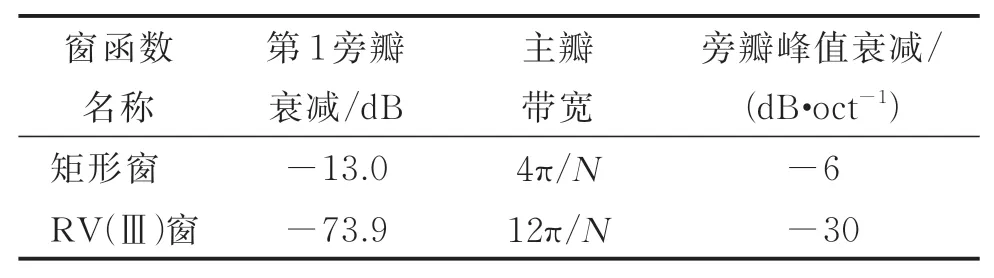
表1 矩形窗和RV(Ⅲ)窗性能对比Tab.1 Performance comparison between rectangular and RV(Ⅲ)window
从表1中可见,RV(Ⅲ)窗函数旁瓣衰减速率是矩形窗的5倍,第1旁瓣衰减远大于矩形窗,所以RV(Ⅲ)窗对频谱泄漏的抑制要优于矩形窗。但是其主瓣带宽为矩形窗的3倍,频率分辨率不足,需要较大的窗长才能弥补。如果窗长过大,相应地导致时间分辨率下降,失去瞬态测试的意义,所以需要折中选择窗函数的长度。窗长的选择计算公式为
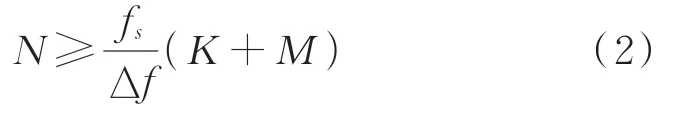
其中:fs为采样率;Δf为频率分辨率;K为选用窗函数与矩形窗的主瓣带宽之比;M为选用窗函数的旁瓣位置;N为窗函数长度。
2.2.2 基于单峰谱线插值法改善栅栏现象
在信号频谱中,信号频率f0=k0Δf,k0一般不是整数,由于栅栏现象该频率的谱线不会出现在所得频谱中。因此,笔者使用单峰谱线插值的方法,对所求频率分量进行插值修正,原理如下。
设fs为采样频率,则采样间隔为Ts=1/fs,对单一频率信号x(t)进行采样得
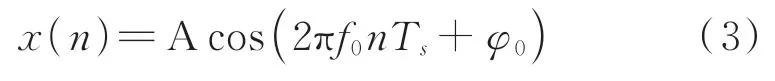
利用窗函数w(n)截断信号,可得加窗信号的离散傅里叶变换正频谱为
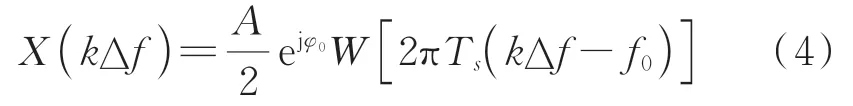
其中:W(·)为窗函数的傅里叶变换。
在信号频谱中设某频率点左右两侧的谱线序号为k1和k2,它们对应的幅值为y1=|X(k1Δf)|,y2=|X(k2Δf)|。设α=k0-k1,则α取值范围为[0,1],两谱线的幅值比为
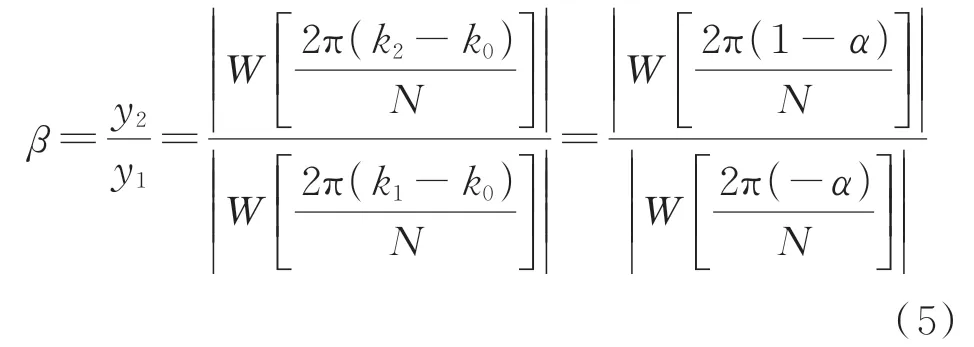
对于给定的窗函数,通过式(5)可以得到β的值以及α和β的关系,以此可以计算出频率修正量α,因此信号的频率f、相角φ0和幅值A的修正值可以由式(6)~(8)计算得到
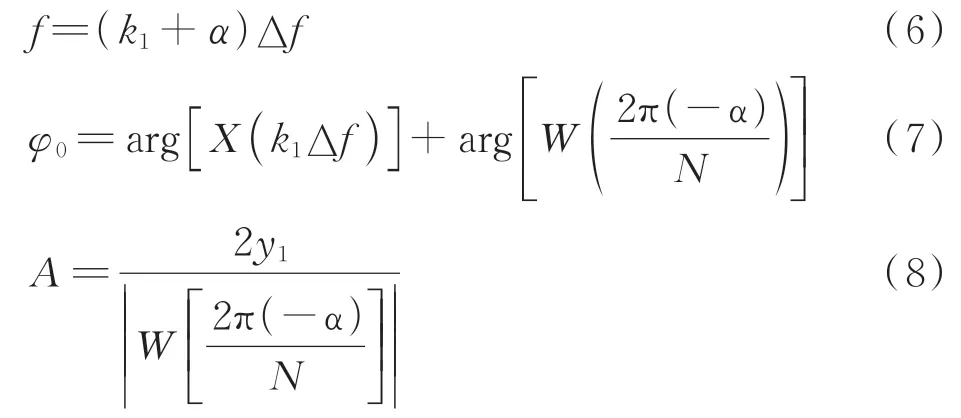
其中:arg(·)表示求复数的相角。
综上,利用加窗短时傅里叶变换的时频分析方法以及单峰谱线插值的频谱分析方法,理论上能够提取包含多频率分量信号的各频率分量的幅值、频率和初始相位,这为超声电机电参量的计算提供了基础信息。
2.3 电参量计算
对于包含高次谐波的非正弦周期信号,需要对其进行分解。由于超声电机的驱动电路分为A,B两相且对称,这里仅以A相电路进行说明。对于非正弦周期电压电流信号,可以表示为
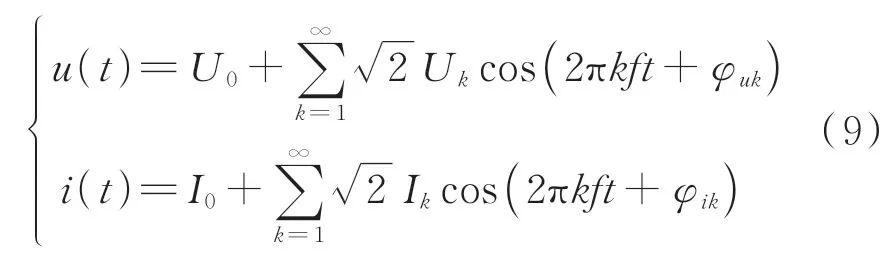
其中:U0,I0分别为电压和电流的直流分量;Uk,Ik分别为电压和电流的交流分量有效值;f为驱动信号基频;φuk,φik分别为电压和电流交流分量的初始相位。
根据上述的时频分析方法,可以得到较为精确的信号各频率分量的信号幅值、相位和频率信息。利用这些信息,可以对超声电机的电参量进行相关的计算。
利用式(9)及三角关系,超声电机的平均功率(有效功率)为
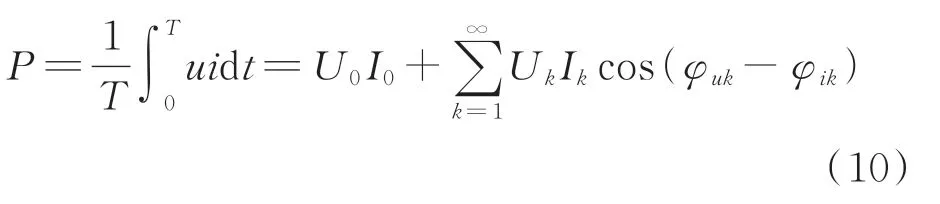
超声电机输入功率(视在功率)等于驱动电压与电流有效值的乘积
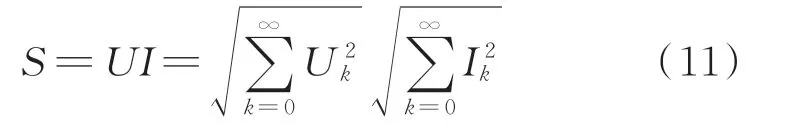
其中:U和I为电压和电流的有效值。
阻抗角(功率因数角)可表示为

阻抗角为负值表示超声电机驱动电压在时间上滞后于电流,系统呈容性;阻抗角为正值表示超声电机驱动电压在时间上超前于电流,系统呈感性。
超声电机的阻抗值、等效电阻值和等效电抗值为
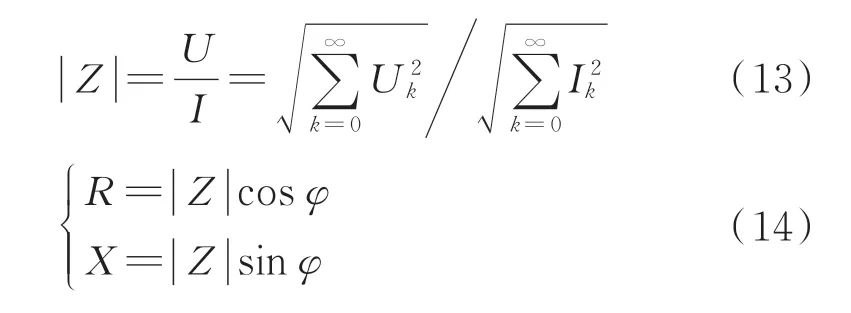
3 电参量测试方法可靠性分析
为了验证笔者提出测试方法在提取信号幅值、频率和相位差方面的可靠性与准确性,设置了1组包含基频、2次谐波和3次谐波的连续变化的仿真电压和电流信号并对其进行分析。仿真信号的公式为
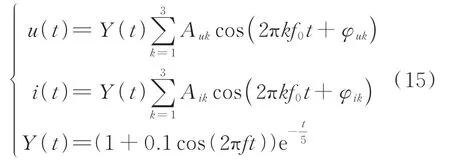
其中:f=10 Hz;f0为信号的基频;Au,Ai分别为信号的电压、电流的幅值;φu,φi分别为信号的电压、电流的初始相位。
所设置的电压电流仿真信号的采样率为10 MS/s,时长为0.1 s,信号各频率成分如表2和表3所示。

表2 仿真电压信号成分Tab.2 Components of simulated voltage signal
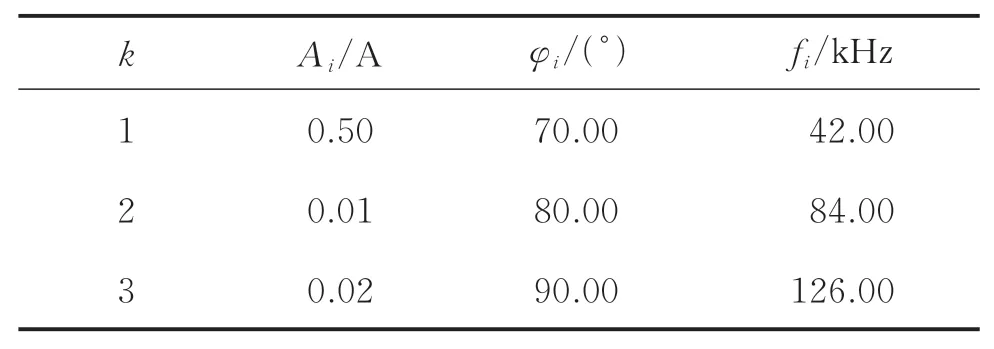
表3 仿真电流信号成分Tab.3 Components of simulated current signal
对仿真信号进行时频分析后所得各频率分量信号的幅值、频率和信号相位差的最大绝对误差如表4所示。

表4 仿真信号各频率成分的幅值、频率和相位差的绝对误差Tab.4 Error of amplitude,frequency and phase difference of each frequency component of simulation signal
由表4可见,所得信号幅值的绝对误差小于0.1 V,电压电流信号相位差的绝对误差小于0.2°,基频的绝对误差小于3 Hz,上述参数的绝对误差均小于0.5%。因此,本研究方法的计算精度可以满足电参量的计算要求。
4 实验结果及分析
利用搭建的超声电机瞬态测试系统对PMR-60/E型超声电机进行测试,测试平台如图5所示。实验中使用的驱动频率为41.8 kHz,驱动电压为500 VPP,驱动信号相位差为90°。
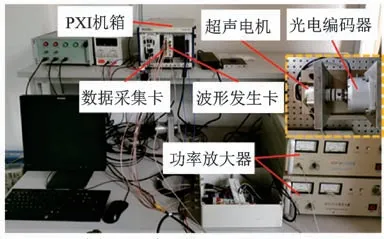
图5 瞬态测试平台Fig.5 Transient test platform
由于超声电机的驱动电路分为相互对称的A,B两相,因此瞬态电参量测试结果仅以A相的测试结果展示,测试结果如图6所示。
图6(a)为超声电机阻抗值和阻抗角,图6(b)为等效电阻和等效电抗,图6(c)为超声电机的转速、有效功率和孤极反馈电压,通过测试可以全面显示出超声电机瞬态下状态参数的变化过程。从测试结果中可以清楚地看出,超声电机从启动到稳定运行的过程中存在两个变化过程,在时间上划分为(0,t0)和(t0,t1)两个阶段,称之为超瞬态阶段和次瞬态阶段[16]。
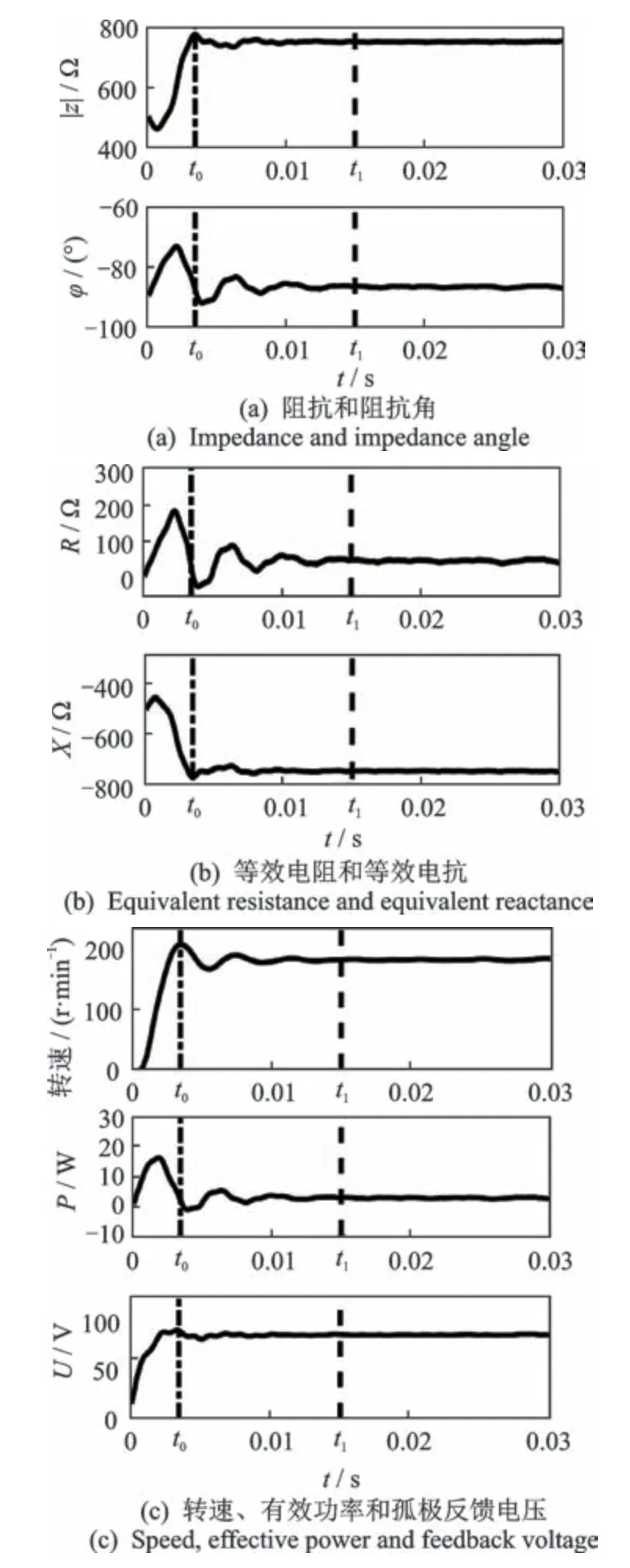
图6 超声电机电参量测试结果Fig.6 Test results of electrical parameters of ultrasonic motor
在超瞬态阶段,电机处于加速状态,电机的孤极反馈电压幅值不断增大,电机定子的振幅也随之增大,压电振子的正压电效应也随之增强,产生的电流反馈给驱动电流导致通过电机的电流减小而使得电机的电参量变化剧烈。阻抗随时间增加从450Ω逐渐增加到780Ω,最大值约为最小值的1.7倍;等效电抗与阻抗的绝对值的变化规律一致,等效电阻的变化规律与阻抗角一致;阻抗角先减小后增大导致电机有效功率先增大后减小,阻抗角的最大值与最小值之间的差值约有17°。
在次瞬态阶段,由于电机定转子之间储存了一定的弹性势能,此时弹性势能与机械能之间的相互转化使得电机的压电振子的振动状态发生改变,在阻尼的作用下孤极反馈电压处于衰减振荡状态,电机转速也在衰减振荡;相应的电机阻抗、阻抗角等相关电参量均处于衰减振荡的状态,阻抗最大衰减量达到50Ω,阻抗角最大变化量达到10°左右。在时间t1之后各项参数趋于稳定,超声电机基本处于稳定运行状态。
5 结论
1)提出了一种用于超声电机启动瞬态下的电参量测试方法,该方法可以较为全面地测试超声电机启动瞬态下的阻抗、阻抗角等相关电参量的变化曲线,且具有良好的测试精度,可用于分析超声电机启动瞬态的响应特性。
2)搭建了超声电机瞬态测试系统并对PMR-60/E型超声电机进行了测试,结果表明:在电机启动的超瞬态和次瞬态两个阶段中电参量变化剧烈,阻抗值的相对变化最大约为70%,阻抗角相对变化最大约为17%。
