关于图Pa,b的邻点可区别染色
2022-11-04严谦泰
严谦泰
(安阳师范学院 数学与统计学院,河南 安阳 455000)
1 研究背景
图的染色是图论的重要研究内容,由计算机科学和信息科学等所产生的一般点可区别边染色[1]、邻点可区别边染色[2-6]、邻点可区别全染色[7]、邻点强可区别全染色[8]等染色法,这些都是十分困难的问题,至今文献甚少。文中将通过具体的染色方法,给出图Pa,b的邻点可区别边染色数、邻点可区别全染色数、邻点强可区别全染色数。

定义2[7]图G(V,E)的一个正常全染色f:V∪E→{1,2,…,k},如果满足:
1)对任意的uv∈E有f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv);
2)对任意的uv,vw∈E有f(uv)≠f(vw),且C(u)≠C(v)。
则称f是图G(V,E)的一个邻点可区别全染色,简记为k-AVETC。在k-AVDTC中最小的数k称为图G(V,E)的一个邻点可区别全染色数,记为χat(G)=min{k|k-AVDTC}。
定义3[8]设G(V,E)是阶数不小于3的简单连通图,f是从V(G)∪E(G)到{1,2,…,k}的映射,满足:
1) 对任意的边uv∈E(G),f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv);
2)对任意的两相邻边uv,uw∈E(G)(v≠w),f(uv)≠f(uw);
3)对任意的边uv∈E(G),其端点的色集合满足C(u)≠C(v),其中一顶点u的色集合
C(u)={f(u)}∪{f(v)|uv∈E(G)}
∪{f(uv)|uv∈E(G)}
则称f是图G的一个邻点强可区别的全染色,简记作k-AVSDTC,且称数
χast(G)={k|G所有的k-AVSDTC}
为G的邻点强可区别的全染色数。
定义4[9]设u,v是两个固定顶点,用b条内部互不相交且长度均为a的道路连接u,v的图用Pa,b表示。
本文涉及的图都是简单连通有限图,未加说明的术语与记号见文献[10]。
2 主要结论及其证明

引理2[7]如果简单图G是阶不小于3的图,则χat(G)≥Δ(G)+1;如果简单图G有两个相邻的最大度顶点,则χat(G)≥Δ(G)+2。
引理3[8]如果简单图G是阶不小于3的图,则χast(G)≥Δ(G)+1;而G中至少有最大度顶点相邻,则有χast(G)≥Δ(G)+2。
引理4[8]对于n阶路Pn(n≥3),有
χast(Pn)={4,n≡0(mod 2)
5,n≡1(mod 2)
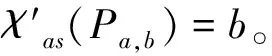

……
即第1条路上的边用1,2,…,b循环染色;第2条路上的边用2,3,…,b,1循环染色;第3条路上的边用3,4,…,b,1,2循环染色;……;第b条路上的边用b,1,2,…,b-1循环染色。这是Pa,b的一个b-AVDEC。
定理2 对于图Pa,b(a≥3,b≥3),有χat(Pa,b)=b+1。
证明 情形1 对于图Pa,3(a≥3),有χat(Pa,3)=4。
由于Δ(Pa,3)=3,由引理2知,χat(Pa,b)≥4,下证χat(Pa,b)=4。Pa,3中每条路上一共有2a+1个顶点和边。


故f是Pa,3的4-AVDTC。





故f是Pa,3的4-AVDTC。
综上可知,χat(Pa,3)=4。
情形2 对于图Pa,b(a≥3,b≥4),由于Δ(Pa,b)=b,故χat(Pa,b)≥b+1,下证χat(Pa,b)=b+1。Pa,b(a≥3,b≥3)中每条路上一共有2a+1个顶点和边。

第1条路上前2a个顶点和边用1,2,…,b,b+1循环染色;
第2条路上的顶点和边用1,3,4,…,b+1,2循环染色;
第3条路上的顶点和边用1,4,5,…,b+1,2,3循环染色;
……
第b条路上的顶点和边用1,b+1,2,3,…,b循环染色。
这是Pa,b的一个(b+1)-AVDTC。




……

这是Pa,b的一个(b+1)-AVDTC。




……

这是Pa,b的一个(b+1)-AVDTC。
一般地,当2a+1≡i(mod(b+1))时,



……
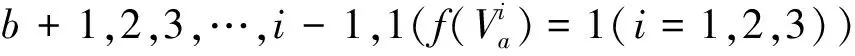




……

综上可知,f是Pa,b的一个(b+1)-AVDTC。
定理3 对于图Pa,3(a≥4),有
χast(Pa,3)={4,a≡0(mod 2)
5,a≡1(mod 2)

情形1.1 当a≡0(mod 3)时,此时2a是3的倍数。

当i≡1(mod 2)时:
当i≡1(mod 2)时:
当i≡1(mod 2)时:
这是Pa,3(a≥4)的一个4-AVSDTC。
情形1.2 当a≡1(mod 3)时。

当i≡1(mod 2)时:
当i≡1(mod 2)时:
当i≡1(mod 2)时:
这是Pa,3(a≥4)的一个4-AVSDTC。
情形1.3 当a≡2(mod 3)时。

当i≡1(mod 2)时:
当i≡1(mod 2)时:
当i≡1(mod 2)时:
这是Pa,3(a≥4)的一个4-AVSDTC。

情形2.1 当a≡0(mod 5)时,
这是Pa,3(a≥4)的一个5-AVSDTC。
情形2.2 当a≡1(mod 5)时,
这是Pa,3(a≥4)的一个5-AVSDTC。
情形2.3 当a≡2(mod 5)时,
这是Pa,3(a≥4)的一个5-AVSDTC。
情形2.4 当a≡3(mod 5)时,
这是Pa,3(a≥4)的一个5-AVSDTC。
情形2.5 当a≡4(mod 5)时,
这是Pa,3(a≥4)的一个5-AVSDTC。
综上可知,χast(Pa,3)={4,a≡0(mod 2)
5,a≡1(mod 2)。
定理4 对于图Pa,b(a≥4,b≥4),有χast(Pa,b)=b+1。

情形1 当a≡0(mod 5)时。
第i条路上的顶点用1(i+1)(i+2)(i+3)(i+4)循环染色,i=1,2,…,b,其中i+1,i+2,i+3,i+4(≥b+2)是在模b(modb)的意义下。 第i条路上的边用(i+2)(i+3)(i+4)1(i+1)循环染色。同定理3可验证f是Pa,b(a≥4,b≥4)的一个(b+1)-AVSDTC。
情形2 当a≡1(mod 5)时。

情形3 当a≡2(mod 5)时。
第i条路上的顶点用1(i+1)(i+2)(i+3)(i+4)循环染色,i=1,2,…,b,其中i+1,i+2,i+3,i+4(≥b+2)是在b(modb)模的意义下。 第i条路上的边用(i+2)(i+3)(i+4)1(i+1)循环染色。可验证f是Pa,b(a≥4,b≥4)的一个(b+1)-AVSDTC。。
情形4 当a≡3(mod 5)时。

情形5 当a≡4(mod 5)时。
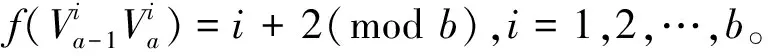
综上可知,对图Pa,b(a≥4,b≥4),有χast(Pa,b)=b+1。
