基于旋转天线的二维高分辨成像算法
2022-11-03王志浩
王志浩,张 群,袁 航
(空军工程大学信息与导航学院,西安,710077)
电磁涡旋成像是近年来比较热门的新体制雷达成像技术。雷达发射携带轨道角动量(orbital angular momentum, OAM)的涡旋电磁波照射目标区域,利用涡旋电磁波的螺旋形相位波前分布和不同轨道角动量本征态之间的正交性,可以在雷达与目标不发生相对运动的情况下对目标区域进行凝视成像[1-2]。研究表明,轨道角动量的模式数与目标方位角之间具有近似对偶关系,同时涡旋电磁波的带宽与目标距离之间也存在对偶关系,因此利用携带轨道角动量的涡旋电磁波可以实现对目标的二维成像[3]。文献[4]针对噪声的影响提出了一种基于分数阶轨道角动量的电磁涡旋增强成像方法,能够提升低OAM阶数和复杂噪声场景下的成像性能。
电磁涡旋成像的方位角分辨率对轨道角动量模式数具有较高的要求,然而在现有的技术条件下,难以获得纯净的多模态涡旋电磁波,极大地制约了方位角的高分辨能力[5]。已有的涡旋电磁波产生方式主要有涡旋相位平板(spiral phase plate, SPP)、微波天线、超材料表面和均匀圆形阵列(uniform circular array, UCA)[6]等方法。相较于前3种方式,均匀圆形阵列可以灵活地控制每个阵元相位,通过控制各阵元初始激励相位或阵元信号通断时间,实现相位的特定改变,产生携带不同模式数的涡旋电磁波,更适用于雷达探测、成像等领域[6]。然而,纯态涡旋电磁波要求携带整数阶OAM模态的涡旋电磁波的相位随方位角严格地线性变化,而在推导涡旋电磁波的电场分布时采用了积分代替求和的近似,这说明只有无限密的空间采样才会产生理想纯态的涡旋电磁波,因此,实际中有限阵列调相的方式不可能产生理想纯态的涡旋电磁波,从而制约了涡旋电磁波雷达的成像能力[7]。
根据相对运动形式可以将成像方法分为3类,分别是雷达静止且目标静止的凝视成像方法[8]、雷达静止且目标运动的逆合成孔径成像方法[9-10]和雷达运动且目标静止的合成孔径成像方法[11]。基于圆环天线阵列的涡旋电磁波雷达成像方法属于第一类,文献[10]针对自旋运动目标成像问题,利用目标自旋运动产生的方位角建立成像模型,获得方位角分辨率,然后利用不同时延的正交编码信号,在短时间内获得足够多的等效脉冲,最后利用修正SL0算法,实现了对自旋运动目标的短时观测成像,此方法属于上述方法中的第二类。文献[11]提出将雷达绕圆周运动会将目标投影到不同的方向,因此可以得到被检测目标的Radon变换,再通过逆Radon变换即可重建出目标的三维像,但此方法针对的是近场静止目标的成像问题。针对以上问题,本文从基于圆环天线阵列的涡旋电磁波产生方法和自旋运动目标成像方法中获得启发,提出了一种基于旋转天线的二维高分辨成像方法,利用天线旋转产生的正线多普勒曲线,重构出目标的方位角信息,在雷达波束范围内实现对静止目标的二维高分辨成像。
1 雷达观测模型
如图1所示,假设自由空间中存在一散射点P,其在球坐标系下可被表示为P(rP,θP,φP),其中rP为散射点到坐标原点距离,θP为散射点俯仰角,θP∈(0,π/2),φP为散射点方位角,φP∈(-π,π)。在空间直角坐标系下表示为P(xP,yP,zP),P在XOY平面上的投影点为M。阵元以点(a,0,0)为初始点,以原点O为圆心,做半径为a的逆时针圆周运动,圆周运动频率为f。收发阵元位置随慢时间tm的变化过程Q(tm)可表示为:
Q(tm)=(acos(2πftm),asin(2πftm),0)
(1)
则阵元与散射点的距离rP(tm)可被表示为:
rP(tm)=‖(xP,yP,zP)-Q(tm)‖
(2)
式中:‖·‖表示求向量的模。运用Fresnel近似方法,可将式(2)近似表示为:
rP-asin(θP)cos(2πftm-φP)
(3)
阵元发射线性调频信号:
(4)
式中:t为快时间; rect(·)为矩形窗函数;TP为脉冲持续时间;fc为载频;γ为调频率;j为虚数单位。
在一个脉冲持续时间内,散射点与雷达之间可近似视为相对静止,则接收回波secho(tm,t)可被表示为:
exp(j2π(fc(t-τP(tm))+0.5γ(t-τP(tm))2))
(5)
式中:σP为散射系数;回波时延τP(tm)=2rP(tm)/c,c为光速。当存在n个散射点时,回波secho(tm,t)可被重写为:
exp(j2π(fc(t-τP(tm))+0.5γ(t-τP(tm))2))
(6)

图1 雷达与目标的几何关系
2 成像算法
设参考信号sref(t)为:
sref(t)=exp(-j2π(fct+0.5γt2))
(7)
对式(6)作“Dechirp”处理,得到:
Secho(tm,fr)=FFT{secho(tm,t)·sref(t)}·
exp(-j2πfcτP(tm))
(8)

(9)
设单个距离单元内存在L个散射点,单个距离单元的信号Sunit(tm)可被表示为:
(10)

(11)
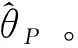
(12)
式中:arcsin(·)为反正弦函数。
D=[d1,d2,…,dm]
(13)
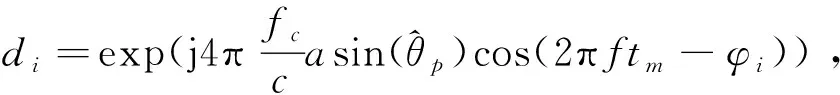
i=(1,2,…,k),k表示将方位角在(-π,π)范围内等分的个数。
OMP算法的优化目标可被表示为:
(14)

Step1 初始化:残差r0=y,索引位置Λ0=∅,D0=∅,迭代次数计数器t=1;
Step2 求解:λt=argmaxi=1,2,…,k|
Step3 扩充:Λt=Λt-1∪(λt),Dt=[Dt-1,dλt];
Step4 求解最优化问题:

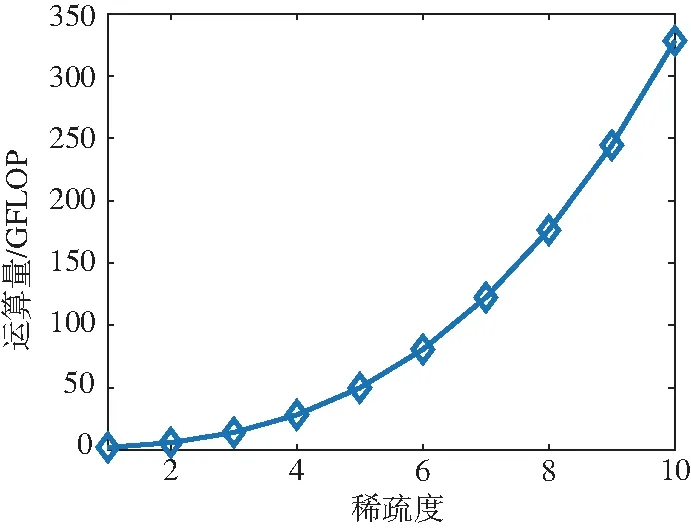
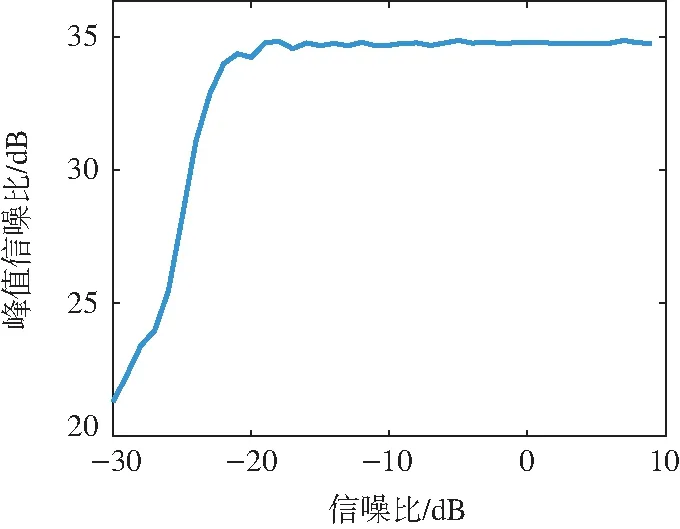
Step6t:=t+1,若t Step7 最终的索引位置Λ即方位角对应的位置。 整个成像算法的过程如图2所示。 图2 成像算法流程图 本成像方法的距离分辨率ar由线性调频信号的带宽B决定: (15) 点散布函数(point spread function, PSF)可以表征成像雷达的分辨率,也被称为成像雷达系统的点目标脉冲响应函数。根据文献[13],基于旋转天线的目标方位角PSF可以被描述为: (16) 式中:A表示常数,Δ表示方位角的变化量;k=2πfc/c;R表示目标点与雷达之间的距离;R′表示目标方位角变化Δ后目标与雷达之间的距离;φ表示雷达探测的方位角范围。 在本文的雷达观测模型中: R=rP-asin(θP)cos(2πftm-φP) (17) R′=rP-asin(θP)cos(2πftm-φP+Δ) (18) 将式(17)和(18)代入式(16)可以得到: (19) 当方位角为0 rad时,PSF可以写成 (20) (21) 式中:发射信号波长λ=c/fc。 上述结果计算场景为方位角为0 rad,不同方位角下PSF的特性将在仿真实验中进一步研究。 雷达系统参数设置见表1,仿真实验中设置了17个散射点,具体位置见图3。 表1 雷达仿真参数设置 图3 理想成像结果 首先对回波信号作“Dechirp”处理,可以获得17个散射点的一维距离像,距离向成像结果见图4可以看出,17个散射点目标一共有9个距离单元,一维距离像的尖峰比较突出,可以被准确地重建出来。 图4 距离向成像结果 410 m处距离单元存在2个初相不同的散射点,提取信号,得到其时频图,结果见图5。 图5 距离单元为410 m时的信号时频图 本成像方法的方位角成像结果见图6。11个散射点目标共有9个方位角单元,重构出的方位角与理想结果的偏差极小,不影响对目标成二维像。 图6 方位角向成像结果 在回波信号中加入复高斯白噪声,信噪比为0 dB,目标的距离和方位角被准确重建,二维成像结果见图7。 图7 信噪比为0 dB时的成像结果 本文采用仿真的方式,得到不同方位角下PSF图像。选取方位角分别为0 rad和1 rad时的PSF图像进行分析,见图8,从图中可以看出不同方位角下的PSF基本一致,不同的方位角对分辨率的影响极小,因此本算法用方位角为0 rad时的分辨率。在给定的仿真参数下,方位角分辨率为0.06 rad。 图8 方位角分别为0 rad、1 rad时的PSF 公式(3)是由Fresnel近似得到的,目标距离、俯仰角和方位角均会影响近似结果。定义雷达与目标之间的距离和近似距离的偏差为近似误差。图9分别给出了近似误差分别随目标距离、方位角和俯仰角的变化过程。分析图9可得,近似误差随着目标距离的增大而减小。在给定的仿真条件下,雷达发射信号的波长为0.03 m,在目标距离小于50 m时,误差急剧增大,近似误差与信号波长相比无法忽略,因此在目标距离小于50 m时近似误差会对相位产生较大影响,成像质量较低;当目标距离大于50 m时,近似误差急剧下降,仅不足0.5 mm,对相位产生的影响可以忽略不计,成像质量较为稳定,可以对远场目标进行高分辨成像。方位角和俯仰角的变化对近似误差的影响极小,因此对成像质量的影响不显著。 图9 近似误差随目标距离、方位角和俯仰角的变化过程图 目标距离对近似误差的影响比方位角和俯仰角对近似误差的影响高一个数量级,因此方位角和俯仰角对近似误差的影响可以忽略不计。 为客观分析各参数对成像质量的影响,本文引入峰值信噪比(peak signal-noise ratio, PSNR)作为评价成像质量的标准,PSNR越大,成像质量越好[14]。 成像质量随目标距离的变化过程如图10所示,随着距离的增大,图像的PSNR增大,成像质量提高,当目标距离增加到50 m后,PSNR趋于稳定,目标距离不再显著影响成像质量,由此也可以看出该算法可以对远场目标进行高分辨成像。 图10 成像质量随目标距离的变化过程 为了展示本文成像方法的优势,现将本文所提方法与距离多普勒(range Dppler, RD)算法、线性调频变标(cirp saling, CS)算法、频率变标(fequency saling, FS)算法、omega-K算法和后向投影(back projection, BP)算法的成像结果相比较,对比结果如图11所示。从图中可以看出本文方法所成的二维像旁瓣最低,展示了很好的成像性能。 图11 本文方法与其他方法的对比 本文所提方法涉及的操作有:距离向快速傅里叶变换、复数相位相乘和正交匹配追踪算法。假设估算浮点运算量(FLOP)的参数分别为[15]:输入距离线数Naz=4 096,每一输入距离线上的采样点数Nrg=4 096,插值核长度Mker=8。距离向快速傅里叶变换操作的GFLOP为5NazNrglog2(Nrg)/109=1.01;复数相位相乘的GFLOP为6NazNrg/109=0.1;正交匹配追踪算法的GFLOP为[24]: 式中:M表示距离单元的个数,K表示信号的稀疏度。本文所提算法的浮点运算量GFLOP如图12所示,当稀疏度K=1时,浮点运算量为2.217 GFLOP,当稀疏度K=2时,浮点运算量为6.043 GFLOP,运算量相对较小。 图12 运算量随稀疏度的变化过程 在数据大小相同的条件下,RD算法的浮点运算量为4.08 GFLOP,CS算法的浮点运算量为4.05 GFLOP,含Stolt插值的omega-K算法的浮点运算量为4.38 GFLOP, FS算法的浮点运算量为4.58 GFLOP[16]。在稀疏度较低的情况下,以上4种算法的浮点运算量均与本文算法在同一数量级。假设成像区域像素点为2 048×2 048,则BP算法的浮点运算量为138.85 GFLOP,远高于其他成像算法,这是因为BP算法采用的是逐点反投影成像的方法。各成像算法的运算量和运行时间如表2所示。 综合来看,本文所提方法的成像效果最好,同时在稀疏度较低的情况下运算量与RDA、CSA、FSA和 omega-K算法在同一数量级,优于BP算法。 表2 各成像方法的浮点运算量和运行时间 假设涡旋电磁波的模态数范围为Δα,则在多发多收(multiple input multiple output, MIMO)模式下的电磁涡旋成像方位角分辨率az=π/Δα。如果要达到0.06 rad的方位角分辨率,则需要的模态数范围Δα=53。当前技术条件下能够产生的纯净涡旋电磁波模态数范围远远达不到53,因此本文提出的高分辨成像方法具有较好的应用优势。 下面分析成像质量随信噪比的变化过程。如图13所示,随着信噪比的增大,PSNR逐渐增大,在信噪比大于-19 dB后趋于稳定。 图13 信噪比对成像质量的影响 当信噪比为-19 dB时,成像质量趋于稳定。本成像方法能够在如此低的信噪比下成像的原因是:复高斯白噪声是不相关的,而雷达发射的信号具有相关性,当对接收的回波信号进行傅里叶变换时,只有与目标位置信息相关的信号得到增强,抗噪能力大大提升。本成像方法的鲁棒性得到了验证。 本文建立了旋转天线观测模型,提出了基于旋转天线的二维高分辨成像算法。雷达发射线性调频信号,可对空中的静止目标进行高分辨成像,同时结合正交匹配追踪算法,使得散射点旁瓣被有效抑制。通过与电磁涡旋成像方法对比发现,如果电磁涡旋成像方法要达到和本成像方法的相同的方位角分辨率,需要较高的模态数范围,这在现有的技术条件下难以达到。与传统SAR成像方法相比,在运算量相近的情况下,本文方法的成像旁瓣更低,成像质量更好。本模型只需要一副天线即可完成信号发射和回波数据采集,对雷达性能的要求不高,大大降低了成像的成本。未来将进一步验证本方法在实际场景中的性能。
3 成像分辨率分析
3.1 距离分辨率分析
3.2 方位角分辨率分析



4 仿真验证
4.1 算法有效性仿真分析

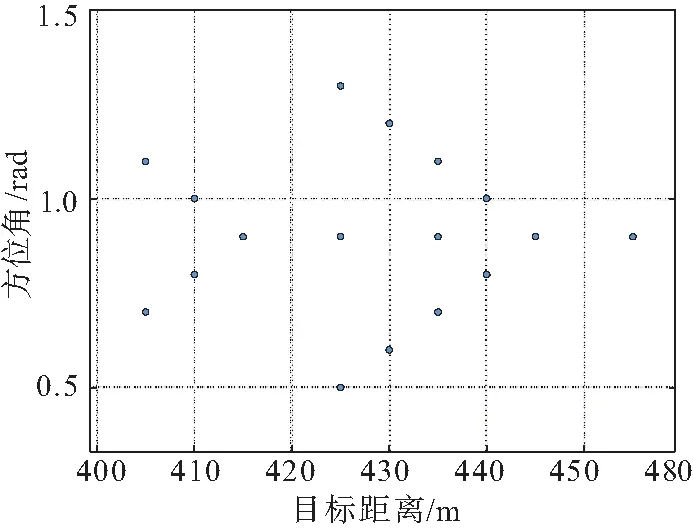




4.2 算法分辨率仿真分析
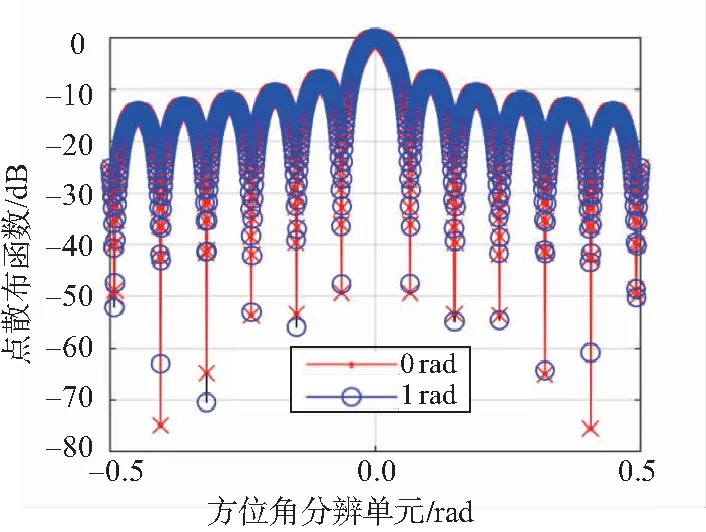
4.3 各参数对成像质量的影响


4.4 与其他成像算法的对比


4.5 算法鲁棒性仿真分析
5 结语
