多轮多支柱起落架地面转弯载荷分析与预测

谢 帅，杨全伟

(中国飞行试验研究院，西安， 710089)

飞机的大角度转弯能力可以减少占用跑道时间，降低跑道宽度要求，有效提高飞机的机动能力和运营能力。转弯速度越大，转弯半径越小，飞机的大角度转弯能力越好，但发生侧滑、翻倒和载荷超限的风险越高。前三点式小型飞机仅有一排主起落架，转弯时前起落架和主起落架侧向载荷均指向转弯内侧方向，侧向载荷和垂向载荷可以根据地面运动方程进行计算；对于主起落架具有前、中、后3个支柱的多轮多支柱大型飞机，其起落架结构本身超静定，传力路径复杂，缓冲器的功量分配不同，转弯时各支柱和各轮胎动态协调分配载荷，主起落架单个支柱的侧向载荷和垂向载荷分配难以通过理论计算确定，仿真结果的正确性和可靠性也难以保证[1-4]。

欧美俄有A400M、A380、C-5A、波音747、伊尔76、安225等多轮多支柱起落架布局成熟的大型军民用运输机，但在起落架载荷测量方面公开发表的资料很少，工程上经常参考的是使用应变法测量起落架载荷的经典著作[5-6]。在飞行试验方面，国内使用应变法对多型前三点式国产飞机及引进的伊尔76五支柱式飞机的起落架载荷进行了飞行实测[3,7-8]，对前三点式和五支柱式飞机的起落载荷规律有较为成熟的认识；在理论研究方面，国内开展了大量的飞机起落架地面转弯计算与仿真研究[4,9-23]，包括基于刚性轮胎理论的双轮式、四轮小车式和六轮小车式起落架稳定转弯侧向载荷计算[9]，基于弹性轮胎理论的多轮多支柱起落架的低速地面转弯能力计算[4]，以及基于ADMAS的多轮多支柱起落架和小车式起落架地面转弯载荷仿真分析[10-11]等，理论计算均基于前三点式飞机的瞬心法，将主起落架视为一个整体进行考虑，商用软件虽然可以得到各个轮胎的载荷，但是模型未使用试验数据修正，难以对飞行试验提供可靠支持。

某型飞机的前起落架为双轮单支柱式，每侧主起落架为串列三支柱式，单个支柱均有两个机轮，属于典型的多轮多支柱布局。地面极限转弯试验需要操纵飞机以最小转弯半径和最大转弯速度进行稳定转弯，试验风险较高，因此本文开展多轮多支柱飞机地面转弯起落架载荷分析与预测研究。

1 地面转弯分析

1.1 地面转弯运动分析

考虑轮胎弹性时，只要轮胎的中心线与运动方向成一个角度，则轮胎的胎面与跑道路面接触时，在某种程度上就一定会移动。大多数移动发生在接地中心的后面，接地中心到移动面积中心的力臂称为气胎稳定距，移动引起的侧向载荷会引起绕接地中心的一个力矩。该侧向载荷称为抗侧滑力，该力矩称为抗侧滑力矩。单个机轮的侧滑示意见图1[24]。

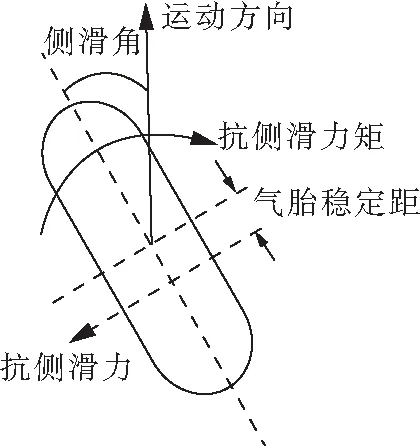
图1 单个机轮侧滑示意图

飞机设计手册给出了常规三点式和多轮小车式起落架的地面运动模型和简化分析，侧向载荷均将主起落架视为一个整体，施加于轮轴或车架中心处；垂向载荷则根据全机和小车轮架的受力平衡计算得到单个轮轴的垂向载荷[1]。对于该型多轮多支柱起落架，需要知道侧向载荷和垂向载荷在主起落架前、中、后3个支柱上分配情况，才能建立准确的起落架载荷预测模型。依据上文介绍的单轮侧滑原理，建立某型飞机多轮多支柱起落架的地面转弯运动分析图，见图2。

图2 多轮多支柱起落架地面转弯运动分析图

图2中：1～6为主起落架的编号；α为前轮操纵角；β为重心切线速度与飞机对称面的夹角；e为前起落架稳定距；O为转弯中心；O1为飞机重心；a为重心站位至前轮胎中心的距离；b为主起落几何中心距重心的航向距离；c为转弯中心至飞机对称面的距离；r为飞机惯性半径(O到O1)；v为飞机重心速度方向；vi(i=1，2，…，6)为6个主起落架的速度方向；Fny为前起落架侧向载荷；Fiy(i=1，2，…，6)为主起落架各个支柱的侧向载荷；Fin为转弯离心力；Fnx为前起落架滚动摩擦力；F0为发动机推力、飞机阻力和主起落架滚动摩擦力的合力。

本文的载荷方向定义：正航向为正，指向左侧为正，垂直地面向上为正。

本文的分析基于以下假设：①速度瞬心假设，即用运动的瞬时中心代表飞机运动轨迹的曲率中心，前轮操纵角速率为0；②瞬时转动中心与主起落架中支柱轮轴中心位于同一航向站位；③油门位置固定；④不采用差动油门；⑤不采用差动刹车。

根据上述多轮多支柱布局飞机的地面运动分析图，建立前轮操纵角、飞机惯性半径和飞机几何尺寸之间的关系，见下式：

r=b/sinβ

(1)

c=b/tanβ

(2)

(3)

联合求解式(1)～(3)，可得式(4)：

(4)

式(4)中a、b、e为飞机的几何参数，仅与重心位置有关，转弯过程中可近似认为重心位置不变，则这3个参数为固定值；当操纵飞机前轮进行地面稳定转弯时，α也视为固定值，可知此时飞机惯性半径r也为固定值。由于主起落架位置与重心的相对位置固定，因此此时主起落架各个支柱上的局部转弯半径也为固定值。

1.2 起落架侧向载荷分析

根据图2，建立外力在OO1方向(飞机离心力方向)的平衡方程，见下式：

(5)

Fin=mv2/r

(6)

结合弹性轮胎理论可知：地面转弯时，主起落架前、中、后3个支柱的瞬时速度方向和轮胎侧滑角均不相同，可知侧向载荷的方向和大小也均不相同。但起落架侧向载荷有以下规律：由于前起落架为主动转向轮，侧滑角较小，因此侧向载荷较小，且方向指向转弯中心；主起落前支柱侧向载荷指向转弯外侧方向，中支柱侧向载荷为零(基于瞬时转动中心与主起落中支柱位于同一航向站位的假设)，后支柱侧向载荷指向转弯内侧方向，式(5)右侧第1项为正时，起落架侧向载荷之和才可提供足够的转弯向心力；主起落架前后支柱的侧向载荷产生对机身的不利扭矩，与五支柱起落架类似[3]。

1.3 起落架垂向载荷分析

六轮小车式起落架仅有1个支柱，6个机轮是通过车架相连；该型多轮多支柱飞机的单侧主起落架虽然也有6个机轮，但是有3个支柱，成对机轮之间相对独立，垂向载荷分配与支柱缓冲器的填充参数有关，无法通过小车式起落架的力矩平衡[1,9]来等效计算。因此，虽然前起落架和主起落架的垂向载荷满足力及力矩平衡方程，见式(7)、(8)，但主起落架单个支柱的垂向载荷难以通过理论计算得到。

(7)

(8)

式中：bi为标号为i的主起落架支柱几何中心距重心的航向距离。

因此，仅对转弯时起落架各个支柱上的垂向载荷进行定性理论分析。转弯时在离心力的作用下，会产生翻倒力矩，内侧主起落架垂向载荷减小，前起落架和外侧主起落架垂向载荷增大。

1.4 地面稳定转弯条件分析

飞机实现稳定转弯需满足3个条件：起落架轮胎不会侧滑、飞机不会翻倒和起落架载荷不超限制。

侧滑分析：当轮胎侧向力(起落架侧向载荷)超过轮胎与地面的极限侧向摩擦力，飞机会发生侧滑。由1.2节可知，主起落架前、后支柱机轮发生侧滑的概率较高，且侧滑方向相反；中支柱机轮发生侧滑的概率较低。主起落架机轮侧滑会使飞机转弯半径减小，加之侧滑速度的叠加，从而使Fin增大，此时飞机急剧转弯，会有翻倒的风险。

翻倒分析：参考前三点式飞机的翻倒受力分析[1]，该型多轮多支柱起落架的翻倒轴可视为前起落架轮心到外侧主起落架中支柱的轮心连线。飞机翻倒时的力矩平衡方程为：

FturnH=(G-Y)S

(9)

地面作用于轮胎的合力(取反向)在翻倒轴垂线上投影为：

Ff≈F0sinβ+Fin

(10)

飞机不发生翻倒的条件为：

Ff/Fturn<1

(11)

引入飞机防翻倒储备系数,可表示为：

(12)

式中：H为飞机重心高；Fturn为翻倒力；G为飞机重力；Y为飞机升力；S为防翻倒力臂(重心到翻倒转轴之间的投影距离，翻倒轴为前轮及4号主轮接地点的连线)；K为防翻倒储备系数(参数范围0～1,值为0时飞机翻倒)。

转弯时速度较低，假设升力Y为0，F0sinβ为小量也假设为零，则式(12)可简化为：

(13)

将飞机极限转弯速度v、半径r和飞机几何参数H和S代入式(13)，得到极限转弯时飞机的防翻倒储备系数为0.62，可知飞机极限转弯时防翻倒储备系数较高，但仍需关注单个起落架的组合受载情况。

载荷超限分析：当起落架的侧向载荷超过自身设计限制，从而会导致爆胎甚至起落架结构损伤。

综合以上分析可知，该型飞机在极限转弯时发生翻倒的概率低，主起落架前、后支柱为受载最严酷的起落架支柱，因此需关注其侧向垂向载荷组合是否超限。

2 地面转弯起落架载荷预测模型

首先依据循序渐进的原则，建立了两种逐步逼近极限转弯的试验策略，并根据实测得到的起落架载荷对上文中的分析结论进行验证，然后建立两种策略下的起落架载荷预测模型，使用实测样本点对模型参数进行估计。

2.1 转弯试验

转弯试验是飞机地面载荷飞行试验的重要组成部分，主要用于验证起落架的侧向垂向载荷组合是否满足设计要求。极限转弯试验时，飞行员逐步增大前轮操纵角直至最大，调整油门使飞机速度达到该操纵角对应的最大转弯速度，保持该状态进行稳定地面转弯运动，飞机运动过程如图3所示。

图3 极限转弯试验飞机运动过程示意图

试验时，采用2种策略逐步逼近极限状态：①飞行员操纵飞机达到极限转弯速度，逐步增大前轮操纵角转弯至最大值；②飞行员操纵飞机达到最大前轮操纵角，逐步增大速度直至最大值。

起落架地面转弯载荷测量使用应变法进行，通过在起落架关键结构部位粘贴感受弯矩、扭矩和拉压的应变电桥，利用地面载荷校准试验建立外载荷和应变电桥之间的关系，最终在飞行试验中实测起落架应变值，从而计算得到起落架载荷。应变法测载原理如下：

(14)

式中：ε为应变向量；P为起落架六分量载荷向量矩阵(在结构遵守线性叠加原理的基本假设条件下，可略去式中二次及更高次的自变量项，仅保留一次项，即包含3个力Fx、Fy、Fz和3个力矩Mx、My、Mz的起落架六分量载荷)；A为响应系数矩阵，A中的每个元素为第i个电桥对第j个载荷的响应系数。

通过矩阵运算得到的起落架载荷方程如下：

P=(ATA)-1ATε=Bε

(15)

式中：B为载荷方程系数矩阵。

飞机在地面运行左转弯过程中测得的前轮操纵角和地速如图4所示，该过程中测得的起落架侧向载荷和垂向载荷如图5和图6所示。本文对起落架实测载荷和转弯半径进行无量纲化处理，起落架载荷系数定义为起落架载荷除以飞机质量，转弯半径系数定义为转弯半径除以主起落架前、后支柱之间的距离。

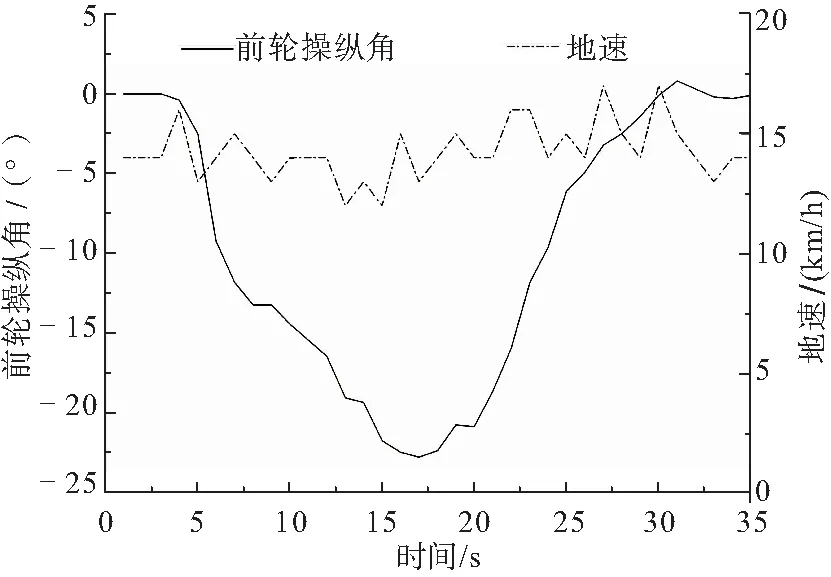
图4 地面转弯飞机状态参数

图5 地面转弯起落架侧向载荷

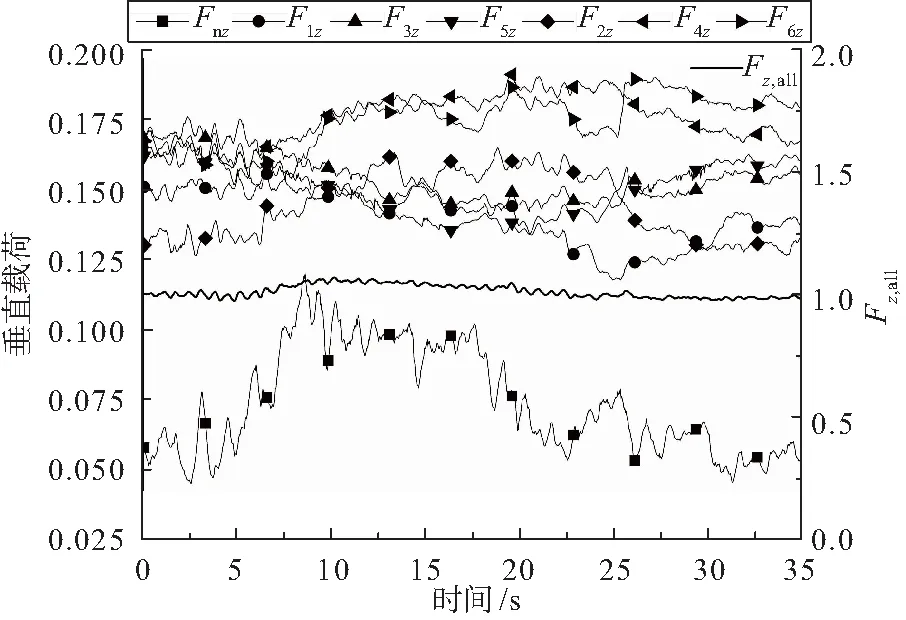
图6 地面转弯起落架垂向载荷

从图5可以看出，左转弯时，主起落架前、后支柱的侧向载荷方向相反，后支柱的载荷方向指向转弯内侧方向，内侧主起落架前、后支柱的侧向载荷最大，前起落架和主起落架中支柱的侧向载荷最小，中支柱侧向载荷不为零，原因是实际转弯中心与理论分析不同，中支柱存在较小的侧滑角。

从图6可以看出，在转弯之前，主起落架前支柱垂向载荷明显小于中、后支柱，这与前支柱缓冲器填充刚度小于中、后支柱的实际情况相符；左转弯时，外侧主起落架垂向载荷略有增大，内侧主起落架垂向载荷略有减小，与上文分析结论一致；所有起落架垂向载荷系数之和约等于1，与实际情况相符。

2.2 侧向载荷预测模型

转弯离心力主要由起落架侧向载荷来平衡，转弯离心力共包括3个要素：转弯速度、转弯半径、飞机质量。其中，前轮操纵角决定了转弯半径的大小。

当采用策略1时，侧向载荷系数可表示为与转弯半径相关的函数，预测模型见式(16)，k1为常数。

(16)

当采用策略2时，侧向载荷系数可表示为与速度相关的函数，预测模型见式(17)，其中k2为常数。

Fy=f(v)=k2v2

(17)

2.3 垂向载荷预测模型

多轮多支柱起落架的初始垂向载荷与缓冲器填充刚度有关，转弯时在倾倒力矩的作用下，外侧起落架垂向载荷分配比例会增大。垂向载荷由初始垂向载荷和倾倒力矩引起的垂向载荷变化量组成，见式(18)。

Fz=Fz0+ΔFz

(18)

与侧向载荷系数预测模型类似，垂向载荷系数预测模型可表示为式(19)和(20)，其中k3、k4、B3、B4为常数。

(19)

Fz=f(v)=B4+k4v2

(20)

2.4 模型参数估计与载荷预测

以第一种策略和内侧主起落架前支柱为例，使用最小二乘法估计式(16)和式(19)的模型参数，得到的侧向载荷、垂向载荷预测模型为：

(21)

(22)

采用均方差和R方估计进行诊断检验，侧向载荷拟合误差为2．7%，R方评估为0．99；垂向载荷拟合误差为0．3%，R方评估为0．98。拟合效果见图7～8。

使用预测模型对最小转弯半径时的起落架载荷进行外推预测，由图7～8可知：r=5时的侧向载荷和垂向载荷的预测值为0.091和0.138。

图7 内侧主起落架前支柱侧向载荷拟合与预测

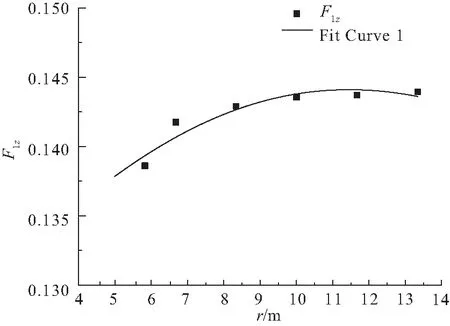
图8 内侧主起落架前支柱垂向载荷拟合与预测

3 地面极限转弯载荷验证

两种策略预测得到的起落架侧向载荷和垂向载荷均小于设计限制载荷的60%，表明载荷设计安全裕度足够，极限转弯试验不会有载荷超限的风险。

分别使用两种策略进行极限状态转弯试验，第一种策略的实测侧向载荷为0.087，预测误差为4.2%；实测垂向载荷为0.135，预测误差为2.1%。第二种策略的实测侧向载荷为0.089，预测误差为4.5%；实测垂向载荷为0.131，预测误差为2.8%。两种策略下的侧向载荷和垂向载荷预测误差均小于5%。

4 结论

1)使用弹性轮胎理论可以定性确定多轮多支柱起落架地面转弯时的侧向载荷方向和相对大小；

2)轮胎侧滑角是产生侧向载荷的主要因素，转弯时主起落架的前、后支柱为严酷受载支柱；

3)多轮多支柱飞机主起落架各支柱的垂向载荷分配与缓冲器填充刚度成正比，且转弯时外侧起落架的分配比例会增大；

4)本文获取的多轮多支柱起落架的地面转弯载荷分配规律可作为起落架结构减重优化和道面剪切强度分析的输入，具有重大的工程应用价值；

5)两种逐步逼近策略的起落架转弯载荷预测模型精度高，可有效减小试飞风险。