龙洗振幅的模拟研究

肖莹莹 丛小涵 杨子涵 叶晴莹

（福建师范大学物理与能源学院，福建福州 350117）

龙洗是古代的一种薄壁盥洗用具，一般为青铜材质，形似现在的脸盆.盆底装饰有鱼纹的，称“鱼洗”；盆底装饰有龙纹的，称“龙洗”（如图1）.龙洗出现的时间，最早可追溯至公元前五世纪，后在唐宋时期逐渐发展成熟.［1，2］该器物最初是工匠为皇宫设计的，后逐渐流传至为民间.图1、图2所示龙洗底部扁平，盆底刻有4条龙，龙口位置位于图2中a、b、c、d4处，盆沿左右两边各有一个把柄，称为双耳（如图1）.龙洗的外观并不复杂，但奇妙之处在于：用手缓慢有节奏地摩擦盆边两耳，盆会像受击撞一样振动起来，盆内水波荡漾；倘若手法得当，4个龙口均可以喷出水花.［3］虽然龙洗的喷水原理已被广泛认可，［4］但对其振动模型的研究却多为定性研究.为了研究龙洗振动的细节，本文结合驻波方程，并利用Matlab建模，［5-8］模拟出龙洗振动幅度的空间分布图像.

图1 龙洗构造图

图2 龙洗的龙口和十字线标注图

1 理论分析

当双手以一定频率摩擦龙洗双耳时，在双耳产生两个方向相反、频率相同的相干波源，两列波相干叠加，呈现出稳定的驻波状态.［9］摩擦时，双手紧挨双耳，双耳可视为固定端，处于波节位置.［9］则根据波的叠加原理，驻波方程为［10］

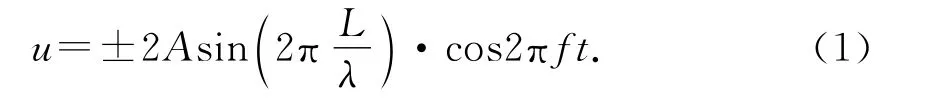
其中，L表示图3中以右耳A点为起点，沿逆时针方向的盆沿长度，λ为波长，f为频率，u为L处的振点偏离平衡位置的位移，φ表示以右耳A点处为起点，沿逆时针方向旋转的角度.

图3 驻波方程参数示意图

由（1）式可知，龙洗模型侧壁振动时的波节和波腹各有4个.［11］实验现象（图4）表明，龙洗喷水范围对称分布在的a、b、c、d4处，此4处即为（1）式中的4个波腹位置，亦即图2中的a、b、c、d4个位置.从图4中可见a、b、c、d之间有4个波节（位于图4中4个白点位置），这一结果与（1）式的结果相符.

图4 龙洗喷水实验

根据驻波形成条件，可知相邻两波节或波腹间的距离为半个波长，可得

其中R为水面半径.

将（2）（3）式代入（1）式可得

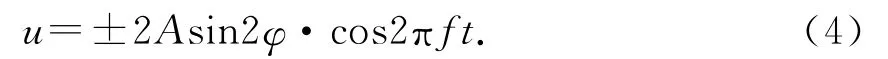
由（4）式可得龙洗各质元随位置变化的振幅函数（其中质元是龙洗洗壁上产生振动的每一个微元）

为了进一步得到不同高度洗壁振幅的关系，利用柱面坐标的波动方程和简化边界条件［12］可解出龙洗喷水时洗壁各质元偏离平衡位置的位移如（6）式所示.这一过程中，为了简化模型，我们将龙洗视为柱形容器.［13-15］

（6）式中b为盆内水体总高度，z为任意水高位置.Am为与角度φ相关的常数项，An为与任意水高位置z相关的常数项.am为φ函数的初相位，与（3）式的φ一致，则

联立（6）～（8）式获得的振幅函数表达式为

与（5）式对比，可发现：当z=b，k=0时，（9）式与（5）式一致，说明（5）式是（9）式的特例，而（9）式是（5）式在空间上的延伸和拓展.

2 模拟方法与模拟结果

采用Matlab 对函数进行模拟.为了方便模拟，计算中取A′=A1／A1max.图5模拟了不同半径（R）的龙洗，侧壁（也称“洗壁”）振幅的空间分布图像，图色的深浅程度与洗壁轮廓上振幅的大小成反比.为方便观察，图5中采用直角坐标系，任意位置到（0，0，0）的水平距离为R.

图5 不同半径R 的洗壁波节和波腹的位置示意图

2.1 龙洗洗壁振幅与半径R 的关系

图6展示的是R=19cm 时龙洗洗壁振幅空间分布的散点图，更方便读者定位龙洗壁沿的波节及波腹位置.

图6 洗壁波节和波腹的位置示意图

2.2 龙洗洗壁振幅与水高z的关系

取b=4.5cm，模拟（9）式可得图7.为了方便模拟，计算中取A″=A2／A2max.从图7 中可以看到，该图完美呈现了4峰振型的现象，且4个波腹处的振幅随着z值的增大明显增大，而波节位置位于图2中十字线位置.

比较图5和图7：图5分析了同一高度、不同半径R的洗壁质元的振动随位置变化的空间分布，得到同一高度的洗壁振幅随半径R的变化图像，进而确定了洗壁振动引起喷水过程的波节和波腹；图7则定量分析了整个系统中洗壁质元随位置变化的三维空间分布图像，不仅明确了龙洗喷水过程中的波节和波腹，并且获得了洗壁振幅随水深的变化情况.由图7 可以发现，不同半径（R）的龙洗，洗壁振幅都具有4峰振型的特征，即波腹波节均有4个，依次交替出现.

图7 龙洗半径R 不同时，洗壁振幅空间分布图像（b=4.5cm）

模拟结果与实验现象（图4）吻合.

为更好地展示龙洗洗壁各质元振幅，我们作了不同z值的振幅分布横向剖面图，图8 为z=1.5cm、z=3.0cm 和z=4.5cm 的振幅分布横向剖面图.对比图8（a）、（b）、（c）发现，振幅的空间分布与图5吻合，且当z=b时［如图8（c）］，模拟结果和实验现象（图4）高度一致.图8中，随着z值增加，各波腹位置的振幅明显增大.且图8各分图中颜色最深位置呈“十”字交叉，此即对应图2 中“十”字交叉位置.

图8 b=4.5cm 时，不同z值的振幅空间分布横向剖面图

从龙洗设计来看，龙洗中“龙吐水”的雕刻位置（图2中a、b、c、d4处）需设计在图8（c）中z=b时对应振幅最大的位置（即波腹位置，亦即图8（c）中a、b、c、d4处）.在没有定量公式和数值模拟的古代，我们的祖先却可以在青铜龙洗制作过程中准确定位“龙吐水”的位置，实在令人叹为观止.

2.3 龙洗洗壁振幅与角度φ 的关系

图9是图7中经过（0，0，0）点平行于z轴的纵剖面图.从图9（b）中可以看出，z取不同值时，φ=90°的振幅都为0，此处即为波节位置.而从图9（a）（c）中可以看出，随着z值的增加，波腹各质元振幅逐渐增大，在z=b时，龙洗洗壁的振幅达到最大值，实验现象（图4）呈现为龙洗的喷水现象.

图9 不同φ 值的振幅空间分布纵向剖面图

2.4 龙洗洗壁振幅与水体高度b的关系

为了研究水体高度b不同时的龙洗振动图像，我们模拟了b分别为1.5cm、3.0cm、4.5cm和6.0cm 的龙洗洗壁振幅空间分布图像，如图10.

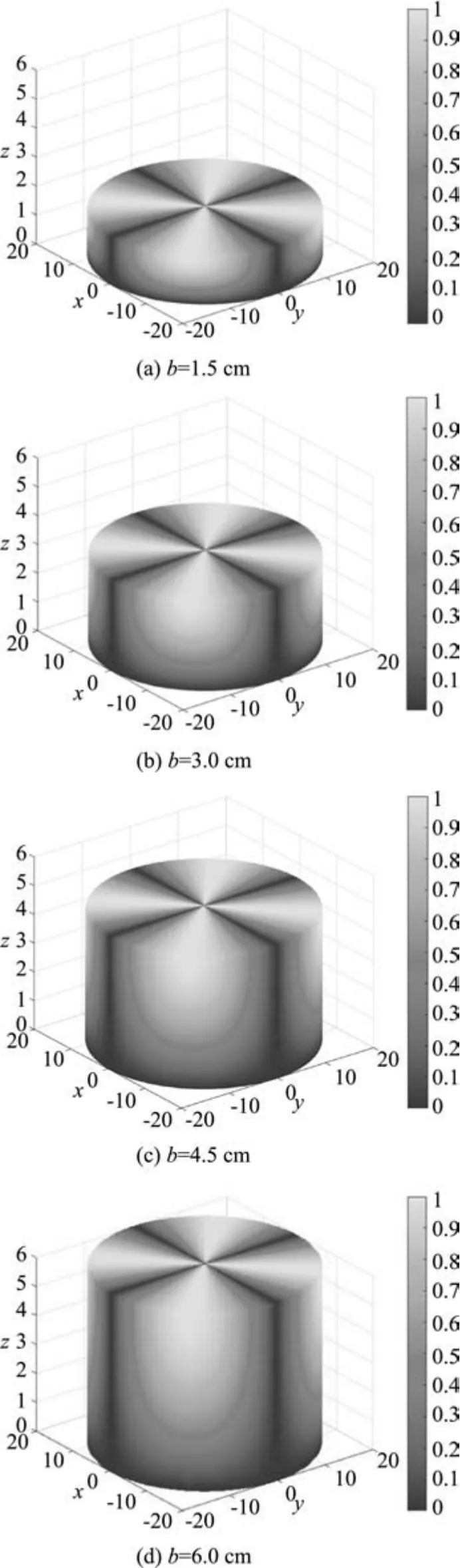
图10 水体高度b不同时，洗壁振幅空间分布图像

比较图10 与图2，可以发现：对于4 节线（4峰）振动的振型，图2中a、b、c、d4点对应图10中不同b值的波腹位置，该处的振幅大于同一水平面的其他位置；4个波节位于图2中十字线位置；对于任意b值，当z=b时龙洗洗壁振幅最大；沿着洗壁，壁沿的振幅呈现出周期性变化，相对振幅如图10所示.

3 结论

通过Matlab模拟，我们可以清晰地看到龙洗洗壁上振幅随空间分布图像，研究发现，洗壁振幅与角度φ和水高z密切相关，其振动为典型的4峰振动，当z=b时洗壁振幅最大.该研究将抽象的龙洗喷水原理转化为形象直观的仿真图，更好地解释实验现象，为龙洗喷水理论和实践研究提供了有效的数据基础.