POE和PBL导向下“弹性碰撞”的深度学习

王贤勇 喻 斌

（贵州毕节市第一中学，贵州毕节 551700）

1 POE和PBL简介

POE教学策略是由Predict（预测）、Observe（观察）、Explain（解释）这3个英文首字母简化组合而成的.该策略是从学生理解科学的探究方法中转演来的，它是建立在“观察渗透”理论哲学观念和建构主义、前概念、概念转变等教育理论基础上的一种教学策略.其基本程序是：创设情境→学生预测→演示观察→（教师引导）学生解释.

PBL 是Problem-Based-Learning 的缩写，它是指以问题为导向的一种教学方法.强调在真实情境中，以学生为主体、教师为主导、问题为导向来展开教学活动.在PBL的学习中，知识的获得来源于对问题认识和解决的过程.［1］以问题为导向，问题本身推动了解决问题和推理技能的应用，同时也激发学生查找信息，以学习关于此问题的知识结构，以及解决问题的方法.其基本程序是：创设情境→提出问题→寻找证据→解释评估.

POE 教学策略和PBL 问题导向学习的共性是以学生为中心，教师只是引导者.之所以要把两者结合是因为：PBL强调的是以问题为导向，即提出（发现）一个有价值的问题是最核心的，然后才是以该问题为导向展开学习，最终要进行评估交流；而POE教学策略注重从实验出发，学生观察实验现象，最后解释实验现象.故POE 和PBL 的融合，有利于培养学生在真实情境中提出问题的能力，有利于提升学生透过现象分析本质的能力，有利于发展学生自主学习的能力，有利于培养学生合作、沟通和交流的能力.二者均是以学生为中心的学习体系，利于培养学生的批判性思维.

2 紧扣教材，由浅入深开展深度学习

如图1和图2所示，教师演示实验：等质量钢球碰撞（先不要告知学生钢球质量相等）.目的是创设真实情境，激发学生学习的兴趣，演示前先让学生进行预测，会看到什么现象.教师开始进行实验演示，如实验2：从一边拉起一个球，由静止释放，另一边就弹起一个球，中间的小球几乎不动；［2］从一边分别拉起2个或3个小球，碰撞之后另一边也相应地弹起等量小球，且振幅相等.学生看到此现象时，安静的教室就像平静的湖面被一块石头激起阵阵的涟漪，学生惊呼、好奇.教师把图3装置按小组发给学生，让学生自己演示、体验、观察，然后提出问题.最后教师收集学生问题，经过筛选、提炼出核心问题.即该实验的本质是什么，并确定为探究学习的主题.

图1 弹性碰撞演示装置

图2 弹性碰撞演示装置

图3 弹性碰撞演示装置

2.1 数学推演与结果分析

以教材为例，学生自主学习弹性碰撞的概念，教师引导学生构建物理情境.如图4，光滑水平面上，一个质量为m1的小球以速度v1与一个质量为m2的静止小球发生弹性正碰，分析碰后两球的速度.教师巡查课堂，引导学生解答问题，题目涉及的原理和方法有：动量守恒、动能守恒、解方程组，针对不同小组提示的关键词不尽相同.

图4 弹性碰撞模型

学生解出碰撞后两小球的速度分别为

小组交流评估：若m1=m2时，v1′=0，v2′=v1；若m1≫m2时，v1′=v1，v2′=2v1；若m1≪m2时，v1′=-v1，v2′=0.

教师引导：学生们的数学分析结论是否正确，需要用实验来进行验证.

学生论证：对m1=m2的验证，给学生提供天平，让学生自己测出实验小球的质量，发现小球质量相等，当碰撞满足动量守恒和机械能守恒定律时，小球能量交换.再根据对称性，推导出左右摆动的小球数目相同、振幅相等，这就是开始学生们看到的图1和图2的实验现象.

对m1≠m2的验证用图5 的实验装置来完成.教师指导学生把气垫导轨调节水平，［3］教会学生读取、记录光电门的读数，然后由学生自行选择满足两种情况下不同质量的滑块来完成实验论证.

图5 气垫导轨验证弹性碰撞

教师总结：学生们理论计算得出的结果和实验结果是一致的，证明理论是可靠的.学生们如果进行类似的探究学习，也可采用相同的方法.

而究其原因，是单爷最会攥弄书道子（评书底本），他能把不同的几个故事套子一拼接，就能编出一部新书来。一部《白眉大侠》以前不是接在《三侠五义》故事的后面，但他梳理了人物关系，把《三侠剑》的书道子挪到这里用，而到真说《三侠剑》时继续编新的。他能从徐良这一辈的侠客，说到各门各派祖师爷那里，前后能说出五六代人，最后出场的人物都有一百岁的老剑客。里面的人名和绰号都疯了：铜金刚铁罗汉磨成大力佛欧阳普中、横推八百无对手轩辕重出武圣人于和于九莲……但每位剑客的形象、性格、武功、兵器、为人都十分鲜明，这足令写小说的羞愧。而这还算完，他还给续了个《龙虎风云会》，几乎是白眉大侠的“同人小说”。

2.2 模型建构与推理论证

学生们经历了上面的学习之后，对弹性碰撞已经有了初步的认识.提升学习深度，如果图4中的m2是以v2向右运动的，其中v1＞v2，又如何分析碰撞后两球的速度呢？笔者巡查课堂发现，学生依然从解方程的思想来思考问题，而且很多小组很快推导出

此时引导学生把得出的（3）式进行移项，变为

分析（4）式得出：发生弹性碰撞的过程中，球1靠近球2的速度等于球2远离球1的速度，可简单总结为碰撞过程相对速度相等.为了加深对（4）式的理解，尤其是速度矢量性的理解，在此处增加一个例题.

例1.如图6，质量为m1的小球与质量为m2的小球发生正碰，碰撞时间极短，两球碰撞前后的速度-时间图像如图7，下列说法正确的是

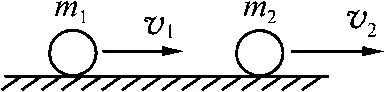
图6

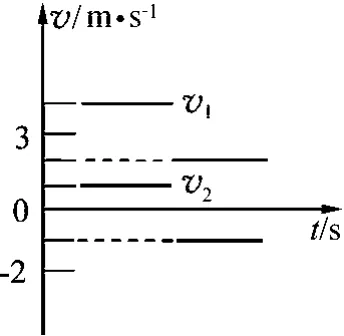
图7

（A）碰撞过程动量不守恒.

（C）该碰撞为弹性碰撞.

（D）两球的质量关系满足3m1=m2.

要求学生在1min之内完成分析.笔者在课堂巡查中发现，很多学生依旧从动量守恒和动能守恒的角度来进行分析，1min之内根本分析不出结果.但小组内已经有学生利用（4）式来分析问题，此时教师再给学生们2min时间，要求学生们在组内展开讨论，优化解决问题的方法.笔者继续巡查课堂，适度参与一些“问题小组”讨论，注重引导，例如（4）式成立的条件是什么，与质量有关吗？在笔者的引导之下，学生们很快总结出了（4）式的物理含义：与物体质量没有关系，并且能够快速判断碰撞是不是弹性的.

经过讨论发现，学生对（4）式的理解还不够深刻，尤其是对相对速度相等的理解还是处于一知半解的状态.继续引导学生深度学习：发生弹性碰撞的过程中两球的形变是先增大后减少.为了便于学生理解，构建如图8 的模型，表述为：小球2与一轻质弹簧连接，小球1从接触弹簧开始，弹簧形变逐渐变大，当两球共速时形变最大，然后弹簧逐渐恢复原长，最终两球分离.

图8 弹性碰撞的过程模型

从接触到弹簧形变最大的过程中，弹力从0到最大；从弹簧形变最大到两球分离的过程中，弹力从最大减小到0，因此弹力的变化具有对称性；选小球2为参考系进行观察，小球1 先向右运动靠近小球2，然后再向左运动远离小球2，运动具有对称性；小球1的相对平均加速度不变，所以靠近和远离的时间不变，时间长短亦具有对称性.教师应充分挖掘出这3 个特点，引导学生体验物理学的对称之美.让学生在同一坐标系（以地面为参考系）中尝试作出两球运动的速度 时间图像，最后教师提供图9以供参考.

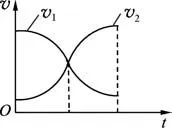
图9 弹性碰撞速度时间图像

通过图8 和图9 的学习，让学生继续分析两球分离时的速度.在课堂巡查中笔者发现，绝大部分学生还是运用解方程组的思路来分析问题.笔者继续启发学生从对称性的角度出发，将弹簧形变最大的状态作为桥梁，把两球靠近和分离的过程连接起来.经过引导，学生推导出

对球1有

对球2有

由（5）式和（6）式的关系推知，在（3）式中始终满足v1+v1′=v2+v2′=2v共.

在弹簧与小球接触到弹簧形变最大的过程中，由动量守恒有

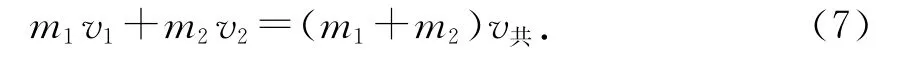
联立（5）～（7）式可得

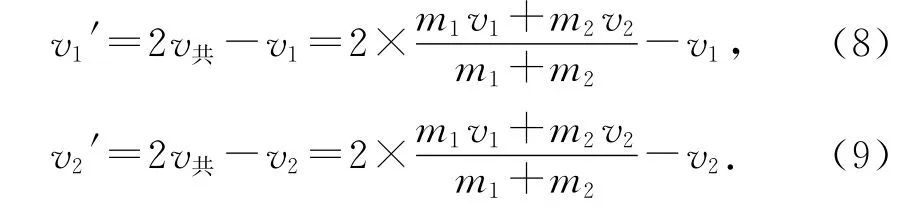
为了验证（8）式和（9）式的正确性，笔者首先让学生从v2=0的特例出发，求解出碰后两球的速度，学生经过分析，发现结果与（1）式和（2）式完全相同，证明了（8）式和（9）式的分析过程和结果都是可靠的.接下来笔者再让学生继续从解方程组的思想来求解，最后的结果也是与（1）式和（2）式完全相同的.笔者发现此时学生的脸上洋溢着笑容，目光中充满了成就感和喜悦之情，犹如孩子突然得到期盼已久的玩具一样快乐.有一个学生在小组评价中这样说道：这种分析方法绕开了复杂的数学运算，犹如拨开云雾见阳光，真是“山重水复疑无路，柳暗花明又一村”，妙哉，妙哉！这样的课堂教学，抓住了物理是透过实验悟理的本质，可谓格物致知.让学生体验到了物理的对称之美、情境之韵，参考系选择之巧、力和运动结合之准、动量与能量相结合之妙.

3 总结提升

笔者利用POE 教学策略和PBL 问题导向，开展了一次对弹性碰撞深度学习的尝试，流程归纳如图10.

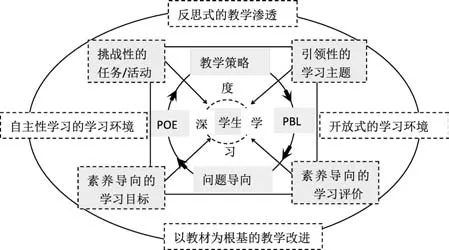
图10 POE和PBL相结合的教学流程

对图10流程的导读：POE教学策略和PBL问题导向下的深度学习，其根本特点是以学生为中心，以教材为基础.在开放式和自主式的学习环境中，创设真实情境（实验），以学生预测、观察，寻找有价值的问题为导向，致力于激发学生学习的兴趣和动机.深度学习是学生在教师的引导下，通过对知识的理解和创造，实现自身认知结构完善、关键能力发展和素养提升的过程.［4］作为教师，更重要的是引导学生提出有挑战性、引领性的问题，同时把问题导向物理核心素养目标、把评价导向素养评价，吸引学生主动地、聚精会神地投入学习之中，让学生真正回归学习主体的角色，从而感受学习的乐趣，体会学习的价值和意义，在学习中收获成就感和效能感，进而达到热爱学习、理解规律、学以致用的目的.