反向等价转化证明不等式

山东省邹平双语学校(256200) 姜坤崇

山东省邹平市教学研究室(256200)莫静波

将所证的不等式等价转化是证明不等式的基本策略和方法.对于一个不等式的证明,按其不等号的方向来说,一种是按原来所给的不等号方向来证明,再一种就是将其等价转化为相反方向的不等式来证明.对于某些不等式,若按原来的不等号方向证明较为困难,而改为证明与之等价的反向不等式,则比较容易,下面举出若干例子说明这一策略和方法的具体应用.

一、证明条件不等式

所谓条件不等式,是指含有某种约束条件的不等式,如三个正数a,b,c满足条件式a+b+c=1,abc=1,等等.

(1)式即为与原不等式等价的反向不等式.由条件式a+b+c=1 及三元均值不等式得

即(1)式成立,故原不等式得证.

例2(自编题)已知a,b,c是满足a2+b2+c2=3 的正数,求证:

证明

证法1转化为证明原不等式的反向等价不等式

令a=x2,b=y2,c=z2(x,y,z ＞0),则(xyz)2=abc=1,于是由柯西不等式的变形

即(3)成立,从而待证不等式成立.

证法2先证明原不等式的反向等价不等式(3)成立.

说明将欲证不等式等价转化为反向不等式,为使用柯西不等式创造了条件.以下例5、例10-14 等的证题思路亦如此.

例5(自编题)设a,b,c ＞0, 且abc=1, 求 证:

证法1转化为证明原不等式的反向等价不等式

原文提供的证明较繁,下面证其反向等价不等式则较易.

因为a2+1=a2+ab+bc+ca=(a+b)(c+a),同理b2+1=(b+c)(a+b),c2+1=(c+a)(b+c),于是以上不等式等价于

由于最后一个不等式显然成立,故原不等式成立.

证法2同证法1,问题转化为: 已知ab+bc+ca=1,证明

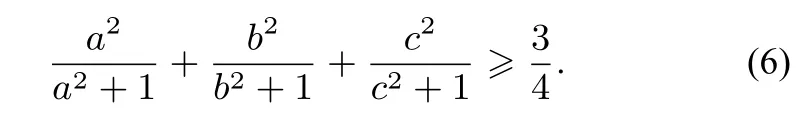
由于(a+b+c)2=a2+b2+c2+2(ab+bc+ca)=a2+b2+c2+2,故由柯西不等式的变形式得

证法2

以上不等式即为不等式①,下证从略.

证法3

这正是例6 中的不等式,即知所证不等式成立.

即(7)式成立.所以原不等式成立.

例9(IMO2005)正实数x,y,z满足xyz≥1,证明:

由柯西不等式及题设条件xyz≥1,得

故原不等式成立.

二、证明无约束条件不等式

这类不等式除了所给变元是正数的条件之外没有其它等式的约束条件.

而由柯西不等式的变形式得

所以原不等式得证.

由柯西不等式的变形式得

故原不等式得证.

例12(自编题)设a,b,c为正实数,求证:

证明

例13(自编题)设a,b,c为正实数,k为常数,k≥2,求证:

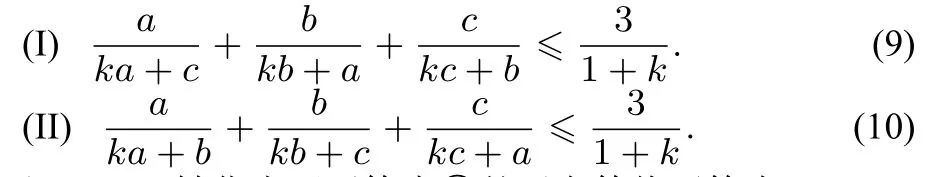
证明(I)转化为证不等式④的反向等价不等式

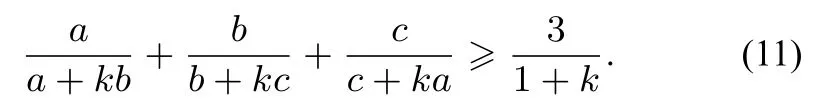
由柯西不等式的变形式得不等式(11)的左边等于

又因为

(II)先证不等式(10)的反向等价不等式:

不等式(12)的证明仿不等式(11)的证明可证,从略.

又因为

(II)仿(I)的证明先证明不等式:

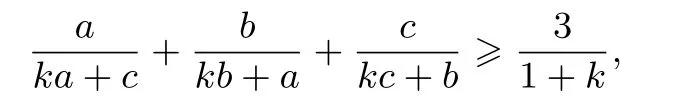
然后由此不等式可证得不等式(14)成立,限于篇幅,证明从略.