探究四类数列不等式证明题的一般性解决策略

广东省东莞外国语学校(523430) 黄 威

一、形如数列不等式

例1(2022年新高考I卷第22 题)已知函数f(x)=xeax-ex.

(1)当a=1 时,讨论f(x)的单调性;

(2)当x ＞0 时,f(x)＜-1,求a的取值范围;

(3)设n ∈N*,证明:

综上所得,原不等式成立.

例2(2019年高考浙江卷第20 题)设等差数列{an}的前n项和为Sn,a3=4,a4=S3, 数列{bn}满足: 对每n ∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列.

(1)求数列{an},{bn}的通项公式;

综上所得,原不等式成立.

二、形如＜f(n)(ai ＞0)数列不等式

例3(2020年高考新课标Ⅱ卷理科第21 题)已知函数f(x)=sin2xsin 2x.

(1)讨论f(x)在(0,π)上的单调性;

(3)设n ∈N*, 证明: sin2xsin22xsin24x···sin22nx≤

分析(1)略.(2)|f(x)|≤(过程从略).(3)

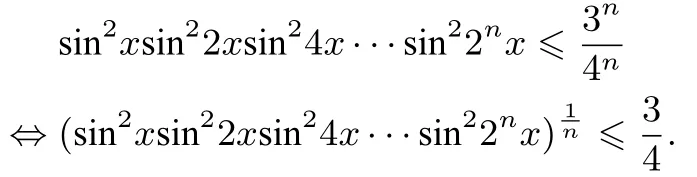
注意到不等式左边可以看作数列{an}的前n+1 项积,an=sin22nx,这并不是形如＜c(c为常数)数列不等式证明题,因此,问题的关键在于将不等式左边前n+1项积转化为前n项积形如＜c(c为常数)数列不等式证明题.

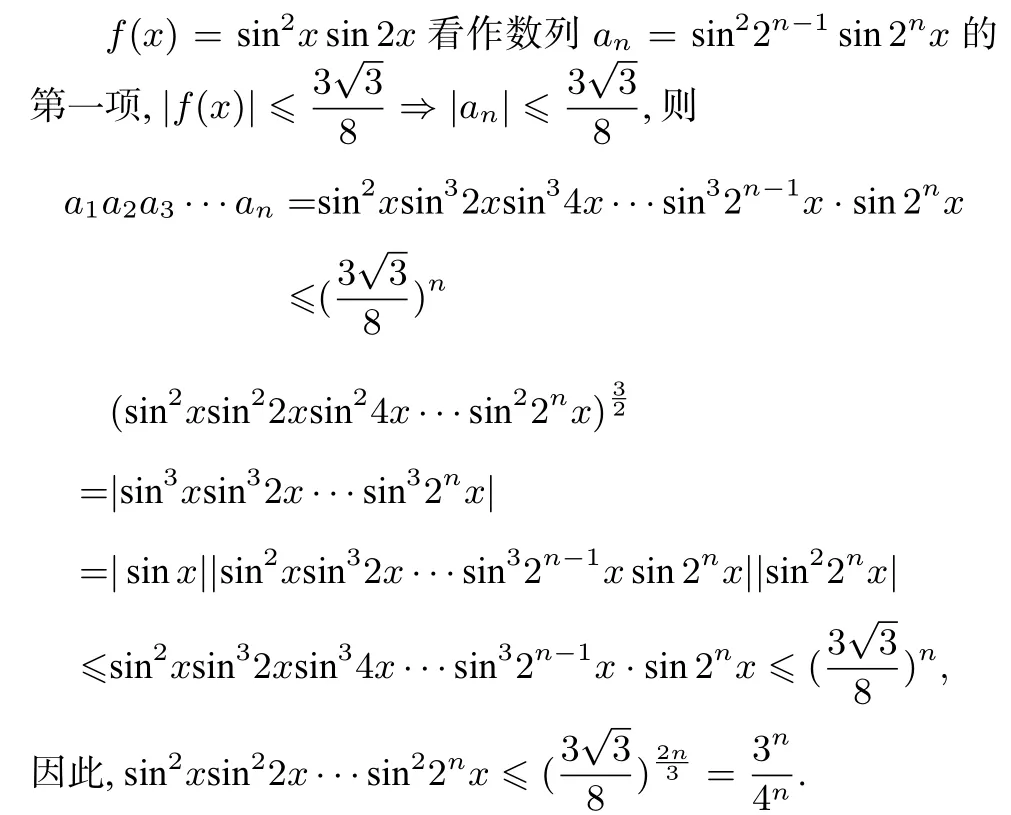
本质上,将不等式左边放缩为

例4(2009年高考山东卷第20 题)等比数列{an}的前n项和为Sn, 已知对任意的n ∈N+, 点(n,Sn), 均在函数y=bx+r(b ＞0 且b≠1,b,r均为常数的图像上.

(I)求r的值;

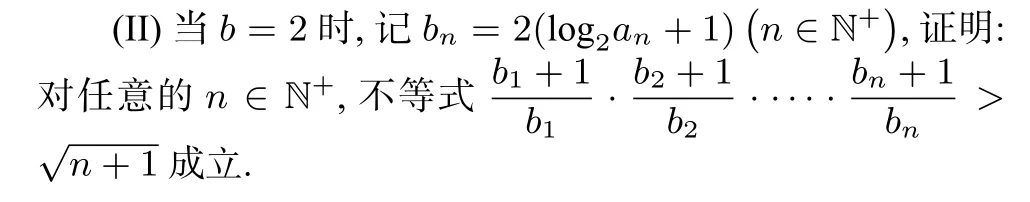
解(1)r=-1.(过程从略)

综上所述,可得不等式恒成立.

例5已知函数

(1)求函数f(x)的极值;

(2)(i)当x ＞1 时,f(x)＞0 恒成立,求正整数k的最大值;

(ii)证明: (1+1×2)(1+2×3)...[1+n(n+1)]＞

解(1)略;(2)(i)正整数k的最大值为3.(过程从略)(ii)证明: 两边取对数得

综上所述,可得不等式恒成立.

三、形如 ＜c(c 为常数)数列不等式

例8(2012年高考广东卷)证明: 对一切正整数n, 有