切向加载下螺栓连接复合板的失效分析*

杨 洋 刘文光 王晓婷 宫明光 郭 浩 汪 杰

(1.南昌航空大学航空制造工程学院 江西南昌 330063; 2.江西洪都航空工业集团有限责任公司 江西南昌 330024)

随着复合材料在飞机上的大量应用，其强度问题受到广泛关注，为此，研究人员针对不同复合材料提出了40多种强度准则。但由于复合材料破坏机制十分复杂，破坏模式众多，尚无一种强度准则完全适用于所有材料[1-2]。目前应用较为广泛的失效准则主要包括最大应力准则、Tsai-Wu张量失效判据、Puck失效准则、改进后的Hashin失效准则等[3]。

围绕螺栓连接复合板的失效问题，研究者开展了大量的研究。针对Tsai-Wu失效准则，ARRUDA等[4]通过等效应力应变改进了该准则无法识别损伤是否位于纤维、基质或层间区域的问题。基于刚度矩阵退化和Puck失效准则，BEK等[5]模拟和验证了复合层合板拉伸试验中渐进损伤的过程。王佩艳等[6]采用最大应力准则、Hashin失效准则及其混合准则分析复合材料机械连接件的三维累积损伤，发现最大应力准则适合于拉伸破坏为主的结构，而Hashin准则适合于剪切破坏为主的结构。应用板壳单元，边天涯等[7]建立了螺栓连接复合层合板的有限元模型,研究了铺层方向及铺层比例对接头挤压强度的影响。通过分析位移载荷响应以及纤维与基体破坏层显微形貌，KHASHABA等[8]研究了钉孔间隙尺寸吸收的失效能及其对延缓失效的作用。基于位移载荷响应与断层形貌，KELLY和HALLSTRÖM[9]研究了横向载荷对螺栓连接复合层合板破坏模式的影响，分析了复合层合板的层间剪切失效行为。采用不同单元模拟复合材料失效，LIU等[10]探索了二次弯矩效应对螺栓接头连接强度的影响。

与金属材料螺栓接头的力学特性相比，复合螺栓接头的力学特性更为繁杂。加之开孔和各向异性引起的应力集中，螺栓接头成为复合结构最为薄弱位置[11]。螺栓孔不但缩小了结构静承载面积，而且破坏了结构的连续性，导致孔的周围应力分布状态复杂化[12]。因为复合材料是一种由不同相构成的脆性材料，所以材料在到达破坏极限之前不会出现局部屈服，无孔周载荷重新分配的能力[13]。另外复合材料是一种各向异性材料，纤维和基体的融合使其在微观上呈现不均匀性，加剧了孔周局部应力集中程度[14-15]，导致螺栓接头的失效模式复杂，强度预测更加困难[16]。

目前，研究人员对螺栓连接复合板的失效预测做了很多工作，但是对孔周应力集中损伤过程以及损伤位置的确定等问题尚未厘清。本文作者结合改进的Hashin准则，应用基于Python语言的ABAQUS有限元软件的二次开发技术，建立了螺栓连接复合板的损伤失效过程模型，讨论了其结构的位移载荷响应及孔周应力分布规律。

1 基本理论

复合板失效分析的理论基础是基于Hashin准则精确预判各种失效模式和程度，并结合材料刚度折损判定模拟渐进损伤过程，进而预测螺栓连接复合板的损伤部位及破坏强度。

复合层合板三维材料本构关系模型[17]为

σ=Cε

(1)

式中：σ表示应力向量；C表示刚度矩阵；ε表示应变向量。

各向量和矩阵的表达式为

(2)

(3)

(4)

式中：σij表示应力分量；εij表示张量剪应变;Cij表示刚度系数,i,j=1,2,3。

各系数的具体表达式为

(5)

式中：Ei表示主方向的弹性模量;Gij表示主平面的剪切模量;νij表示主方向的泊松比；i,j=1,2,3。

改进的Hashin失效准则[18]所包含的破坏模式较为全面，包括纤维拉伸及压缩失效、基体拉伸及压缩失效、纤维基体剪切失效和分层失效。各失效模式的判断准则如下：

(1)纤维拉伸及压缩失效准则FV1

(6)

(2)基体拉伸及压缩失效准则FV2

(7)

(3)纤维基体剪切失效准则FV3

(8)

(4)分层失效准则FV4

(9)

式中：S12、S13、S23分别表示面内剪切强度；XT、XC、YT、YC、ZT、ZC分别表示纤维拉伸强度、纤维压缩强度、基体拉伸强度、基体压缩强度、板厚拉伸强度、板厚压缩强度。

复合板在切向加载失效时，每个单元都会出现以上4种破坏模式组合而成的某种失效状态。为了便于模拟复合板的损伤情况，表1给出了复合材料失效状态材料属性突降的设置情况。方程(6)—(9)给出了预测螺栓连接复合板的失效准则。因此，借助Abaqus软件中的子程序，可以定义材料的基本力学性能参数、本构关系、失效准则和刚度折损判定等参量，并按照图1所示的流程预测螺栓连接板的失效模式和损伤演化分析。

表1 材料属性突降准则

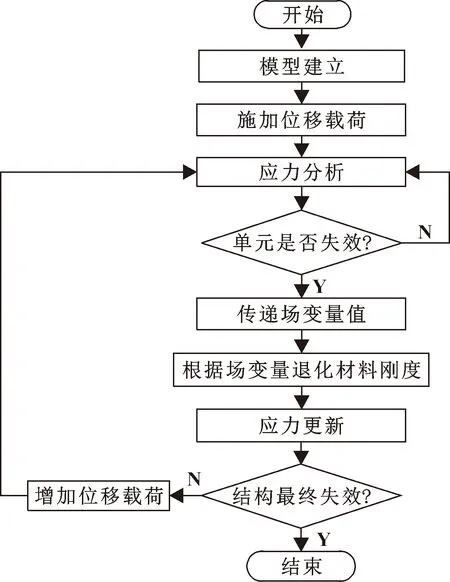
图1 渐进损伤模型计算流程

2 复合螺栓接头的有限元建模及验证

复合螺栓结构由2块相同的复合板和3个M8螺栓构成。结构几何形状及尺寸如图2所示。复合材料的铺层为37层，按0°和90°交替铺层，单层厚0.135 mm，螺栓与板的端距比E/D为3，宽径比W/D为6。表2所示为复合材料板的力学性能参数。

表2 复合板材料的力学性能参数

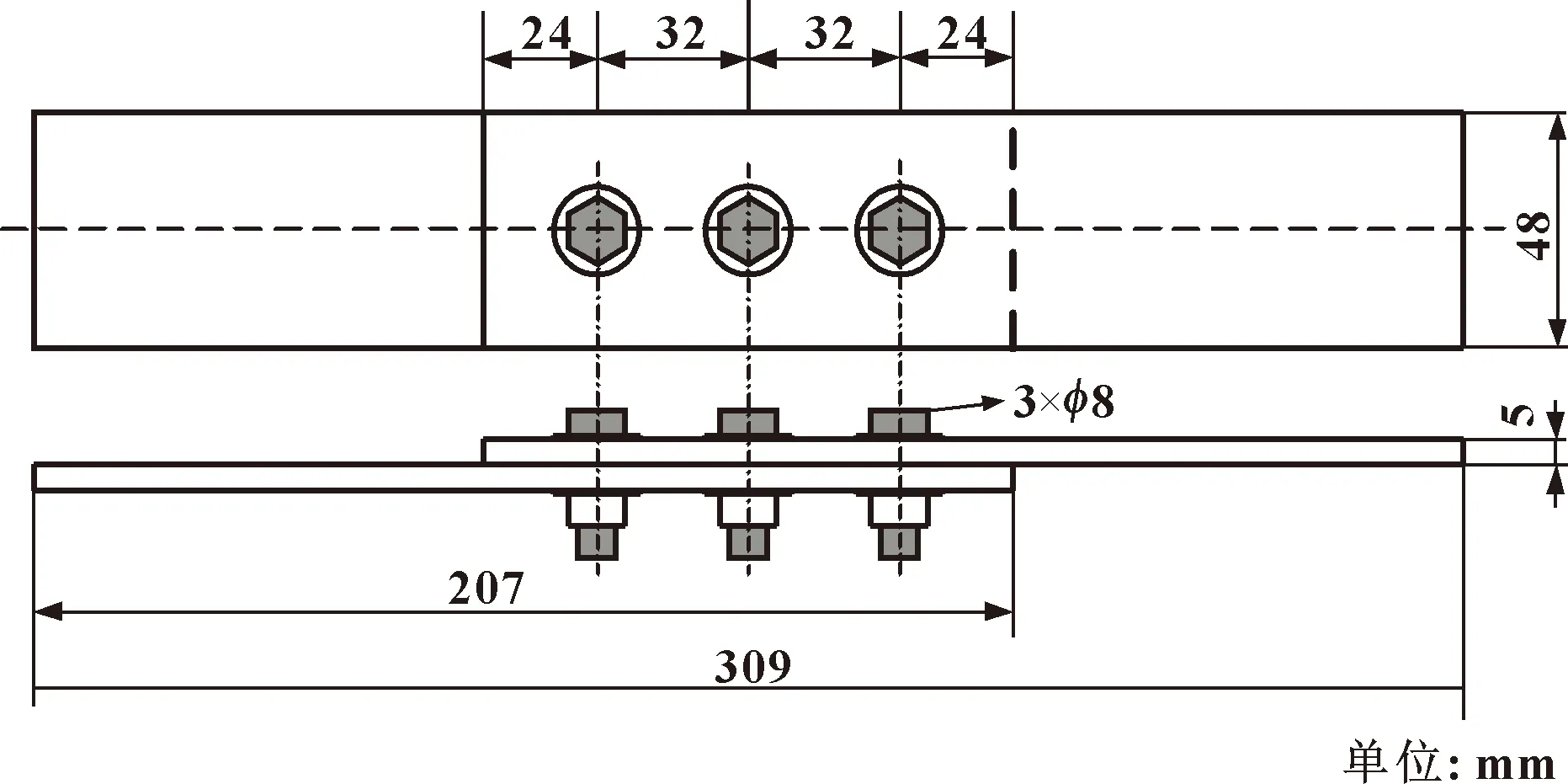
图2 几何模型

依据几何尺寸和材料属性，建立图3所示的复合螺栓接头有限元模型。复合板、螺栓均采用8节点六面体线性减缩积分单元C3D8R。每层划分一个单元，复合板全局种子大小设为4，螺孔周围网格加密，种子大小为2，螺栓种子大小为1。由于复合板为对称结构，取1/2模型进行分析以降低运算成本。将螺栓、螺母及垫圈简化为整体，复合板的界面摩擦因数设为0.2。约束螺栓连接板的下板的6个自由度，1/2模型横截面上设置关于y轴对称的边界条件。

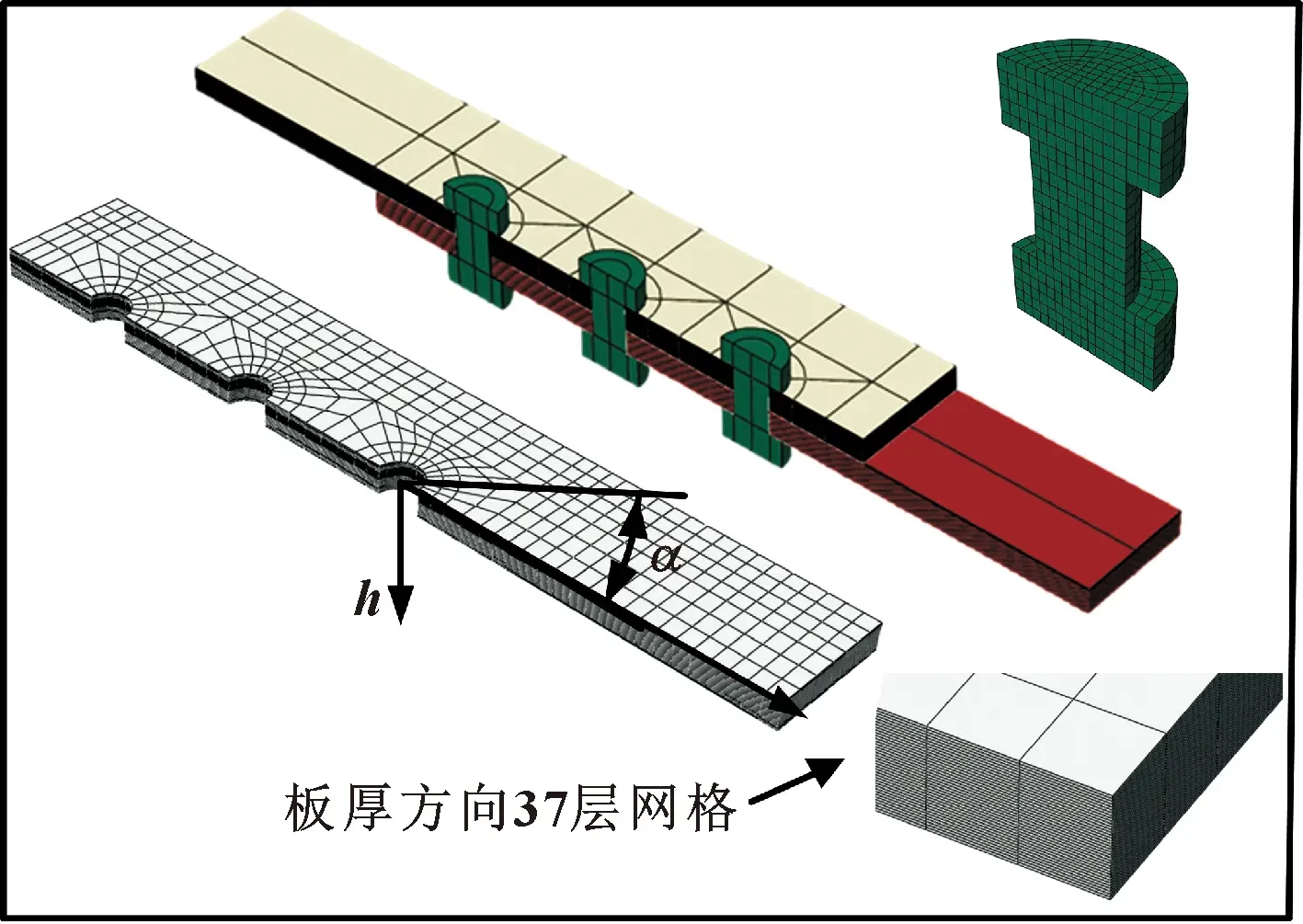
图3 有限元模型

采用降温法给螺栓施加预紧力[19]，等效温差与预紧力的关系为

(10)

式中：ΔT为等效温差;E33为复合板厚度方向的弹性模量;Eb为螺栓弹性模量；α为线性膨胀系数;l为螺栓所连接的有效长度。

根据机械设计理论[20]，螺栓所加载的预紧力和预紧力矩的关系为

T0=K·Dd·F0

(11)

式中：T0表示施加的预紧力矩；K为紧固系数；Dd为螺纹的公称直径;F0为预紧力。

为便于研究，由方程(11)求得0.5、5和10 N·m预紧力矩对应的预紧力。假设初始温度为0 ℃，由方程(10)将温度载荷施加于螺栓杆，求得最终温度设置为-163、-1 629.8、-3 259.7 ℃。根据有限元模型，可求出切向加载下螺栓连接复合板的位移载荷响应，并与试验结果比较，如图4所示。

图4 位移载荷响应

图4表明，损伤失效模型对连接强度具有很好的预测性。表3列出了螺栓连接复合板的极限载荷与极限位移，表中Fmax和Umax为接头试验测得的极限载荷和极限位移，fmax和umax为仿真得到的极限载荷和极限位移，两者误差均小于10%。

表3 试验结果与模拟结果误差分析

3 分析与讨论

引起螺栓连接复合板失效的因素很多，下面着重讨论接头的极限载荷和孔周应力分布。

3.1 预紧力矩对极限载荷的影响

保持螺栓与板间的摩擦因数为0.2，复合板间摩擦因数μ和预紧力大小如表4所示。图5示出了复合板间摩擦因数为0.42时，不同预紧力下的位移载荷响应。

表4 不同预紧力及摩擦因数下的极限载荷Fmax

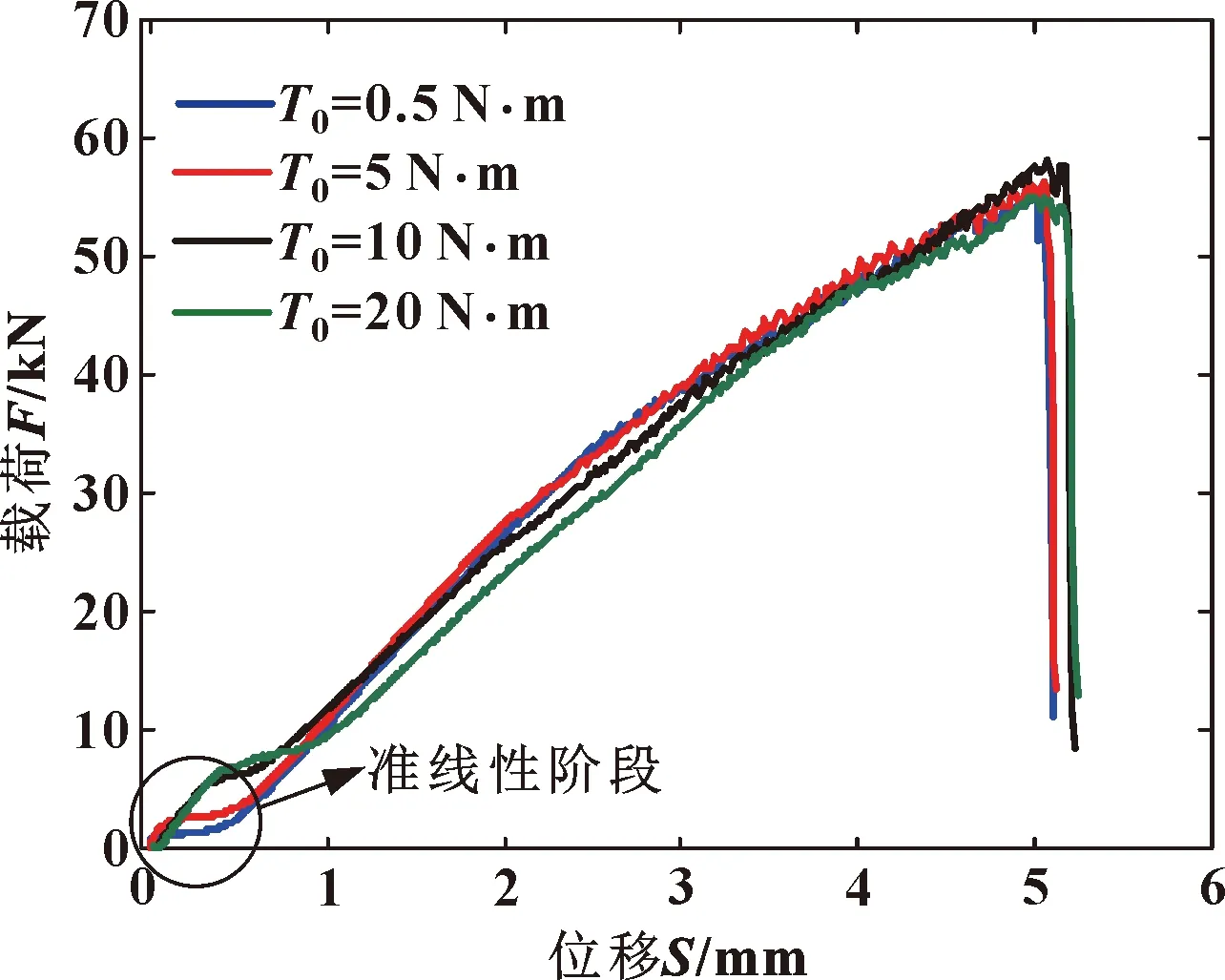
图5 不同预紧力下的位移-载荷曲线

结果表明，当复合板界面间的摩擦因数分别为0.1、0.2和0.42，而预紧力矩由0.5 N·m增加至10 N·m时，极限载荷分别增加4.9%、5.1%、5.1%；如果预紧力矩继续增至20 N·m，极限载荷则下降。究其原因，这是由于过大预紧力而产生的接触压力致使复合板提前出现损伤。因此，选择合适的螺栓预紧力矩，有利于提高极限载荷。当复合板间摩擦因数为0.42时，预紧力对准线性阶段的位移载荷响应以及极限载荷值有明显影响。而当预紧力相同时，随着摩擦因数增大，极限载荷均出现微量上升；当预紧力足够大时，摩擦因数对极限载荷的影响甚微。

3.2 孔隙对极限载荷的影响

表5和图6示出了复合板摩擦因数为0.2、预紧力矩为10 N·m时，不同螺栓孔间隙对连接板位移载荷响应的影响。

表5 孔隙对极限载荷的影响

图6 不同孔隙下的位移-载荷曲线

结果表明，准线性阶段，不同孔隙的位移载荷响应基本保持一致，孔隙对极限载荷的影响主要体现在滑移阶段及剪切变形阶段；随着孔隙的增加，极限载荷持续下降，孔隙从0增至400 μm，极限载荷下降约9%。这是因为孔隙的增大会减小螺栓与螺孔间的有效接触面积，从而影响螺栓连接的压力分布和强度。

3.3 铺层角度对孔周应力的影响

由于复合材料的铺层对孔周应力有不可忽视的影响，文中基于图3所示坐标系分析了0°铺层与90°铺层时，螺栓孔周应力随着角度和深度的变化情况。考虑不同方向应力，分别研究了总应力σ和应力分量σ11、σ22、σ33的分布情况。文中将位置角θ位于区间[0°，90°]的区域定义为受横向拉伸载荷螺栓连接板的承压区域。

图7示出了0°铺层和90°铺层时孔周等效应力的变化。结果表明，随孔周角度变化，应力值在90°达到最大值，呈现先增大后减小趋势，且承压区域应力均大于非承压区。应力值随深度的波动规律趋于一致，呈递增趋势。因此，应力随深度的变化情况对材料铺层有重要指导意义，即在承受较大应力的深度需增加0°方向的纤维铺层。

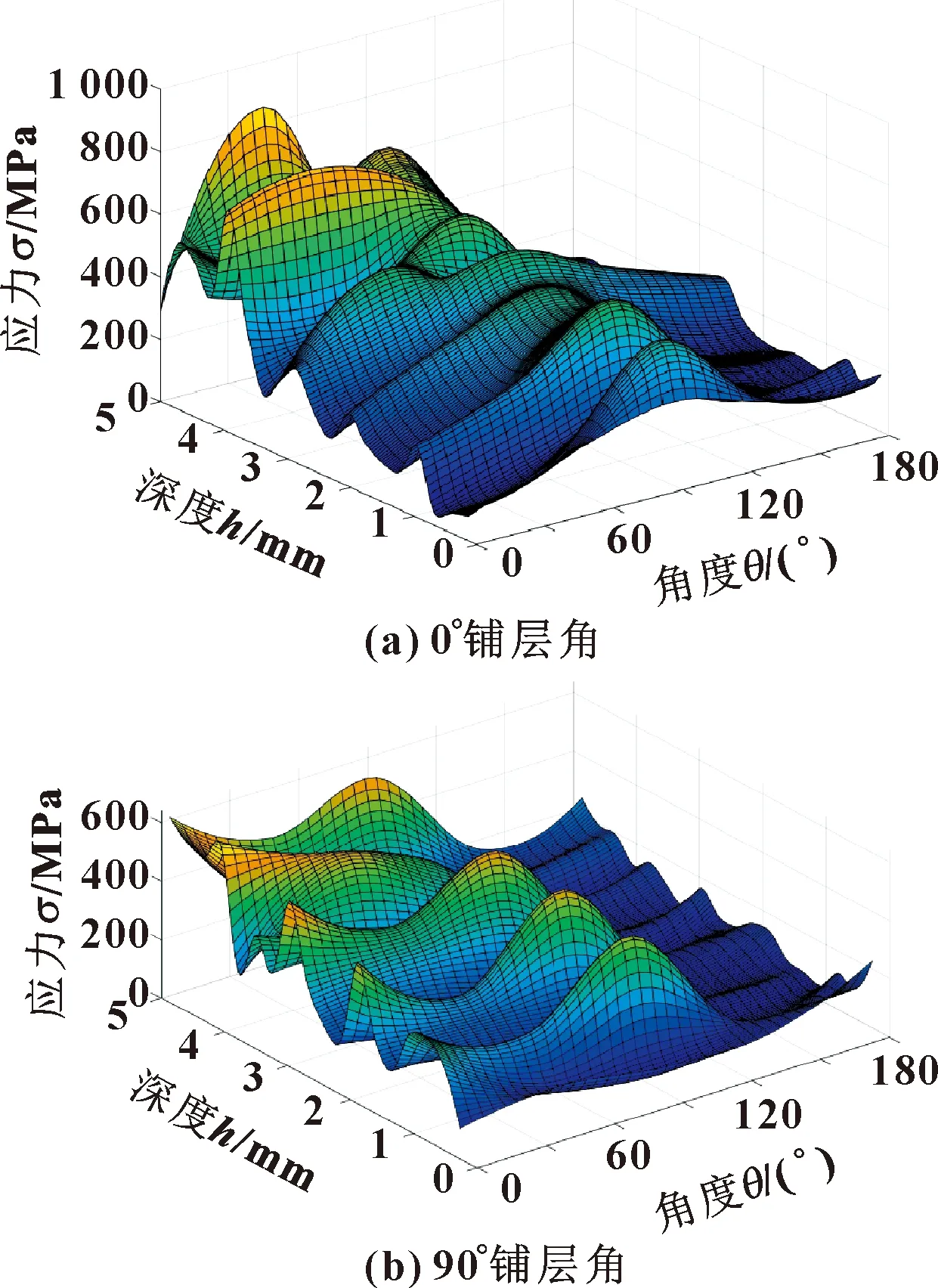
图7 孔周等效应力

图8示出了0°铺层孔周的主应力σ11、σ22、σ33的分布情况。位置角θ在[0°,45°]区间内，σ11均为压应力，这是由于孔壁挤压，且随着单元深度位置逐渐靠近界面，压应力值逐渐增大。位置角θ在[90°,180°]区间时，单元应力值为正，随着位置角度及位置深度的变化，应力值变化甚微。由于σ22应力分量方向与90°纤维铺层方向相同，减少了应力的变化趋势，所以90°铺层时应力分量σ22的波动范围小于0°纤维铺层。当铺层角度为0°时，随深度位置变化，应力无明显变化趋势。

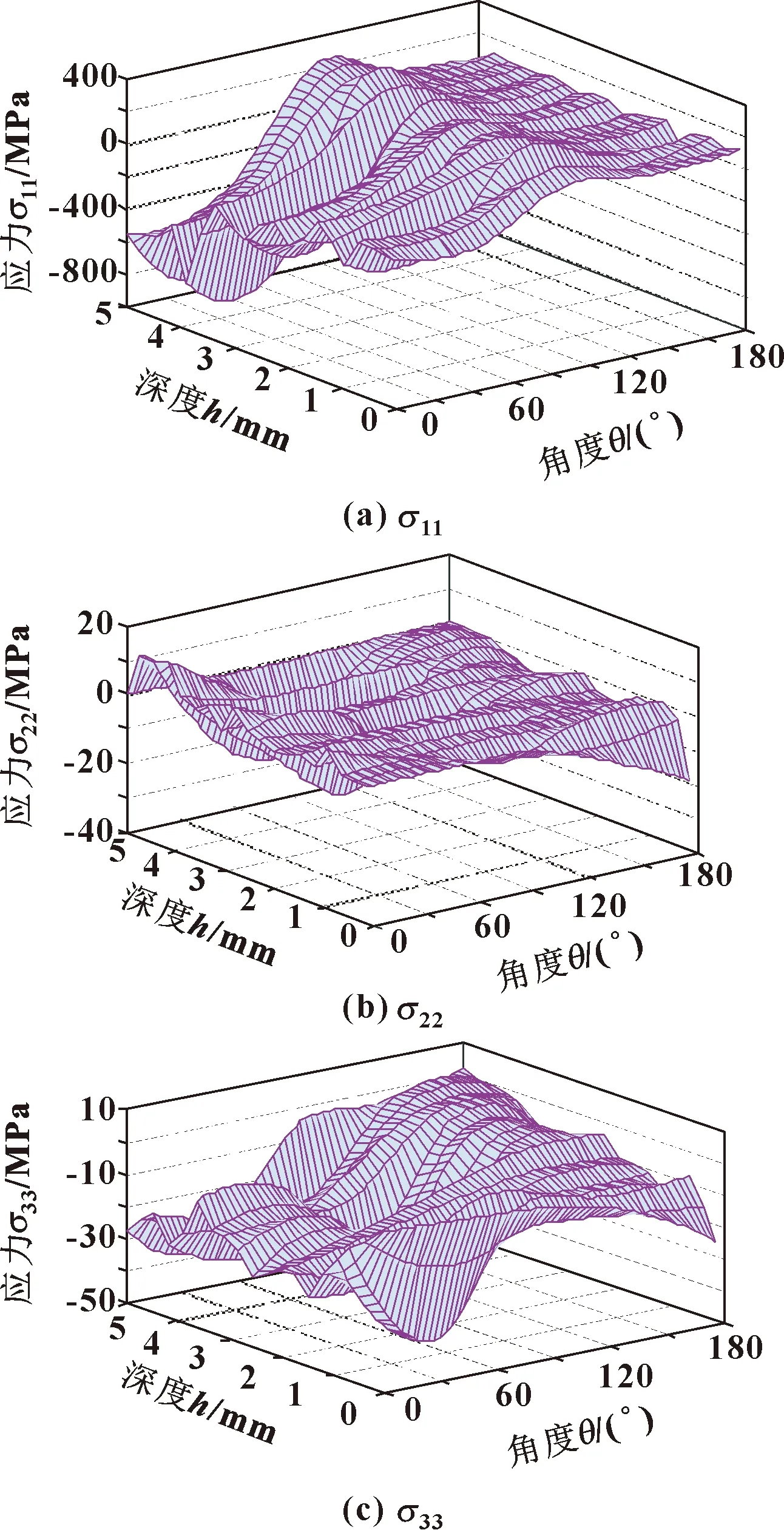
图8 0°铺层角时应力分量

如图9所示，铺层角α= 90°时，σ11应力从正值变化至负值并在90°时达到最低；σ11应力随θ增大而减小,随着位置深度的增大而减小。θ从90°变化到180°，应力无明显变化。当纤维铺层角度为90°时，应力值随深度位置几乎无变化，而随着角度位置总体呈单调递增趋势。

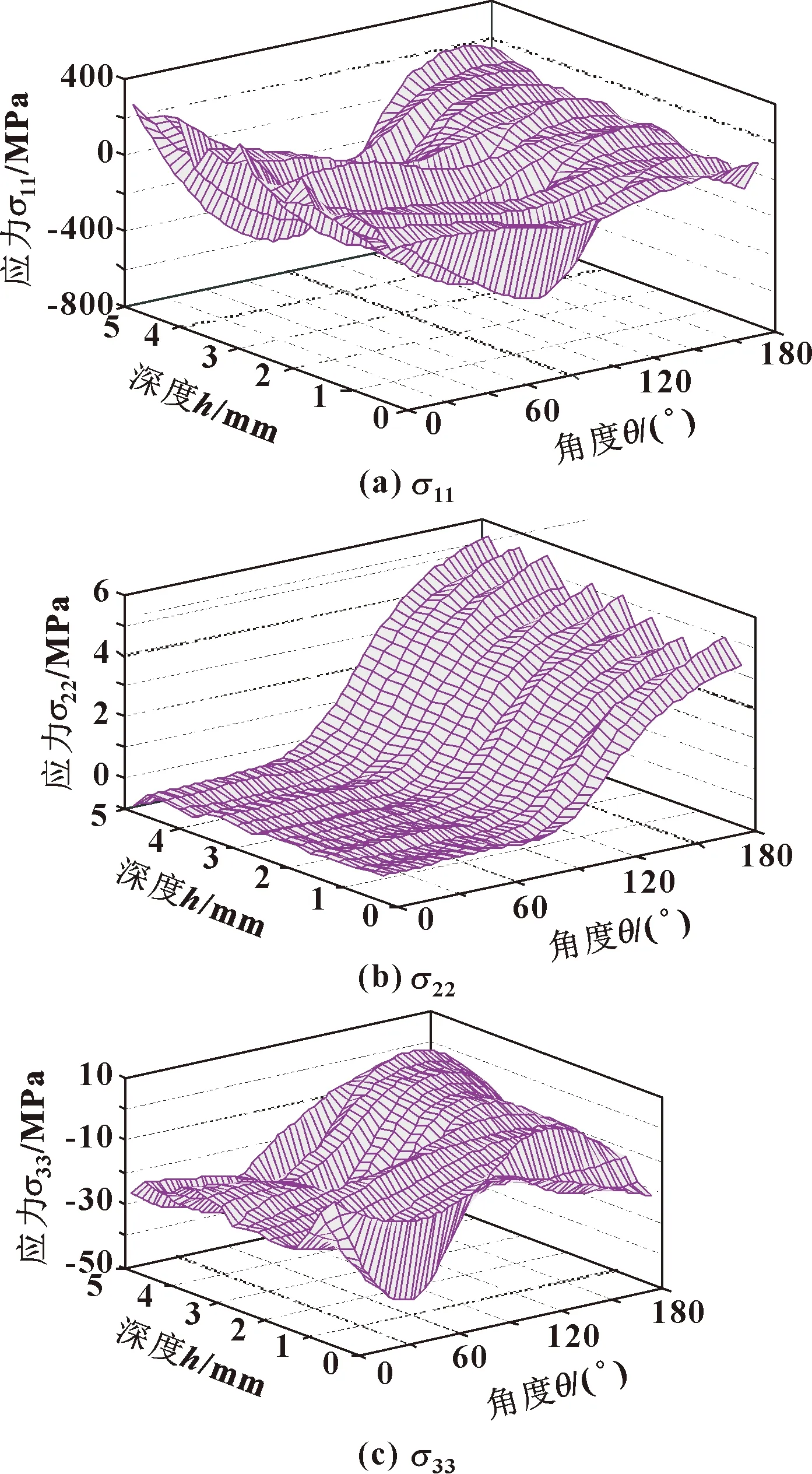
图9 90°铺层角时应力分量

σ33主要受预紧力影响，90°铺层和0°铺层的应力变化趋势及应力值变化范围趋于一致，并且都在θ为45°时达到最小。从铺层纤维方向角度关注其变化趋势，0°铺层纤维方向上的3个方向的应力变化都较平均；90°铺层纤维方向上的σ22出现了特殊的单调变化趋势；正交铺层均在加载方向上(即σ11方向)出现较大的应力变化。

4 结论

(1)建立螺栓连接复合板的渐进损伤失效有限元模型，验证了模型的有效性。

(2)随预紧力增大，螺栓连接复合板极限载荷先增大后减小，表明适当增大预紧力可有效提高螺栓连接复合板极限载荷，而过大预紧力致使复合板提前出现损伤，降低螺栓连接复合板的承载能力。随着孔隙的增加，极限载荷持续下降，这是因为增大孔隙会减小螺栓与孔的有效接触面积，对螺栓连接的压力分布和强度有一定的影响。摩擦因数对结构极限载荷的影响较小，在可控范围内，随着摩擦因数的增大，其极限承载能力提升幅度很小。

(3)当纤维铺层方向与应力分量同向时，可有效减少该方向应力分量的变化，主应力分量皆在承压区域达到其最小值。与加载方向相同方向的应力分量变化区间最大，无外力作用且应力分量方向与纤维铺层方向相同时，应力分量随圆周角变化具有单调性。