考虑O形圈初始安装变形的浮动油封接触特性*

王 娇 朱峻玉 张曰浩

(1.烟台大学机电汽车工程学院 山东烟台 264005；2.烟台大学工程实训中心 山东烟台 264005)

浮动油封作为一种常用的机械密封组件，具有良好的密封性、磨损自动补偿性、自动对中性、抗污染冲击性，广泛地运用于各种密封机械之中[1]。其可靠的密封能力主要是利用O形圈的超弹性，通过浮封环对O形圈的挤压使其产生弹性变形，使O形圈与浮封环浮封座紧密贴紧，进而阻隔外来的冲击物以及内部油液渗漏。

在O形密封圈有限元仿真方面，陈国定等[2]利用MARC软件对O形圈进行有限元仿真，研究了流体介质对轴与密封接触面剪应力与接触压力的影响。李振涛等[3]加入压缩率的影响因素，重点对von Mises应力进行分析并确定了密封材料在不同油压、不同压缩率下易于失效的位置。周志鸿等[4]就不同压缩率下O形圈易于出现裂纹的位置进行研究，通过比较接触压力与油压值的大小，分析了O形圈的密封条件。饶建华和陆兆鹏[5]考虑挡圈的影响，研究了O形圈与挡圈的接触压力、接触宽度的关系。王朝晖和何康康[6]通过非线性有限元的手段，得出O形圈接触应力与接触介质压力、压缩率的关系式。杜晓琼等[7]考虑到O形圈的安装过程，针对3种不同有限元建模思路对O形圈的接触进行比较分析。上述文献对O形圈进行了较为全面的研究，然而其接触条件，不能完全应用于浮动油封模型。

孙运友等[1]通过ANSYS建立浮动油封的有限元模型，研究了不同压缩率下O形圈对于浮封端盖的反作用力。徐卫鹏[8]考虑了材料特征与理论模型，着重分析了浮封环锥角与支反力、摩擦因数的关系。史瑞和吕晓仁[9]采用ABAQUS详细分析了不同侧向压力、摩擦因数和材料硬度下浮动油封的应力情况。浮动油封的安装要求较高[10]，而现有对于浮动油封的仿真分析忽视了O形圈安装到浮封座上后的变形，不能准确模拟实际安装中O形圈在浮动油封中的相对位置，导致在加入油压条件之后，实际状况与分析结果存在误差。

本文作者通过Ansys Workbench平台建立浮动油封的二维轴对称模型并进行非线性接触分析，以模拟浮动油封实际安装过程为基础，分析不同油压、材料硬度对浮动油封力学性能(包括浮动油封端盖支反力，浮动油封的von Mises应力、接触压力、接触摩擦力)的影响，为浮动油封在实际工况下的状态分析提供参考。

1 有限元模型

1.1 材料模型

O形圈的主要材料为橡胶，橡胶是作为一种超弹性材料，其具有各向同性，近似不可压缩性，高度变形性。对O形圈进行分析时，会涉及到3种典型的非线性问题，即材料非线性、几何非线性、接触非线性[3]。因O形圈的工况分析较为复杂，文中采用双参数模型Mooney-Rivlin定义O形圈的力学行为。选用该模型分析时，需假设：(1)O形圈的弹性模量E和泊松比μ为常数；(2)O形圈在拉压变形过程中蠕变性能一致；(3)浮封座与浮封环的材质为铸铁，硬度、刚度远超O形圈，可假设为刚体；(4)蠕变不引起O形圈的体积变化[11-13]。

关于Mooney-Rivlin的模型的计算分析，文献[6]已有详细论证。Mooney-Rivlin的本构关系公式[6，14-15]为

W=C10(I1-3)+C01(I2-3)

(1)

式中：W为单位体积的应变能函数；I1、I2为第1、第2 Green应变不变量；C01、C10为材料常数。

橡胶硬度与弹性模量的关系式为

(2)

式中：HSA为邵氏硬度。

弹性模量E与材料常数之间的关系为

E=6(C10+C01)

(3)

C01=0.25C10

(4)

(5)

其中μ取0.499。

浮封座和浮封环的材料为高铬铸铁，弹性模量为210 GPa，密度为7 850 kg/m3，泊松比为0.3。 根据上述橡胶材料的公式计算可得出如表1所示各项参数。

表1 橡胶材料参数

1.2 边界条件设置

利用Ansys Workbench对表1中3组不同硬度的O形圈进行仿真。建立浮封座与O形圈、浮封环与O形圈之间的接触，由于O形圈的硬度远小于浮封环浮封座且网格质量较好，所以O形圈为接触面，浮封环和浮封座为目标面。接触类型为摩擦接触，摩擦因数为0.2。通过网格无关性验证发现，在网格数550～1 100范围内，计算结果误差始终保持在5%以内，故采用自由网格划分浮动油封模型，网格单元数为847个，网格节点数为2 744个，有限元模型如图1所示。

图1 浮动油封的有限元模型

首先模拟O形圈的装配过程，在浮封座底端和右侧施加固定约束，使其在X、Y方向上不发生移动，在浮封环左侧施加位移约束，在浮封环上端施加位移约束，使其沿Y轴负方向位移。O形圈保持自由运动，当其达到安装位置(两侧浮封环端面到浮封座端面距离为2～4 mm)时，在O形圈下边缘施加垂直向上均匀分布的压力载荷模拟油压。分析过程分为20个载荷步，采用缓慢施加载荷的形式加载，并将大变型打开，进行求解计算[11]。

2 结果及分析

2.1 考虑或不考虑安装过程时浮动油封接触对比

安装间隙为2 mm时，考虑或不考虑安装过程时O形圈相对位置如图2所示。可知，考虑安装过程的情况下，O形圈并不是在浮动油封中相对居中的位置，而是在中部偏上位置；考虑安装过程时O形圈最大von Mises应力相对于未考虑安装过程时高近9.5%，且未考虑安装过程的浮封环端面支反力为1 431 N，与实验值1 890 N的误差为24%左右，误差较大，故采用考虑安装过程的方法分析浮动油封更为准确。

2.2 油压对O形橡胶圈von Mises应力的影响

图3示出了安装间隙为3 mm的O形圈在不同油压下的最大von Mises应力，图4示出了不同油压、不同装配间隙条件下的最大von Mises应力分布。

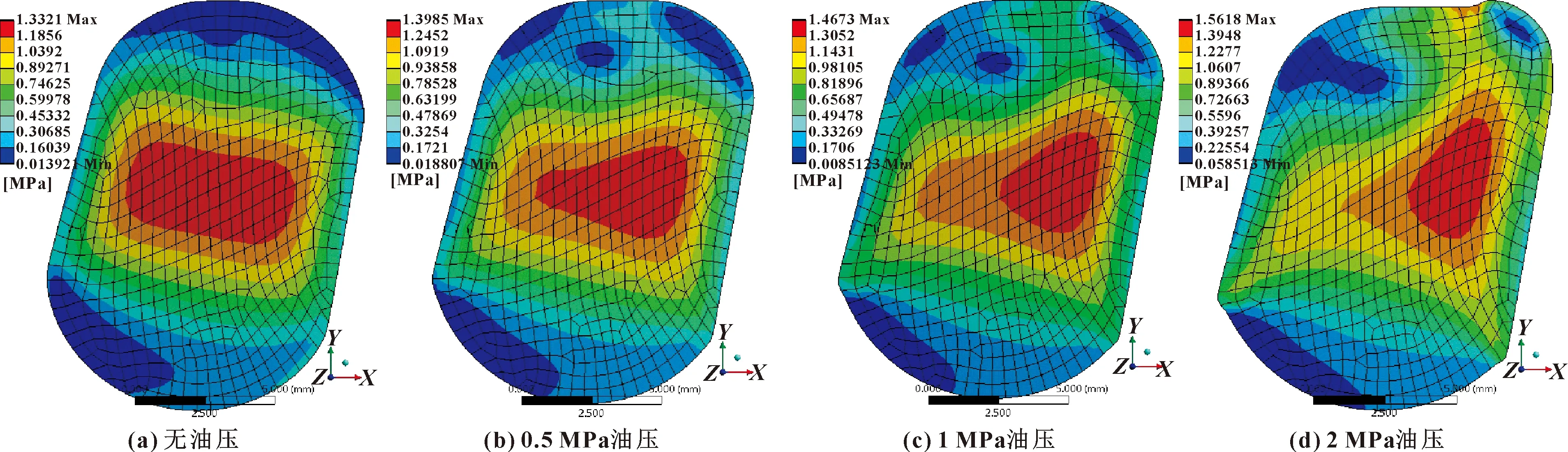
图3 安装间隙为3 mm的O形圈在不同油压下的最大von Mises应力

由图3(a)可知，无油压时O形圈的最大von Mises应力主要集中在O形圈的中间位置，其形状呈哑铃状[9]。由图4可知，安装间隙一定时，随着油压的升高，O形圈的最大应力逐渐增大，且其峰值区域位置逐渐向浮封座与浮封环的间隙方向上靠拢(见图3(b)—(d))，说明油压的增大使得O形圈的应力更加集中，会加速O形圈松弛，引起刚度的降低，易产生裂纹[16]。

图4 不同油压、不同装配间隙条件下的最大von Mises应力

2.3 安装间隙对O形圈von Mises应力、接触摩擦力的影响

图5示出了1 MPa油压下O形圈在不同安装间隙下的最大von Mises应力，图6示出了不同油压、不同装配间隙条件下的最大接触摩擦力。

由图5可知，油压一定时，安装间隙越大，O形圈所承受的最大von Mises应力越小；其应力的集中区域随着安装间隙的减少，逐渐向浮封座与浮封环的间隙方向上移动。这表明在安装过程中，安装间隙小的O形圈的应力更加集中且应力更大，易于造成应力松弛，不利于其内部弹性势能释放，降低了浮动油封轴向补偿功能，进而降低了O形圈的生命周期[17]。但安装间隙较大则会造成密封效果的降低。

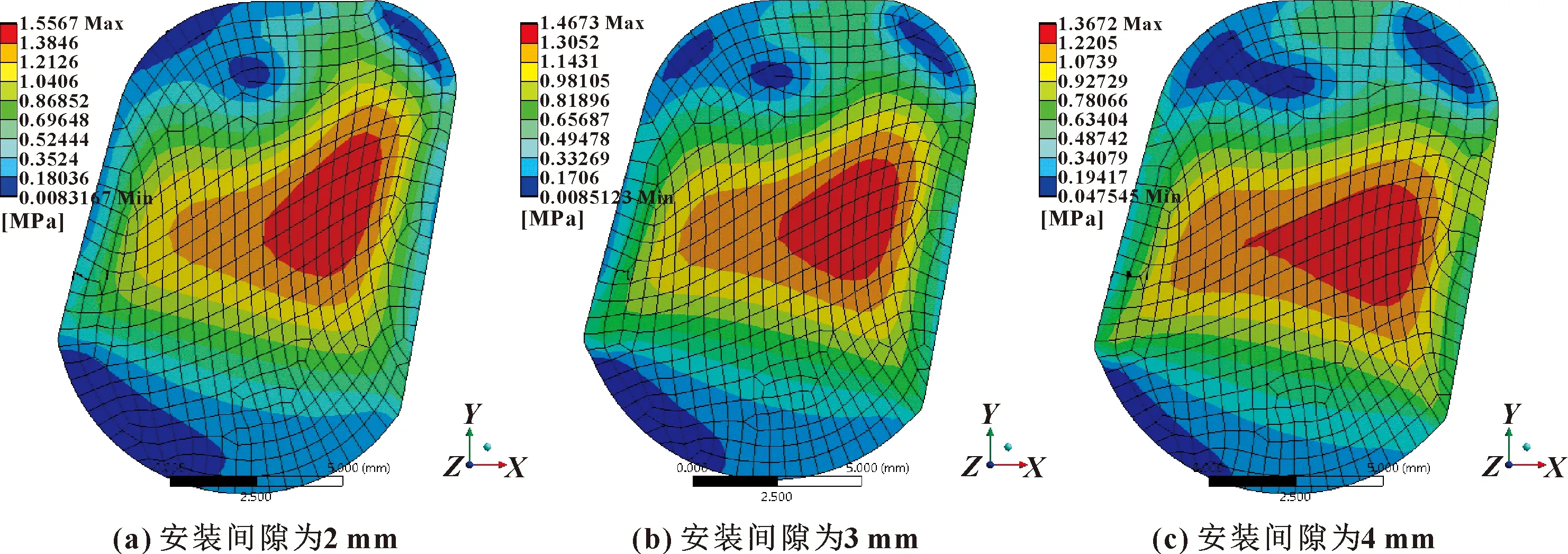
图5 1 MPa油压下O形圈在不同安装间隙下的最大von Mises应力

由图6可知，在无油压时，间隙越小，初始最大接触摩擦力越大；在2 mm的安装间隙下，最大接触摩擦力随油压先减少后增加；在3 mm的安装间隙下，最大接触摩擦力随油压先缓慢增加后迅速增加；在4 mm的安装间隙下，最大接触摩擦力先迅速增加后增长放缓。这是由于在安装时，O形圈的运动趋势向下，随着由油压的施加，O形圈的运动趋势向上，造成初始接触摩擦力与2 MPa时接触摩擦力方向不同，产生抵消，最终随着油压的增大会维持间隙越小，最大接触摩擦力越大这一现象。

图6 不同油压、不同装配间隙条件下的最大接触摩擦力

2.4 油压对O形橡胶圈接触压力的影响

图7示出了安装间隙为3 mm时不同油压下的接触压力分布。可知，安装间隙一定时，油压值越大，O形圈在油压的作用下越容易被挤入浮封座与浮封环的间隙。在一定范围内接触压力随着油压值呈近似线性增长,其压力的峰值区域的接触长度也随之增大。由于最大接触压力始终大于油压值，说明在不同油压工况下，O形圈均能保持良好的自密封能力[17]。

图7 安装间隙为3 mm时不同油压下接触压力分布

2.5 油压对O形橡胶圈接触摩擦力的影响

图8示出了安装间隙为4 mm时不同油压下接触摩擦力分布。由图6、图8可知，达到安装位置时，接触摩擦力的最大值出现在浮封座与O形圈的接触面，最小值位于浮封环接触面；施加油压使得接触摩擦力的峰值区域由浮封座向浮封环转移；在一定范围内接触压力随着油压的增大而增大，其峰值区域随着油压的增大而增多，且接触摩擦力最大值逐渐向O形圈上侧与浮封环接触区域移动。这表明在高油压的情况下，摩擦力较大且集中于一个区域中，会加剧O形圈的磨损，产生漏油，降低浮动油封的使用寿命[18]。

图8 安装间隙为4 mm时不同油压下接触摩擦力分布

2.6 油压对浮封环端面支反力的影响

图9示出了安装间隙为3 mm时不同油压下接触支反力方向，图10示出了不同油压、不同装配间隙条件下的最大支反力分布。可知，安装间隙一定时，施加油压越大浮封环对O形圈产生的支反力就越大；油压一定，间隙越大，支反力越小；浮封环支反力的方向随着油压的增加逐渐向y轴方向移动，高油压y方向的作用力大于x方向，且增速更快，使得浮封环更容易发生轴向移动，不利于维持浮封环端面与轴的同轴度，易于失效。

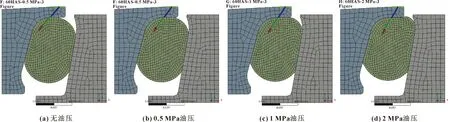
图9 安装间隙为3 mm时不同油压下接触支反力方向

图10 不同油压、不同装配间隙条件下最大支反力分布

2.7 硬度对O形橡胶圈接触摩擦力的影响

图11示出了不同油压、不同硬度下的最大von Mises应力、最大接触压力、最大接触摩擦力分布。可知，O形圈的硬度越高，O形圈所受的最大von Mises应力、最大接触摩擦力、最大接触压力越高，且在不同油压作用下这一规律依然存在。

图11 不同油压、不同硬度下最大von Mises应力、最大接触压力、最大接触摩擦力分布

2.8 模型验证

文中现阶段只实验测量初始未加压时不同安装间隙浮封环端盖支反力情况,加压实验尚需进一步实验。图12所示为浮封环端盖支反力仿真结果与实验结果对比。在安装间隙范围内，在间隙值为2.6 mm时，仿真与实验结果误差最大，约为5.5%，其余间隙值时两者误差均低于5%，验证了仿真结果具有较高的可靠性。

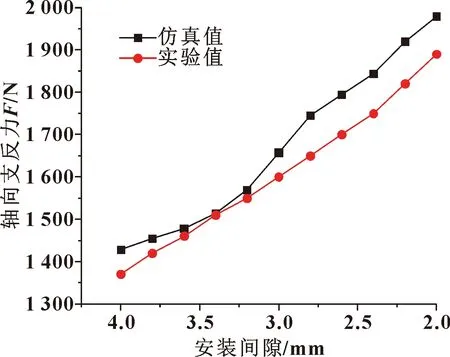
图12 浮封环端盖支反力仿真结果与实验值对比

3 结论

(1)考虑安装过程的情况下，O形圈并不是在浮动油封中相对居中的位置，而是在中部偏上位置；考虑安装过程时O形圈最大von Mises应力相对于未考虑安装过程时高近9.5%，因此采用考虑安装过程的方法分析浮动油封更为准确。

(2)在安装间隙和O形圈硬度一定时，O形圈的应力随油压的升高而增大，O形圈部分被挤入到浮封座与浮封环的间隙，最大von Mises应力也从中间区域向间隙侧移动，最大应力区域变小变窄，应力更加集中。O形圈的最大接触摩擦力随油压升高而逐渐增加，使得接触摩擦力的峰值区域由浮封座转移向浮封环。浮封环端面支反力随油压升高而升高且y方向作用力的增速远超x方向作用力的增速，这就使得浮封环易被顶出，影响浮封环与轴的同轴度。表明在高油压下会加剧O形密封圈磨损，同时加大产生裂纹失效的风险。

(3)在恒定油压的情况下，应力随安装间隙的减小而增大，应力随硬度的增加而增大。由于安装间隙较小或O形圈硬度较低，会造成应力松弛，阻碍了O形密封圈内部弹性势能释放，降低浮动油封轴向补偿功能，且易于漏油；而较大的安装间隙时O形圈会更易于被挤出，同时间隙过大易造成泄漏增大；较高硬度的O形圈，则会加大磨损，降低使用寿命，因此需要根据实际工况选择合适的安装间隙与硬度。

(4)浮动油封在2 MPa油压范围内，最大接触压力随油压增大而增大，峰值区域的接触长度也不断增加，增强了密封效果，通过接触压力与油压值的比较验证了浮动油封的自密封能力。