关注“平均变化率” 速解函数应用问题

刘 瑛

(甘肃省陇南礼县第一中学 742299)

随着核心素养的提出，与图象有关的函数应用问题是近年高考数学的热点，这类问题往往考查学生对函数自变量和因变量变化情况的分析能力，在解题中借助“平均变化率”达到简洁求解之目的，有利于培养学生数形结合的能力以及数学的应用意识.

1 理论阐述

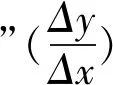
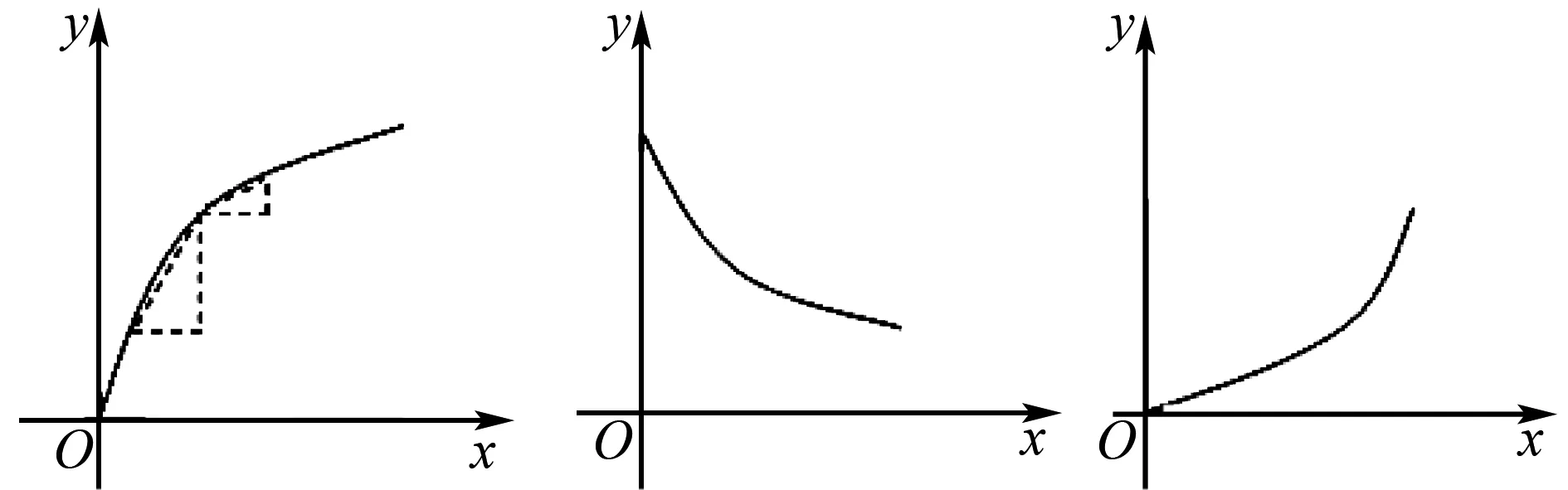
图1 图2 图3

类似分析可得，图2对应“平均变化率”越来越小；图3、图4对应“平均变化率”越来越大；图5、图6对应“平均变化率”不变.

图4 图5 图6

2 应用举例

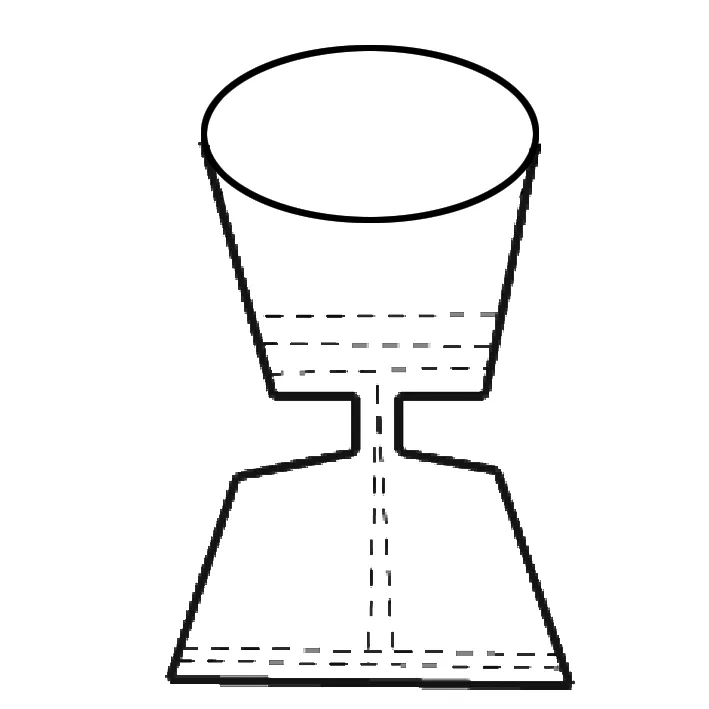
图7

“平均变化率”的特征比较明显，学生易于掌握，教师引导学生明确上述图形及其相关特点，在具体问题中应该结合“平均变化率”的实际特点，将数学问题转化为“平均变化率”问题，则求解此类相关问题即可达“事半功倍”之效.

2.1 具体求解，不涉及分类讨论

例1 如图7所示，现有一个计时漏斗，开始时盛满沙子，沙子从上部均匀漏下，经过5分钟漏完，h(厘米)是该沙漏中沙面下降的高度，则h与下漏时间t(分钟)的函数关系式用图象表示应该是( ).

图8

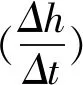
评注结合所给实物图形，理清整个实际变化过程是准确求解的切入点；其次，要注意学会观察、分析给定的函数图象.

牛刀小试1 某学生离家去学校，为了锻炼身体，一开始跑步前进，跑累了再走余下的路程，现用纵轴表示离学校的距离，横轴表示出发后的时间，则下列四个图形中较符合该学生的走法的是( ).

图9

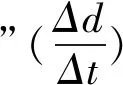
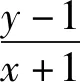
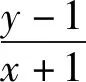
化简,得kx-y+k+1=0.

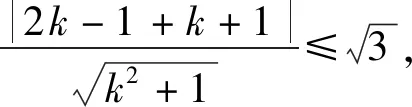
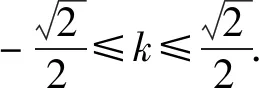
2.2 具体求解，涉及分类讨论

例2如图10所示，直角梯形ABCO中，AB∥OC，BC⊥OC,AB=1,OC=BC=2，直线l：x=t截此梯形所得位于l左方图形的面积为S，则函数S=f(t)的图象大致为( ) .

图10

图11

综上，易知选项C正确.

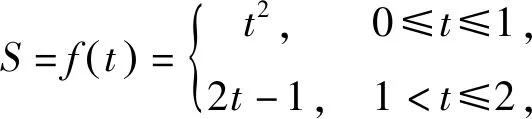
图12

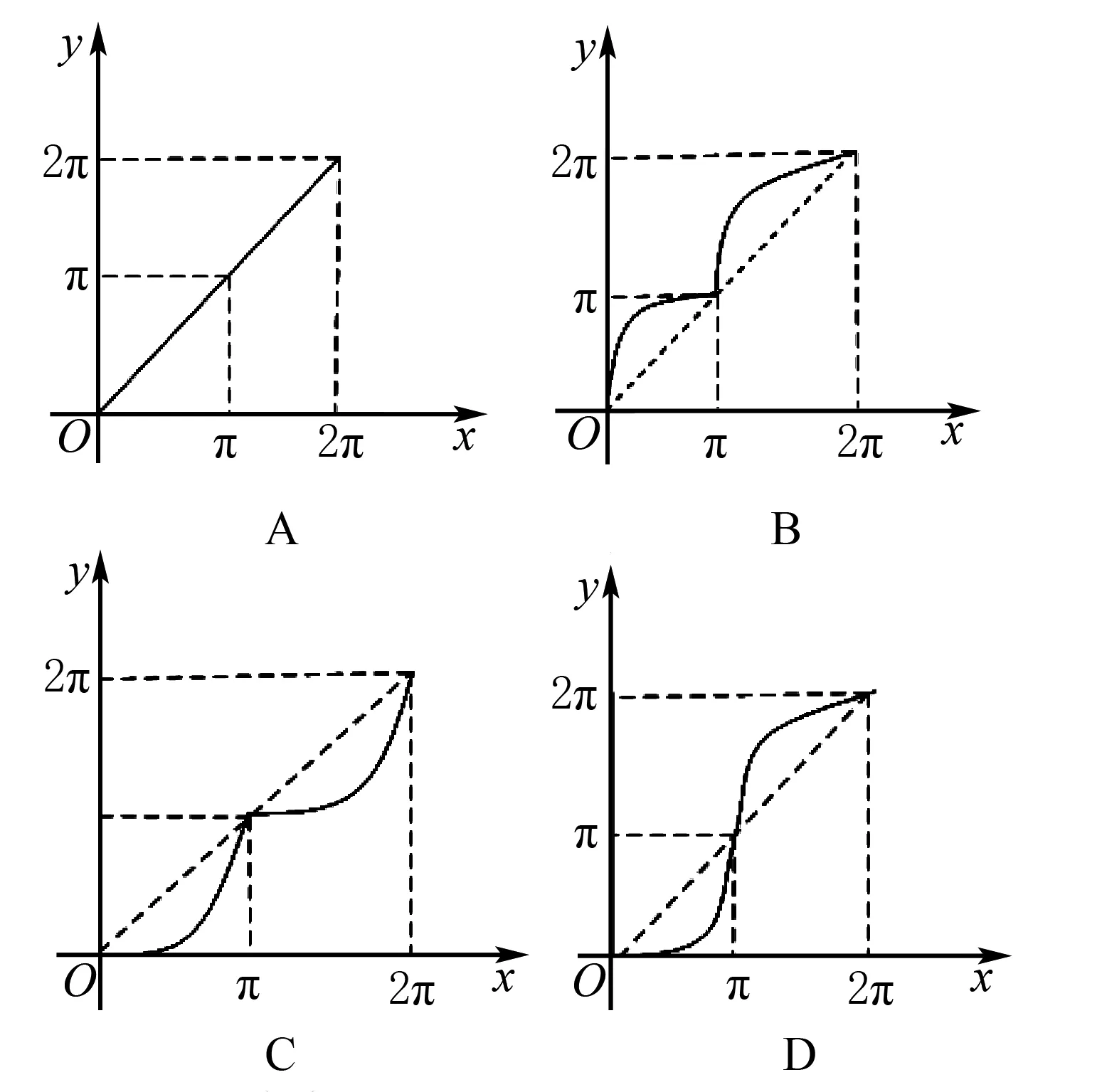
图13

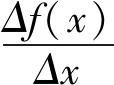
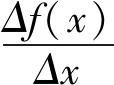
综上，易知选项D正确.

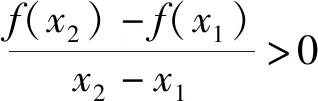
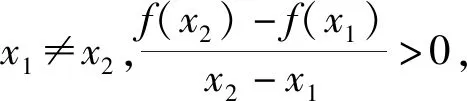
因此，使得不等式f(2a-3)

总之，从数形结合的角度，准确理解、掌握描述两个变量之间的变化关系的量——“平均变化率”，可帮助我们顺利求解以图形为载体，考查有关函数的实际应用问题，进而增强学生的识图、用图能力，有利于较好地培养学生的直观想象能力以及推理、判断能力.