巧思维切入 妙技巧类比
——一道离心率的求解
2022-11-03廖昕
廖 昕
(甘肃省兰州市第三中学 730000)
涉及圆锥曲线离心率的求值或取值范围问题,变化多端,破解时往往思维多样、策略多变、技巧多样,解决问题时或一种策略独领风骚,或多种策略齐心协力,或另辟蹊径,合理转化,巧妙破解.
1 问题呈现
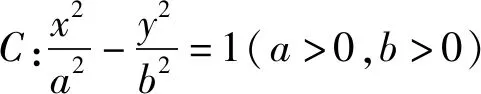
此题以双曲线为问题背景,通过双曲线的两个焦点与一个顶点,以及双曲线上的一个点,组成一个复合的三角形,利用相关内角之间的相等、倍数关系等合理构建,进而确定双曲线的离心率的值.
2 问题破解
解法1(三角函数定义+余弦定理法)
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
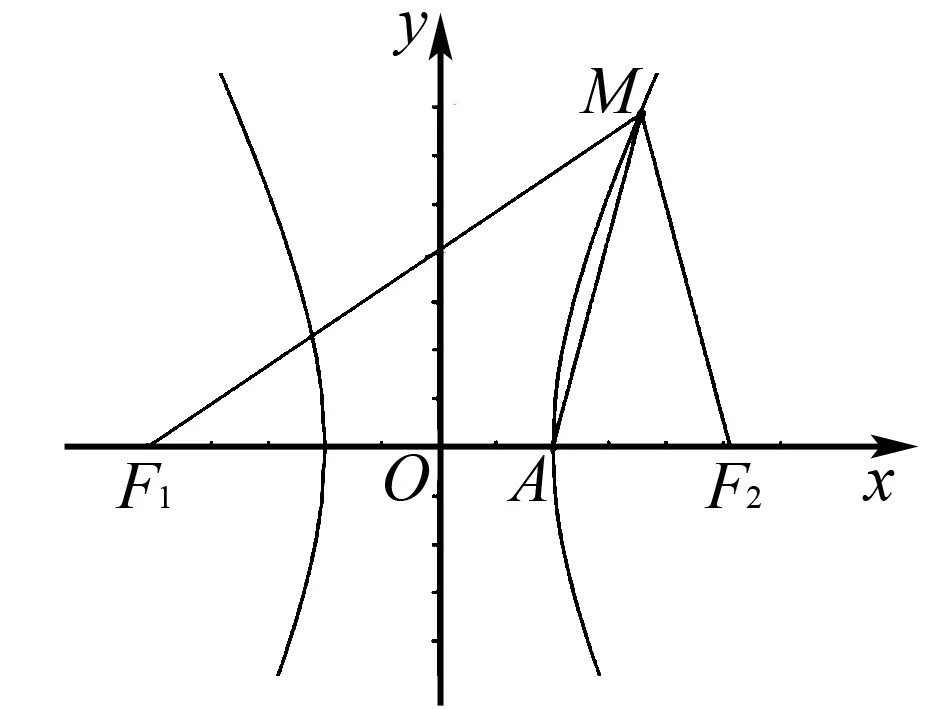
图1
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.

利用余弦定理有
由cos∠MAF2+cos∠MAF1=0,可得
整理,得c2-ac-4a2=0.
即e2-e-4=0.

解法2 (余弦定理法)
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.
利用余弦定理有

整理得(c-a)(c2-ac-4a2)=0.
即c2-ac-4a2=0.下同解法1.
解法3(相似三角形法)
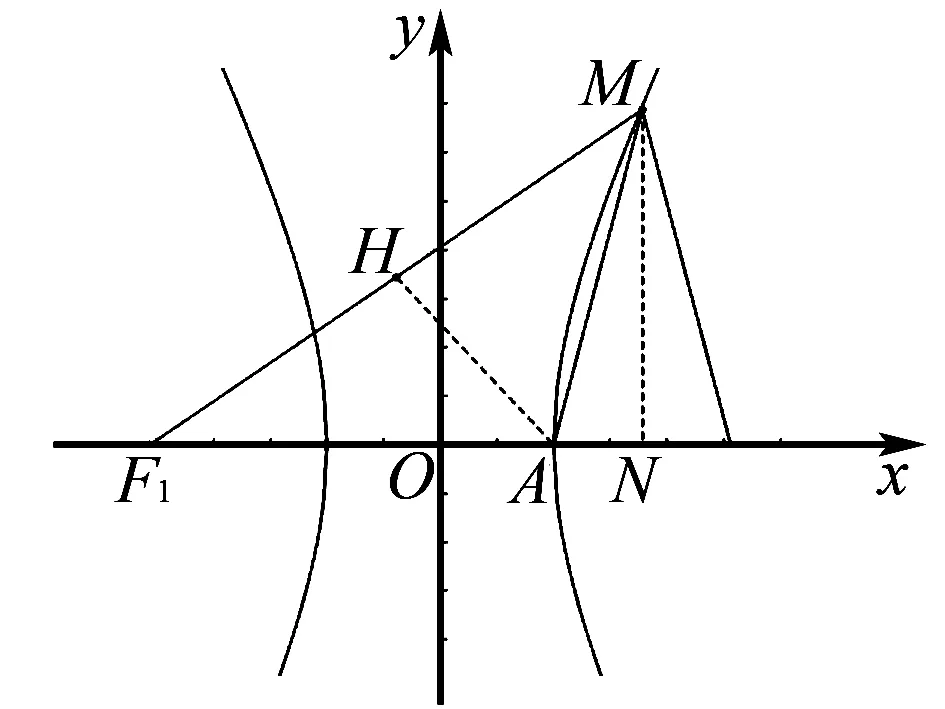
图2
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.
如图2,过点M作MN⊥x轴,垂足为点N,过点A作AH⊥MF1,垂足为点H,则有
易得Rt△MF1N∽Rt△AF1H.

整理,得c2-ac-4a2=0.下同解法1.
解法4(勾股定理法)
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.
过点M作MN⊥x轴,垂足为点N,过点A作AH⊥MF1,垂足为点H,则有
利用勾股定理,在Rt△AMN中,可得
又在Rt△F1MN中,可得
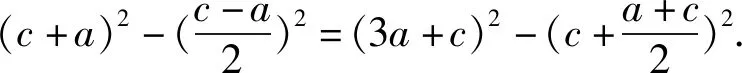
整理,得c2-ac-4a2=0.下同解法1.
解法5(二倍角公式法)
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.
过点M作MN⊥x轴,垂足为点N,则有
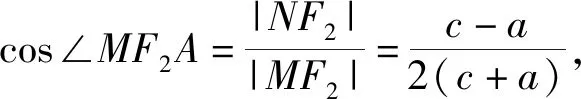
而∠MF2A=2∠MF1A,结合二倍角公式可得
整理,得c2-ac-4a2=0.下同解法1.
解法6(二倍角三角形性质法)
因为∠MF2A=∠MAF2=2∠MF1A,
则有|AM|=|MF2|=|AF1|=c+a.
结合双曲线的定义,可得
|MF1|=2a+|MF2|=3a+c.
在△MF1F2中,∠MF2A=2∠MF1A,
结合二倍角三角形性质,可得
(3a+c)2=(c+a)(c+a+2c).
整理,得c2-ac-4a2=0.下同解法1.
3 变式拓展
探究1 保留题目创新情境,改变圆锥曲线的类型,将原来的双曲线问题类比到椭圆问题,保留相关条件以及角之间的关系,同样可以确定椭圆的离心率问题,得到以下相应的变式问题.
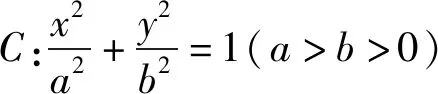
解析因为∠MF2A=∠MAF2=2∠MF1A,则有|AM|=|MF2|=|F1F2|=2c.
结合椭圆的定义,可得
|MF1|=2a-|MF2|=2a-2c.
在△MF1A中,∠MAF2=2∠MF1A,
结合二倍角三角形性质,可得
(2a-2c)2=2c(2c+a+c).
整理,得c2+5ac-2a2=0.
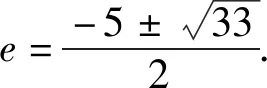

探究2保留题目的创新背景,改变题目部分条件,以等腰三角形以及对应的线段长度等为背景来创设,进而确定相应双曲线的离心率.
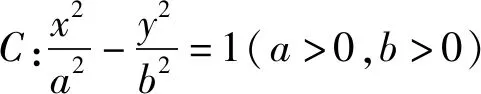
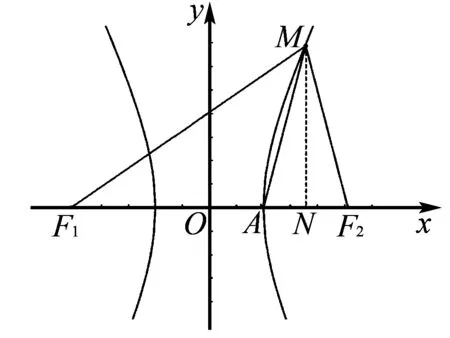
图3
解析结合双曲线的定义,可得
|MF1|=2a+|MF2|=5a,解得|MF2|=3a.
如图3,取AF2的中点N,由△F2MA是以∠AMF2为顶角的等腰三角形,可知MN⊥F1F2.
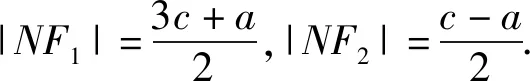
利用勾股定理,可得
整理,得c2+ca-8a2=0.
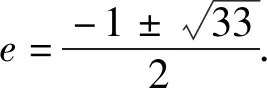
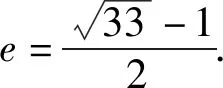
4 解后反思
4.1 思维发散,方法归纳
破解以双曲线为载体的圆锥曲线问题,利用圆锥曲线的定义确定相应的线段长度,利用条件中角之间的关系,可以考虑从解三角形思维、平面几何思维、三角函数思维、特殊三角形思维、解析几何思维以及圆锥曲线的定义思维等来切入,结合平面几何、余弦定理、三角函数以及距离公式等知识,归纳相应的方法来分析,达到解决问题的目的.
4.2 探究拓展,能力提升
涉及圆锥曲线的问题,可以在一定条件下加以合理类比,进而挖掘、探究,得到与之相关的其他问题,拓展思维,从而全面提升思维能力、解题能力,提升数学品质,提高数学能力,培养核心素养.
