一道双变元代数式最值的探究

王 健

(安徽省滁州中学 239000)

涉及双变元(或多变元)代数式的最值或取值范围问题是高考、自主招生以及各类数学竞赛中的热点之一．此类问题的破解方法与切入点多种多样，往往能合理交汇数学知识，融合数学思想，拓展思维方法，提升数学能力，是培养考生的数学核心素养的一大主阵地，备受各方关注．

1 问题呈现

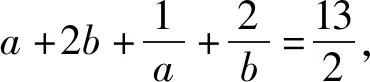
2 问题剖析

此题以双变元的代数式的值为条件，进而求解其中涉及一次分式的关系式的最大值与最小值，参数不具有对称性或轮换性，没有特殊的规律．

结合题目条件与代数关系式的特征，可以通过换元思维(单变量换元或双变量换元)，利用解二次不等式来达到目的；可以通过配凑思维，利用基本不等式来达到目的；可以借助不等式的性质以及不等式的求解，借助不等式性质达到目的；还可以通过重要不等式，利用权方和不等式来达到目的等．

3 问题解决

解法1(换元法1)结合基本不等式，可得

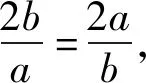
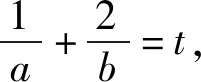
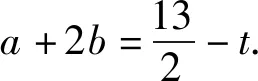
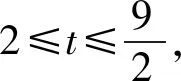
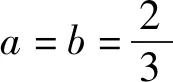
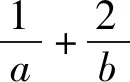
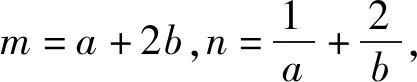
由柯西不等式，可得

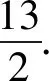
解后反思根据题目条件中代数式的结构特征，通过巧妙换元处理，进行整体化思维，利用条件加以代换，转化为含有一个参数的函数、方程或不等式问题，从而更加有效地利用函数性质、方程的解或不等式的应用等来解决代数式的最值问题．

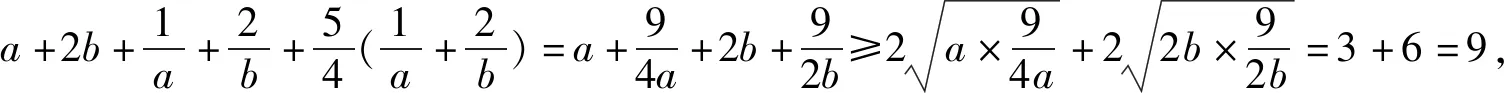
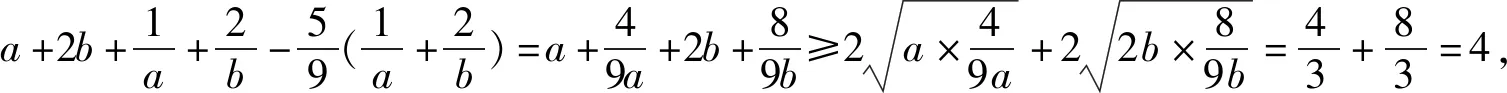
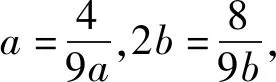
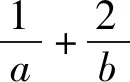
解后反思根据题目条件中代数式的结构特征，进行合理的配凑处理，使得对应的代数关系式更加吻合重要不等式的特征，为进一步确定代数式的最值提供条件．配凑法处理问题时，技巧性强，具有一定的“设计”性与目的性，对数学运算、逻辑推理以及数学思想方法的要求非常高．

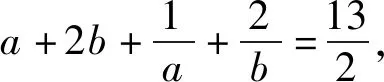
利用基本不等式，可得

3.1 烟农文化水平低、种植分散管理困难 该研究中烟农以中青年男性为主，整体文化程度低，大部分人只有初中及以下学历。烟农文化素养低，虽然参加过一些相关培训，但在实际操作中，并没有严格遵守规定，缺乏用药安全意识，不能做到科学用药。全州种烟农户以5年以上的小面积烟农为主，仅有岑巩县地区3.3 hm2以上大户比较多，因户均面积小、烤烟种植较分散、管理难度大，难以有效监督农药使用情况，容易造成农药残留。

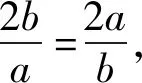
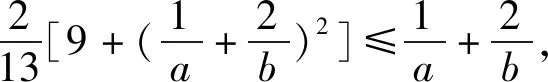
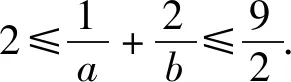
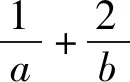
解后反思根据题目条件中代数式的结构特征，对所求的代数关系式进行整体化思维，综合利用代数关系式的恒等变形与转化，以及基本不等式的应用、二次不等式的求解等，综合不等式的性质等来巧妙处理，实现问题的巧妙转化与应用．

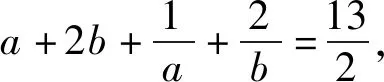
化简，得2(a+2b)2-13(a+2b)+18≤0.

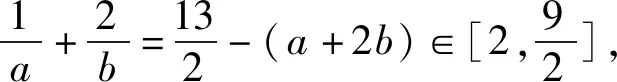
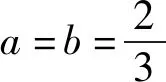
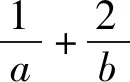
解后反思根据题目条件中代数式的结构特征，结合代数式的合理化归与转化，借助一些常见的重要不等式(柯西不等式、权方和不等式、排序不等式等)来分析与处理．

4 变式拓展

探究1保留原来题目的条件，将求解相关代数式的“最大值与最小值之和”问题变为求解“最大值”或“最小值”问题．

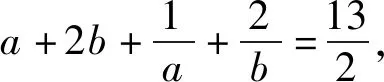
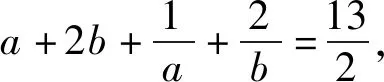
解后反思根据以上变式问题的创设，只求出相应代数关系式的最大值或最小值，目标更加直接，难度也有所降低，比较吻合中等学生的能力范围．

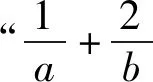
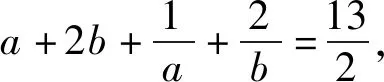
解析结合基本不等式，可得

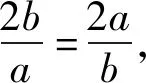
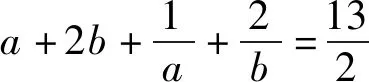
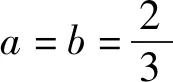
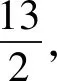
解后反思这里只是以上变式问题的一种解析方法，还可以参照原问题的不同解析思维与方法，同样可以用来解决该变式问题，这里不多加以叙述．

5 教学启示

5.1 通技通法，技巧策略

破解双变元代数式的最值问题，关键是利用题目条件，通过合理配凑与巧妙转化，借助基本不等式以及柯西不等式、权方和不等式等一些重要不等式来确定最值问题．而其他的技巧方法，如换元、配凑、不等式求解等方法的应用，是在整体思维下的一点灵活变通与创新．

5.2 思维视角，能力提升

具体解决涉及双变元代数式的最值(最大值或最小值)或取值范围问题，破解思维各异，但一些基本的破解思维和常见方法值得我们系统掌握，并在此基础上举一反三、融会贯通、深化思维、巧妙转化、合理应用，学会变式拓展，发散数学思维，养成良好的学习习惯与思维方式，提升数学思维品质，提高数学能力，培养数学学科的核心素养．