七种方法求解直线方程

卢会玉

(甘肃省嘉峪关市第一中学 735100)

高考对直线方程的考查也是比较常见，但是一般都是选择或者填空题.有时用相关的平面几何的知识解决问题是非常快捷的，有时用适合题目特点的一些方法也是比较合适.本文对一道涉及角平分线的题进行了深入的分析和探究，用七种方法揭秘这种类型问题的解法.

1 试题呈现

题目已知△ABC的三个顶点坐标分别为A(2,3),B(-2,0),C(2,0),则∠A的平分线所在直线l的方程为____.

2 试题解析

解法1(利用角平分线的性质求解)易知直线AB的方程为3x-4y+6=0，直线AC的方程为x=2.

设M(x,y) 是l上任意一点，则由点M(x,y)到两直线AB,AC的距离相等，得

化简,得2x-y-1=0 ，或x+2y-8=0(易知斜率为负的舍去).

故所求直线l:2x-y-1=0.

解法2(利用角平分线的性质及线性规划知识求解)易知直线AB的方程为3x-4y+6=0，直线AC的方程为x=2.

化简,得2x-y-1=0，即为所求.

图1

则容易求得l:2x-y-1=0.

解法4(利用平面几何知识求解)依题意可知，直线l必过△ABC的内切圆的圆心，设内切圆的圆心为P，半径为r(如图2).

图2

又由|AB|=5,|BC|=4,|AC|=3可知，△ABC为直角三角形.

所以P(1,1).

由直线l过P(1,1)和A(2,3)，

容易求得l:2x-y-1=0.

解法5(利用等面积法求解)依题意可知，直线l必过Rt△ABC的内切圆的圆心，设内切圆的圆心为P，半径为r.

由直角三角形可知

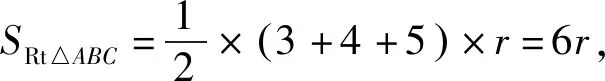
所以6r=6.即r=1.则P(1,1).

由直线l过P(1,1)和A(2,3)，

容易求得l:2x-y-1=0.

解法6(利用等面积法求解)设l与x轴的交点为D(x0,0)，则点D到直线AB的距离d=|DC|=2-x0(如图3).

图3

又|BD|=x0+2，则

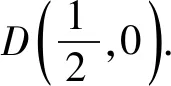
则容易求得l:2x-y-1=0.

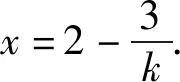
则tan∠BAD=tan(∠ADC-∠ABD)

故所求直线l:2x-y-1=0.

以上七种解法，有的灵活运用了角平分线的定义、点到直线的距离公式、线性规划等知识；有的巧用了三角形内角平分线和圆的切线性质，利用了内切圆半径r与Rt△ABC的三边关系；有的灵活运用了等面积法，从而快捷地求得内心的坐标及直线l的方程；有的利用了三角函数知识解决了问题.应该说不同的方法打开不同的思维通道，能给人很多启发.