研究离心率的求法——以一道质量检测题为例

徐 健

(新疆教育科学研究院 830049)

2022年3月23日下午，乌鲁木齐地区全体高三学生和部分高中数学老师参加了本地高度重视的高三第二次质量检测考试，题目较以往有明显的变化：新颖但偏易！但是第11题大家一致反映不好做，花了很多时间却无果而终，甚至影响了后续答题，这种反应老师中也存在.因此，我第一时间展开了研究，先分享于此，以飨读者.

1 题目呈现

2 总体把握

要求双曲线的离心率，本质就是寻求其参数a，c的关系，进而要寻找建立关系的条件.显然点P，Q在双曲线的渐近线上就是突破口，那么这两点的坐标必须被双曲线的参数a，b，c表达，所以问题归结为探究点P，Q的坐标.由几何位置关系知，点P制约着点Q，因此突破点P的坐标是关键，我们尝试着用a，b，c来表达.

3 解法探究

策略1 估算速解.

解法1 如图1，记坐标原点为O，显然OP是Rt△PF1F2斜边上的中线，于是|OP|=c.

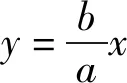
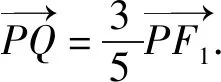
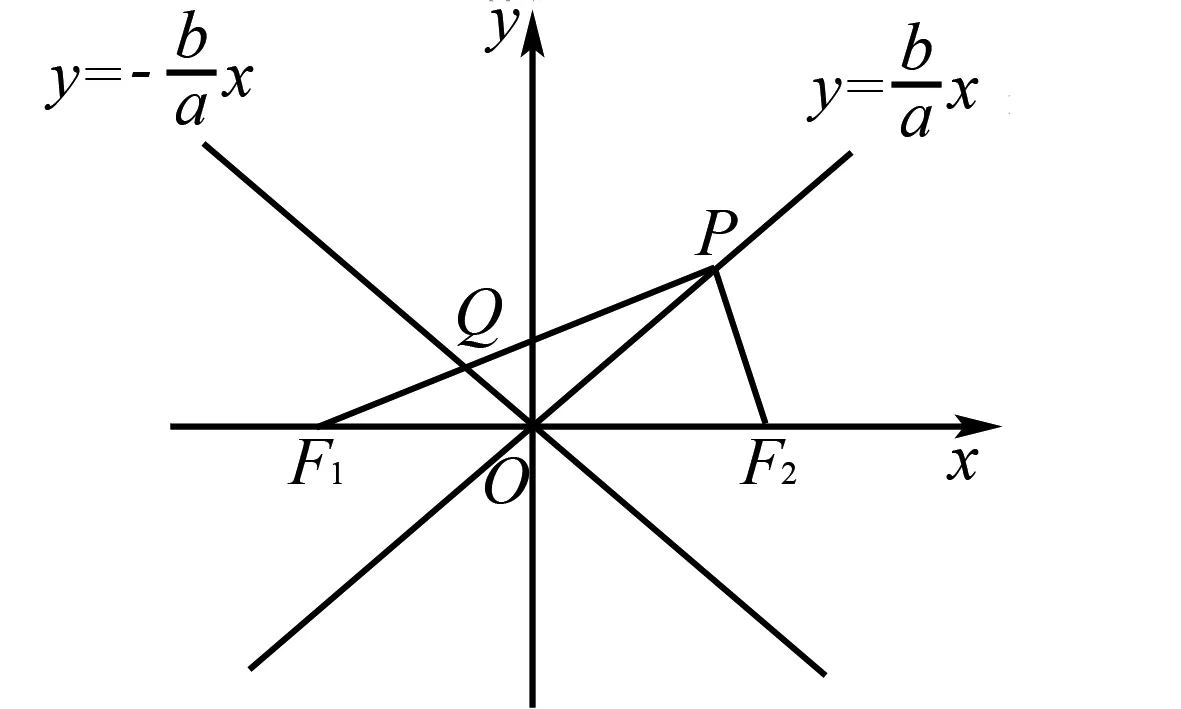
图1

设Q(m,n)，则

(*)

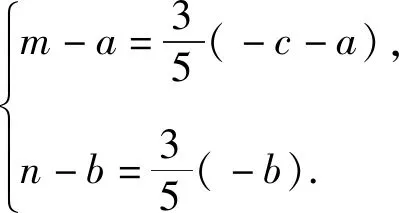
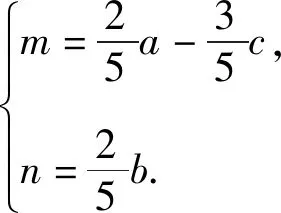
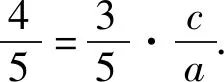
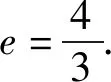
故选B.

评注作为考试，又快又准答题是非常重要的.估算猜想可以实现速解.猜想当然需要解题经验和正确的理论支持.本解法就是依据曲线与方程的关系和参数的数量关系c2=a2+b2合理推理后猜想而得.

策略2 利用直线和圆的方程求交点.

解法2 因为PF1⊥PF2，所以点P的轨迹方程为x2+y2=c2(除去点F1，F2).

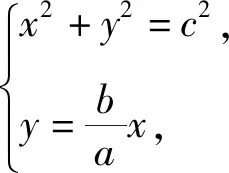
整理,得(a2+b2)x2=a2c2.

因为a2+b2=c2，

所以c2x2=a2c2.

解得x=a.

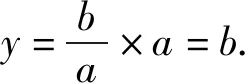
因此点P的坐标P(a,b).

以下同解法1.

策略3 利用向量垂直建立方程.

解法3 因为PF1⊥PF2，

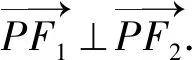
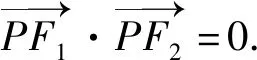
设P(s,t)，

则(-c-s,-t)·(c-s,-t)=0.

整理，得s2+t2=c2.

①

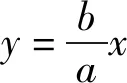
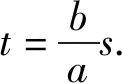
②

有①②解得P(a,b).

以下同解法1.

策略4 依托斜率关系式建立方程.

解法4 因为PF1⊥PF2，

所以kPF1·kPF2=-1.

设P(u,v)，

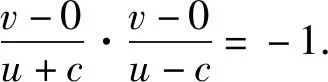
整理,得u2+v2=c2.

③

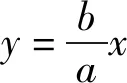
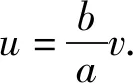
由③④解得P(a,b).

以下同解法1.

策略5依托两直线方程求点Q的坐标.

解法5由前文知点P(a,b)，又F1(-c,0)，所以F1(-c,0).

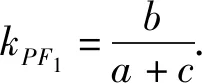
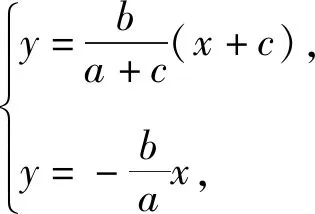
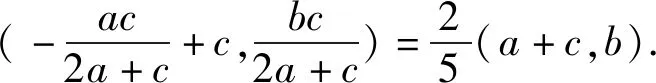
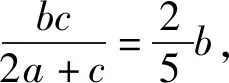
得4a=3c.

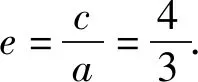
故选B.

评注解法2，3，4，5均在交点上做文章，只是曲线(直线)方程产生的渠道不同而已，殊途同归.可以根据自己的喜好进行选择，运算量差距不大.多角度思考，有助于提高学生的应试能力，拓广思维.而考生思维受阻的原因是引入变量太多，将点P，Q的横纵坐标均看作相互独立的4个变量，未准确把握它们之间的数量关系.

策略6 依托三角函数关系式建立方程.

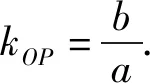
由同角三角函数的基本关系,得

由直角三角形中的三角函数,得

因此点P的坐标P(a,b).

以下同解法1.

评注解析几何中恰当引入三角函数往往可以减少变量，降低运算量.本题的相关点不在双曲线上，不易引入三角函数，需要综合考虑，从直线倾斜角的角度引入角，然后才有三角运算，解题过程十分简洁.

策略7 几何法，构造相似形直接得解.

解法7如图2，设点P关于y轴的对称点为P′，结合前文得P′(-a,b).

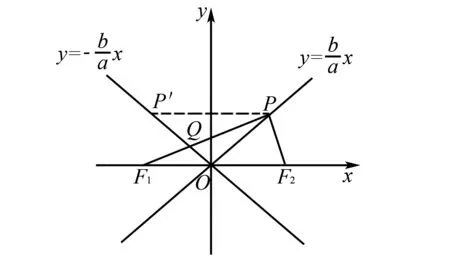
图2

同时，PP′∥OF1.

所以△QPP′∽△QOF1.

于是|PQ|∶|QF1|=|PP′|∶|OF1|.

因为|PQ|∶|QF1|=3∶2，

所以|PP′|∶|OF1|=2a∶c=3∶2.

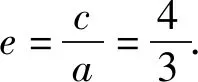
评注解析几何的本质是几何，能够将解析几何问题的数量关系转化为几何位置关系，通常会大大降低运算量，使解题显得简洁明了.当然，这种转化还是很不容易的，纵观以上解法，本解法最为巧妙便捷.

4 追踪溯源

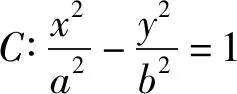
参考答案C.

参考答案C.

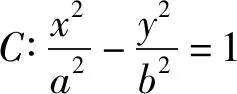
参考答案e=2.

评注以上三个题目均是直角背景下求双曲线的离心率问题，解法多样，但最简洁还是几何法，限于篇幅，请数学同仁自行探究，感悟其中的乐趣.

5 变式拓展

评注直角背景下的离心率问题很活，以上仅从直角顶点的位置在渐近线上、在曲线上、在坐标轴上进行了改装 ，问题就变得耳目一新.事实上还可变换曲线，将双曲线换成椭圆，这类问题也很受高考命题专家的青睐，有兴趣的同仁可以查阅历年高考题.

6 题型综述

直角背景下的离心率问题通常应从以下角度思考：圆锥曲线的第一定义式，正余弦定理，焦点三角形面积，三角换元，直线与直线的关系，直线与曲线的关系，向量的数量积，直线的斜率，互补角的诱导公式，互余角的诱导公式，相似形等，再辅以代数运算技巧，一般可以解决问题.其中最优解法是构造相似形的纯几何法，同时也是思维量最大的解法.多从几何角度思考研究此类问题有助于提高解题速度和正确率.