一类导数压轴题的解法

李昌成

(新疆乌鲁木齐市第八中学 830002)

1 发现问题

近期在研究全国各地模拟考试或统考题目发现，一类同时含有xex和lnx的求参数取值范围的函数题目，它们可以用分离参数构造函数等常规解法作答，但解答过程繁杂.仔细研究，这类题有其自身的结构特征，宜使用切线放缩法解答.

2 典例研究

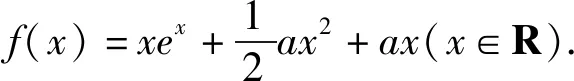
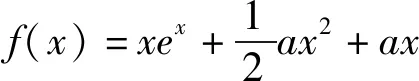
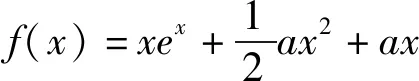
整理,得xex-3ax-lnx-1≥0.

令h(x)=xex-3ax-lnx-1，

则h(x)≥0恒成立.

因为xex=elnx·ex=ex+lnx，

所以h(x)=ex+lnx-3ax-lnx-1.

因为ex≥x+1，

所以h(x)≥(x+lnx+1)-3ax-lnx-1.

即h(x)≥x-3ax.

所以x-3ax≥0恒成立 .

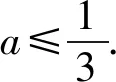
例2 (重庆市一中2022届高三上学期期中考试第16题)已知函数f(x)的导函数f′(x)满足f′(x)-f(x)=e2x，且f(0)=1，当x∈(0，+∞)时，x[f(x)-a]≥1+lnx恒成立，则实数a的取值范围是____.

分析由f′(x)-f(x)=e2x知f(x)=e2x，根据条件“x[f(x)-a]≥1+lnx”可以导出特征项“xe2x”，所以适合用切线放缩法解答.

解析因为(enx)′=nenx，

所以f′(x)-f(x)=e2x=2e2x-e2x.

由同构原理,得f(x)=e2x.

所以x[f(x)-a]=x(e2x-a)=xe2x-ax.

结合x[f(x)-a]≥1+lnx,得

xe2x-ax≥1+lnx.

因为xe2x=elnx·e2x=e2x+lnx，

所以e2x+lnx-ax-lnx-1≥0.

因为e2x+lnx≥2x+lnx+1，

所以(2x+lnx+1)-ax-lnx-1≥0.

即2x-ax≥0.

所以a≤2.

例3 (西南大学附属中学2022届高三第一学期期末考试理科第22题)对于任意的x∈(0,+∞)，lnx+2ax+1≤xe3x恒成立，求实数a的取值范围.

分析本题易于分离参数，然后利用xex=ex+lnx及ex≥x+1，放缩的同时构造新函数，可求得参数的取值范围.

解析由lnx+2ax+1≤xe3x，x∈(0,+∞)，

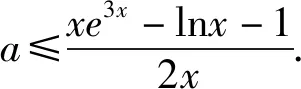
因为xe3x=elnx·e3x=e3x+lnx，

所以xe3x-lnx-1=e3x+lnx-lnx-1

≥(3x+lnx+1)-lnx-1

=3x.

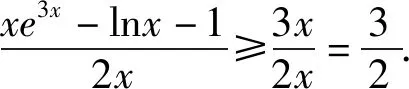
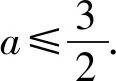
评析以上三例均含有(或变形得)xex和lnx+1，处理的办法雷同，恒等变形、放缩、求最值，套路明显.其本质特征是若xex和lnx+1在不等式的异侧，则xex的系数与lnx的真数的系数相反，当不具有这种特征时，解法失效.理由为：λxex=elnλx·ex=ex+lnλx≥x+lnλx+1，所以λxex-lnλx-1=λex+lnx-lnλx-1=λex+lnx才能整体消元.一般取λ=1.这样题目显得简洁明了，也不影响问题的本质.下面举一个形似质异的题目，以示区别.

例4(河南省洛阳市2022届高三第一次统一考试理科第12题)已知函数f(x)=xa-alnx(a>0)，g(x)=ex-x，若x∈(1,e2)时，f(x)≤g(x)成立，则实数a的最大值是( ).

分析表面上题设中也含有ex，lnx等，但不具有上述特征，需用其他办法解答.观察两函数的结构，非常相似，比较其差异可以发现alnx在f(x)中的“角色”与x在g(x)中“角色”一致，因此要在f(x)的函数形式上下功夫，结合对数恒等式是可以实现形式统一的.

解析因为x=elnx，

所以xa=(elnx)a=ealnx.

因此f(x)=ealnx-alnx=g(alnx).

因为f(x)≤g(x)，

所以g(alnx)≤g(x).

因为g′(x)=ex-1，

当x∈(1,e2)时，g′(x)=ex-1>0，

所以g(x)在(1,e2)上单调递增.

所以alnx≤x.

当x∈(1,e2)时，lnx>0，

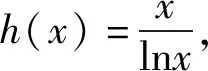
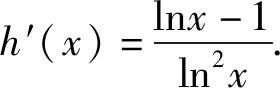
当x∈(1,e)时，h′(x)<0；

当x∈(e,e2)时，h′(x)>0.

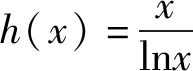
因此h(x)min=e.所以a≤e.故选A.

3 理论溯源

在人教A版(2005年版)普通高中课程标准实验教科书选修2-2第32页B组第1题的第3小题：证明ex>1+x(x≠0)，并通过函数图象直观验证结论.

事实上，本题通过图象可得函数f(x)=ex与h(x)=1+x恰好相切于点(0，1)，当x≠0时，f(x)的图象始终在h(x)的图象之上.俗称切线放缩.它的另一功能是实现了函数变换，减少或统一函数类型，方便于解题.

4 教学思考

4.1 教学应在公式的证明上下功夫

对于x=elnx，教材是没有提及的，甚至恒等式alogax=x也没有提到.这需要教师在教学中进行严格认真地证明，而不是直接告诉学生结果，直接刷题“硬”用.这样不仅应用别扭，而且容易遗忘.素不知，这是定义的抽象应用，等式左边是以logax为指数，a为底数的指数式，右端可以看作幂，依据对数的定义可得alogax=x⟺logax=logax，并且对x的范围也没有限制，所以此式叫恒等式.仅需将a换成e，等式x=elnx就成立了.在教学中，我们发现学生对此不熟悉，更谈不上灵活应用，对xex=ex+lnx就更加陌生了.所以我们应在公式证明上下功夫.

4.2 教学应在公式的理解上下功夫

对于ex≥1+x，我们应从形式和几何意义两方面进行深刻理解.这里的x可以换成任意的符号，均不影响不等式的正确性，例如en≥1+n将指数问题转换成数列了；esinx≥1+sinx将指数问题转换成三角函数了；elogax≥1+logax将指数问题转换成对数了.另外，从函数观点看，左端是曲线，右端是直线，并且二者具有相切关系，数形结合可以解决很多复杂的问题，尤其是与函数凸凹性相结合，是突破难题的一个杀手锏.例如2017年全国课标Ⅱ卷第21题：设函数f(x)=(1-x2)ex.

(1)讨论f(x)的单调性；

(2)当x≥0时，f(x)≤ax+1，求实数a的取值范围．

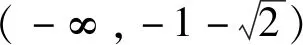
4.3 教学应在变式教学上下功夫