多元变量问题解题策略
2022-11-03黄少莹
黄少莹
(福建省莆田第二中学 351131)
多元变量函数问题是函数中的一大难点,问题类型多样,方法多变,但是解题思路主要把握一个宗旨“消参减元”,再辅以构造新函数进行解题.那么如何消参减元呢?本文主要就两大类型来探讨,一是x1,x2为定义域或所给区间中的任意两个变量;二是x1,x2为函数的零点、极值点或方程的两根.
1 利用同构式构造新函数以减元
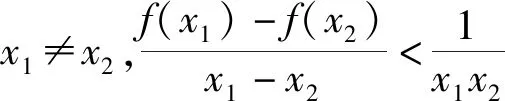
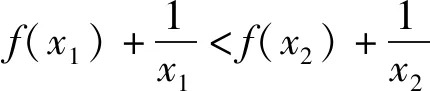
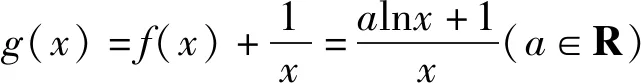
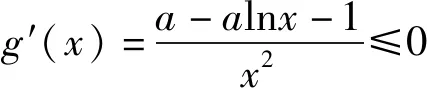
由于lnx∈[2,4],因此1-lnx<0.
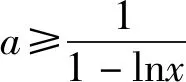
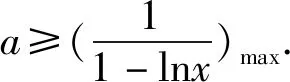
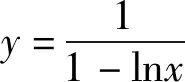
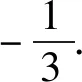
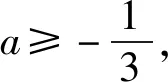
评析本题不等式中函数含有两个变量,此类问题的解题思路一般是将两个变量分离至不等式两边,利用同构式可将其转化为函数的单调性问题,构造新函数,利用导数达到“减元”的目的,最终再将问题转化为恒成立问题,通过函数的最值得到解决,考查了逻辑推理、数学建模及数学运算等核心素养.同时要特别注意此类问题在解决时要关注变量的取值范围,以及不等式是对该范围内的任意x1,x2恒成立.
例2(2020年天津卷20题)已知函数f(x)=x3+klnx(k∈R),f′(x)是f(x)的导函数.
(1)当k=6时,①求曲线y=f(x)在点(1,f(1))处的切线方程;

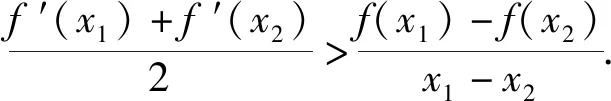
解析(1)①y=9x-8.

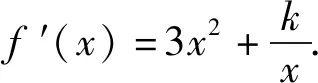
则对任意的x1,x2∈[1,+∞),且x1>x2,欲证
即证[f′(x1)+f′(x2)](x1-x2)>2[f(x1)-f(x2)]成立.
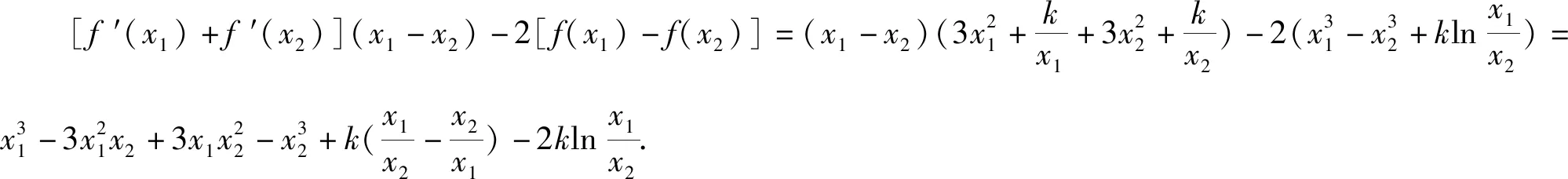

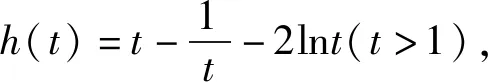
故h(t)在[1,+∞)上为单调递增.
所以h(t)>h(1)=0.
又因为k≥-3,

又x2>1,t>1,
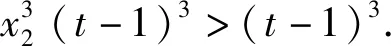

而由(1)②可得t>1时g(t)>g(1)=1.
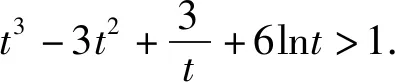
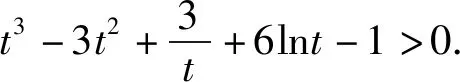
由此可得[f′(x1)+f′(x2)](x1-x2)-2[f(x1)-f(x2)]>0.
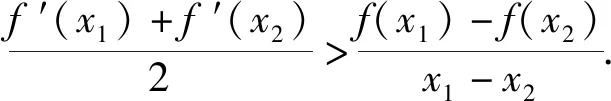
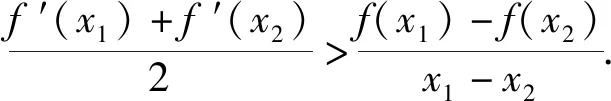
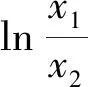

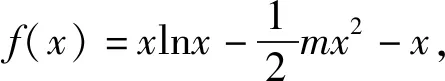
f′(x)=lnx-mx.
依题可得x1,x2为f′(x)=0的两个不等实根.
故lnx1-mx1=0,lnx2-mx2=0.
两式相加,得lnx1x2=m(x1+x2).
依此可得
故欲证x1x2>e2,即证lnx1x2>2.
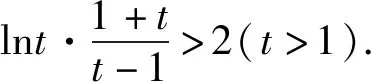

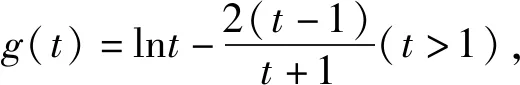
故g(t)在(1,+∞)上单调递增.
因此g(t)>g(1)=0.

即lnx1x2>2成立.
所以x1x2>e2.
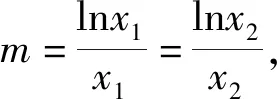
3 利用变量x1,x2的等量关系进行转化减元
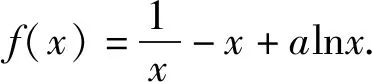
(1)讨论f(x)的单调性;
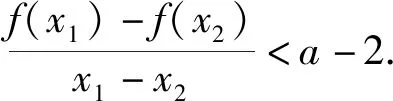
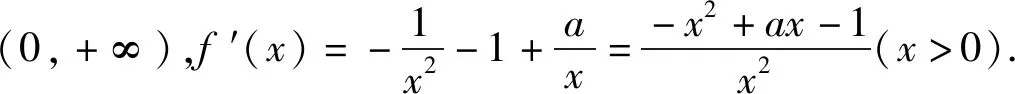
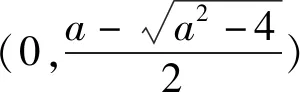
(2)由(1)可知若f(x)存在两个极值点x1,x2,则a>2,且x1,x2为-x2+ax-1=0的两根,即x1+x2=a,x1x2=1.
不妨设x1>x2,则x1>1>x2>0.
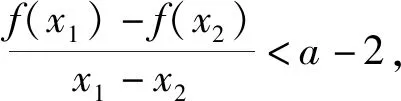
即证f(x1)-f(x2)<(a-2)(x1-x2).
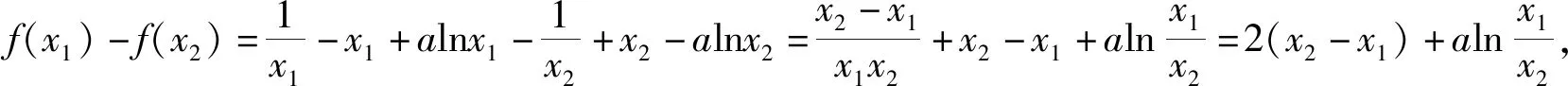

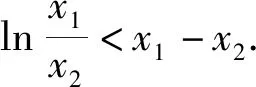
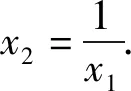

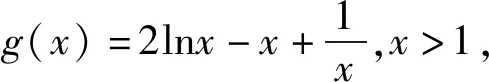
故g(x)在(1,+∞)上单调递减.
所以g(x) 例5(2016年新课标全国Ⅰ卷21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (1)求a的取值范围; (2)设x1,x2是f(x)的两个零点,证明:x1+x2<2. 解析(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a). ①设a=0,则f(x)=(x-2)ex,f(x)只有一个零点. ②设a>0,f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增. ③设a<0,由f′(x)=0得 x=1或x=ln(-2a). 故当x∈(1,+∞)时,f′(x)>0,因此f(x)在(1,+∞)上单调递增. 又当x≤1时,f(x)<0,所以f(x)不存在两个零点. 可得f(x)在(-∞,1)上单调递增,在(1,ln(-2a))上单调递减,在(ln(-2a),+∞)上单调递增.极小值f[ln(-2a)]<极大值f(1)=-e<0,所以f(x)不存在两个零点. 综上,a的取值范围为(0,+∞). (3)不妨设x1 又f(x)在(-∞,1)上单调递减, 所以欲证x1+x2<2, 即证f(x1)>f(2-x2). 而f(x1)=f(x2)=0,故只需证f(x2)-f(2-x2)>0,x2∈(1,+∞). 令g(x)=f(x)-f(2-x),x>1,则 g′(x)=f′(x)+f′(2-x) =(x-1)(ex+2a)+(1-x)(e2-x+2a) =(x-1)(ex-e2-x) 又x>1,故g′(x)>0. 因此g(x)在(1,+∞)上单调递增. 故g(x)>g(1)=0. 从而有x2∈(1,+∞)时f(x2)-f(2-x2)>0. 故x1+x2<2得证. 评析第(1)问主要是为第(2)步作铺垫得到f(x)的单调性,需由此先得到x1,x2的大致范围,再根据所证不等式中x1,x2的和(积)形式转化发现x1,2-x2在同一单调区间,因此考虑将所证问题转化为证明f(x1),f(2-x2)间的大小关系,又利用f(x1)=f(x2),将问题再次转化为f(x2),f(2-x2)间的大小关系,从而构造函数g(x)=f(x)-f(2-x),x>1,证明g(x)>0即可.这种解法中不管所证不等式是x1,x2的和还是积都可将x1,x2分离至不等式两边,并保证它们在已知函数的同一单调区间内,然后利用函数单调性的定义将单调性与a,b大小、f(a),f(b)大小综合起来,从而将问题进行等价转化,结合f(x1)=f(x2)将变量统一为x1或x2,从而构造出新函数以解题.比如例4也可用这种方法解决,读者可自行动手试试. (1)求a的取值范围; 教学中我们不应仅仅是教会学生“这道题”怎么做,更重要的是要引导学生学会对题目条件进行深入挖掘,根据不同条件特征、问题结论等进行方法的选择,当条件特征、问题结论与常见(已掌握)的形式不同时,又应如何转化,如何在解题中真正做到消参减元.在教导通性通法的同时,还应抓住题目条件所包含的信息、知识点与证明结论的转化间的异同及关联,引导学生学会归纳总结其中条件的不同、问题结论的不同与对应方法间的联系,以真正领悟各类方法的数学本质,这样才能真正做到“会一题,通一类”.而这正是对高考评价体系中学科素养所包括的“学习掌握、实践探索、思维方法”3个一级指标的最好践行.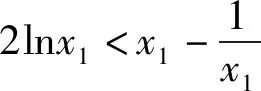
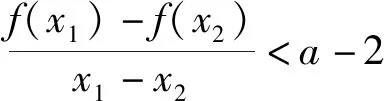
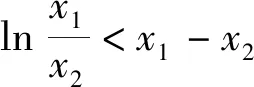
4 对称变换回归同一单调区间
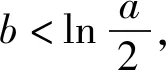
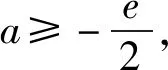
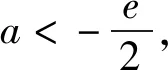
5 类题训练